Повышение статической и динамической точности управления механизмом параллельной структуры космического назначения

Современные космические аппараты (КА) применяются в широком спектре информационных систем для решения таких прикладных задач, как обеспечение телевещания, интернета, спутниковой связи, мониторинга поверхности Земли, а также передовых исследований космического пространства – реликтового излучения, черных дыр, галактик и др. [1–3].

Для достижения высокой точности работы информационных систем КА необходимо с максимальной точностью ориентировать их бортовые приборы (антенны и контррефлекторы, телескопы и др.). В современных КА требования к точности

линейного позиционирования и угловой ориентации имеют порядок микрометров и микрорадиан соответственно [4].

Зачастую такие системы позиционирования и ориентации строятся на основе прецизионных механизмов параллельной структуры (МПС) [5–7], рассчитанных на длительную эксплуатацию в экстремальных условиях внешней среды: вакуум, воздействие ионизирующего излучения, широкий диапазон температур.

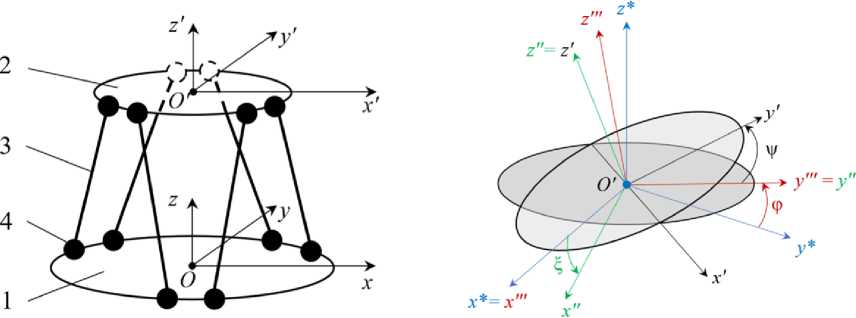
В БГТУ «ВОЕНМЕХ» им. Д. Ф. Устинова совместно с АО «РЕШЕТНЁВ» разработан МПС типа гексапода, кинематическая схема которого приведена на рис. 1. В гексаподе неподвижное основание (1) соединяется с платформой (2) с помощью шести линейных приводов (3) через шарниры (4). Перемещение верхней платформы (система координат O'x'y'z' ) относительно нижней ( Oxyz )

происходит во всех шести степенях свободы при изменении длин линейных приводов.

Для задания положения платформы относительно основания введем декартовы координаты X , Y , Z (положение O' в системе Oxyz ), а для ее ориентации - углы Эйлера, как показано на рис. 1 б) .

Отметим, что для принятой системы углов сначала осуществляется поворот на угол ф отно сительно оси x* и переход к системе координат O'x"'у"'z"', затем - поворот на ^ вокруг у"' и переход к O'x"у"z" и, наконец, - поворот на у вокруг z" и переход к системе координат верхней платформы O'x'у'z'. При этом, в зависимости от конкретного назначения наводимого объекта, можно использовать другой способ задания углов Эйлера, например, повороты относительно осей абсолютной системы координат O'x *у *z *.

аб

Рис. 1. Схема гексапода ( а ) и расположение его углов Эйлера ( б )

Таким образом, положение подвижной платформы в пространстве описывается вектором:

q = [ X , Y , Z , φ, ξ, ψ] ^T, а управление гексаподом сводится к нахождению вектора L = [ L ₁, ..., L ₆] ^T , содержащего длины всех линейных приводов.

При управлении гексаподом чаще всего решаются две задачи кинематики [4; 8; 9]: обратная, то есть нахождение длин приводов L по координатам верхней платформы q , и прямая - определение q по L .

Решение задач кинематики базируется на преобразовании однородных координат платфор- мы и основания: r = Thr', где r = [X, Y, Z, 1]T - вектор координат некой точки в неподвижной системе Oxyz (рис. 1 а), r' - аналогичный вектор этой же точки, но в подвижной системе координат Oʹxʹyʹzʹ.

При этом матрица:

Т =

T h =

^R p ^p 0001

где p = [ X , Y , Z ] ^T – координаты в системе основания Oxyz центра системы платформы O'x'y'z' , R p - матрица поворота, которая при использовании углов Эйлера, как показано на рис. 1 б , равна:

R p

cos ^cos у                — cos^sin у            sin^

cos фsin у + cos у sin ^sin ф cos у cos ф- sin^sin у sin ф - cos^sin ф sin у sin ф- cos у cos фsin £ cos у sin ф + cos фsin^sin у cos^cos ф

Отметим, что кинематическая схема гексапода может строиться на основе приводов и шарниров с различным количеством степеней свободы.

Длину i -го привода гексапода можно найти с помощью выражения L , = 11 r . - T_Ar^ . 11, где T h - матрица преобразования, вычисленная по приведенным выше уравнениям для заданного вектором q = [ X , Y , Z , ф, ^, у] T положения подвижной платформы гексапода; r_А.- вектор однородных координат в системе Oxyz шарнира основания A i , r^.- вектор однородных координат в системе O'x'y'z' шарнира платформы B_i .

Находя таким образом длину каждого привода гексапода, можем решить обратную задачу его кинематики.

В свою очередь, прямая задача кинематики для подобных механизмов не имеет единственного аналитического решения [10]. Так, для платформы Гью-Стюарта возможно существование до 40 таких решений, обусловленных в некоторых случаях количеством конфигураций сборки МПС с заданными длинами приводов.

Учитывая это обстоятельство, в рассматриваемом гексаподе прямая задача кинематики гек-

сапода решается преимущественно численными методами. При этом чтобы избежать сингулярности, во время численных расчетов вместо углов Эйлера применяются кватернионы [4].

При прецизионном управлении полезной нагрузкой основным требованием является обеспечение высокой статической (квазистатической при движении с малыми скоростями) и динамической точности угловой ориентации и линейного позиционирования объектов.

• 1.    Повышение статической 118 и квазистатической точностигексапода

Для построения качественной системы управления МПС необходимо применение обратной связи по координатам платформы q . Однако экстремальные условия внешней среды делают ее реализацию практически невозможной из-за существенных ограничений на применяемую компонентную базу [11].

При реализации разомкнутой системы управления на точность наведения и позиционирования аппаратуры, закрепленной на подвижной платформе, будут влиять такие источники ошибок, как погрешности изготовления и сборки механической части, температурные расширения деталей, а также точность учета данных ошибок и параметров кинематики в программном обеспечении. При этом большая часть этих ошибок связана с линейными приводами МПС.

Таким образом, для повышения точности наведения, учитывая практические сложности при построении системы измерения координат подвижной платформы космического применения [12], а также для построения модульной конструкции рассматриваемого механизма, наиболее оптимальным является обеспечение функционирования линейных приводов как замкнутых исполнительных устройств или сервоприводов со встроенными датчиками линейного положения.

Накладываемые ввиду экстремальных условий эксплуатации ограничения на используемую компонентную базу значительно усложняют построение замкнутого по перемещению линейного привода, поэтому авторами было предложено [12; 13] использовать косвенную обратную связь по углу поворота в шарико-винтовой передаче (ШВП) с ее индивидуальной калибровкой и алгоритмом программной компенсации линейного теплового изменения размеров элементов гексапода.

Авторами было показано, что построение такого линейного привода требует ряд мероприятий для увеличения точности его работы. Так, необходимо обеспечить предварительный натяг в ШВП, высококачественную сборку, настройку датчиков нулевого положения. Также требуется

Том 7

соблюдать допустимые режимы работы в части механических нагрузок, температурного диапазона и параметров движения, в том числе для того, чтобы не нарушать режимы смазывания.

При этом дополнительно вводится программная компенсация основных ошибок линейного привода, к которым относятся:

• •    систематические ошибки: погрешности ШВП, редуктора, обмоток двигателя и др.;

• •    температурные ошибки из-за изменения размеров деталей, вызванного нагревом или охлаждением;

• •    ошибки, вызванные упругими деформациями МПС под действием нагрузки.

• 2.    Повышение динамической точности гексапода

Систематические ошибки можно компенсировать с помощью предварительной калибровки каждого линейного привода, температурные - путем размещения соответствующих датчиков и введения поправок в алгоритмы управления. Уменьшить влияние упругих деформаций при движении платформы МПС космического применения можно как путем снижения динамических нагрузок (работа в квазистатическом режиме), так и путем введения специального наблюдателя состояния в части линейной нагрузки на каждый привод и последующей программной компенсации упругой деформации [12; 13].

Применение указанных методов позволяет повысить в несколько раз статическую и квази-статическую точность механизма параллельной структуры, а также получить более дешевую и надежную систему наведения и ориентации различных приборов для космических аппаратов.

К механизмам параллельной структуры предъявляются жесткие требования не только в части показателей качества в статическом режиме (точность позиционирования), но и в динамическом режиме. Так, при управлении крупногабаритной конструкцией МПС должен минимизировать длительность переходных процессов позиционирования и наведения объекта и оказывать минимальные динамические возмущения как на объект управления, так и на КА, на котором закреплен МПС.

Достичь этого можно введением ограничений на развиваемые скорости, ускорения, и другие производные положения подвижной платформы МПС. Это позволяет как защитить оборудование и КА от чрезмерных динамических нагрузок, так и ограничить мощность, потребляемую МПС.

Для реализации управления МПС с динамическими ограничениями необходимо применять специальные алгоритмы планирования траектории движения верхней платформы. При этом управление МПС может осуществляться в различных режимах:

• •    контурное управление - платформа движется от начальной к конечной точке по непрерывному, жестко заданному пути;

• •    траекторное управление - платформа движется от начальной к конечной точке по непрерывному пути с прохождением заданных промежуточных точек (узлов);

• •    позиционное управление - платформа движется от начальной к конечной точке по произвольной траектории.

Планирование пути между заданными начальной, конечной и (при наличии) узловыми точками может быть реализовано различными методами интерполяции траектории [13]. При этом для многозвенных механизмов такая задача может решаться как на устройстве верхнего уровня, реализующем управление выходной координатой всего устройства [14-16], так и на устройствах нижнего уровня, управляющих отдельными приводами.

Преимуществом реализации траектории системой управления нижнего уровня (непосредственно привода) является более простой контроль развиваемых им скоростей, ускорений и рывков (скоростей ускорений), так как в реальных системах помимо заданных ограничений динамического воздействия на полезную нагрузку и несущую платформу, есть еще физические ограничения возможностей приводов (например, ограниченные возможностями электродвигателя и источника питания скорость и развиваемый момент).

Однако, при такой реализации планирования траектории практически невозможно добиться движения верхней платформы гексапода по заданному пути, а также довольно трудно пересчитывать ограничения по динамике, накладываемые на платформу к ограничениям на приводах [17].

В свою очередь, реализация алгоритма планирования траектории на устройстве верхнего уровня (в координатах платформы) позволяет ограничивать такие динамические возмущения напрямую для объекта управления, а также обеспечивать движение платформы по заданному пути.

Для позиционного режима такое управление обычно реализуется разбиением пути на участки, которые интерполируются полиномами различных степеней. Так, часто используемая траектория типа 4-3-4 включает три участка, описываемые полиномами четвертой, третьей и четвертой степеней соответственно [16]. При этом рассчитать коэффициенты полиномов 4-3-4 напрямую, исходя из заданных ограничений на скорости, ускорения и рывки платформы, затруднительно. Для ограничения динамики движения объекта целесообразно использовать траекторию движения 3-2-3-1-3-2-3. Входными данными алгоритма расчета ее коэффи- циентов, предложенного в [14], являются указанные ограничения напрямую.

Отметим, что на практике применить алгоритм планирования траектории 3-2-3-1-3-2-3 напрямую для обобщенных координат длин приводов L не получается, так как после решения обратной задачи кинематики траектории приводов будут иметь производные более высоких порядков, чем траектория платформы гексапода. При этом получение первой и последующих производных L требует проведения многократного численного дифференцирования, при котором погрешность значительно возрастает вместе с порядком производных.

Известно, что для уменьшения как статических, так и динамических ошибок управления многосвязными объектами можно применить алгоритмы управления, обеспечивающие учет и компенсацию влияния динамических эффектов на основе решения обратной задачи динамики механизма. Так, динамика гексапода может быть описана уравнением Лагранжа второго рода:

т = M(q)q + N(q, q) + G(q), где т - вектор усилий и моментов в пространстве декартовых координат; M(q) - матрица инерции гексапода; N(q, q) - матрица кориолисовых и центробежных усилий и моментов; G(q) - матрица гравитационных сил.

При управлении с компенсацией составляющих τ можно уменьшить влияние нелинейных и нестационарных элементов матриц M , N и G , и, тем самым, уменьшить ошибки управления, задаваемые разностями реальных координат платформы q , q , q и задаваемых величин q _з , q _з , q _з .

На рис. 2 приведен пример реализации такой системы управления гексаподом, использующей решение прямой задачи кинематики (ПЗК) и обратной задачи динамики (ОЗД) [8]. Здесь J - матрица Якоби гексапода, F = ( J T ) (т_т + т ₂) - вектор сил в линейных приводах гексапода, где т 1 формируется ПД-регулятором с матрицами коэффициентов К _П и К _Д, а т ₂ = M ( q ) q _з + N ( q , q ) + G ( q ) - рассчитываемый с помощью ОЗД компенсационный вектор.

Отметим, что, несмотря на все имеющиеся преимущества, практическая реализация такой системы управления затруднительна. В первую очередь, необходимо знать точные параметры матриц J , M , N и G , характеризующие массо-инерционные и упруго-демпфирующие свойства конкретного гексапода. При этом нахождение этих матриц на каждом такте управления требует значительных вычислительных мощностей.

Рассмотрим силы, возникающие в линейном приводе гексапода при сложном гармоническом движении подвижной платформы по всем шести

(шмчесЬё

АППАРАТЫ И

Том 7

степеням свободы одновременно в квазистатиче- скоростях по каждой координате. На рис. 3–5 при-ском режиме, а также при увеличенных в 20 и 60 раз ведены графики составляющих этих усилий.

Гексапод

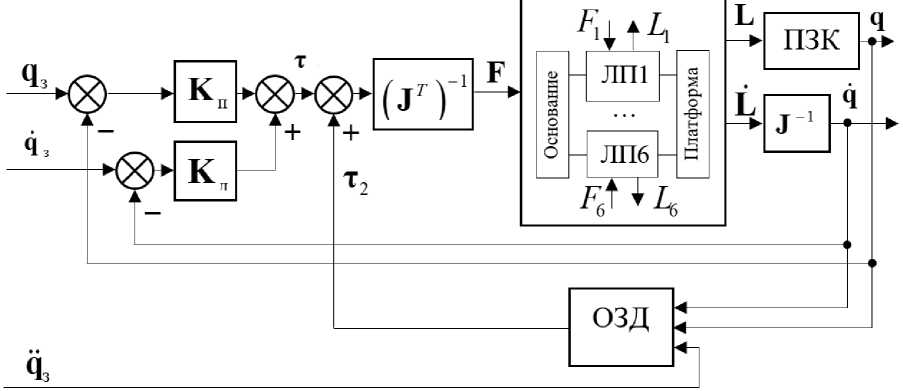
Рис. 2. Система управления гексапода с решением ПЗК и ОЗД

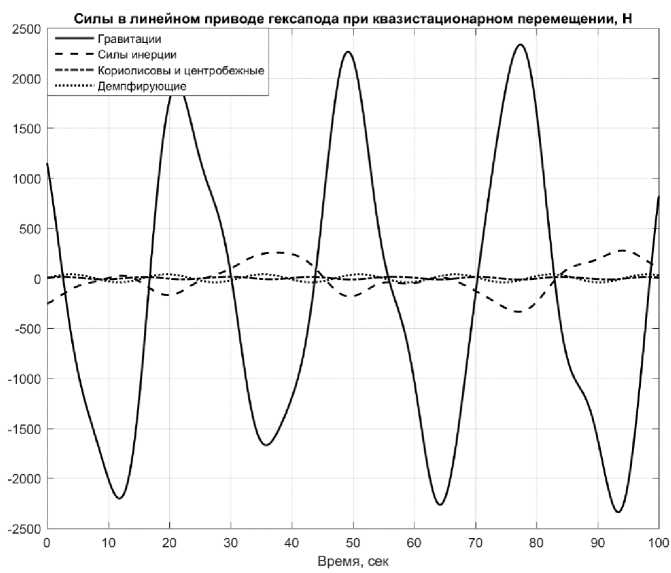
Рис. 3. Силы, возникающие в линейном приводе при квазистатическом режиме работы гексапода

Из рисунков видно, что помимо гравитационных сил, которые не зависят от скоростей движения и практически не проявляются при работе МПС в условиях микрогравитации, основной вклад в суммарное усилие нагрузки привода вносят силы инерции.

Учитывая вышесказанное, а также сложность построения системы управления, компенсирую- щей динамику движения механизмов параллельной структуры (рис. 2) и условия функционирования рассматриваемого гексапода (квазистатиче-ский режим в невесомости), рассмотрим вариант построения системы управления в пространстве обобщенных координат платформы механизма параллельной структуры (длин приводов), приведенный на рис. 6.

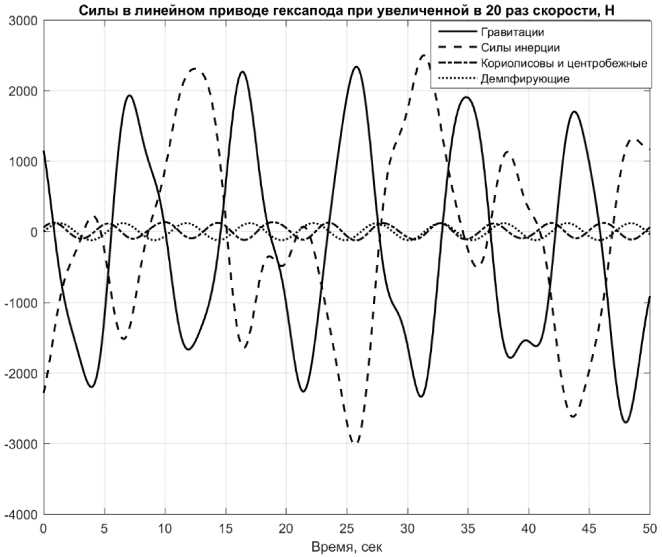
Рис. 4. Силы, возникающие в линейном приводе гексапода при увеличенных в 20 раз скоростях движения платформы

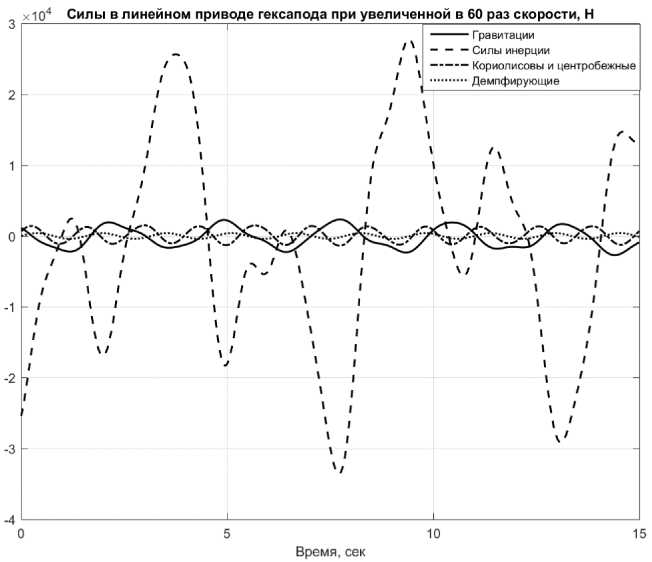
Рис. 5. Силы, возникающие в линейном приводе гексапода при увеличенных в 60 раз скоростях движения платформы

Система на рис. 6 работает следующим образом. На этапе подготовки к движению МПС (объекта управления) выполняется по алгоритму [14] расчет траектории для заданного вектора конечного поло жения платформы qз = [Xз, Y3 , Zз, фз, §3 , у з ] с учетом ограничений q3, qз , q3. Результатом это расчета для цифровой системы управления является вектор:

q3 (kT) = [Х3 (kT),уз (kT),zз (kT),аз (kT),P3 (kT),y (kT)], где k = 1, 32 - номер такта системы управления, T - период ее дискретизации.

Путем решения обратной задачи кинематики механизмов параллельной структуры полученный набор данных ( q ₃ ( Т ),... , q ₃ ( nt )} пересчитывается в набор задаваемых длин линейных приводов ( q ₃ (Т ),..., q ₃( nt )^, которые в режиме реального времени передаются на соответствующие системы управ л е н ия нижнего уровня. Реализуя ограничения q ₃ , q ₃ , q ₃ таким образом, чтобы гексапод функционировал в квазистатическом режиме, и учитывая практически полное отсутствие сил гравитации, можем предположить, что основные статические и динамические ошибки такого дви- ¹²² жения будут определяться только квазистатиче-скими ошибками линейных приводов.

Отметим, что на практике при физических ограничениях интерфейсов связи в части скорости передачи данных и соответствующем увеличении периода дискретизации T , возможно применять дополнительную внутрипериодную интерполяцию значений, принимаемых системой управления привода. Управление электродвигателем такого следящего привода может быть реализовано в векторном режиме с помощью датчика угла (например, вращающийся трансформатор) и датчиков тока (шунтов), что позволяет улучшить его динамические характеристики, регулируя момент и потокосцепление ротора [13].

Том 7

Заключение

Для прецизионного управления МПС, предназначенного для функционирования в экстремальных условиях космического пространства, требуется построение замкнутой по положению подвижной платформы системы управления. При этом из-за практической невозможности применения датчиков такую обратную связь следует реализовывать косвенным методом по углу поворота вала исполнительного двигателя линейного привода. При этом, для обеспечения высокой точности работы МПС такая система требует применения различных решений для компенсации ошибок. Так, для повышения статической точности МПС необходим предварительный натяг шарико-винтовой передачи и другие конструктивные решения, при этом погрешность изготовления передачи и ее температурное расширение можно компенсировать программно.

Для повышения динамической точности управления необходимо применение траекторного управления с ограничениями максимальных рывков, ускорений и скоростей движения платформы гексапода. При этом формировать траекторию движения МПС следует в координатах платформы, далее пересчитывать в обобщенные координаты (длины линейных приводов) и отрабатывать их в следящем режиме.