Повышение точность работы робота за счет применения нейронных сети (нейронных компенсаторов и нелинейной динамики)
Автор: Чжэнцзе Янь, Клочков Ю.С., Лин Си
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 4 т.24, 2022 года.
Бесплатный доступ
Предметом данной статьи является программируемая система управления роботом-манипулятором. Рассмотрена сложная нелинейная динамика, связанная с практическим применением систем и манипуляторов. Традиционный метод управления заменяется разработанной системой Elma и адаптивной радиальной базовой функцией нейронной сети, что повышает стабильность системы и скорость отклика. С помощью программного обеспечения, связанного с MATLAB, разработаны соответствующие контроллеры и компенсаторы. Представлены результаты обучения нейросетевого контроллера для программирования траекторий робота. Анализируются динамические ошибки различных типов нейросетевых контроллеров и двух методов управления.
Робот-манипулятор, программируемая система управления, нейронная сеть, нелинейные многомерные компенсаторы, моделирование, динамический анализ, динамические ошибки
Короткий адрес: https://sciup.org/148325297
IDR: 148325297 | УДК: 62-529 | DOI: 10.37313/1990-5378-2022-24-4-106-115
Текст научной статьи Повышение точность работы робота за счет применения нейронных сети (нейронных компенсаторов и нелинейной динамики)
На раннем этапе проектирования управления манипулятором динамическая модель системы и связанные с ней параметры системы должны быть точно описаны при проектировании контроллера [1]. В традиционных методах проектирования управления, таких, как вычислительное управление крутящим моментом и управление обратной динамикой, это работает нормально [2]. Рассчитав крутящий момент манипулятора робота и составив динамическое уравнение, вы можете получить хороший эффект управления [3]. Но данные методы основаны на возможности получить точную модель данных. Однако получить точную математическую модель робота в реальном производстве и использовании сложно [4]. Кроме того, из-за влияния различных полезных нагрузок могут возникнуть трудности с получением соответствующих методов на основе моделей. В последнее время нейросетевые калькуляторы используются для улучшения характеристик систем управления при разработке систем управления роботами-манипуляторами. В системах числового управления (ЧПУ) нейросетевой интерполятор траекторий звеньев робота может использоваться вместо традиционного сплайн-интерполятора [5].
Это исследование используется для обучения компенсаторов с использованием нейронных сетей в системах числового управления роботами-манипуляторами и при отсутствии точных исходных данных [6]. Адаптивный нейросетевой компенсатор используется для замены традиционного ПИД-регулятора и других методов компенсации динамической ошибки, вызванной скручивающей нагрузкой в приводе звена робота [7]. Нелинейная динамическая связь привода выбирает двухпрямой робот-манипулятор в угловой системе координат в качестве моделируемого объекта управления [8].
Целью данной работы является синтез и обучение многомерного нейросетевого контроллера для компенсации и коррекции динамической ошибки траектории робота. И контроллер нейронной сети, и моделирование проекта выполняются в MATLAB [9].
-
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ НЕЛИНЕЙНЫХ ДИНАМИЧЕСКИХ КОМПЕНСАТОРОВ
Как правило, многомерные компенсаторы динамических ошибок описываются нелинейными выражениями, соответствующими динамической модели робота, представленной в виде уравнений Лагранжа:
где (q, q', q) - N x 1 векторов обобщенных координат положений, скоростей и ускорений звеньев робота; N – количество ссылок робота.
Основными нагрузками приводов робота являются элементы векторов левой части в уравнении (1), где:
Q_iner = A (q) q ̈ - N × 1 вектор моментов инерции или сил, вызванных ускоренным движением звеньев; A (q) - матрица кинетической энергии N × N механизма робота;
Q_cor = B (q, q ̇ ) q ̇ - вектор N × 1 кориолисовых и центробежных моментов или сил; B (q, q ̇ ) - матрица N × N;
Q_grav = C (q) - N × 1 вектор гравитационных и других потенциальных моментов или сил.
В правой части уравнения (1): Q_d – вектор N × 1 крутящих моментов или сил, создаваемых приводами робота; Q_L – вектор N × 1 дополнительных нагрузок, возникающих в приводах из-за трения в соединениях и действия внешних сил на захват.
Траектории звеньев робота в системах ЧПУ рассчитываются путем решения обратных задач кинематики в базовых точках траектории захвата робота, а затем они интерполируются с использованием полиномов сплайнов. Следовательно, используя программные значения векторов положения, скорости и ускорения звеньев (q_p, (q_p) ̇, (q_p) ̈ ), можно рассчитать программные значения крутящего момента или силовых нагрузок, которые приводы звена должны преодолеть:
; ; ; (2) ;;
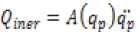
Qff =<2mer + Qcor + Qgrav (3)
Выражения (2) и (3) могут быть непосредственно использованы для компенсации динамических ошибок в системах ЧПУ роботов с моментными приводами звеньев и ПИД-регуляторами положений звеньев робота (Игнатова и Ростов, 2014). На рисунке 1 показана соответствующая функциональная схема системы с динамическими компенсаторами, включенными в схему прямой связи (FF) системы управления.
Однако, если есть дополнительные нагрузки Q_L, система с контролем крутящего момента FF может иметь большие динамические ошибки, которые могут быть уменьшены с помощью дополнительного линейного компенсатора:
upid = Kpe + K^ edt — K4q + Kcomq‘p , (4) где K_com = diag {K_ (com, i)} – матрица коэффициентов линейного компенсатора.
Нелинейные компенсаторы могут быть включены в обратную связь (FB) системы управления вместе с ПИД-регулятором или более сложным нелинейным регулятором. В этом случае компенсаторы FB используют сигналы обратной связи реальных положений и скоростей звеньев робота, измеренных соответствующими датчиками:
Qiner = ^^^pid^cor = B(q,q)q ; Qgrav = Clq>. (5) ;
Qfb = ^iner + Qcor + ^arav, (6) где вектор Upid рассматривается как вектор реальных ускорений.
На рисунке 2 показана функциональная схема с нелинейными компенсаторами FB, включенными в замкнутый контур системы.
Многовариантные компенсаторы (5) и (6) выполняют линеаризацию нелинейной динамики робота, описываемой уравнением (1), и тем самым обеспечивают более стабильную работу приводов робота.
-
3. ОБУЧЕНИЕ НЕЛИНЕЙНЫХ НЕЙРОСЕТЕВЫХ КОМПЕНСАТОРОВ
-
3.1. Проектирование компенсаторов с помощью нейронных сетей Элмана
-
Цель исследования заключалась в разработке модели адаптивной нейронной схемы управления нелинейными динамическими системами манипуляционного робота.
В качестве примера рассмотрим промышленный трехзвенный робот-манипулятор, звенья которого соединены между собой приводами вращательного движения. Положение звеньев определяется углами ϕ 1 , ϕ 2 , ϕ 2 . Помимо этого, на звенья робота действуют силы веса, которые направлены под некоторым углом α к выбранной системе координат, что демонстрирует возможность устройства работать под любым углом к горизонту.
Основной характеристикой объекта управления является его передаточная функция, записанная в терминах преобразования Лапласа, которая определяет соотношение выхода объекта y(s) к входу x(s) при нулевых начальных условиях.
Математическая модель, описывающая движение робота, имеет следующий вид:
ф = O)y (Oy = -^7 (Oy + ^ 5, ( 7 )
где Ф – угол отклонения от заданной траектории движения;
tOy – угловая скорость вращения вокруг вертикальной оси;
-
5 – угол поворота вокруг вертикальной оси;
T s – постоянная времени;
K – постоянный коэффициент с размерностью рад/с.
Уравнение, описывающее объект управления, имеет характер интегрируемого звена с опозданием, и описывается дифференциальным уравнением, поскольку в качестве исходной величины рассматривается не угловая скорость, а угол поворота, который является интегралом от угловой скорости:
T^ + d^ = kXi (8)
dt1 dt *■
Передаточная функция звена:
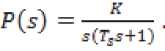
Привод робота имеет характер апериодического звена первого порядка, который можно описать дифференциальным уравнением:
T dx* + X, = kxr(10)
dt ‘
Соответственно передаточная функция звена привода имеет следующий вид:
я (5) =(11)
-
4 " Тгз+1
Для управления движением робота-манипулятора, представляющего собой нелинейную динамическую систему, целесообразно применять нейроконтроллер, который базируется на искусственной нейронной сети Элмана (рис. 1):
аЧЛ) = tansig (IW^p + ЛИ^раЧк — 1) + Ь1) ;
.
Преимуществом нейронной сети Элмана является повышенная устойчивость, поскольку в ней обратные связи заведены из выходов внутренних нейронов на промежуточный слой, что делает ее более устойчивой по сравнению с рекуррентной сетью аналогичного типа (например, нейронная сеть Хопфилда, в которой внутренние обратные связи подводятся к первичным входам, где происходит смешивание сигналов). Кроме того, нейронная сеть Элмана позволяет учитывать предысторию наблюдаемых процессов и накапливать информацию для выбора правильной стратегии управления роботом.
В системе MatLab / Simulink создана модель искусственной нейронной сети для управления манипуляционным роботом, содержащая входной слой из 15 нейронов и скрытый слой в вариантах от 12 до 19 нейронов, которые имеют локальные обратные связи через линии задержки. Выходной слой содержит 1 нейрон с линейной функцией активации (purelin) (см. рис. 2).
Состояние нейронов рекуррентного слоя сети опишем следующими уравнениями: (V (к) = LWVCk -1) + wup + Ь^аЧо) = aj оЧк) = t™sifl(n4k)). (12)
Линейный слой нейронной сети является безынерционным, а состояние его нейронов определяется соотношениями:
I fn2 (к) = LW^a1^) + b2
а2 (к) = purelin(n2 (к)).
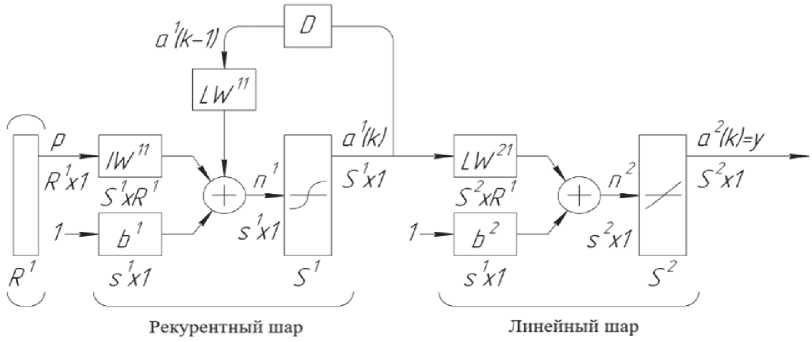
Рис. 1. Структура нейронной сети
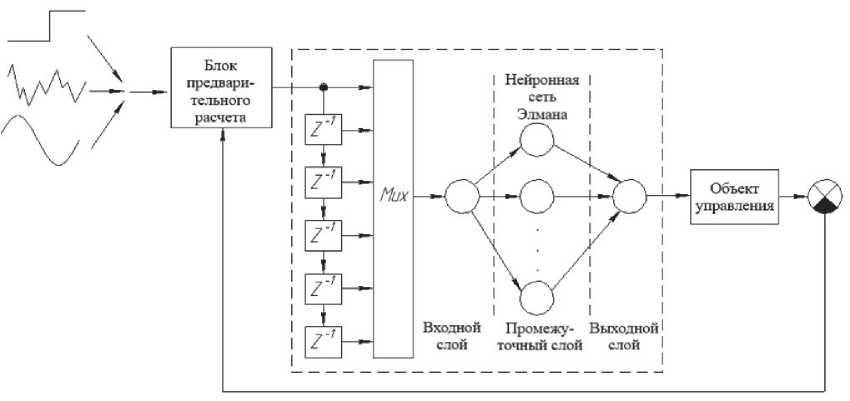
Рис. 2. Структурная модель искусственной нейронной сети управления промышленным трехзвенным манипуляционным роботом
Последовательность значений выходного сигнала, который попадает на линию обратной связи с задержкой, содержащей N-1 блоков опоздания z-1, а выход линии задержки, который состоит из значений входа в момент времени k, k-1, ..., k-N-1, опишем следующим выражением:
Угол поворота манипулятора представим в виде общей переменной , где u1 - настоящий угол поворота первого звена и u2 - настоящий угол поворота второго звена. Поскольку в этом примере , поэтому удовлетворяются равенства z = (z±,z2) = It и где r1 и r2 – желаемые углы поворота манипулятора; z – управляемая траектория манипулятора, v – дополнительная траектория манипулятора, y – вектор состояния манипулятора.
Для описания изменений желаемых углов поворота манипулятора используем следующие законы: r1(t) = sin(t) и r2(t) = cos(t).
Опишем модель нейронной схемы адаптивного управления манипулятором с помощью такого уравнения состояний с переменной структурой:
(—a — |vL если u > v; u = — = —(a + |v|)syn(u — v) = j 0, если и = v;
\ a + |i?|, если u < v.
(16) где – вектор состояний, – посто янный параметр,
( 1, если it > v;
1—1, если и < v.
Для получения решений представленного уравнения численным методом используем соответствующие два разностных уравнения с шагами по времени . Элементы функции в этих уравнениях вычисляют как конечные разности первого порядка (разностные коэффициенты Ньютона). В указанных уравнениях равенство u = r заменяется на неравенство .
Обучение сети (корректировку весовых коэффициентов и смещений нейронов до достижения заданной ошибки) будем проводить с использованием метода сопряженных градиентов (Флетчера-Ривса), которому свойственна хорошая сходимость вычислительного процесса: для положительно определенной квадратичной функции от n переменных минимум достигается не более чем через n шагов.
Алгоритм обучения нейронной сети состоит из следующих шагов:
-
1. В начальный момент времени t=1 все нейроны скрытого слоя устанавливаются в нулевое положение - исходное значение равно нулю.
-
2. Входное значение подается на сеть, где происходит его прямое распространение.
-
3. Согласно выбранному алгоритму Флетчера-Ривса, который по сравнению с алгоритмом градиентного спуска, регулирует скорость сходимости не только за счет настройки параметра скорости, но и корректирует размер шага на каждой итерации, достижение установленного значения ошибки выполним за минимальное количество итераций.
-
4. Установим t=t+1 и осуществим переход на 2 шаг. Обучение нейронной сети выполняется до тех пор, пока суммарная среднеквадратичная погрешность сети не примет наименьшее значение.
-
3.2. Проектирование компенсатора с адаптивной радиальной базовой функцией нейронной сети для аппроксимации локальной модели
В этой части разрабатывается компенсатор нелинейной динамической модели на основе нейронной сети RBF на основе литературы (2) и (3), который сравнивается с компенсатором нейронной сети в предыдущей части.
где — матрица момента инерции порядка n*n, _ ^ '' " — вектор центробежной силы порядка n*n, — вектор силы тяжести порядка n*1, q — вектор, представляющий переменную сустава, а τ — вектор приложенного крутящего момента в суставе.
Динамическое уравнение манипулятора обладает следующими свойствами
Свойство 1. Матрица инерции является симметричной положительно определенной;
Свойство 2. Если ^xCq-q) определяется правилом записи Кристоффеля, матрица ^х(ч) — 2Cx(q,q) кососимметрична.
Поскольку и являются просто функциями q, их можно моделировать с помощью статических нейронных сетей.
m„tJ(q) -Ej »jtj!4jj(v) +^/») = ^/fcjW+ Emk/'?):
Sxk(q)
= Ei
Pki^M^ + £kk + £м№
Среди них — веса нейронной сети; — радиальная базисная функция, входом которой является вектор q, — ошибки моделирования mxkj(q) и соответственно и считаются ограниченными.
Для моделирование с помощью динамической нейронной сети с входными данными q и q. Модель нейронной сети имеет вид cxkjtq.q) = I; akjl^kjlto + siy (z) = «^-^(z) + Eik/z).
Среди них — радиальная базисная функция входного вектора – ошибка моделирования элемента , в предположении, что он также ограничен.
Используя нейросетевое моделирование, динамическое уравнение манипулятора странстве можно записать в виде
Mx(q)x + Cx(q,q)x + G^q) = Fx.
Среди них
™xkj(q) = 9kj^kjto + Edkj(q): cxkj Cq. q) = a^kj (z) + Eckj (z);
9xkW = Pk^M + ^gkW- в
про-
Используя матрицы GL и их операции умно- жения, можно записать с помощью ^(q)=[{9}T-p(q)}] + fM(q).
где и – матрицы GL, элементами которых являются и – ма трица, элементами которой являются ошибки моделирования .
Аналогично, для и существуют
Vw) = [raT №)j]+yz):
где , {B} — матрицы GL и векторы GL, элементами которых являются ; and
-
— элементы, матрицы ошибок моделирования и соответственно.
Предполагая, что 1 — это идеальная траектория рабочего пространства, тогда 2 и 2 — это идеальная скорость и идеальное ускорение.
(25) r(t) = xr(t) — x(t) = e(t) + Ae(t)
где Λ — положительно определенная матрица.
Лемма 1 (лемма Барбала): если функция h:R→R — равномерная непрерывная функция, определенная на [0,+∞), lim_(t→∞) ∫_0^th(δ)d существует и конечна, то lim_(t→∞)h(t)=0.
Лемма 2. Let , где * представляет собой свертку, и H (s)
является строго экспоненциально устойчивой передаточной функцией порядка n*n. Если , то непрерывно при t→∞
Рассмотрим систему SISO второго порядка, пусть , тогда мы можем получить и . Чтобы гарантировать, что H(s) является строго экспоненциально стабильной передаточной функцией, можно определить, что c>0. Если вышеуказанные условия выполнены и , можно получить , ce(t)+e(t)=0, что обеспечивает экспоненциальную замкнутость системы.
Используя i для представления оценочно- го значения, зададим , затем и представляют собой формулы {θ},
{A} и {B } оценки.
Конструктивно контроллер выполнен в виде
F. = [{9}T ■ (S(q)}K + [U}T ■ №)}K + где . Первые три члена регулятора – управление на основе модели, член K_r эквивалентен управлению с пропорциональной производной (PD), а последний член закона управления является надежным членом, который подавляет ошибку моделирования нейронной сети.
Из выражения регулятора очевидно, что регулятору не нужно решать обратную матрицу Якоби. В реальном управлении проигравший может быть получен с помощью .
Подставляя уравнения (23) и (24) в уравнения (21), можно получить
{[WT ■ P(q)}] + ^м(чЖ + <[{Л}Т ■ (Z(z)}] + ec(z№ Ч^ЧНШ + е^^р,.
Подставляя закон управления (26) в приведенную выше формулу, можно получить
{[{9}T ■ {S(q)}l + Ем№+ {[(Д}т - (Z(z)}] +
+5c(z)}x + [{B}T ■ (Я(д)}] + Ec(q) =
[{0}T " {5(q)}]xr + № ■ {7(z)}]zr +
+[{B}T ■ {W(q)}] + Kr + ks sgn(r).
Подставляя x=xr-r и x=xr-r в приведенное выше уравнение, мы можем получить
{[{6/ • {6(q)}l + EM(q)K^r - r) + {[{4}T. {Z(z)}] +
+EC (z)Xxr - r) + [{B}T ■ {//(q)}] + Eg (q) =
= [{9}T • [6(q)}]fr + [ЙГ' {Z(z)}]xr+ [] + Kr + kssgn(r)
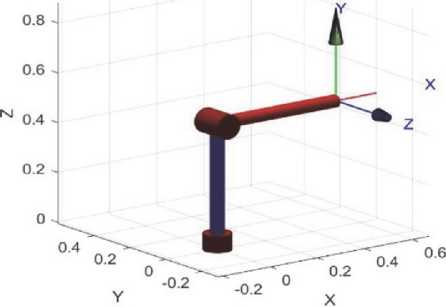
Подставляя уравнения (23) и (24) в приве- денные выше уравнения, мы можем получить МДд)т + Cx = [{9}T ■ (5(q)}]^r+!wT ■ {Z(z)}]ir + [{B}T ■ №)}] + E. Для замкнутой системы, если K>0,k,>//E//па- раллелен, а адаптивный закон устроен как вк = rk ■ {^k(q)}xtrk; (31) Pk = М^к^)тк. Среди них и и – векторы θ ˆ_k и a ˆ_k соответственно, тогда , непрерывно, и e^0 и e '^0 при t^“. В соответствии с интегральной линейной функцией Ляпунова, предложенной в ссылке, ее можно проанализировать на устойчивость следующим образом. V = 1 rTMk(q)r + ^2=1 ^k Гк-^к + Среди них Гк = Гкт>0;Qk = Q^> 0; Nk = Nk > 0 и и — векторы θ ˆ_k и a ˆ_k соответственно, тогда , непрерывно, и e^0 и e '^0 при t^“. В соответствии с интегральной линейной функцией Ляпунова, предложенной в ссылке, ее можно проанализировать на устойчивость следующим образом. V = ; rTMk(,q)r +1^=1 SkT vs, + Среди них Г_к „ Q_k „ N_ka являются положительно определенными парно-секундными матрицами. Производная по V, получаем У =гтМкг + |гтМкг+Е^1 57^^ + Так как матрица кососимметрична, то , можно получить приведенную выше формулу и = гт(м,г+с,г)-^., ^W -SL. "iQi^k-y., Wtfk- Подставляя уравнение (30) в приведенное выше уравнение, мы можем получить 7 = -r^Kr- i,rTsgn(r) + ^=1 (Мт ■ {{k(q)}xerte + Х?=1 ^ ■ Йьй)^^ +К=1Р^Мтк+тЧ-у,^ eiv;^-^ 40^-2^! Рткм^к. Подставим адаптивный закон (31) в формулу (36) и объединим неравенство парал лельно, получим Анализ конвергенции: (1) Из , из леммы , e∈L2 непрерывно, то при , (2) Из 7 < -ттК получаем 0 Следовательно, когда V(t)∈L., существуют , и В этом разделе представлены результаты моделирования, показывающие работу предлагаемого адаптивного нейроконтроллера. В этом разделе предложенная схема управления применяется к двухзвенному проекту, математическая модель которого была разработана в пакете Solidworks и импортирована в пакет MATLAB вторым поколением Simulink [22]. Изначально первое звено перемещается, а второе нет. Показано, что после обучения первого звена отрабатываются внешние возмущения. Затем второе звено начинает двигаться, а первое останавливается. После этого оба звена перемещаются, оказывая динамические возмущения на каждое звено. Его динамическое уравнение КГ„1 = р + Ql + Z/COS^Z) ql + qZcos^Z)]. ; -q2 q2sin(q2) -q2(ql+ q2)sin(q2) q2 qlsin(q2) 0 л _ [flcosql + 5 cos(ql + q2)l , где известное параметров v=12, q1=9, q2=8, g=9.8, внешние помехи системы ,d1=2, d2=3, d3=6 .Пред положим, что ожидаемые инструкции по отслеживанию угла звеньев и угловой скорости являются следующим уравнением qld = 1 + 0.2sin(0.5Trt); q2d = 1 — 0.2cos(0.5Trt). Начальное состояние системы [q1 q2 q3 q4]^T= [0.6 0.3 0.5 0.5]^T , предполагаем , . При моделировании используем формулу закона управления и формулу адаптивного закона: В нейронной сети RNF параметры функции Гаусса установлены на c=[-2 -1 0 1 2] и b=3 , начальный вес 0,1Т Параметры моделирования робота-манипулятора следующие: L(1):’qlim’, [-180 180]*deg;’m’, 0, ...’Jm’, 200e-6, ...’G’, -62.6111, ...’B’, 1.48e-3; L(2) :’qlim’,[-180 180]*deg ;’m’, 17.4, ...’Jm’, 200e-6, ...’G’, 107.815, ...’B’, .817e-3. Рис. 3. Механическая модель робота-манипулятора
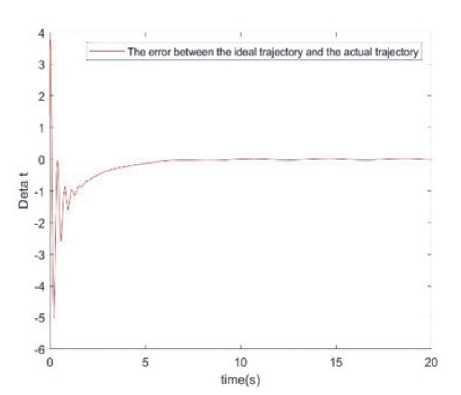
1) имитационное моделирование нейронных сетей ELman Из рис. 4 видно, что в случае адаптивной компенсации на начальном этапе имеет место некоторая степень возмущения, а угловая скорость и положение имеют тенденцию к сближению. Рис. 4. Аппроксимация угловой скорости и положения звена 1 и звена 2 в случае адаптивной компенсации Эльмана Рис. 5. Аппроксимация внешнего возмущения и функции f(x) с адаптивной компенсацией Эльмана Рис. 6. Ошибка между идеальной траекторией и реальной траекторией Из графиков (рис. 5, 6) видно, что возмущения практически полностью скомпенсированы, а процесс управления роботом вполне удовлетворительный. Экспериментальные результаты также доказывают, что предложенный подход достаточно устойчив к динамическим возмущениям, вызванным взаимным влиянием динамики звеньев. Предлагаемый метод управления является оригинальным и успешно использует преимущества SMC, нейросетевого и адаптивного управления.
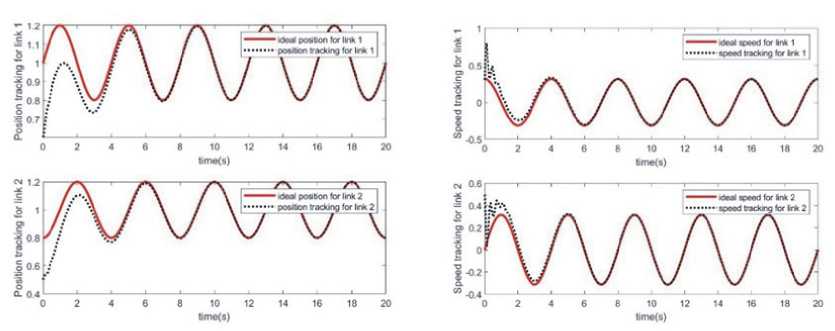
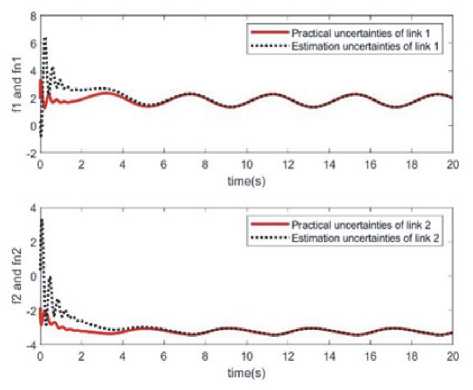
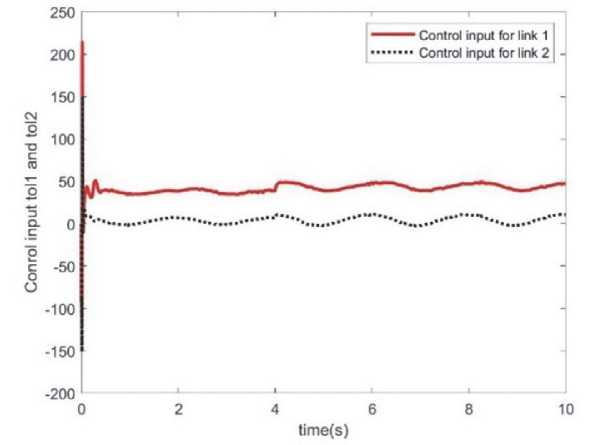
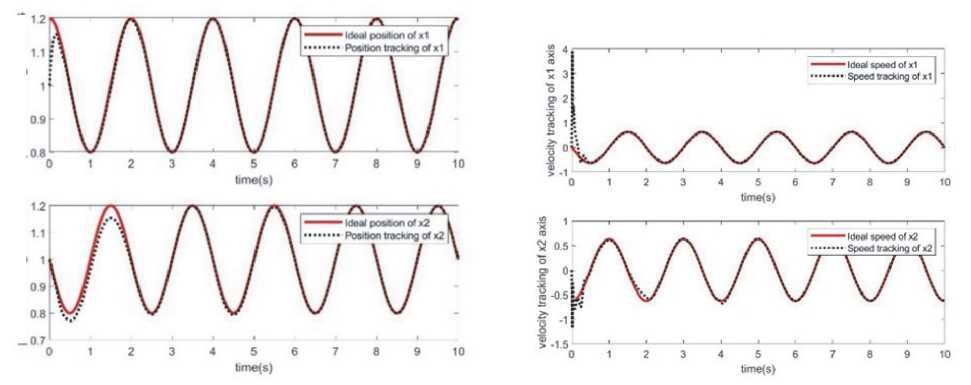
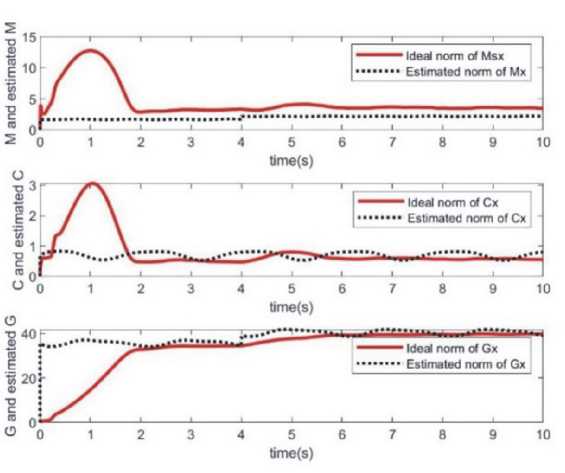
2) Имитационное моделирование нейронных сетей RBF Для аппроксимации каждого элемента Мх№ and GAq") входом нейронной сети RBF является q, рассчитанное количество точек скрытого слоя равно 7. Для аппроксимации каждого элемента Gx(q-q), вход нейронной сети RBF равен (q, q), а количество точек скрытого слоя дизайна равно 7. ПараметрывсехфункцийГауссапринимаются как Ci = [-1.5 -1.0 -0.5 0 0.5 1.0 1.5] и ^i = 10 , а начальное значение нейронной сети установлено равным 0 . Закон управления принимает формулу (26), а адаптивный закон принимает формулу (31). Выгода выби- „ [30 рается как К = [ ^],k_s=0,5. Из леммы 2 желательно, чтобы л [ o 15] . Параметры адаптивного закона (31) принимаются как \\ rk = diag[2.0},gk = diag{0.10] и jVk — diag{5.0) .. Результаты моделирования показаны на рис. 7 и рис. 8. Как видно из рис.8, в начале моделирования значение ошибки относительно велико из-за фазы обучения нейронной сети управляющему входу. Когда нейросетевой компенсатор проходит обучение, ошибки в основном аннулируются, а траектория движения и расчетное значение сходятся. Рис. 7. Вход управления для каналов 1 и каналов 2 Рис. 8. Аппроксимация угловой скорости и положения звена 1 и звена 2 в случае адаптивной компенсации RBF position tracking of x2 axis position tracking of x1 axis Рис. 9. Аппроксимация для переменных H^*(4)H- 11^(9,4)11 и 116,(4)11 Поскольку траектория слежения не является непрерывным возбуждением, оценочные значения 11^(4)11- lte)ll и I|G,O?)II не сходятся к ll^(l)lk IICrMII и HG,(q)l, которые часто встречаются в инженерной практике. Из моделирования двух нейронных сетей видно, что, хотя нейронная сеть RBF имеет более высокую скорость обучения и обучения при том же планировании траектории, общая точность ошибок меньше, чем у Элмана. Но если есть больше условий помех и неопределенной среды, общие результаты обучения RBF лучше. ЗАКЛЮЧЕНИЕ Таким образом, подводя итоги исследования, можно сделать следующие выводы. В ходе исследования качество выполнения роботом конкретных задач зависит не только от качества материала, из которого он изготовлен, качества подвижных частей, но и от качества математических моделей, в которых эффективность и точность управления роботом основаны на анализе его динамической модели и уменьшают погрешность между запланированной и фактической траекториями. В данной статье показана нейронная сеть, отличающаяся тем, что разработана модель двух адаптивной нейронной схемы управления нелинейными динамическими системами манипулятивного робота на основе рекуррентной сети Элмана. Обоснован выбор архитектуры сети и предложен алгоритм ее обучения методом сопряженных градиентов. Моделирование адаптивной нейронной сети RBF показывает, что хотя она имеет более быстрое время отклика, но при отсутствии непрерывного возбуждения система не сходится и значение ошибки намного больше, чем у сети Элмана. Модель вращения плоского манипулятора описывается дифференциальным уравнением первого порядка с переменной структурой и выходным уравнением. Модель имеет простую структуру и может быть использована, когда неизвестны внутренняя динамика и параметры управляемой системы. Компьютерное моделирование применения модели оптимального управления слежением за углом поворота манипулятора подтверждает теоретические положения и демонстрирует высокую эффективность ее функционирования. Этот метод также может быть применен к моделированию манипулятора с несколькими степенями свободы. В то же время модель может быть использована в методе адаптивного управления манипулятором после доработки.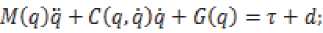
Список литературы Повышение точность работы робота за счет применения нейронных сети (нейронных компенсаторов и нелинейной динамики)
- A.-V. Duka, “Neural Network based Inverse Kinematics Solution for Trajectory Tracking of a Robotic Arm,” Procedia Technology, vol. 12, pp. 20–27, Dec. 2014, doi: 10.1016/j.protcy.2013.12.451.
- Y. H. Kim and F. L. Lewis, “Neural network output feedback control of robot manipulators,” IEEE Transactions on Robotics and Automation, vol. 15, no. 2, pp. 301–309, Apr. 1999, doi: 10.1109/70.760351.
- S. Islam and P. Liu, “Robust Sliding Mode Control for Robot Manipulators,” Industrial Electronics, IEEE Transactions on, vol. 58, pp. 2444–2453, Jul. 2011, doi: 10.1109/TIE.2010.2062472.
- Yazdanpanah M. J. and Karimian Khosrowshahi G., “Robust control of mobile robots using the computed torque plus H∞ compensation method,” 632249139440000000. https://www.sciencegate.app/document/10.1109/cdc.2003.1273069 (accessed Jun. 29, 2022).
- R. E. N, R. N. V, and Y. Zhengjie, “Neural network compensation of dynamic errors in a position control system of a robot manipulator,” Computing, Telecommunication and Control, vol. 64, no. 1, pp. 53–64, 2020, doi: 10.18721/JCSTCS.13105.
- F. W. Lewis, S. Jagannathan, and A. Yesildirak, Neural Network Control Of Robot Manipulators And Non- Linear Systems. CRC Press, 2020.
- K. Kara, T. Missoum, K. Hemsas, and M. Hadjili, “Control of a robotic manipulator using neural network based predictive control,” Dec. 2010, pp. 1104–1107. doi: 10.1109/ICECS.2010.5724709.
- S. Seshagiri and H. Khalil, “Output Feedback Control of Nonlinear Systems Using RBF Neural Networks,” Neural Networks, IEEE Transactions on, vol. 11, pp. 69–79, Feb. 2000, doi: 10.1109/72.822511.
- I. V. Tetko, V. Kůrková, P. Karpov, and F. Theis, Artifi cial Neural Networks and Machine Learning – ICANN 2019: Theoretical Neural Computation: 28th International Conference on Artifi cial Neural Networks, Munich, Germany, September 17–19, 2019, Proceedings, Part I. Springer Nature, 2019.
- M. W. Spong and M. Vidyasagar, Robot dynamics and control. New York: John Wiley & Sons, 1989.
- Y. Zhengjie, E. Rostova, and N. Rostov, “Neural Network Compensation of Dynamic Errors in a Robot Manipulator Programmed Control System,” 2020, pp. 554–563. doi: 10.1007/978-3-030-34983-7_54.
- L. Y.-J, T. S.-C, W. D, L. T.-S, and C. C.l.p, “Adaptive neural output feedback controller design with reduced-order observer for a class of uncertain nonlinear SISO Systems,” UM, vol. 22, no. 8, 2011, doi: 10.1109/TNN.2011.2159865.
- Z. Liu, G. Lai, Y. Zhang, X. Chen, and C. Chen, “Adaptive Neural Control for a Class of Nonlinear Time-Varying Delay Systems With Unknown Hysteresis,” IEEE transactions on neural networks and learning systems, vol. 25, pp. 2129–40, Dec. 2014, doi: 10.1109/TNNLS.2014.2305717.
- N. Duan and H.-F. Min, “NN-based output tracking for more general stochastic nonlinear systems with unknown control coeffi cients,” Int. J. Autom. Comput., vol. 14, no. 3, pp. 350–359, Jun. 2017, doi: 10.1007/s11633-015-0936-4.
- B. Luo, D. Liu, X. Yang, and H. Ma, “H ∞ Control Synthesis for Linear Parabolic PDE Systems with Model-Free Policy Iteration,” in Advances in Neural Networks – ISNN 2015, Cham, 2015, pp. 81–90. doi: 10.1007/978-3-319-25393-0_10.
- C. Chen, Z. Liu, K. Xie, Y. Zhang, and C. L. Philip Chen, “Adaptive neural control of MIMO stochastic systems with unknown high-frequency gains,” Inf. Sci., vol. 418, no. C, pp. 513–530, Dec. 2017, doi: 10.1016/j.ins.2017.08.027.
- Y. Chen, J. Liu, H. Wang, Z. Pan, and S. Han, “Modelfree based adaptive RBF neural network control for a rehabilitation exoskeleton,” Jun. 2019, pp. 4208–4213. doi: 10.1109/CCDC.2019.8833204.
- M. Wang and A. Yang, “Dynamic Learning From Adaptive Neural Control of Robot Manipulators With Prescribed Performance,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 47, no. 8, pp. 2244–2255, 2017, doi: 10.1109/TSMC.2016.2645942.
- M.-D. Tran and H.-J. Kang, “Nonsingular Terminal Sliding Mode Control of Uncertain Second-Order Nonlinear Systems,” Mathematical Problems in Engineering, vol. 2015, p. e181737, Oct. 2015, doi: 10.1155/2015/181737.
- R. Ortega and M. W. Spong, “Adaptive motion control of rigid robots: a tutorial,” in Proceedings of the 27th IEEE Conference on Decision and Control, 1988, pp. 1575–1584 vol.2. doi: 10.1109/CDC.1988.194594.
- S. S. Ge, C. C. Hang, and L. C. Woon, “Adaptive neural network control of robot manipulators in task space,” IEEE Transactions on Industrial Electronics, vol. 44, no. 6, pp. 746–752, 1997, doi: 10.1109/41.649934.
- “Design and implementation of a RoBO-2L MATLAB toolbox for a motion control of a robotic manipulator.” https://ieeexplore.ieee.org/document/7473678/ (accessed Jun. 30, 2022).
- S. Kh. Zabihifar, A. Kh. D. Markazi, and A. S. Yushchenko, “Two link manipulator control using fuzzy sliding mode approach,” Herald of the Bauman Moscow State Technical University. Series Instrument Engineering, Dec. 2015, doi: 10.18698/0236-3933-2015-6-30-45.


