Повышение точности измерений уровня жидкости в замкнутых движущихся резервуарах

ВВЕДЕНИЕ. ОБЗОР СУЩЕСТВУЮЩИХ МЕТОДОВ

Проблема точного определения уровня жидкости в резервуарах достаточно актуальна на сегодняшний день. Особую значимость она принимает при транспортировке дефицитных материалов и использовании жидкого топлива, т. к. даже небольшая погрешность в измерениях приводит к потере имеющихся ресурсов. Так, предприятия транспортной отрасли используют все известные способы экономии топлива, однако требуются новые, более прогрессивные системы измерения и их разработки для дальнейшего развития отрасли и ее направлений.

Рассмотрим технические средства, существующие на текущий момент для определения уровня жидкости в резервуарах. На основе различных физических методов существует достаточно широкая группа устройств контроля и измерений. В настоящее время распространение получили поплавковые, буйковые, гидростатические, электрические, ультразвуковые, радиоизотопные, а также визуальные средства контроля.

При их разработке учитываются такие физические и химические свойства контролируемой среды, как температура, давление, нагревание, охлаждение, электрическая проводимость и другие. Особое внимание необходимо уделять характеру движения жидкости и резервуара. По характеру движения измерение можно разделить:

Табл. 1. Средства измерения уровня жидкости в резервуаре

Вид средств измерения	Техническая реализация
Визуальные	1)    уровнемерные линейки, 2)    уровнемерные рейки, 3)    уровнемерные стекла
Поплавковые	1)    поплавковые выключатели, 2)    буйковые датчики
Гидростатические	1)    манометры (различных видов), 2)    гидростатические зонды
Электрические	По виду чувствительного элемента разделяют: 1)    емкостные (емкостные уровнемеры), 2)    кондуктометрические (концевые выключатели)
Электр омагнитные	Датчики направленного электромагнитного излучения
Акустические	Датчики, работающие по принципу локации: ультразвуковые, определяющие время прохождения сигнала

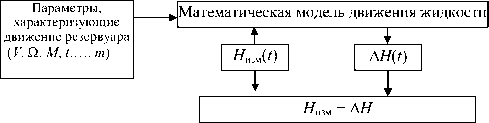
Рис. 1. Схема включения в процедуру измерений математической модели.

H изм ( t ) — измеренный уровень жидкости с помощью штатных приборов; Δ H ( t ) — поправка уровня жидкости; H изм + Δ H — реальные значения уровня жидкости c определенной ошибкой; ( V , Ω , M , t ,…, m ) — значения линейных и угловых скоростей движения объекта, массы резервуара и времени движения и др. параметры движения резервуара c жидкостью

• 1)    на статическое (жидкость и резервуар в покое);

• 2)    динамическое (резервуар находится в движении);

• 3)    смешанное (включает первые два).

Наибольшей интерес для исследования представляют 2) и 3) случаи (жидкость "плещется" в резервуаре), т. к. в их рассмотрении возникают трудности и при моделировании движения, и при выборе средств и методики определения уровня жидкости. Существующие средства измерения представлены в табл. 1. Степень распространения этих средств можно оценить в процентном соотношении так: 24 % — поплавковые датчики, 20 — гидростатические, 15 — емкостные, 5 — кондуктометрические, 21 — электромагнитные средства, 15 % — акустические средства.

Как видно из табл. 1, существует большое количество приборов и методов измерения жидкости.

РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ, ВКЛЮЧАЕМОЙ В КОНТУР ИЗМЕРЕНИЙ

В развитие и усовершенствование существующих средств предлагается система измерения уровня жидкости c включением математической модели в контур измерения. Основной принцип построения этой системы для одномерного случая представлен на рис. 1.

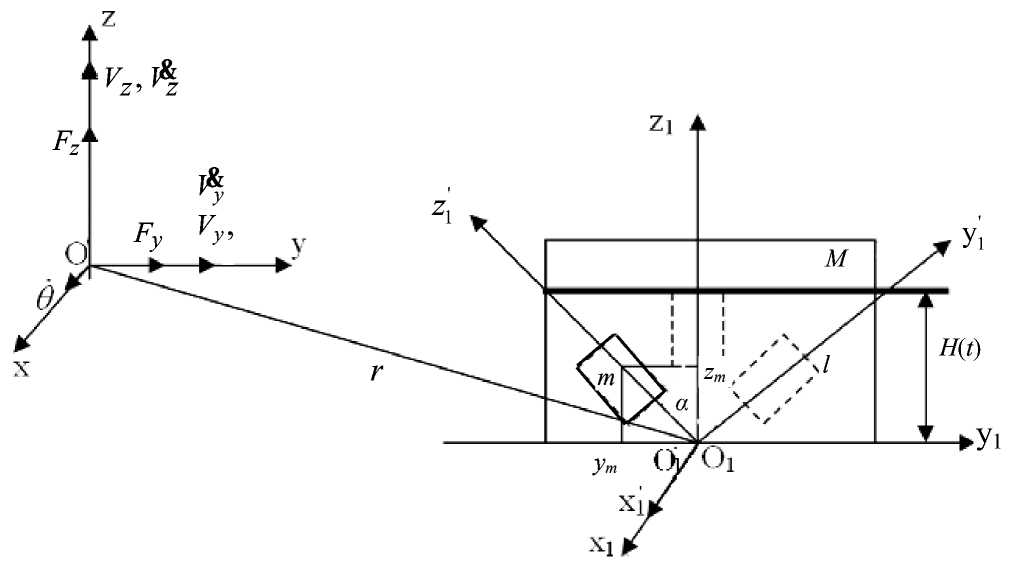
Рис. 2. Рассчитываемая модель жидкости в емкости — твердотельный маятник.

Oxyz — система координат, связанная с основанием (подвижным объектом); Ox 1 y 1 z 1 — система координат жидкостной емкости массой M ; Ox₁ ^' y₁ ^' z₁ ^' — система координат зеркального отражения качающегося на подвесе длиной l маятника массой m ; H ( t ) — высота над поверхностью концевой точки качающегося маятника

В режиме реального времени производится измерение уровня жидкости с помощью штатных приборов и корректировка на основе "Математической модели движения жидкости". На вход модели поступают значения линейных и угловых скоростей движения объекта ( V , Q ), массы резервуара и жидкости в нем ( M , m ), характеристики подвижного объекта и т. д.. Далее организуется итерационный процесс вычисления поправки \ К к H изм в зависимости от параметров движения основания.

Рассмотрим построение математической модели, используемой в такой системе измерения уровня жидкости. Построим простейшую модель для случая плоского (в вертикальной плоскости) движения объекта (основания) с жидкостным резервуаром при следующих допущениях. Точка приложения к объекту сил, определяющих движение, находится вне резервуара: на рис. 2 — (·) О, система координат Oxyz, действующие силы F y , F z (проекции на оси y, z), компоненты скорости и ускорения — V y , V z , V ^& _y , V ^& _z (движение в плоскости yz), θ — угол тангажа. Жидкость в резервуаре представляется твердым телом с переменной массой m ( t ); растекание жидкости по внутренним стенкам резервуара не учитывается; движение жидкости отображается зеркально относительно горизонтальной плоскости физическим маятником (рис. 2); масса маятника сосредоточена в центре масс, а точка подвеса прикреплена к середине днища резервуара на расстоянии r от (·) О основания; в этом случае угол отклонения нормали к поверхности жидкости при движении будет соответствовать углу α отклонения этого маятника от исходного положения (рис. 2.)

Введем систему координат O 1 x 1 y 1 z 1 , начало которой совпадает с точкой крепления маятника к основанию. Система координат O ^' x₁ ^' y₁ ^' z₁ ^' связана с зеркальным отображением твердотельного висящего маятником (см. рис. 2); α — угол отклонения маятника; l — длина маятника; m и M — масса жидкости и резервуара соответственно.

Для построения уравнений движения жидкости в резервуаре воспользуемся формализмом Лагранжа.

Составим выражения, необходимые для формирования уравнения Лагранжа:

У т = l sin а , z m = l cos a , (1) где y m , z m — проекции центра тяжести маятника на соответствующие оси;

M r = m t ² r ² , 2)

• где M r — центробежный момент инерции , r — отстояние системы координат, связанной с резервуаром, от системы Oxyz;

Fz = mV,  Fy = mV,(3)

где F z , F y — проекции сил, действующие на маятник со стороны основания, на оси Oz и Oy;

Qa = ymFz — ZmFy • где Qα — обобщенная сила, действующая на маятник.

Составим выражения для кинетической и потенциальной энергий замкнутой системы:

T = 2 m (Vz2 + Vy2) + 2 ml2 (a + p )2,(5)

П = - mgl cos

1 2 a + ^ C ( l cos a )

где С — жесткость стенок резервуара, p — проекция угловой скорости.

Составим выражения для функции Лагранжа:

d a = ml ² (* p ' •

^- = mgl sin a - Cl ² sin a , d α

Тогда в соответствии с уравнением Лагранжа и в предположении, что масса и длина маятника не меняются на каком-то промежутке времени t i <  t <  t i +1 :

dfdL^—dL _ dt ( d aJ d a

_ ml ² ( &+ p ) - mgl sin a + Cl ² sin a _

Откуда получим:

ml ²<&- mgl sin a + Cl ² sin a _

_-ml2p+ mlVz sin a - mlVy cos a + mt^2r2.(9)

Разделив левые и правые части уравнения (9) на ml ², получим:

gC aet—sin a +_ lm

1            V ^& y          θ ^&2 r ²

_-jp + -(V sin a —-cos a + —— lz ll2

Откуда:

a s+

V m

l

l J                    l 11

Табл. 2. Зависимость массы топлива в топливном резервуаре самолета от времени полета

Времязависимая величина	Время t , мин
	14	15.2	30.7	65.17	92.17
Масса топлива m , т	24.2	24.1	21.2	1.7	0.14

m , т

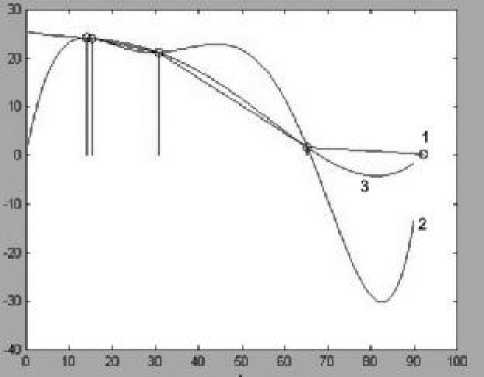
t , мин

Рис. 3. Графическая зависимость массы топлива в резервуаре от времени полета самолета, и ее полиноминальная аппроксимация:

1 — ломаной;

2 — m ( t ) = –0.0001 t ⁴ + 0.0103 t ³ – 0.3410 t ² + 4.828 t ;

3 — m ( t ) = –0.0004 t ³ + 0.0103 t ² – 0.1658 t + 25.4845

+ C ₂ sin

C

m

^g l

t + a о ,

Если предположить, что ввиду малости угла α sin a ~ a , то выражение (11) можно представить в виде

& + f \ ( t ) a = Ф ( t ) ,                 (12)

где ϕ ( t ) =

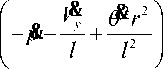
f 1 ( t ) =

f C

^^^^^^^

g

^^^^^^^

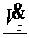
l

V m

l

Если f 1 ( t ) > 0, то левая часть выражения (12) представляется характеристическим уравнением, и общее решение такого уравнения — линейная комбинация sin ω t и cos ω t :

a ( t ) = C 1 cos

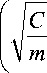
^g l

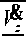
l

t +

где постоянные коэффициенты C 1 и C 2 могут быть найдены из начальных условий; α 0 — ошибка.

В общем случае решение уравнения (12) сводится к известному уравнению Хилла—Матье [3]. Аналитическое решение таких уравнений затруднительно. Однако по уравнению (12) можно сделать оценку угла отклонения α как функции скоростей и ускорений движения основания. Численное решение такого уравнения выполняется на бортовой вычислительной машине, в результате чего определяется поправка A H ( t ) (рис. 1).

В общем случае необходимо учитывать изменение массы и длины маятника от времени. Опытные данные изменения массы топлива в топливном баке, например, самолета [2], зафиксированные в определенные промежутки времени, приведены в табл. 2. Используя измеренные значения массы топлива в топливном резервуаре, можно построить функцию изменения массы топлива от времени m ( t ). Полиномиальная аппроксимация этой функции приведена на рис. 3.

Таким образом, (если принять аналитическую аппроксимацию 3 (рис. 3)) изменение массы топлива как функция времени в этом частном случае имеет вид

m ( t ) =

= –0.0004 t ³ + 0.0103 t ² – 0.1658 t + 25.4845. (14)

В любом случае уровень жидкости, измеренный датчиком, можно отождествить с высотой расположения конца физического маятника H ( t ) (рис. 2), причем справедливы выражения:

H ( t ) = l ( t ) cos α , l ( t ) = Ф( m ( t )), (15) где α — угол отклонения маятника, l ( t ) — длина маятника, которая является функцией времени и зависит от изменения массы жидкости. Функцию l ( t ) = Ф( m ( t )) можно предварительно определить по конструкции резервуара.

ЗАКЛЮЧЕНИЕ

Построение математической модели по предложенному способу для пространственной задачи осуществляется также на основе уравнений Лагранжа II рода и реализуется на бортовой вычислительной машине с помощью программно*го пакета "Построение математических моделей"*). Построение модели средствами этой программы базируется на описании кинематической схемы, в которой указаны параметры взаимного расположения рассматриваемого подвижного объекта, резервуара и жидкости в нем.

В заключение следует отметить, что предложенный способ повышения точности измерения уровня жидкости в замкнутом резервуаре может быть реализован на любых подвижных объектах, имеющих замкнутые резервуары с жидкостью, нуждающиеся в измерении уровня. Реализация возможна с помощью бортовых программно-аппаратных средств, разработка которых осуществляется вышеназванной САПР.