Повышение точности контроля проплавления при электронно-лучевой сварке

В настоящее время вопросы стабилизации заданной глубины проплавления при электронно-лучевой сварке (ЭЛС) остаются актуальными, особенно на заключительных этапах сборки ответственных узлов. Мы уже рассматривали способ контроля и стабилизации глубины проплавления по рентгеновскому излучению, регистрируемому со стороны ввода электронного луча [1]. Способ основан на определении положения максимума интенсивности рентгеновского излучения, соответствующего текущей глубине проплавления при заданных режимах ЭЛС (рис. 1). Определение максимума интенсивности осуществляется коллимированным рентгеновским датчиком на основе кристалла NaJ(Tl).

На датчик попадает часть рентгеновского излучения J д ( z ) в пределах, ограниченных шириной коллиматора Δ, величина которой по оси z составляет Δ/sinφ и определяется выражением

д

2sin ф               2

J д ( S _z ) = J max J e -°^{,4 (} z ^-E z ) dz ,         (1)

д

2sin ф

• - °,4 ( z -S- )²

где e z – плотность распределения рентгеновского излучения по оси z ; ε z – смещение пятна нагрева относительно заданной глубины проплавления.

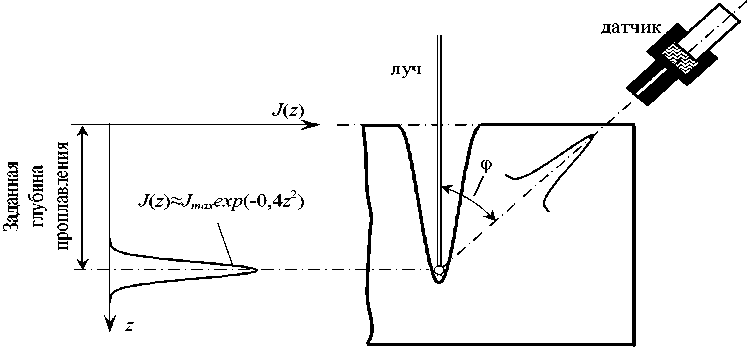
Рис. 1. Распределение интенсивности рентгеновского излучения по глубине канала проплавления ( а ) и схема регистрации излучения ( б )

Представим ε z в виде

ε z = ε z 0 + ε zm sinα,

где ε z 0 – постоянная составляющая смещения пятна нагрева относительно заданной глубины проплавления; ε zm – амплитуда переменной составляющей смещения пятна нагрева относительно заданной глубины проплавления; α = ω t ; ω = частота переменной составляющей; t – время.

Представление (2) отражает тот факт, что в поло-

жение пятна нагрева введено поисковое движение с частотой ω и амплитудой ε zm . Это может быть реализовано, например, введением переменной составляющей в ток электронного сварочного луча или колебаниями коллиматора относительно проекции пятна

нагрева.

При подстановке выражения (2) в (1) последнее может быть представлено рядом Фурье в тригонометрической форме:

да

Jд (е_л) = a⁰ + Z (

² k = 1

a_k cos a + b_k sin a ) ,

где а k , b k – коэффициенты ряда:

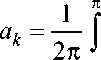
-П

2sin ф                         2

^{- 0,4} ( z ^-E z 0 ^-E zm ^{sin a} ) J_

J max J e                  ^zz

A ^^^^^B ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^_ 2sin ф

cos k a d a;

вии смещения и меняют знак при изменении направления смещения пятна нагрева относительно заданного положения (рис. 2). Изменение знака свидетельствует об изменении фазы колебаний данной составляющей на 180 ^о .

Характер зависимостей этих составляющих предполагает очевидный простой способ получения информации о глубине проплавления, заключающийся, например, в синхронном детектировании сигнала датчика рентгеновского излучения, т. е. выделении составляющей с частотой ω и использовании ее для управления параметрами ЭЛС (током луча или током фокусирующей системы), от которых зависит глубина проплавления.

Если положение пятна нагрева совпадает с осью рентгеновского датчика, то амплитуды косинусоидальных составляющих а 2 , а 4 , ... (четные гармоники) максимальны (рис. 3).

Составляющая с двойной частотой поискового движения а 2 может использоваться, например, для определения амплитуды поискового движения, при которой обеспечивается наибольшая чувствительность способа. Так, из формулы (3) можно определить зависимость а 2 от ε zm при ε z 0 = 0:

n bk= ri

2n

-n

A

2sin ф                         2

^{- 0,4} ( ^{z -E} z 0 ^-E zm sin ^a ) max J e

A

2sin ф

sin k a d a . (4)

1 ⁿ a ^{2 ( S} zm ) = 2^^J

-n

0,3

2sin ф

0,3

^^» ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

2sin ф

cos2a d a.

Анализ приведенных соотношений свидетельствует о том, что при наличии в положении пятна нагрева поискового движения по глубине канала проплавления спектральный состав ренгеновского излучения (РИ) дополняется составляющими с частотами, кратными частоте поискового движения и амплитудами, находящимися в определенной зависимости от положения пятна нагрева относительно заданной глубины проплавления.

Так амплитуды синусоидальных составляющих b k с частотами (2 n + 1)ω, где n = 0, 1, ..., пропорциональны в некоторых пределах смещению пятна нагрева относительно заданной глубины проплавления (положения коллиматора). Они равны нулю при отсутст-

График зависимости (5) показывает, что максимальная чувствительность может быть достигнута при амплитуде поискового движения, составляющей 2–3 % от глубины проплавления (рис. 4).

Влияние амплитуды поискового движения на зависимость амплитуды b 1 от положения ε z0 пятна нагрева относительно заданной глубины проплавления представлено на рис. 5. Зависимости рассчитаны в соответствии с выражением:

1 n bl (E z 0 )= J 2n

n

0,3

2sin ф                         2

^{- 0,4} ( ^{z -E} z 0 ^-E zm ^{sin a} ) max J e

- 0,3 2sin ф

sin a d a

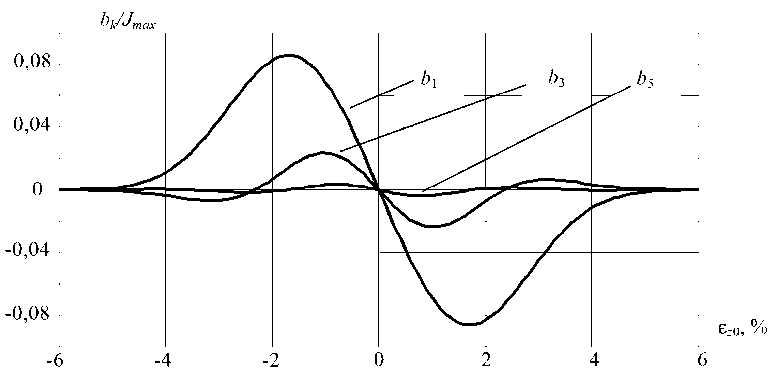
Рис. 2. Зависимости амплитуд синусоидальных b k составляющих от смещения пятна нагрева относительно заданной глубины проплавления: Δ = 0,1 мм; φ = 45 0

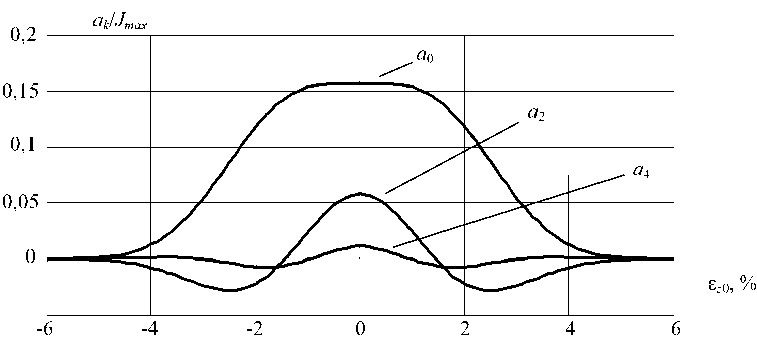
Рис. 3. Зависимости амплитуд косинусоидальных составляющих a k от смещения пятна нагрева относительно заданной глубины проплавления: Δ = 0,1 мм; φ = 45 0

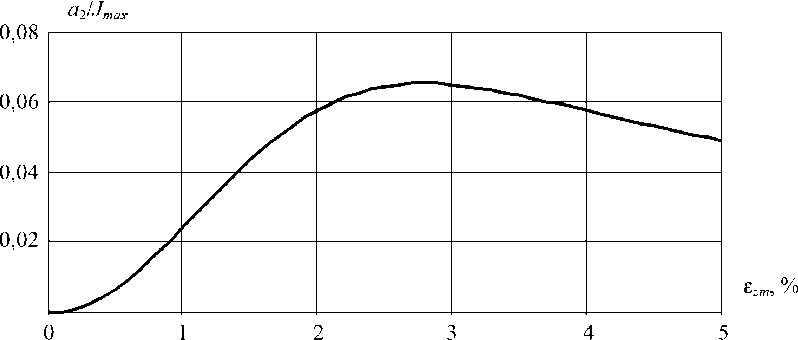
Рис. 4. Зависимость амплитуды а 2 от амплитуды поискового движения ε zm .

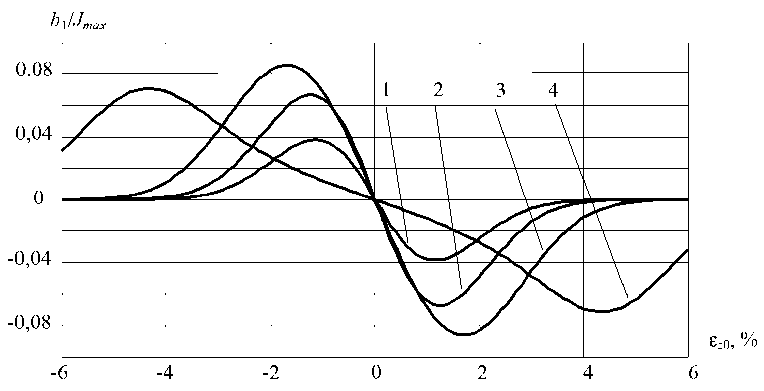
Рис. 5. Зависимости амплитуды b 1 от смещения пятна нагрева относительно заданной глубины проплавления (30 мм) при различной амплитуде ε zm (в процентах от глубины проплавления):

1 – ε zm = 0,5; 2 – ε zm = 1; 3 – ε zm = 2; 4 – ε zm = 5

Из графиков видно, что с увеличением амплитуды поискового движения до определенного значения (εzm = 2) увеличивается коэффициент преобразования и область линейности характеристики (кривые 1–3). Дальнейшее увеличение амплитуды ведет к уменьшению коэффициента преобразования b1/εz0 (кривая 4), что подтверждается экстремальной зависимостью амплитуды а2 от амплитуды εzm поискового движения (рис. 4).

Представляет интерес зависимость рассмотренных характеристик от ширины коллиматора. На рис. 6 представлено семейство характеристик b 1 (ε z 0 ) при различных Δ и ε zm , рассчитанных по формуле:

b l ( e z 0 , ^A , ⁸ zm ) =

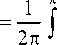
-Л

Д

2sin ф                          2

^{- 0,}4 ( z —8 z о —8 zm sin a)² ,

J max J e                   ^uz

Д

2sin ф sin ada.

В широком диапазоне амплитуд поискового движения (0,1–3 % от глубины проплавления) коэффициент преобразования максимален при ширине коллиматора, составляющей 2–3,5 % от глубины проплавления (рис. 6, кривые 4 , 5 ). Так, при глубине проплавления 30 мм приведенные проценты соответствуют амплитуде поискового движения – 0,03–0,9 мм и ширине коллиматора – 0,6–1 мм.

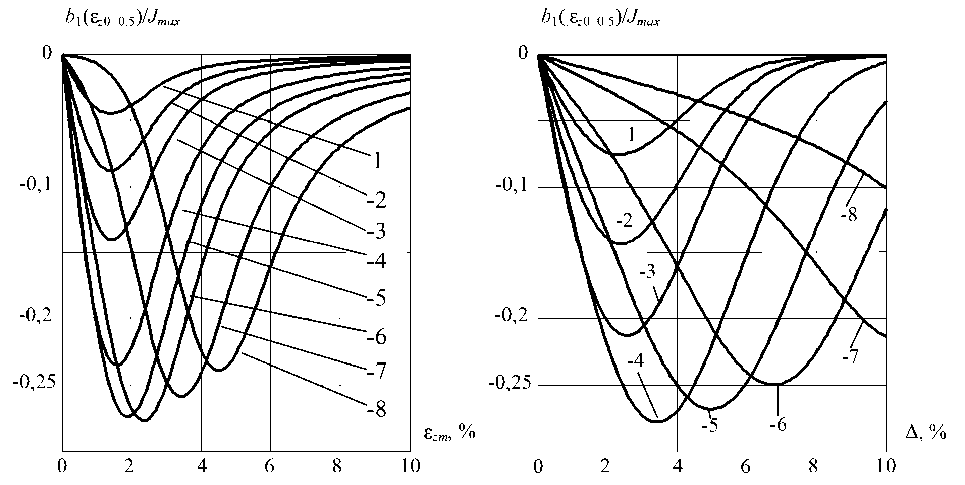
Это подтверждается и характеристиками, полученными решением (6) при подстановке ε z 0 = 0,5 (введено постоянное смещение пятна нагрева от заданной глубины проплавления) и варьировании амплитудой поискового движения ε zm , и шириной коллиматора Δ (рис. 7). Максимальное значение составляющей рентгеновского излучения b 1 при смещении пятна нагрева на 0,5 % от глубины проплавления достигается в одном случае при ε zm ≈ 2,5 % и Δ ≈ 3 % от глубины проплавления (рис. 7, а , кривая 6 ), в другом – при ε zm ≈ 2 % и Δ ≈ 3 %.

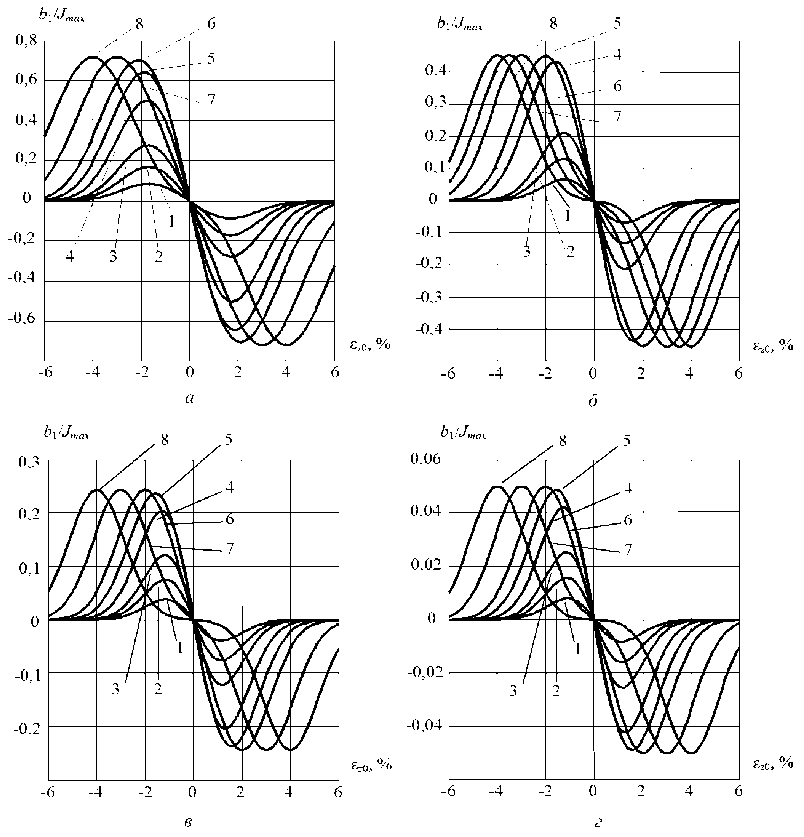
Рис. 6. Графики зависимости амплитуды b 1 от смещения пятна нагрева относительно заданной глубины проплавления при различных амплитудах ε zm поискового движения и различной ширине Δ коллиматора рентгеновского датчика: а – ε zm = 2; б – ε zm = 1; в – ε zm = 0,5; г – ε zm = 0,1; 1 – Δ = 0,3; 2 – Δ = 0,6; 3 – Δ = 1; 4 – Δ = 2; 5 – Δ = 3; 6 – Δ = 4;

7 – Δ = 6; 8 – Δ = 8 (ε zm и Δ – в процентах от глубины проплавления)

б

Рис. 7. Зависимость b 1 (0,5) от амплитуды ε zm поискового движения при различной ширине коллиматора Δ ( а ) и от ширины коллиматора Δ при различной амплитуде ε zm поискового движения ( б ):

1 – Δ = ε zm = 0,3; 2 – Δ= ε zm = 0,6; 3 – Δ= ε zm = 1; 4 – Δ = ε zm = 2; 5 – Δ = ε zm = 3; 6 – Δ= ε zm = 4; 7 – Δ= ε zm = 6; 8 – Δ= ε zm = 8

Результаты аналитических исследований использованы при технической реализации устройств стабилизации глубины проплавления, внедряемых в технологические комплексы ЭЛС ряда предприятий, что подтверждает возможность практического применения математической модели рентгеновского датчика глубины проплавления.

Таким образом, введение поискового движения приводит к появлению в спектре рентгеновского излучения гармонических составляющих, несущих информацию о глубине проплавления; составляющая с двойной частотой может использоваться для определения амплитуды поискового движения при которой обеспечивается наибольшая чувствительность способа; полученные соотношения позволяют производить анализ информационных сигналов для определения условий получения наибольшей чувствительности датчика при оптимальной ширине коллиматора.