Повышение точности позиционирования внутритрубных снарядов с использованием данных ГЛОНАСС/GPS

Реализуемые в настоящее время крупные проекты по строительству магистральных трубопроводов (МТ), старение старых, повышение объемов добычи и транспортировки углеводородного сырья на фоне ужесточающихся требований по безопасности и экологичности заставляют по-новому взглянуть на аспекты мониторинга и диагностики состояния магистральных трубопроводов. Получившая в последнее время широкое распространение технология внутритрубной неразрушающей дефектоскопии с использованием автономных внутритрубных инспекционных снарядов (ВИС) позволила многократно повысить надежность и безаварийность магистральных трубопроводов [1]. При этом наряду с высокими достижениями в области внутритрубной дефектоскопии имеются очевидные проблемы навигационного обеспечения данных измерений и контроля пространственного положения подземных и подводных трубопроводов. В частности, должны быть решены следующие задачи:

– определены с высокой точностью географических координат дефекты ВИС, при этом вскрытие трубопровода должно быть минимальным;

– определены с высокой точностью географических координат траектории ВИС для контроля пространственного положения МТ.

Контроль пространственного положения МТ с целью своевременного обнаружения оползней, провалов, пучинистостей и других трубопроводными операторами России в настоящее время не проводится из-за отсутствия эффективных методик и аппаратуры. В середине 90-х гг. развитие технологий инерциальной навигации позволило создавать ВИС на борту с бесплатформенной инерциальной навигационной системы (БИНС). Однако основная задача системы – ориентации снаряда – высокая точность – не решается из-за низкой точности автономных БИНС. Значения основных инструментальных среднеквадратиче- ских погрешностей некоторых серийно выпускаемых инерциальных навигационных систем (ИНС) (полуаналитической ИНС «Маршрут», выполненной на поплавковых гироскопах, бесплат-форменных «Lasernav», созданных на лазерных гироскопах, и «LITEF», в основу которых легли динамически настраиваемые гироскопы), приведены в табл. 1.

В таблице приводятся только значения m г в связи с идентичностью характера влияния погрешностей β и погрешностей коэффициентов mr , а также их примерного равенства β ≈ m _г . Результаты расчета погрешностей координат, вызванных различными инструментальными погрешностями ИНС (табл. 1), с использованием аналитических выражений, полученных в [2], приведены в табл. 2. Расчет проведен на основе исходных данных:

– погрешности координат вызванные β и m г рассчитаны для максимальной амплитуды угловых движений ВИС А = 2 град;

– интервал корреляции τ кор смещения нуля акселерометра, характеризующий его изменчивость, принят равным 2 ч;

– временные интервалы движения Т приняты 300 и 500 с, что при средней скорости движения ВИС V ≈ 4 м/с соответствует длине траектории пройденных участков L 0 1,2 и 2 км, что соответствует типовому расстоянию между маркерными пунктами при внутритрубной диагностике;

– принимается непрямолинейность траектории т. е. L ⊥ = L = L 0 /2, где L ⊥ – длина траектории в поперечном направлении, L – длина траектории в продольном направлении.

Значение ошибки начальной выставки по курсу α _z и отвечающая ей погрешность начальной выставки по курсу соответствуют режиму двойного гирокомпасирования или использования промежуточной реперной точки (числитель) и режиму гирокомпасирования (знаменатель) (табл. 1, 2).

Таблица 1

Название ИНС	Значение основных инструментальных погрешностей (СКО)
	Δω , град/ч	V ω , град/ч	V δ , угл. с	Δ a, угл. с	V a , угл. с	m а, рад	m г, рад	α z, угл. с / угл. мин
«Маршрут»	5 ⋅ 10 - 3	–	1	0,5	2	10 –5	10 –4	30 / 2,5
«Lasernav»	8 ⋅ 10 - 3	2 ⋅ 10 - 3	–	3	2	5 ⋅ 10 - 5	5 ⋅ 10 - 6	30 / 3,5
«LITEF»	3 ⋅ 10 - 2	1 ⋅ 10 - 2	–	10	1	10 - 4	10 - 4	30 / 13

Таблица 2

Инструментальная погрешность БИНС	Выражение для оценки влияния	Погрешность координат на времени Т (« Маршрут » / « Lasernav » / « LITEF »), см
		T = 300 с	T = 500 с
Постоянная скорость ухода ( Δω )	~ 3 Δω gT 6	110 / 173 / 675	495 / 792 / 2969
Белошумная скорость ухода гироскопа ( V ω )	~ 5/2 V gT ω    20	– / 3 / 16	– / 11 / 59
Белошумная ошибка гироскопической следящей системы ( V δ )	g ~ T 3/2 V δ     3	13 / – / –	50 / – / –
Погрешность установки β и масштаба m г гироскопа	3 m Г g 6 платформенная	40 / – / –	204 / – / –
	T 2 m Г Аg ~ 2	– / 8 / 160	– / 21 / 428
Нестабильность смещения нуля акселерометра ( Δ а )	~ 5/2 Δ а g 1/2 кор	16 / 94 / 312	56 / 340 / 1134
Белошумная ошибка акселерометра ( V a )	~ 3/2 V gT a 3	16	80
Погрешность масштаба акселерометра ( m а )	maL	1 / 3/ 6	1 / 5/ 10
Погрешность начальной выставки по курсу	α zL ⊥	____[15]____ [45/63/234]	____[50]____ [75/105/390]

Исходя из результатов расчетов (табл. 2), можно сделать вывод, что автономные ИНС без коррекции не позволяют достичь требуемой точности определения координат трубопровода. Известно, что при проектировании и эксплуатации магистральных трубопроводов большое значение имеет точность координатной информации, например в приложениях, касающихся измерений пространственного положения МТ и изменений пространственного положения, а также при проведении обследования состояний подводных участков МТ требуемая точность определения координат составляет ±0,5 м [3]. Для достижения такой точности и решения поставленных задач могут быть использованы спутниковые радионавигационные системы в комплексе с оборудованием ИНС внутритрубного инспектирующего снаряда (рис. 1).

Система представляет собой комплекс для определения координат продольной оси МТ с использованием ВИС, оснащенного интегрированной БИНС, корректируемой с использованием наружных аппаратных средств (маркеров). Система функционирует в двух режимах: режиме сбора данных и режиме последующей обработки. Она может быть охарактеризована как система с обзорно-сравнительным методом коррекции, использующим априорные сведения о координатах отдельных точек трубопровода, определенных в данном случае по сигналам СРНС ГЛОНАСС/GPS [4]. Специфика внутритрубной диагностики МТ на основе применения ВИС заключается в том, что измерительная информация на борту ВИС не обрабатывается, записываются только показания датчиков для последующей обработки на ЭВМ. Таким образом, разделяются во времени операция сбора и обработки диагностической информации. Предлагается также разделить по времени операцию сбора показаний датчиков ИНС и операцию их постобработки в наземной подсистеме, функциональная схема которой приведена на рис. 2. Для комплексирования данных БИНС, показаний системы одометров снаряда и данных спутниковой радионавигационной системы (СРНС) используется расширенный фильтр Калмана и сглаживающий алгоритм. Задачей фильтра Калмана является оценка вектора погрешностей БИНС и одометра.

Вектор состояния S , оцениваемый фильтром Калмана (рис. 3) описывается выражением

S = (Ψ,δV,δk,δα,δβ,Δω,ΔA)Т, где Ψ – вектор погрешности пространственного положения снаряда, определенного по данным ИНС; δV – вектор погрешности скорости; ΔА – нестабильность смещения нуля акселерометров; Δω – постоянная скорость ухода гироскопов; δk – погрешность корректирующего коэффициент масштаба одометра; δα, δβ – погрешность корректирующих коэффициентов учитывающих погрешность установки гироскопических элементов по осям снаряда.

Навигационные спутники

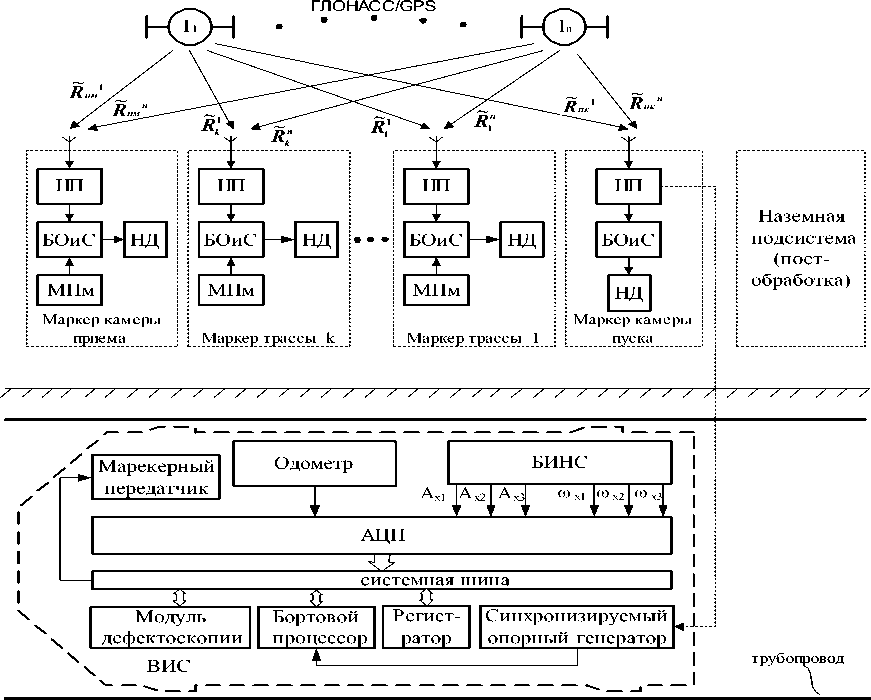
Рис. 1. Структурная схема системы комплексного обследования магистральных трубопроводов: НП – навигационный приемник; БОиС – блок обработки и сопряжения; МПм – маркерный приемник; НД – накопитель данных

~

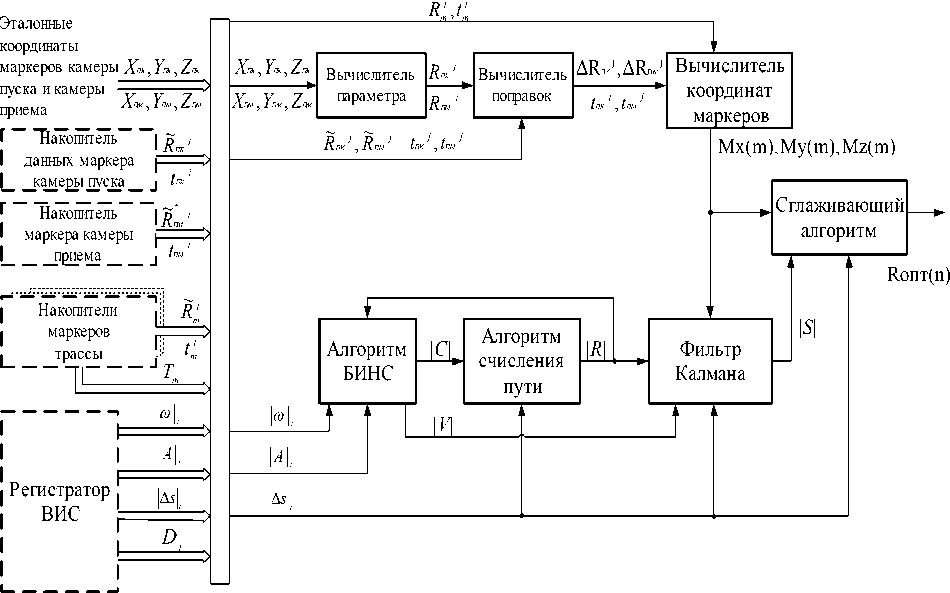
Рис. 2. Функциональная схема наземной подсистемы

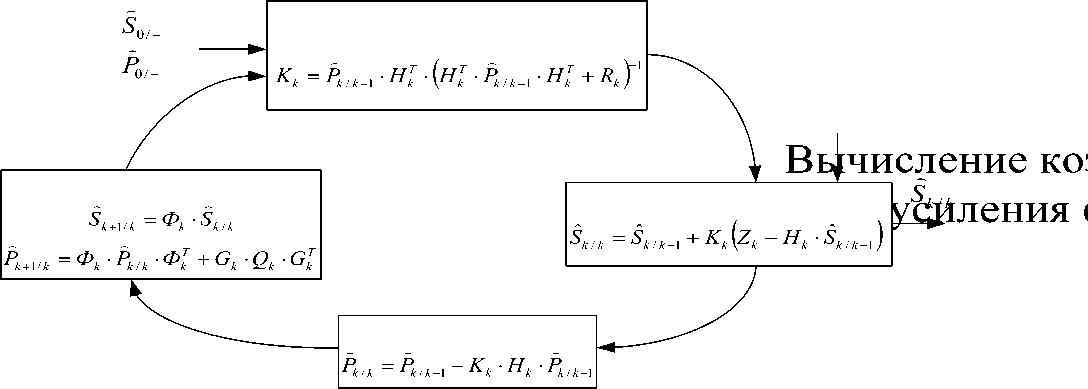
Рис. 3. Структура оптимального фильтра

Вектор измерений Z представляет собой вектор погрешностей и формируется как разность одноименных показаний ИНС и одометра, ИНС и СРНС. Вектор измерений на основе данных одо-

метра определяется по выражению

z 1

^z = ^{z 2}

z 3

tj

j V • 1 X 1 dt - k A s ( j )

t j - 1

tj

j V • 1 х 2 dt - aA s ( j ) t j - 1

tj

j V • 1 х 3 dt - PA s ( j ) . tj - 1

,

где V – вектор скорости, полученный по результатам измерений БИНС, k – корректирующий коэффициент масштаба одометра; a , в - корректирующие коэффициенты, учитывающие погрешность установки гироскопических элементов; t j –1 – временное соответствие началу j -го интервала замеров; t j – временное соответствие концу j -го интервала замеров, A s ( j' ) - показания одометра - расстояние, пройденное за j -й интервал замеров; 1 х 1 , 1 х 2 , 1 х 3 – единичные векторы, определяющие 3 ортогональных оси снаряда, положение которых в географической системе координат характеризуется строками матрицы направляющих косинусов С . При формировании вектора измерений с использованием данных СРНС применяется разность координат двух соседних маркеров (относительные координаты). Вектор измерений, полу-

ченный на основе данных о координатах маркеров, определенных по сигналам СРСН, в первом случае представляет собой погрешность счисления и формируется как разность счисленного положения маркера и положения маркера, определенного СРНС, или в относительных координатах:

z 4

orHC'^

z 6

Rx( m) - Rx( m - 1) Ry ( m ) - Ry ( m - 1) Rz ( m) - Rz ( m - 1)

Mx( m) - Mx( m - 1) My( m) - My( m - 1) Mz( m) - Mz( m - 1)

где Rx ( m ), Ry ( m ), Rz ( m ) – счисленные координаты ВИС, соответствующие маркеру m ; Mx ( m ), My ( m ), M z( m ) – координаты маркера m , определенные по данным СРСН.

Во втором случае координаты, соответствующие положению маркеров m и m – 1, полученные по данным БИНС (интегрированием инерциального вектора скорости V ), сравниваются с коор-

динатами маркеров, полученных по данным СРНС или, в относительных координатах,

z 7

z = z 8

z 9

tN j Vxdt tN-1

tN j Vydt tN-1

tN j Vzdt

. tN - 1

Mx ( m ) - Mx ( m - 1) My ( m ) - My ( m - 1)

Mz ( m ) - Mz ( m - 1)

Полученный вектор погрешностей S используется в сглаживающем алгоритме, где происходит коррекция показаний БИНС, пересчет матрицы направляющих косинусов С , и на основании откорректированных данных заново запускается алгоритм счисления пути. Счисление для каждого участка между маркерами m и m – 1 начинается с точно известного положения маркера m – 1. Очевидно, что погрешность счисления нарастает по мере удаления от маркера m – 1 и достигает максимального значения в точке m . Запуск в блоке

оптимального сглаживания алгоритма счисления пути в обратном направлении с точно известного положения маркера m , формирует траекторию, погрешность которой минимальна у маркера m и максимальна в точке m – 1. Оптимальная, комбинированная из прямого и обратного счисления пути оценка координат снаряда в каждой из

n точек меду маркерами k и k + 1 определится по выражению

R опт ⁽ n ) = ^{( Р} прям ⁽ n ) - 1 + ^Робр ⁽ n ) - 1 ) ^X

X ( R прям ( n ) Р прям ( n ) - 1 + R обр ( n ) Р обр ( n ) ^- 1 ), где R прям ( n ), R обр ( n ) – векторы счисленных координат во внутренней точке n меду маркерами k и k + 1 для прямого и обратного счисления соответственно; P прям ( n ), P обр ( n ) – ковариационные матрицы погрешности для прямого и обратного счисления соответственно.

Учитывая, что T , 5a , 50 , 5 k меняются на интервале между маркерами медленно, принимается, что они постоянны. Ковариационные матрицы погрешности для прямого и обратного направления описываются выражениями

^Рпрям ⁽ n) = M ( ⁵ R прям ⁽ n ^{) 5} R Tпрям ⁽ n ) ) = H прям ⁽ n) ^X X M( zz^T ) H T прям ( n ) = H прям ( n ) p ( m ) H T прям ( n );

Р обр ( n ) = m ( 5 R обр ( n ) 5 R^T обр ( n ) ) = H обр ( n ) X X M( zz T ) H T обр ( n ) = H обр ( n ) p ( m ) H T обр ( n ), где M – оператор математического ожидания; Н прям ( n ), H обр ( n ) – матрицы измерения; z – вектор погрешности    z = [ T x T y T z 5 k 5a 50 ] ;

p ( N ) – ковариационная матрица погрешности вектора z .

Таким образом, на выходе блока оптимального сглаживания для каждого интервала между маркерами получаем исправленные координаты ВИС R опт ( n ) в каждой n точке интервала.

Кроме описанного выше алгоритма коррекции данных БИНС точность определения координат в системе повышается за счет привязки временной шкалы измерительной системы к временной шкале спутниковой радионавигационной системы L1…Ln, тем самым повышается точность взаимной синхронизации меток времени системы маркеров и оборудования внутритрубного инспектирующего снаряда. Для этих целей перед пуском ВИС в камере пуска синхронизируемый опорный генератор соединяется с навигационным приемником камеры пуска на время, требуемое для синхронизации. Использование аппаратуры МРК-23 в составе комплекса маркеров позволит обеспечить синхронизацию временной шкалы снаряда и маркеров с погрешностью до 150 нс и определить координаты маркеров со среднеквадратической погрешностью ±5 см в относительном режиме. В качестве опорных станций используют маркер камеры приема и маркер камеры пуска при условии, что эталонные координаты фазовых центров антенн навигационных приемников известны.

Для оценки погрешностей системы проводилось математической моделирование разработанных алгоритмов комплексирования с использованием пакета MathCAD 2001 Professional с соблюдением следующих условий:

– применялась система БИНС «Lasernav» с использованием лазерных гироскопов;

– расстояние между маркерами составляло 2 км;

– погрешность системы одометров равнялась ±0,5 %;

– погрешность определения координат маркеров составляла ±0,5 см.

По результатам моделирования погрешность определения координат трубопровода в области максимальной погрешности (в центре участка между маркерами) составила ± 0,5 м. При уменьшении расстояния между маркерами до 500 м погрешность определяется погрешностью координат маркеров.

Разработанные алгоритмы и система могут быть использованы для определения пространственного положение подземного трубопровода с погрешностью менее 1 м. Это позволит применять результаты периодических траекторных измерений для контроля изменений пространственного положения трубопровода и оценки напряженных состояний, определения координат дефектов, а в комплексе с гидрографическими промерными системами – контролировать состояние подводных участков МТ.