Повышение точности прогнозирования макроэкономических процессов посредством учета взаимосвязей между ними

При построении комплексных прогностических систем макроэкономических процессов исследователи зачастую прибегают к использованию регрессионного инструментария. Данный подход является одним из наиболее распространенных и позволяет получать не только точечные оценки значений прогнозируемых показателей, но и находить доверительные интервалы для данных значений с заданным уровнем надежности. В большинстве случаев каждый из рассматриваемых показателей моделируется и предсказывается согласно построенной специально для него модели отдельно от других. Таким образом, прогнозируемые индикаторы зачастую получаются либо несогласованными друг с другом, либо один из функционально связанных показателей прогнозируется через предсказания, полученные по остальным индикаторам. Например, при предсказании индексов Валового Внутреннего Продукта (ВВП), дефлятора ВВП и ВВП, выраженного в постоянных ценах, используется известная функциональная связь, а именно что индекс ВВП равен произведению индекса дефлятора ВВП на индекс реального ВВП. В связи с этим обычно строятся модели только для двух из данных показателей, а прогноз для третьего получается посредством выражения его значения через предсказания этих моделей. Однако при таком подходе теряется информация, которая могла бы быть получена из результатов работы модели для третьего показателя, что можно охарактеризовать как существенное упущение, так как данная информация могла бы улучшить полученные прогнозы. В работе высказывается идея того, что существует возможность повысить точность прогнозов функционально и корреляционно зависимых показателей, если после прогнозирования каждого из них по отдельности провести процедуру поправок полученных предсказаний посредством учета взаимосвязей между ними. Так как система статистического учета процессов, происходящих в экономике на макроуровне, предполагает множество функциональных и корреляционных взаимосвязей между измеряемыми характеристиками экономической структуры, предлагаемый метод поправок предсказаний регрессионных моделей имеет достаточно широкую сферу применения. Следует отметить, что идеи, в некоторой мере напоминающие те, которые высказываются в данной научной работе, уже были опубликованы в некоторых международных статистических журналах и рассматривают регрессию с множественным откликом, т.е. моделирующую вектор целевых переменных. Такие модели состоят из системы регрессионных уравнений с предположением о некоторой степени корреляционной взаимосвязи между предсказываемыми целевыми переменными. Некоторое количество работ было посвящено непараметрическим моделям с двумя целевыми переменными, оцениваемых с помощью сглаживающих сплайнов, см. например Wang et al. (2000), Chen and Wang (2011), Welsh and Yee (2006) и Lestari et al. (2010), а также с применением полиномиального приближения, см. работу Chamidah et al. (2012). Целью таких моделей с множественным откликом является получение более точных предсказаний, чем по моделям с одной целевой переменной, так как в последнем случае учитывается только влияние объясняющих факторов на выходную переменную, а в первом добавляется информация о взаимозависимости между прогнозируемыми откликами. Данная взаимозависимость обычно представляется в виде дисперсионноковариационной матрицы ошибок, которая используется для взвешивания наблюдаемых отклонений при расчете оценок истинных параметров моделей по аналогии с обобщенным методом наименьших квадратов. Максимальный эффект в таком случае достигается при наличии достаточно сильной корреляционной взаимосвязи между анализируемыми откликами, что явно показано в работах Ruchstuhl et al. (2000), Welsh et al. (2002) и Guo (2002). Обычно регрессионные модели с множественными откликами широко применяются при анализе категориальных или панельных данных в области медицины и социологии, см. работы Wang et al. (2000), Chen and Wang (2011), Welsh and Yee (2006) и Antoniadis and Sapatinas (2007). Однако и в области экономики подходы, разделяющие схожую идею, могут давать повышенное качество моделей. Предпосылкой для данного улучшения точности прогнозов, как уже было сказано выше, является факт наличия функциональных и сильных корреляционных зависимостей среди основных макроэкономических индикаторов, которые могут быть использованы для повышения надежности разрабатываемых моделей.

МЕТОД УЧЕТА ФУНКЦИОНАЛЬНЫХ И КОРРЕЛЯЦИОННЫХ ЗАВИСИМОСТЕЙ МЕЖДУ МАКРОЭКОНОМИЧЕСКИМИ

ИНДИКАТОРАМИ

Пусть Уу,, X_t: t = 1,^,n } является рассматриваемым набором действительных данных, где y _t - целевая переменная, а X_t = (1,% 1 _t ,x ₂₁ , — ,* m _t ) — конечный набор объясняющих переменных. Тогда линейная регрессионная модель для y _t выглядит следующим образом:

y_t = XtB + e или У t = x_tB ,

где В - вектор-столбец параметров модели, рассчитываемый стандартным способом:

B = (XTX) 1XTY.

Также предположим выполнение следующих предпосылок.

Предпосылка 1: Строгая экзогенность ошибок, т.е. Е^е^Х) = 0;

Предпосылка 2: Гомоскедастичность ошибок, т.е. Е(^ |.Y) = а ²;

Предпосылка 3: Нормальность ошибок, т.е. E _t ~V(0; tr);

Предпосылка 4: Отсутствие полной мультиколлинеарности, т.е. Х^ТХ является положительно определенной матрицей;

Предпосылка 5:   Отсутствие автокорреляции остатков, т.е.

COV^E^Ej^) = 0, VІ ^ j.

Тогда функция плотности вероятности для прогнозного значения на один шаг вперед у _п+г является сдвинутым и масштабированным t -распределением с v = п — m — 1 степенями свободы.

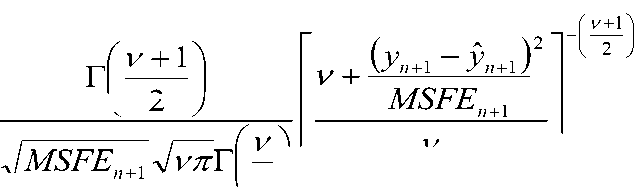
V + 1

’ п + 1 - y n + 1

MSFE„ + i

V

Т ( У п + 1 ) =

где у-n ₊1 является параметром сдвига и рассчитывается по формуле (2), а - параметром масштаба и вычисляется стандартным способом согласно следующей формуле:

MSFE, = х ² ( 1 + X T , ( X T X ) ^{- 1} X_t+ ,) t + г           у          t + i \          /       t + г J

где    - вектор-столбец значений объясняющих переменных, участвующих в построении прогноза на период t + i, s2 - несмещенная оценка дисперсии ошибок, рассчитывающаяся следующим образом:

s

n

КУ - у)2

г = 1

n - m -1

Далее предположим, что имеется набор целевых переменных у ⁽¹⁾, у⁽²\ .„, у^(К^, каждая из которых моделируется с помощью набора данных X ⁽^,Х(^,_,Х^(К^ соответственно, а также что все рассматриваемые целевые переменные связаны между собой некоторой функциональной зависимостью:

• У⁽ ' ) = f ( У ⁽⁰ .--. y ⁽ i ^{- 1 )} , - ; -¹ ' ,..- У,¹ K ) ) , (7) где / j обозначает функцию, которая выражает у⁽⁾ через остальные целевые переменные.

Для обеспечения надежности получаемых далее выводов предположим выполнение еще одной предпосылки:

Предпосылка 6: Отсутствие корреляции остатков рассматриваемых целевых переменных, т.е. cov^ ((^ ; s^^ = 0, Vi^ j. Особо отметим, что данное условие обычно выполняется при моделировании векторов с достаточно большим числом макроэкономических индикаторов и их волатильности сравнимы по величине.

Тогда существует возможность провести корректировки полученных прогнозов, учитывая полученные функции плотности вероятности и известную функциональную связь между целевыми переменными. Данную процедуру предлагается проводить с помощью Метода Максимального Правдоподобия (ММП, англ. Maximum Likelihood Estimation), который был проанализирован, рекомендован и значительно популяризован Р. Фишером между 1912 и 1922 гг. Суть метода сводится к максимизации так называемой функции правдоподобия, которая представляет собой совместную плотность вероятности набора анализируемых случайных величин. В случае с упомянутыми выше функционально зависимыми целевыми переменными совместная плотность вероятности может быть представлена следующим образом с использованием функции Д:

II | Ч> f f[y ⁽²⁾ _v ⁽³⁾ _v ^{( K} ^•Mr'fl/²) ^K ))

LH = ^ 1 ^{( f} 1 L yn + 1 , yn + 1 ,..., yn + 1 J/ ^ 2 ⁽ yn + 1 ^)/Y ^ K ⁽ yn + 1 ) . ⁽⁸⁾

Таким образом процедура корректировки полученных прогнозов сводится к поиску таких значений прогнозируемых случайных величин, которые максимизировали бы выражение (8). С целью снижения вычислительной сложности расчета оптимальных параметров при максимизации функции правдоподобия (8) прибегнем к процедуре логарифмирования совместной плотности вероятности, что даст в результате сумму рассматриваемых функций вместо их произведения.

T H f f Tv(-) i/3) K)№+fi/-) + K log - LH - т{^1(fi[yn+1, yn+1,..., yn+1 ])} + Ш{ү- (yn+1 Д + Л + lnt^K (yn+1 )} . (9)

Поскольку логарифм является монотонно возрастающей функцией, то значения аргументов, максимизирующих выражения (8) и (9), будут совпадать. С учетом степени развития вычислительных технологий на данный момент поиск такого решения осуществляется за приемлемое время даже при условии, что число рассматриваемых целевых переменных достаточно большое.

Помимо проводимых корректировок полученных прогнозов можно также получить скорректированную функцию плотности вероятности для всех целевых переменных под рассмотрением. Данную процедуру предлагается проводить с помощью вычисления маргинального распределения для анализируемой целевой переменной, которое учитывает вероятностные распределения остальных выходных переменных и функциональную связь между ними. Таким образом, согласно данному способу, скорректированная функция плотности вероятности вычисляется как показано ниже:

Pdf (yn1)- . П(yn'+1 )

Jn(yn1 )dy+

-^

где нормировочная константа в знаменателе представляет собой интеграл функции правдоподобия по всем целевым переменным под рассмотрением, а

^ (y^+ij вычисляется следующим образом:

^   ^

^ ( y n + 1 ) - J a J ^ 1 ( yW ) л Y , - , (f - 1 [ y®, y^,... y n 'f- ) , y n' + 1 ..., y tK ) ]) .

-^  -^

. Y ( y n + 1 ) л Y K ( y nK 1 ) ) dy n + 1 л dy n + ¹ ) dy n ^^ Л dy nK) .

Таким образом из исходного вероятностного распределения для целевой переменной получается скорректированная функция плотности вероятности, при этом дисперсия скорректированного распределения будет меньше либо равна дисперсии исходного, см. рисунок 1.

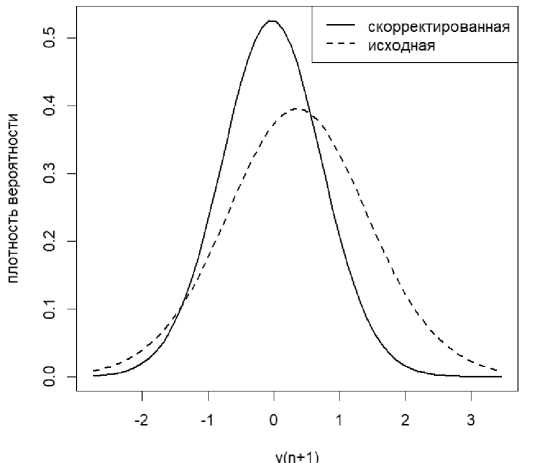
Рисунок 1. Пример скорректированной и исходной функций плотности вероятности

Как видно из рисунка 1, моды скорректированной и исходной функций распределения различны, что говорит о присутствии некоторой поправки прогнозируемого значения, поскольку мода скорректированного распределения соответствует точке максимума функции правдоподобия.

Далее рассмотрим ситуацию, когда набор рассматриваемых целевых переменных не связан строгой функциональной зависимостью, но при этом присутствует сильная корреляционная зависимость между моделируемыми случайными величинами. Предположим строится система моделей для целевых переменных у⁽¹\у⁽²\ ... ,у^(к\ каждая из которых моделируется с помощью набора данных Х⁽¹⁾, X⁽²⁾, ^,Х^(к ) соответственно, а также что все рассматриваемые целевые переменные связаны между собой некоторой линейной корреляционной зависимостью:

_v ( i ) ₌ *( i ) ₊ ^( i ) _V(D ₊ ^ i ) _v(2) _{+   +} *( i О к ) _{+ е}( i )

yt     0 ⁺ 1 yt ⁺ 2 y t ⁺ ••• ⁺ к yt  ⁺ et .          ⁽¹²⁾

Тогда, согласно модели (12), функция плотности вероятности для прогнозируемого значения целевой переменной у^^ является сдвинутым и масштабированным t -распределением с v = п — К — 1 степенями свободы.

• ⁽ i )    v^{( 1 )} v⁽ i ^{- 1 )} v⁽ i ^{+ 1 )} v⁽ K )І— Ч^п⁽ i ) MSFE⁽ i ) и —

Фіу У п + 1 y n + 1 ,..., y n + 1 , y n + 1 ,•••, y n + 1 /    ^ x y n + 1 , ^MSFE n + 1 , n K ^{1 )} , ⁽¹³⁾

где

v ⁽ i ) =b⁽ i ⁾+b⁽- i )v^{( 1 )} +b⁽ i )v^{( 2)} +    +Z>⁽ i M K )

y n + 1 ^b0 ^{+ b} 1 y n + 1 ^{+ b} 2 y n + 1 ⁺ ••• ^{+ b}K y n + 1 ,             ⁽¹⁴⁾

а MSFEn+1 - параметр масштаба, который вычисляется стандартным способом согласно формуле (5).

Отсюда делаем вывод, что если домножить совместную плотность вероятности на плотность данного распределения, то получится функция правдоподобия, которая учитывает корреляционную взаимосвязь между рассматриваемыми целевыми переменными. В формуле ниже приведена функция правдоподобия для вычисления поправки для i-ой целевой переменной.

• (i)         fv(D          MK)Y(v(i>lv(1)     v(i-1) v(i+1)     v(K))

^LH\ yn + 1 )   ^T 1 V yn + 1 y^v ^ KVn + 1 / Y iV" + 11 yn + 1,.-., yn + 1 , yn + 1 ,-.-, yn + 1 /• ⁽¹⁵⁾

Из формулы (15) легко заметить, что параметры функции <р j , а именно параметр масштаба и параметр сдвига зависят от неизвестных нам на момент (1)     (2)        (І-1)    (І+1)         (К)

прогнозирования величин уп+1, УП+1, ^ Уп+1 , Уп+1 , ^, Уп+1, по которым строится регрессия на величину у^^і • Поэтому при вычислении функции правдоподобия функции ^ ^У^^і) и Фі (Уп+і) имеют одно и то же значение аргумента, однако у первой параметры постоянны, а у второй – зависят от значений, принимаемых остальными целевыми переменными в процессе оптимизации. Здесь следует особо отметить, что несмотря на то, что в результате максимизации функции правдоподобия (15) поправкам подвергаются все рассматриваемые целевые переменные, данную функцию правдоподобия нецелесообразно использовать для вычисления поправки отличной от У^+і величины. Рекомендуется при вычислении поправок для каждой из рассматриваемых целевых переменных использовать отдельную функцию правдоподобия, в которой корректируемая целевая переменная выражается через остальные с помощью линии регрессии. Исходя из вида формулы (15) можно сказать, что поправки, полученные при регрессии одной из целевых переменных на все остальные не равны поправкам при регрессии другой целевой переменной на все оставшиеся. Рассчитываемые корректировки будут совпадать только в случае строгой функциональной связи между выходными переменными под рассмотрением. Таким образом возникает проблема выбора между получившимися корректировками, которую в данной научной работе предлагается решить посредством выбора той корректировки, при проведении которой корректируемая целевая переменная моделируется через остальные с помощью линии регрессии. Действуя таким образом, можно добиться более существенного улучшения качества получаемых прогнозов.

Для вычисления исправленной функции плотности будем по аналогии с предыдущим случаем вычислять маргинальное распределение для анализируемой целевой переменной, которое учитывает вероятностные распределения остальных выходных переменных и корреляционную связь между ними. Таким образом, согласно данному способу, скорректированная функция плотности вероятности вычисляется как показано ниже:

Pdf (yn21 )       “ІУ'"11

/ “ ( yn 21 W„ 21

-^

где нормировочная константа в знаменателе представляет собой интеграл функции правдоподобия по всем целевым переменным под рассмотрением, а

П ( y^J вычисляется следующим образом:

Ю   ю

~(y⁽ i )           Гч^т^1н      (v⁽² )K т(у⁽ i )         (у¹ K )У

“V y n + 1/ / ^л J ^Т 1 \ ^yn + 1/ ^Т 2 \ ^yn + 1 ^yV ^ iVn + 1 ^{yv T} K\^yn + 1/

-ю -^

• ^ -⁽ уП i + 1 уП +

V¹ i ^-1) y¹ i ⁺¹⁾ y¹ K )К⁽¹⁾ Л dv i ^-1)dv⁽ i ⁺¹⁾Л dv^K ) y n + 1 , y n + 1 v, y n + 1 dyn + 1 ^Л dy n + 1 dy n + 1 ^Л dy n + 1^.

ЭМПИРИЧЕСКОЕ И ИМИТАЦИОННОЕ ТЕСТИРОВАНИЕ МЕТОДА УЧЕТА ФУНКЦИОНАЛЬНЫХ И КОРРЕЛЯЦИОННЫХ

ЗАВИСИМОСТЕЙ

С целью тестирования эффективности предлагаемых в данной работе методов проведем имитационные и эмпирические эксперименты. Сначала проверим насколько хорошо работает разработанная система поправок для искусственно сгенерированных данных при наличии функциональной связи между прогнозируемыми переменными. Рассмотрим простейший случай, когда моделируются три целевые переменные y _1t , у ₂₁ и у _{з t} с помощью однофакторной линейной регрессионной модели, а именно:

У11 = ^10 + Ри xit + £11, y21 = в20 + в21 x21 + £21,                      (18)

y 3 1 = ^в 30 ^{+ в} 31 x 3 1 ^{+ £} 31 .

Причем моделируемые целевые переменные связаны функциональной зависимостью у з t = yl t + у 3. • Объясняющие переменные х 11 и х 21 генерируются исходя из нормального распределения с нулевой средней и единичной дисперсией, а переменная хзt - с помощью функциональной связи %з t = хг t + х21. Истинные параметры данного эксперимента устанавливались на уровнях рг0 = 2, р2о = 2, Р11 = 0.7 и 2211 = 0.7. Истинные ошибки первых двух моделей генерируются исходя из нормального распределения с нулевой средней и единичной дисперсией, а именно: £]_ t~/V(0,1) и £2t~./V(0,1). По третьей модели истинные коэффициенты и ошибки в явном виде не генерируются, поскольку и определяются функционально согласно значениям факторов и целевых переменных по первым двум моделям.

В таблице 1 представлена среднеквадратическая реализованная ошибка прогноза для моделей (18), обозначенных как , и , а также для моделей с учетом предложенных поправок ( , , ) и для моделей с учетом всех объясняющих переменных системы, приведенных ниже:

^~ y _{1 t}

c 10 + c ll x lt + c 12 x 2 1 + c 13 x 3 1 ,

~ y21 = c20 + c21 xl1 + c22x21 + c23x31,                  (19)

~ y31 = C30 + c31 xlt + C32x21 + c33x31.

Для обеспечения всеобъемлющего имитационного эксперимента описанные модели тестировались на окнах данных различной длины ( ) и сравнивались по показателю среднеквадратической реализованной ошибки прогноза, для расчета каждой из которых использовалось по 10 000 имитаций. Исходя из этого, полученные в результате эксперимента данные можно рассматривать в качестве основания для того, чтобы сделать состоятельные выводы относительно эффективности работы предлагаемых методов.

Таблица 1. Сравнение анализируемых методов, имитационный эксперимент, функциональная зависимость

^H , Ук _____ У2( Уз( Ук У2( Уз( Ук У2( Уз(

5	1.8019	1.8276	3.5756	1.6442	1.6751	3.1601	3.4469	4.0148	7.8445
6	1.5515	1.5467	3.0982	1.4703	1.4768	2.8733	2.3229	2.3652	4.7144
7	1.4329	1.4091	2.7944	1.3656	1.3667	2.6249	1.8767	1.8832	3.7273
8	1.3962	1.3734	2.7777	1.3517	1.3329	2.6383	1.7161	1.7349	3.4859
9	1.3225	1.2916	2.5672	1.2927	1.2604	2.4694	1.6013	1.5391	3.0879
10	1.2638	1.3012	2.5377	1.2414	1.2768	2.4443	1.4808	1.5111	2.9322
15	1.1418	1.1421	2.3064	1.1293	1.1299	2.2582	1.2341	1.2623	2.5204
20	1.0857	1.1089	2.1876	1.0776	1.0991	2.1631	1.1575	1.1763	2.3346
50	1.0217	1.0273	2.0583	1.0189	1.0263	2.0527	1.0432	1.0533	2.1087
80	1.0151	1.0275	2.0108	1.0149	1.0263	2.0069	1.0292	1.0371	2.0383
100	1.0209	1.0005	2.0009	1.0212	0.9995	1.9939	1.0339	1.0107	2.0215

Как видно из таблицы 1, предложенный метод поправок прогнозируемых целевых переменных превосходит по точности как модели (18), так и модели (19) практически при любом из рассматриваемых окон данных. Исключение составляет только среднеквадратическая реализованная ошибка по модели для окна наблюдений = 100, которая в результате проведенных имитаций оказалась незначительно меньше ошибки, полученной согласно предложенной модели .

По всем целевым переменным и рассматриваемым методам точность предсказания растет с увеличением числа наблюдений и при достаточно длинном окне данных различия в среднеквадратической реализованной ошибке прогноза можно считать несущественными. Однако при анализе временных рядов макроэкономических процессов практически всегда приходится работать в условиях недостатка статистических данных. Как известно при моделировании таких данных слишком длинное окно способствует получению таких же неточных прогнозов, как и слишком короткое. Вследствие этого зачастую при анализе макроэкономических процессов возникают условия ограниченной статистики где применение предлагаемых поправок позволяет ощутимо сократить ошибку прогноза.

Далее перейдем к эмпирическому тестированию метода поправок с учетом функциональной связи моделируемых целевых переменных. Рассмотрим простейшее трехфакторное макроэкономическое уравнение: индекс ВВП равен произведению индекса дефлятора ВВП на индекс реального ВВП. Для тестирования разработанных методов была собрана поквартальная статистика по США для данных индикаторов, начиная с Q1.1947 и заканчивая Q3.2016. Таким образом набор статистических данных для проведения эмпирического эксперимента составляет 279 наблюдений. Базовая система моделей представляется в виде авторегрессии четвертого порядка как показано ниже:

I pt = b 10 + b 11 I p ( t - 1 ) + b 12 I p ( t - 2 ) + b 13 I p ( t - 3 ) + b 14 I p ( t - 4 ) , ‘ I qt = ^Ь 20 ^{+ Ь} 21 I q ( t - 1 ) ^{+ Ь} 22 I q ( t - 2 ) ^{+ Ь} 23 I q ( t - 3 ) ^{+ Ь} 24 I q ( t - 4 ) ,        (20)

I pqt = ^Ь 30 ^{+ Ь} 31 1 pq ( t - 1 ) ^{+ Ь} 32 I pq ( t - 2 ) ^{+ Ь} 33 I pq ( t - 3 ) ^{+ Ь} 34 I pq ( t - 4 ) ^.

Также добавим к сравнению модели рассматриваемых трех целевых переменных с участием всех экзогенных переменных системы (20). Таким образом получим в некотором роде эквивалент приведенной формы системы одновременных линейных уравнений.

I pt = b10 + 2bj, (t-i) + 2 <М, (t-j) + 2 d 1iIpq (t - k ), i=1                  j=1

1 Iqt = b20 + 2 b2iIp (t-i) + 2 C 2iIq (t-j) + 2 d 2 iIpq (t - k ) -i=1                   j=1

~

I pqt

= b 30 + 2 ^b3 i I p ( t - i ) + 2 ^c3i I q ( t - j ) + 2 d 3i I pq ( t - k ) .

i =1                   j =1

В таблице 2 приведена среднеквадратическая реализованная ошибка прогноза по моделям (20), (21) и моделям с поправками согласно предлагаемому методу, рассчитанным по собранной базе статистических данных.

Таблица 2. Сравнение анализируемых методов, эмпирический эксперимент, функциональная зависимость

Ip ________ ^д ______ Ipq Ip _____lq_____ ^pq Ip ______ Iq _____ ^pq

20	0.9705	0.1103	0.9757	0.9123	0.1064	0.9702	2.4943	0.3209	2.4845
30	0.8295	0.0857	0.8598	0.7985	0.0837	0.8362	1.2493	0.1734	1.3475
40	0.7695	0.0775	0.8373	0.7444	0.0769	0.7971	1.0735	0.1281	1.1849
50	0.6878	0.0779	0.7502	0.6592	0.0779	0.7181	0.9584	0.1032	1.0215
60	0.6662	0.0792	0.7364	0.6341	0.0791	0.7009	0.8775	0.0951	0.9421
70	0.6654	0.0837	0.7683	0.6443	0.0828	0.7217	0.9275	0.0957	1.0054
80	0.6562	0.0887	0.7718	0.6481	0.0887	0.7199	0.8932	0.0988	0.9639
90	0.6516	0.0866	0.7941	0.6461	0.0867	0.7388	0.9257	0.0989	0.9981
100	0.5814	0.0776	0.6822	0.5694	0.0792	0.6537	0.8594	0.1081	0.8257
110	0.5294	0.0577	0.6628	0.5247	0.0581	0.6242	0.6032	0.0701	0.7112
120	0.5324	0.0511	0.6626	0.5208	0.0521	0.6256	0.5933	0.0588	0.7183

Как видно из таблицы 2, предложенный метод поправок прогнозируемых целевых переменных в подавляющем числе случаев превосходит по точности как модели (20), так и модели (21). Исключением в данном случае являются только среднеквадратические реализованные ошибки по модели    для окон наблюдений =90,  = 100,  =110 и

= 120, которые в результате проведенного эмпирического тестирования оказалась незначительно меньше ошибки, полученной согласно предложенной модели .

Далее перейдем к тестированию предлагаемых методов поправок получаемых прогнозов в случае, когда рассматриваемые целевые переменные связаны не функциональной, а корреляционной зависимостью. Начнем с проведения имитационного эксперимента. Пусть моделируются две целевые переменные и с помощью однофакторной линейной регрессионной модели, а именно:

К = b 10 + b ll x lt , y 2 1 = ^b20 + b 21 x 2 1 ^.

Причем моделируемые целевые переменные связаны некоторой корреляционной зависимостью = + + . Для машинной генерации эндогенных и экзогенных переменных данной системы воспользуемся методом генерации коррелированных нормально распределенных случайных величин. Во-первых, определим истинную

дисперсионно-ковариационную матрицу x x2 y1 y2 x1 1 0.1 0.15 0.1 Z = X 2 0.1 1 0.1 0.15 y1 0.15 0.1 1 0.9 y2 0.1 0.15 0.9 1 посредством которой задаются взаимосвязи между экзогенными и эндогенными переменными системы. Далее введем вектор-столбец независимых, идентично распределенных переменных    × , которые подчиняются нормальному закону распределения с нулевой средней и единичной дисперсией, что подразумевает, что

E ( ZZ T ) = I m .

После чего будем генерировать переменные х_{г t} , х_{2 1} , у _іt и у ₂₁ с помощью разложения Холецкого истинной дисперсионно-ковариационной матрицы 2.

x i t = S [ 1, ^ ] Z t

X 2t = S [2,•] Zt ylt = S[3,•]Zt ,                               (23)

У 21 = S [4,•] Zt где 2 = SST, S[i,.j - i-ая строчка нижней треугольной матрицы S.

Таким образом для каждого наблюдения t получим участвующие в рассматриваемой системе уравнений переменные, которые имеют истинную дисперсионно-ковариационную матрицу 2. По аналогии с предыдущим имитационным экспериментом описанные модели тестировались на окнах данных различной длины (п) и сравнивались по показателю среднеквадратической реализованной ошибки прогноза, для расчета каждой из которых использовалось по 10 000 имитаций. Исходя из этого, полученные в результате эксперимента данные можно рассматривать в качестве основания для того, чтобы сделать состоятельные выводы относительно эффективности работы предлагаемых методов.

В таблице 3 представлена среднеквадратическая реализованная ошибка прогноза для моделей (23), а также для моделей с учетом предложенных поправок и для моделей с учетом всех объясняющих переменных системы, приведенных ниже:

~ ylt = c10 + c11 x\t + c12x21,

~ y 21 = c 20

⁺ c 2i x i t + c 22 x 2 1 .

Для проведения поправок будем использовать две функции правдоподобия. Поправки _. и _. получаются посредством максимизации следующей функции правдоподобия:

• (1)                 (2)              (1)(

LH = *1 (yn+1 ) T2 (yn+1 ) Yi yn+1 yn+1 , а поправки . и . вычисляются с помощью максимизации функции правдоподобия, представленной ниже:

• ^{(1)          (}2 H-ofl/²) ⁽¹⁾

5

1.7458

1.7253

1.4577

1.4812

1.4985

1.4371

3.3691

3.2243

6

1.5144

1.5095

1.3197

1.3378

1.3465

1.3142

2.2871

2.2294

7

1.3914

1.3867

1.2512

1.2597

1.2736

1.2387

1.8487

1.8112

8

1.3371

1.3074

1.2136

1.2288

1.2324

1.2136

1.6348

1.6468

9

1.2675

1.2454

1.1714

1.1728

1.1877

1.1601

1.5057

1.4979

10

1.2128

1.2222

1.1281

1.1504

1.1413

1.1379

1.4051

1.4161

15

1.1376

1.1253

1.0859

1.0872

1.0949

1.0808

1.2343

1.2253

20

1.0684

1.0813

1.0394

1.0485

1.0446

1.0438

1.1325

1.1389

50

0.9996

1.0116

0.9887

0.9982

0.9904

0.9976

1.0158

1.0235

LH T1 yn+1   ^2 yn+1 Фі yn+1 yn+1 .

Отличием функций правдоподобия (25) и (26) является то, что в случае (25) строится регрессия для ( ) с фактором ( ) , а для функции правдоподобия (26) наоборот – используется уравнение регрессии для ( ) с ( ) в качестве объясняющей переменной.

Таблица 3. Сравнение анализируемых методов, имитационный эксперимент, корреляционная зависимость ....

Как видно из таблицы 3, предлагаемый метод поправок во всех рассматриваемых случаях работает лучше, чем традиционные модели и модели с участием всех экзогенных факторов системы. При достаточно большом числе наблюдений разница в точности прогнозирования между анализируемыми подходами минимальна, однако при моделировании временных рядов макроэкономических процессов такая ситуация встречается крайне редко, из чего можно сделать вывод о наличии определенной практической значимости предлагаемых подходов.

Модель . , которая опирается на линию регрессии от , показывает более высокую точность прогноза, чем модель . , использующая уравнение регрессии от . Аналогичный вывод можно сделать и о моделях . - . , где поправки с использованием регрессии от работают лучше для прогнозирования переменной .

Среднеквадратические реализованные ошибки прогноза по сравниваемым моделям демонстрируют схожую нисходящую динамику с уменьшающейся разницей по мере увеличения числа наблюдений в окне данных. Таким образом, исходя из проведенного анализа, есть основания утверждать, что является целесообразным, применять рекомендацию, высказанную выше, о том, что в процессе выбора между получившимися корректировками, рекомендуется выбрать ту, при проведении которой корректируемая целевая переменная моделируется через остальные с помощью линии регрессии.

модели, а именно:

y t = b io + ^Ьіі У і ( t - 1 ) , У 2 t = ^b20 + b 21 У 2 ( t - 2 ) ^.

Здесь отметим, что во избежание высокой степени мультиколлинеарности между лаговыми переменными системы (27) и, как следствие, малой информативности поправок при такой структуре уравнений переменная моделируется с помощью лага -2, а не -1. По аналогии с предыдущими экспериментами описанные модели тестировались на окнах данных различной длины ( ) и сравнивались по показателю среднеквадратической реализованной ошибки прогноза, для расчета каждой из которых использовались дневные данные по рассматриваемым фондовым индексам США за период с 05.10.2012 по 05.10.2017.

В таблице 4 представлена среднеквадратическая реализованная ошибка прогноза для моделей (27), а также для моделей с учетом предложенных поправок и для моделей с учетом всех объясняющих переменных системы, приведенных ниже:

~ ylt = c10 + c11y1( t-1) + c12 y 2( t-2),

~ y 21 = c 20 + c 21y1( t-1) + c 22 y 2( t - 2)-

По аналогии с предыдущим имитационным экспериментом для проведения поправок будем использовать две функции правдоподобия. Поправки . и . получаются посредством максимизации функции правдоподобия (25), а поправки . и . вычисляются с помощью максимизации функции правдоподобия (26).

Таблица 4. Сравнение анализируемых методов, эмпирический эксперимент, корреляционная зависимость п Уі У2     Уі.1_____У2 .1     Уі.2_____У2 .2      Уі______У2

5	1.0316	1.1901	0.8787	0.9914	0.8813	0.9731	1.6726	1.8255
6	0.9159	1.0409	0.7846	0.8589	0.7929	0.8524	1.3907	1.4832
7	0.8381	0.9439	0.7569	0.8232	0.7564	0.8107	1.1868	1.2695
8	0.7646	0.8501	0.7084	0.7645	0.7134	0.7627	1.0383	1.1243
9	0.7322	0.8268	0.6798	0.7433	0.6853	0.7418	0.9737	1.0591
10	0.6858	0.7825	0.6585	0.7182	0.6603	0.7157	0.8821	0.9529
15	0.6429	0.7235	0.6191	0.6723	0.6196	0.6701	0.7339	0.7872
20	0.6161	0.6753	0.5999	0.6424	0.6019	0.6436	0.6789	0.7301
30	0.5799	0.6476	0.5731	0.6209	0.5756	0.6208	0.6133	0.6643
50	0.5763	0.6267	0.5679	0.6111	0.5717	0.6118	0.5968	0.6406

Анализируя результаты, представленные в таблице 4, можно заключить, что предлагаемый метод поправок дает меньшую по сравнению с другими методами среднеквадратическую реализованную ошибку прогноза при любом из рассматриваемых числе наблюдений. Однако в сравнении с таблицей 3, где превосходство модели . над _. и модели _. над _. было однозначно, при моделировании эмпирических данных в отдельных случаях модель _. работает несколько лучше, чем модель . (при числе наблюдений 71=7), а также _. является более точной, чем _. (при числе наблюдений 71 = 20 и 71 = 50). Во всех остальных случаях наблюдается аналогичная таблице 3 ситуация.

Также можно отчетливо проследить, что предлагаемый метод дает существенное улучшение качества прогноза по сравнению с моделями (27) и (28), особенно в условиях короткого окна данных. Модели (28) являются явными аутсайдерами по точности получаемых прогнозов, что явно заметно в условиях малого числа наблюдений. Причиной этому служит тот факт, что каждая из этих моделей включает в себя все экзогенные переменные системы регрессионных уравнений, что требует оценки большего числа параметров, чем для моделей (27). Вследствие этого возрастает общая неопределенность относительно прогнозируемого значения, поскольку она учитывает неопределенность в оценке каждого из имеющихся параметров регрессионного уравнения. Естественно, данный эффект нивелируется при увеличении числа наблюдений. Однако, несмотря на то, что при достаточно длинном окне данных разница в точности прогнозирования между анализируемыми подходами минимальна, данный метод представляется актуальным в силу того, что при моделировании временных рядов макроэкономических процессов ситуация достаточности статистических данных встречается крайне редко, а даже в тех ситуациях, когда это так, длинное окно данных не дает улучшения точности прогноза, а наоборот достаточно часто происходит ее падение.

Модель Уі. 1, которая опирается на линию регрессии у1t от у2t, в среднем показывает более высокую точность прогноза, чем модель ^. 2, использующая уравнение регрессии у 21 от у 11. Аналогичный вывод можно сделать и о моделях у 2. г -у2.2, где поправки с использованием регрессии у21 от угt показывают более высокую эффективность для прогнозирования целевой переменной . Однако по сравнению с имитационным экспериментом в данном случае различие между этими противопоставляемыми моделями не так велико. Тем не менее в среднем можно заключить, что модель . работает лучше модели у 1.2, а модель у 2.2 — лучше модели у 2. i• Таким образом эмпирический эксперимент  также,  как и  имитационный, подтверждает целесообразность высказанной выше рекомендации относительно того, что в процессе  выбора между  получившимися корректировками, рекомендуется выбрать ту, при проведении которой корректируемая целевая переменная моделируется через остальные с помощью линии регрессии.

• 5.    ЗАКЛЮЧЕНИЕ

В работе представлен метод учета функциональных и корреляционных взаимосвязей между моделируемыми макроэкономическими индикаторами. Проведенные имитационные и эмпирические эксперименты показывают на достаточно простых примерах практическую пользу от предлагаемых методов поправок прогнозов при одновременном моделировании временных рядов макроэкономических процессов функционально или корреляционно зависящих друг от друга. При проведении таких поправок получаемые прогнозы являются согласованными между собой, а не «оторванными» выходами каждой из несвязанных между собой моделей, что неминуемо сказывается на их качестве. В общем и целом, разработанные методы дают значимое улучшение качества прогнозов по сравнению с регрессионными уравнениями, моделирующими каждый макроэкономический процесс по отдельности, а также работают лучше моделей, включающих все экзогенные переменные рассматриваемой системы уравнений. Данный положительный эффект достигается за счет использования незадействованной в традиционных моделях информации о виде функциональной или корреляционной зависимости между прогнозируемыми целевыми переменными. В силу того, что существует возможность функционально связать большинство макроэкономических индикаторов между собой предлагаемый в данной научной работе метод поправок получаемых прогнозов может считаться актуальным для комплексного прогнозирования макроэкономических систем.