Повышение точности работы метода измерения плотностей и границы раздела между слоями двухслойной жидкости в резервуаре

Задача измерения плотностей двухслойной жидкости и положения границы раздела между слоями является распространенной в различных практических приложениях.

В работе [1] предложен метод измерения плотностей и границы раздела между слоями двухслойной жидкости в резервуаре, главным достоинством которого является применение всего двух датчиков давления для измерения как плотностей слоев, так и положения границы раздела между слоями. Одним из недостатков предложенного способа является отсутствие фильтрации шумов применяемых датчиков давления.

В процессе измерения в данных с датчиков будет неизбежно присутствовать шум, вызванный различными факторами. Для того чтобы повысить точность измерения, предлагается использовать фильтрацию с помощью рекуррентного алгоритма, основанного на методе фильтра Калмана [2].

1. Начальные условия

Рассмотрим резервуар с двухслойной жидко- стью, которая занимает весь объем резервуара. Примем, что начало координат находится в верхней граничной плоскости резервуара (рис. 1).

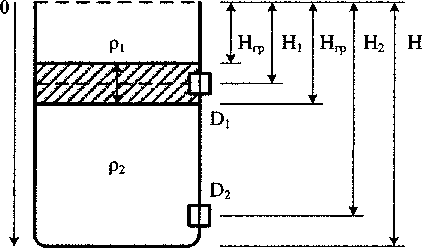
Рис. 1. Резервуар с двумя датчиками давления

На резервуаре закреплены два датчика давления В_г и £)₂.Датчик давления В₂ расположен у дна резервуара, а датчик В_г находится на уровне некоторого среднего значения, относительно которого колеблется положение границы раздела между слоями.

За счет колебаний границы раздела между слоями датчик D_T попеременно оказывается то в верхнем слое и будет измеряться плотность p_v то в нижнем слое и будет измеряться плотность р₂.

На рис. 1 заштрихованная полоса обозначает интервал, в котором колеблется граница раздела между слоями. Согласно [1] плотности слоев и положение границы раздела будут определяться

следующими зависимостями:

зШг-НгУ                            v 7

_ Р20Нг-Рг*Ратм                          zo\

S(P2-Pi) '

анализа погрешностей [1] следует, что наибольшее влияние шум в данных с датчиков

Ар Из

вие этих шумов переменные р_г и р₂ зависели бы от к строго линейно. К шумам процесса отнесем все факторы, вызывающие отклонения хода изменения величин pi и р₂ от линейности. Поскольку характеристики этих шумов могут быть описаны лишь приближенно, примем, что шумы ш_1к и to_{2 k} имеют нормальное распределение с нулевыми математическими ожиданиями и среднеквадратичными отклонениями a_Pt, о_рг соответственно.

давления будет оказывать на погрешность определения плотностей слоев, в то время как точность определения положения границы раздела будет в большей степени зависеть от разности плотностей. В связи с этим возникает задача восстановления с

< P2,fc = P2,fc — 0 ' p2,fr + 0 ' to2,fr.

максимальной точностью плотностей слоев р_г и р₂ по данным с датчиков давления D_T и D₂.

Определим связи между переменными и за

Запишем ее в матричном виде:

Pl.fc+l 2 -1 0 0 ■ ’ Pi.fc " Pl.k 1 0 0 0 Pi.fc-i Рг,к+1 0 0 2 -1 Pi.fc . Р2,к . 0 0 1 0 ■ .P2,fc-1. tol.fr-0 ш2,к

о

пишем их в матричном виде:

А = УА ' Pi + А™;

Р₂ = 9^2 ~ НО ■ р2 + дН_г ■ р! + Р^,

отсюда

Pi -Р^ = уА ■ Pi + о ■ р₂;

Р₂ -Ра™ = дн_г • Pi + д(н_г - н_г) • р₂;

Pi - Ам] ₌ \g^Hi °    1ГР11

A-A™J № PCA-HJJW'

Введем обозначения: "Pl,fc+1"

А+1 —

Эта матричная запись справедлива в условиях

отсутствия шумов.

времени к+1; г2

2. Стохастические уравнения, описывающие

Л =

- вектор состояния в момент

ход технологического процесса

Для использования фильтра Каймана необходимо описать технологический процесс в виде стохастических дифференциальных или разностных уравнений, которые дают представление о нормальном ходе процесса. Отклонение от нормального хода процесса принимается случайным и

1 0

-0

-1 0

0 0

0 ■

-1

0 -

матрица эволюции

Х_к в отсутствие шумов;

Хк =

времени к;

Ргл-1.

- вектор состояния в момент

считается шумом процесса.

Будем считать, что типичное поведение параметров pt и р2 - медленное изменение, приближенно линейное во времени. Так как измерения

Wk =

«1Л 0 w2,k . о .

- вектор шума процесса.

производятся один раз в единицу дискретного времени к, наши уравнения естественно записать

В результате система (7) в матричном виде запишется следующим образом:

как разностные (дискретные), используя подход,

Xk+1=A-Xk + Wk.

предложенный в работе [3] для определения плот

ности и уровня однослойной жидкости:

Р1Л ~ Р1,к-1 — Ар1 _ „

„    _ п _      Р1Л+1 — zPl,k

Р1Л+1 Р1Л ~ аР1

-Р1Л-1 + Ш1А (Р2,/с ~ Р2Л-1 = ^Р2 1рг,к+1 — Ргл = АРг ~P2,k-l + Ы2,Л.

^ Р2Л+1 — 2р2 к

3. Уравнения, описывающие процесс измерения

Уравнение (9) - это уравнение процесса. Добавим к нему уравнение измерения, полученное из выражения (4) с использованием введенного вектора Х_к и с учетом шумов измерения:

Здесь индекс к нумерует дискретные моменты

времени; ш_1к и to_2ik — шумы процесса. В отсутст-

+о • Ргл + о • p2,k-i;

(Ю)

Ак - Ам] _ рАО 0   01

Лл-^J b^oyC^-HJoJ Ak + tVvk3

Введем следующие обозначения:

[ р    р 1

^г1,к ^гатм

„    □   - вектор результатов изме-

*2,к   *атм!

где Ор10 и Ор20- априорные значения дисперсий плотностей в начальный момент времени.

С ростом числа итераций к матрица ковариации вектора состояния Р_к быстро стабилизируется и

рения;

дн_г о о

_днго д(Н2-Нг)

- матрица наблю

дения;

rVik]

V_k ⁼ [v₂ kJ ” ^вектоР ^шУ^ма измерения.

В итоге система (10) в матричном виде запишется следующим образом:

Y_k = C-X_k + V_k.                       (12)

В результате получим динамическую стохастическую систему:

№+1 = А " Х_к + W_k;

I Y_k = C-X_k + V_k.

перестает зависеть от своего начального значения.

Задав начальные значения, можно осуществить прогнозирование ожидаемых значений матриц фильтра Калмана. Прогнозируем вектор состояния Х_к по Х_к-1 и ковариационную матрицу Р_к по P_k-v

Х_к+1=А-Х_к,                      (19)

P_k+i=A-P_k-A^T + Q,               (20)

где О - ковариационная матрица шума процесса,

которая характеризует влияние шумов друг на друга, то есть характеризует отклонение процесса от линейности. Эта матрица определяется следующим образом:

Q = M\WkWkT\ =

4. Синтез фильтра Калмана

На первом этапе синтеза фильтра зададим на

чальные значения параметров вектора состояния

Х_о и матрицы ковариации Р_о.

Хо —

Р1,0 Р1,0 Рг.о

Р2,О

- оценка вектора состояния в начальный момент

времени.

Этот вектор состоит из величин р10 и р20, вычисленных согласно формулам (1) и (2) по данным датчиков давления в начальный (нулевой)

момент времени, то есть

„        ^>1,0-*^*атм.

Р1,о = ——;                        (15)

_ Р2,0“^1,0

Р2-° ~ д(н2-НгУ                              <

Примем, что в начальный момент времени в резервуаре находились оба слоя жидкости, граница раздела хотя бы 1 раз перешла через верхний датчик давления.

Определимся с начальными значениями элементов ковариационной матрицы ошибок оценивания вектора состояния в начальный момент времени. В общем виде ковариационная матрица Р_о определяется выражением [2]:

Р₀=М [(Х_о - А)(А - Х₀)^Г],         (17)

где Х_о - истинное значение вектора состояния в начальный момент времени. Элементами вектора Х_а — Х_о будут являться среднеквадратические отклонения погрешностей определения плотностей слоев в начальный момент времени. Тогда ковариационная матрица Р_о запишется в виде

41л

. 0

0 о

о

0 0 °Р2,к о

О' о о о

где <Тр_1#с и Ор_2к - дисперсии погрешностей определения плотности слоев. Так как шумы процесса

w_ljfc и со₂,кнеза^висимы, ^все недиагональные элементы матрицы Q равны нулю.

Следующим этапом синтеза фильтра является корректировка прогнозируемых значений. Для этого необходимо вычислить оптимальную матрицу усиления фильтра (коэффициент Калмана)[2]:

U_k=P_k-C^T АС-Р_к-С^т A-RY\ (22) где R - ковариационная матрица шума измерения, которая характеризует влияние погрешностей датчиков давления друг на друга, г тз            0 1

R = M[I4V] = М ₂,           (23)

L и O2J где о^ и о2 - дисперсии погрешностей датчиков давления.

Обновим оценку для среднего значения вектора состояния по новым результатам измерения Y_k:

X_k=X_k + U_kAY_k-C-X_k]          (24)

и оценку для матрицы ковариации:

Р_к-Р_к-и_к-С-Р_к.                (25)

В процессе работы фильтра с увеличением числа итераций к матрицы Р_к и U_k стабилизируются, что говорит о сходимости фильтра Калмана. Установившиеся значения этих матриц будут зависеть от матриц R, Q и А.

• 5.    Численное моделирование работы алгоритма и фильтра Калмана

Предложенный алгоритм повышения точности работы метода измерения плотностей слоев и границы раздела между слоями двухслойной жидкости был смоделирован в пакете Matlab 7.7.0 с начальными условиями:

• -    высота резервуара 500 см;

• -    первый датчик погружен на глубину 250 см;

• -    второй датчик погружен на глубину 350 см;

• -    граница раздела находится на глубине 250 см;

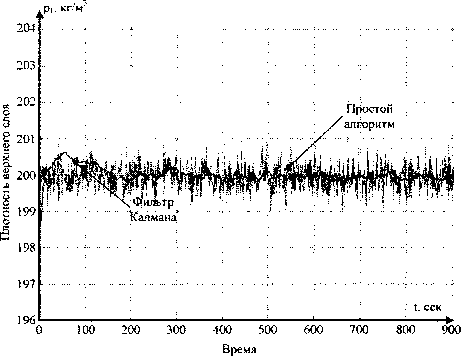
Рис. 2. Плотность pt верхнего слоя

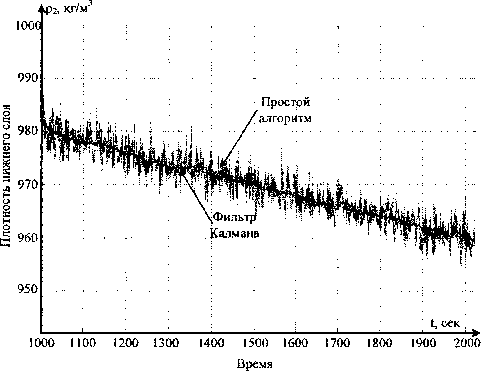
Рис. 3. Плотность р2 нижнего слоя

Время

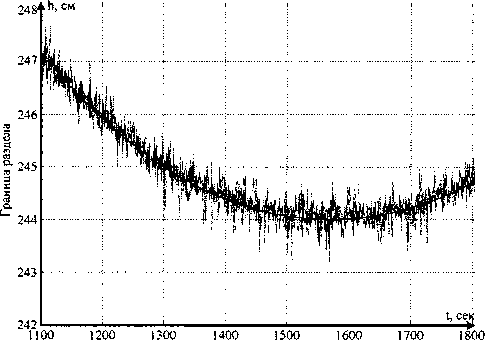
Рис. 4. Положение границы раздела Н,_р между слоями

• -    плотность верхнего слоя 200 кг/м³ и остается постоянной;

• -    плотность нижнего слоя 1000 кг/м³ и за время моделирования уменьшается до 900 кг/м³;

• -    время моделирования 5000 с;

• - предполагалось, что погрешности датчиков представляют собой белый шум с амплитудой 2 % от предельного значения показания датчиков;

  -положение границы раздела слоев задавалось выражением

Н^ = 10(sin(0,003t) + 0,4cos(0,004t)), где /- время, с.

На рис. 2-4 представлены графики результатов моделирования, где сплошные линии - это заданные функции изменения параметров.

По результатам моделирования определили, что - СКО плотности pj верхнего слоя ар =1,59 кт/м '; - СКО плотности pj верхнего слоя с использованием фильтра Калмана оР1 = 0,46 кг/м3;

• -    СКО плотности р₂ нижнего слоя Ор₂⁼ 10,71 кг/м⁵;

• -    СКО плотности р₂ нижнего слоя с исполь

зованием фильтра Калмана о£2 =2,97 кг/м3;

• - СКО положения границы раздела с_н,^ = 6,29 10”³ м;

• - СКО положения границы раздела, рассчитанное по отфильтрованным плотностям р_г и р2, <^ =6,24 10³м.

Значения СКО сг_Р1, o_Pz и о_н^ рассчитывались по простому методу, предложенному в [1]. Для всех параметров смещение математического ожидания отсутствует.

Результаты проведенного моделирования показывают, что применение рекуррентного алгоритма, основанного на фильтре Калмана, приводит к существенному повышению точности измерения.

Заключение

Предложен алгоритм повышения точности работы метода измерения плотностей слоев и границы раздела между слоями двухслойной жидкости, основанный на применении фильтрации Калмана. Приведены результаты моделирования предложенного алгоритма, которые подтверждают его работоспособность и более высокую точность по сравнению с расчетами этих параметров прямым методом.