Повышение точности весовых расчетов крыльев

Для всех проектов летательных аппаратов (ЛА) одной из главных характеристик является взлетная масса. Исторически в авиационной технической литературе наряду с термином «масса» используется термин «вес». Масса конструкции и вес конструкции применяются как разнозначные термины в связи с устойчивыми традициями в авиационно-технической литературе и необходимостью использования таких понятий, как «весовые формулы», «весовое проектирование», которые по своей сути связаны с расчетами и прогнозированием массы конструкций. В теории проектирования ЛА весовым расчетам уделяется большое внимание [1]. Взлетная масса самолета определяется из так называемого уравнения существования [2]:

m ц + m эксл

¹ - m к - m су - m ТС - m об.упр

где m 0 – взлетная масса самолета, m ц – масса целевой нагрузки, m эксл –су м марная масса экипажа и служебной нагрузки, m к , m су , m _ТС , m об.упр – относительная масса конструкции, силовой установки, топливной системы и оборудования и управления.

Примерные значения относительных масс магистрального пассажирского самолета имеют следующие величины: m К =0,3, m ТС =0,25, m су ,=0,15, m об =0,1, при этом на долю полезной нагрузки (пассажиры, грузы и т.п.) остается 20% от взлетной массы. Отсюда следует, что уменьшение доли массы конструкции от взлетной на 1% позволяет перебросить этот «процент» на полезную нагрузку, которая станет 21% в нашем примере. Следовательно, величина полезной

(платной) нагрузки может быть увеличена на 5%. Из уравнения (1) хорошо видно, что даже небольшие изменения относительных масс частей ЛА вызывают существенное изменение его взлетной характеристики m 0 .

До последнего времени в качестве основного инструмента прогнозирования массы конструкции используются весовые формулы [3]. Весовые формулы отдельных частей конструкций – крыла, фюзеляжа и оперения – строятся, как правило, с использованием простейших физических представлений об их силовой работе с использованием балочной математической модели, которая дополняется поправочными коэффициентами из статистической обработки весовых данных по ранее построенным самолетам. Для ЛА с традиционными внешними формами весовые формулы дают достаточно высокую точность, хотя известный специалист по весовым расчетам В.М. Шейнин [1] рекомендует для страховки использовать несколько весовых формул различных авторов, крайние значения отбрасывать, а оставшиеся – осреднять. В случае проектирования ЛА с новыми аэродинамическими формами и компоновками, а также в случае разработки ЛА очень больших или очень малых размеров по сравнению со среднестатистическими, возникает необходимость разработки новых методов весовых расчетов. В [4] предложена новая структура весовых формул, основу которых составляет коэффициент силового фактора, который учитывает особенности внешней формы конструкции, её силовой схемы и распределения нагрузки через высокоточное математическое моделирование авиационных конструкций с использованием метода конечных элементов (МКЭ) и численных методов аэродинамики. В частности, для оценки абсолютной и относительной массы крыльев эти формулы имеют следующий вид:

m кр = =СК n р m0gVS а m кр

m * = ^ С _к n р g^S = £ с К n р g m₀   а         а

,

где m _кр - масса крыла, _а - удельная прочность материала, φ – коэффициент полной массы, n р – перегрузка, p 0 – удельная нагрузка на крыло, S – площадь крыла. Особенности вычисления коэффициента силового фактора С к для крыльев обсуждаются в [5].

Одной из существенных проблем в прогнозировании массы конструкции с использованием соотношений (2) и (3) является правильный учет распределения аэродинамической нагрузки по крылу. Дело в том, что под нагрузкой крылья деформируются, и могут изменяться углы атаки поточных сечений, что приводит к изменению распределения нагрузки по размаху. Это хорошо известный эффект, особенно для стреловидных крыльев [6]. Однако на ранних стадиях проектирования не известна конструкция крыла, и поэтому нагрузки считаются в предположении его абсолютной жесткости. Для преодоления этой неопределенности в [7] предлагается методика, которая заключается в следующем:

• 1.    В ограничения внешних размеров крыла с учетом объемов занятых механизацией, шассий-ными вырезами и т.п. вписывается тело переменной плотности с модулем упругости и предельными напряжениями, линейно завися-щими от плотности.

• 2.    Рассчитываются аэродинамические нагрузки в предположении абсолютной жесткости крыла.

• 3.    По специальному алгоритму оптимизируется распределение плотностей и определяется деформированное состояние крыла.

• 4.    Рассчитываются аэродинамические нагрузки с учетом деформации крыла, и повторяется оптимизация распределения материала.

Расчеты показывают, что данный алгоритм сходится за 3-4 итерации пересчета аэродинамических нагрузок. При этом пробные расчеты показали также, что учет деформаций крыльев приводит к существенному изменению циркуляции и соответственному распределению нагрузки по размаху [7].

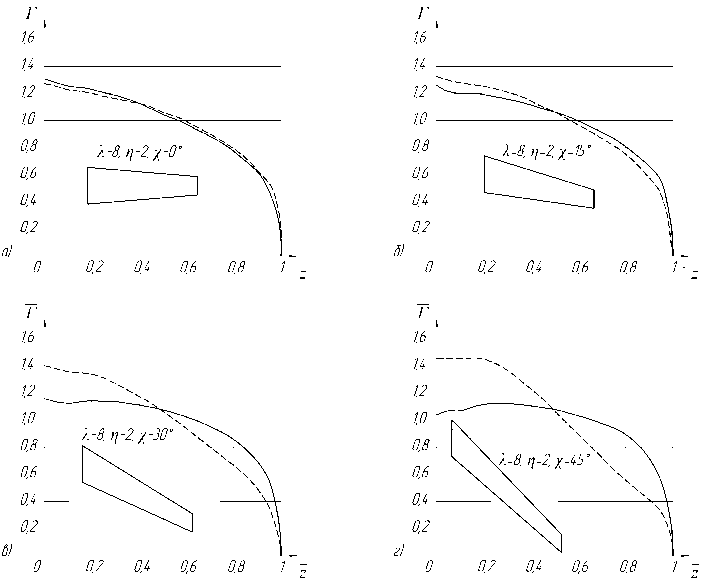
-----------жесткое крыло

--------деформоробонное крыло

Рис. 1. Распределение аэродинамической нагрузки по размаху

С целью обеспечения достоверности определения деформаций крыла с использованием новой оптимизационной модели исследованы факторы, влияющие на результаты прогноза. Установлено, что наиболее существенным является уровень достижимых напряжений в обшивке, минимально допустимая жесткость крыла в концевых сечениях и особенности использования трехмерных конечных элементов в данной задаче [8]. В данной работе выполнено исследование влияния на массу конструкции крыла зависимости распределения аэродинамической нагрузки от его деформаций. В качестве объекта исследования выбрано характерное для современных магистральных самолетов крыло с удлинением λ=8, сужением η=2 и относительной строительной высотой c =10% при различных углах стреловидности. На рис. 1 показано распределение аэродинамической нагрузки по размаху крыла. Для расчетов напряженно-деформированного состояния крыла использовалась система NASTRAN. Оптимизация распределения материала в трехмерной модели крыла выполнялась с использованием специальной программы [9]. Расчеты циркуляции выполнены по программе APAME [10].

Для оценки весовой эффективности рассматриваемых крыльев использовался безразмерный коэффициент силового фактора [7, 8]. В рассматриваемом комплексе программ этот коэффициент вычислялся следующим образом: на каждой итерации распределения плотности материала в 3D-модели крыла вычислялась размерная интегральная характеристика – силовой фактор G .

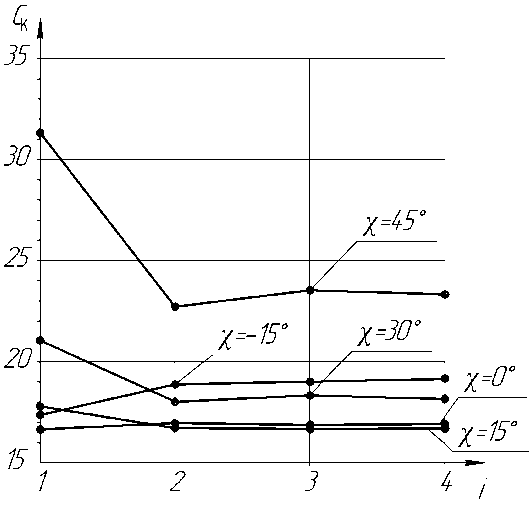
Рис. 2. Изменение коэффициента силового фактора по итерациям

G = ∫ σ ^экв dV = ∑ ⁿ σ ^экв V _i V                  i = 1

,

где σ ^экв – эквивалентное напряжение, V – объем тела (материала конструкции), V i – объем конечного элемента, n – число элементов.

Безразмерный коэффициент силового фактора вычислялся как отношение силового фактора к характерной нагрузке и размеру конструкции. В соответствии с [7, 8] в качестве характерной нагрузки выбиралась подъемная сила крыла Y , а в качестве характерного размера - S .

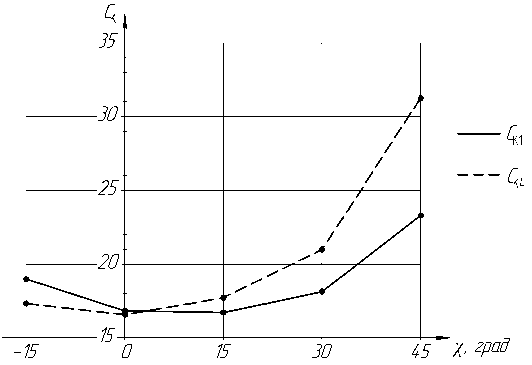
Рис. 3. Коэффициент силового фактора

С к = _Y ^G _S

.

Изменение этого коэффициента по итерациям перерасчета нагрузок показано на рис. 2 для крыльев с различной стреловидностью.

На рис. 2 значения коэффициента силового фактора С к на первой итерации соответствуют распределению аэродинамической нагрузки в предположении абсолютно жесткой конструкции крыла, а на 3 и последующих итерациях, когда процесс сходится, эти значения соответствуют распределению нагрузки на деформированном крыле. Для удобства анализа на рис. 3 показана зависимость коэффициента силового фактора от стреловидности крыла для абсолютно жесткой конструкции С к1 ( χ ) и для деформированной конструкции близкой к оптимальной (на четвертой итерации) - С к4 ( χ ).На рис. 2 и 3 отрицательные значения χ соответствуют обратной стреловидности.

В области положительных стреловидностей полученный характер изменения Ск1 от угла стреловидности для абсолютно жесткого крыла хорошо согласуется с весовой формулой для крыльев дозвуковых самолетов [3, стр. 131], в которой стреловидность учитывается множителем cos-1,5χ. Деформированное крыло имеет значительно меньшую величину Ск , что свидетельствует о наличии существенных резервов массы силовых элементов конструкции крыла. Этот резерв для крыла со стреловидностью 30о имеет величину порядка 14% и для 45о – 25%. Специальные расчеты для крыла с геометрическими характеристиками близкими к крылу самолета Ту-204 со стреловидностью по передней кромке -30о показали резерв массы силовых элементов порядка 17%. Физически этот эффект объясняется очень просто: отрицательные изменения углов атаки поточных сечений стреловидного крыла, вызванные изгибом, преобладают над положительным изменением углов , вызванных кручением крыла. В выполненных расчетах аэродинамическая нагрузка прикладывалась по ¼ хорд, что вызыва- ет практически максимальное «положительное» закручивание крыла. Оно проявилось только в несколько большем коэффициенте Ск4 при χ=0о. В случае обратной стреловидности наблюдается вполне ожидаемое увеличение Ск за счет приращения углов атаки концевых сечений крыла. На рис. 4 показано отношение Ск4/Ск1 в зависимости от угла стреловидности. Оно показывает отношение массы силовых элементов крыла, спроектированного по нагрузкам, рассчитанным с учетом его деформаций к соответствующей массе крыла, спроектированного по нагрузкам для абсолютно жесткой конструкции.

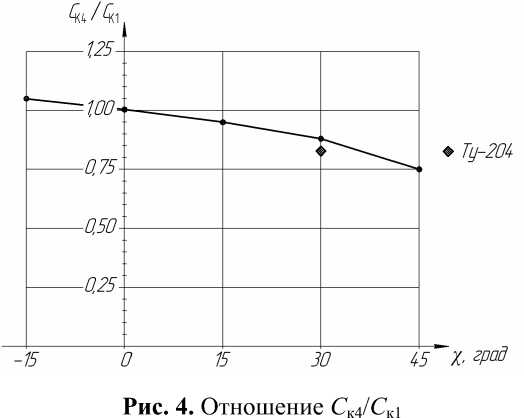
Выводы:

• 1.    Деформации крыла оказывают существенное влияние на распределение аэродинамической нагрузки, которое необходимо учитывать на ранних стадиях проектирования.

• 2.    В случае положительной стреловидности учет перераспределения нагрузки указывает на значительные резервы массы силовых элементов конструкции. В частности для крыла со стреловидностью 45^о выигрыш в массе составляет 25%.

• 3.    Полученные зависимости С к4 / С к1 ( χ ) могут быть использованы для корректировки весовых формул крыльев с учетом того обстоятельства, что в конструкциях крыла доля силовых элементов составляет примерно половину его общей массы.

Работа выполнена с поддержкой по ФЦП «Научно и научно-педагогические кадры инновационной России» на 2009-2013 годы, государственный контракт №14.740.11.0126 от 13.09.2010 г.