Power Aware Reliable Virtual Machine Coordinator Election Algorithm in Service Oriented Systems

Published Online September 2013 in MECS

Cloud Computing is an emerging paradigm that aims at streamlining on-demand provisioning of software, hardware and data as a service. Providing end user with flexible and scalable services accessible through the internet [1].

However this computing paradigm is challenged in many aspects such as power usage, availability, reliability and especially security. Hence a central controller existence is crucial in order to coordinate Virtual Machines (VM) located on physical resources. VMs should communicate to one another in majority of cases to make their jobs finished. To control these communications and activities of the systems, one of these VM must be set as a coordinator (leader) to achieve more performance [2].

A coordinator could be initiator of an activity (e. g.

reconstruction of lost Token in a Token Ring network), recognizer of the deadlock or failures, the root of a spanning tree [3] and it also needed in applications such as video conferencing and multiplayer games. Coordinator algorithms have lots of usages in different research areas such as Ad Hoc networks [4, 5].

Leader election algorithms are useful in various areas such as distributed systems for load balancing and to keep resource replicas consistent [6].

Power management in datacenters is a huge challenge since datacenters can consume 10 to 100 more energy per square than typical office building [7]. They can even consume as much electricity as a city [8]. Power consumption in these datacenters is because of computation processing, disk storage, network and cooling systems [9]. More utilization of server resources incurs higher power consumption.

As a VM elected for coordinator responsibility of a network, more resources would be utilized. Therefore if a server is in its low utilization and is going to be turned off, additional load should not go toward it which is VM coordinator responsibility. This issue is taken into account in this article to have a Power Aware Reliable Message efficient Coordinator Election Algorithm (PARMCEA) which could tolerate multiple VM failures.

The paper outline is as follows. Related work is discussed in section 2. Problem formulation is introduced in section 3 and section 4 is devoted to proposed algorithm. After that algorithm’s mathematical analyzing will be presented in section 5. Next simulation results will be shown in section 6. Finally section 7 concludes this paper.

• II.    Related Work

Coordinator Election area welcomed wide ranges of algorithms with the passing of time. Bully [10] and Ring [11]are two classic ones that are referred to in many papers. Bully algorithm whose network topology is used in this paper launches election when processes find coordinator crashed. In the first step of election, these processes send Election messages to the processes with an upper process number than themselves. Then when processes receive Election labeled message, they will respond by an OK message. However if no process responds, the sender would introduce itself as the new coordinator to the system by sending a Coordinator message to them. If process P2 replies the sender, P2 will send another Election message in the system by using the previous procedure. These steps continue until no other process with an upper number than the sender process exists or any other OK messages from the upper number processes didn’t receive to informer.

Uniform self–stabilizing distributed algorithm which elects the process of least ID as coordinator. Let denote n with network’s process number is proposed in [12]. The algorithm’s contribution is based on stabilization and it constructs a breadth first search (BFS) tree rooted at coordinator within O (n). An algorithm based on star graph is proposed by Shi et al. [13] which uses tournament scheme based on the recursive structure of the star graph. A star graph Sn of dimension n is decomposed into n substars Sn-1 of dimension n-1. Coordinator election is launching in Sn by the elected coordinators in Sn-1. The message passing complexity in each step is from O ( Vn ), but the whole algorithm is from O (n).

Bakhshi et al. [14] presented a probabilistic election algorithm with average message complexity O (n) for anonymous, unidirectional asynchronous bounded expected delay network. Every node is in one of the following states: idle, active, passive or leader which idle is the default one. The algorithm passes messages among the nodes and will change the idle ones to passive or active. Coordinator will be the active node that initially created and sent message in the network. Stabilization and fault-tolerant elections in systems with static crash failures is studied by Delporte-Gallet [15]. They considered stabilization in the form of selfstabilization and pseudo-stabilization, so they tried to have election algorithms with these types of characteristics. Five systems are assumed in their paper. The base one has arbitrary slow or loosely communication links and then appropriate election algorithms are proposed for each of them.

Election algorithms are also vital in mobile ad hoc networks, so many algorithms are proposed in this area such as (Derhab et al. 2008), (Boukerche et al. 2006) and (Melit et al. 2011).

Considerable amount of work have been done in the area of coordinator election but few are able to apply on cloud computing with power optimization consideration. For increasing paper readability, Table I presents key symbol used thorough this paper along with their definitions.

• III.    Problem Formulation

The most powerful VM should be elected as coordinator to make communications and processing more efficient. Coordinator Workload (CW), VM utilization and server utilization are calculated by (1) , (2) and (3) respectively.

wk

Ui,j,new =wj +CWj

Ui,new = ^n=1Ui,j,new

It should be noted if a VM have no dependency on others, then 2 would be zero.

Some servers in a cloud system are in their low utilization, so they can be turned off after migrating their VMs to other servers with reasonable utilization, hence less power will be used. However, by assigning coordinator responsibility to VMs in low utilized server, additional workload will be added to the server which makes the management center not to be able to turn it off. Therefore power usage will be taken into account if a refinement on VMs qualified to participate in election is done. Most of the time lowest possible utilization (U l ) and highest one (U h ) are considered in a datacenter. Four situations could be existed due to these thresholds.

• 1.    Moderate Workload : Some VMs don’t violent

thresholds. Therefore set of VMs able to participate in the election achieves according to below equations.

S={S i |U i,new h &&U i >U l }                   (4)

• VM = [VM j |VM j placed on S i &S i e S}               (5)

• 2.    Low Workload:All servers are already in lower utilization than U l . In this case, first of all High Utilized Server (HUS) is selected by (6). Then election will be held among VMs identified by (7).

• 3.    High Workload:All servers are in higher utility than

• 4.    Unbalanced Workload:Some servers are over utilized whether others are underutilized. If coordinator workload added to some over utilized servers, failure possibility will be increased. Equation 10 selects The Highest Low Utilized Server (HLUS) and the following one determines the set of VMs in the elect\ion.

HUS = {S i |VS_kU_k< U i }                             (6)

VM = [VM j |VM j is placed on HUS}                (7)

Uh. In the same way as previous condition, first of all Low Utilized Server (LUS) will be selected by (8) and then an election will be held among VMs identified by (9).

LUS = {S i lVS k U k > U i }                              (8)

VM = [VM j IvM j is placed on LUS }                (9)

HLUS = {S i I VS_kU i > U_k I I (U_k > U i &&U_k >

Uh)

VM = [VMj IVMj is placed on HLUS }

If k 1 virtual machines remain in VM set, the problem of coordinator election will be solved by (12).

Coordinator = Max ( U™1PCj)

• IV. Proposed Algorithm

It is considered that each VM placed in any servers has full information about others whether in the same or different server, so they can easily communicate (like the one Bully is based on). PARMCEA has following specifications.

• •    K coordinator alternatives (A 1 , A 2 , A 3 ,_,A_k,) are considered which replaced to coordinator respectively at any time it crashed. So whenever coordinator VM faults

• •    It’ll be replaced by its alternatives to avoid having a down system. Therefore makes the system more reliable.

• •    T is denoted with the number of VMs received Election messages and didn’t reply back to it.

• •    The replying back Election message might not sent by VM or received to informer although VMs are available. In this case the message will be sent to them once more to gain more powerful algorithm since the reason might be message loosing during network transition or 100% CPU usage in the time.

After refinement procedure, the algorithm elects coordinator and its K alternatives by these six steps following:

• •    First of all, the algorithm will be launched by a random VM.

• •    Then the VM sends Election message to K (number of alternatives) VMs with upper number than themselves .

• •    After that, the available VM send their number to election informer VMs.

• •    Next, the election message will be sent again to any VMs which haven’t replied (T ones totally). The messages also will be sent to the next T upper number VM to place each of them respectively as alternative if any of those T VMs do not respond. It means that if 1 ,VM₂, VM 3 ,... ,VM_t) are formed VM which failed to respond to the election procedure, the coordinator message will be sent to them and the next upper T number ones.

• •    The most upper number VM are elected as coordinator with the next K upper ones as its alternatives.

• •    Finally, the informer propagates coordinator message into network to announce new coordinator and its K alternatives.

Table 1: Notation and Definition

Symbol	Definition
MN	Message Number passed thorough election procedure
CAN	Coordinator Alternative number in cloud
SPN	Site j Process Number
CC	Communication Cost
PT	Processing Time
ECT	Election Process Consuming Time
FCC	Failure Communication Cost
PC j	Processing Capacity of VM j
w j , w i	Work load of VM j and S i
n	Number of VMs
n i	Number of VMs placed on server i
t c, j	Communicating time between any VM to VM j
p j , d	Processing time required for VM j to coordinate each request.
U l , U h	The lowest and highest utilization of each server
U i, j , new	Utilization of VM j placed on S i after electing as coordinator
U i , U i, new	Server i utilization before and after taking coordinator responsibility by one of its VMs
CW	The Workload due to coordinator responsibility
α	Communication time between two VMs
β	Consuming time to compare two numbers by a VM
λ j	Dependency coefficient of VM j

PARMCEA pseudo code when there isn’t any coordinator in network isshownin Fig. 1, Fig 2, Fig 3, and Fig 4. The algorithm in Fig. 1 calls others respectively. Fig. 2 shows estimation pseudo code of each VM as a coordinator. VMs will be qualified to nominate for coordinator role if they don’t violate the low and high utilization thresholds.

Fig. 3 is the pseudo code of refinement procedure and Fig 4 shows election algorithm. As it is clear, refinement is applying by the first function. If all VMs that received election messages respond to the informer, the election will be held; otherwise previous functions will be done

.PARMCEA Algorithm()

U= New utility estimation^, ns, X, w, s, p);

Refinement(U);

Election Algorithm(VM, K);

• Fig.1:    PARMCEA steps

Array New Utility Estimation(n c , n s , Array λ, w, t, p)

Array CW, U new

For all VM j {

CW j = 0;

For all VM k {

IfX k !=0 {

CW += XW (t cj + P jd )

U i, j, new = W j + CW j }

} return U

• Fig.2:    Estimating VMs as coordinator

VM Refinement(Array VM Utilizations)

If no server S i violates thresholds

VM = all VMs;

Else if all are lower than U L

VM = VMs from servers with highest utilization;

Else if all upper than U H

VM = VMs from server with lowest utilization;

Else

VM = VMs from highest underutilized serve.

Return VM;

• Fig.3:    Refinement procedure pseudo code

Void Election Algorithm(Starter VM, K Alternatives)

M= K upper VMs;

Send election message M;

Wait for replying back;

If (all K VM are already replied)

{

Select coordinators;

Select alternatives;

Inform all processes;

}

Else

{

T = set of VMs didn’t reply;

Index = 0;

While (number of elected alternatives < K)

{

M= set of T most next upper number;

Send election message to M and T;

Wait for replying back;

If (index = 0)

Select coordinator;

T = set of VMs didn’t reply;

Index ++;

}

}

• Fig.4:    PARMCEA pseudo code

• V.    Mathematical Analyze

• 5.1    Message Complexity Analyzing

• 5.2    Time Complexity Analyzing

One of the most important characteristics of an algorithm is the number of messages it should exchangein order to elect a coordinator, which is highly important in the high traffic networks.

Messages Number (MN) is subject to the VMs Number (VMN) and Coordinator Alternatives Number (CAN). Hence, the total site’s messages number during election at the best case achieves by (13).

MN = 2 * CAN+VMN - 1                   (13)

However, when response disability by VM in the site is considered, MN will be increased. Therefore, the worst case of the algorithm is calculated by (14). It should be mentioned this number is achieved when all the VM in cloud are crashed except informer, so there is no need to inform the others about the elected coordinator, which is the informer itself.

MN = CAN + 2 * (CAN) * ( VMN/CAN) = CAN + 2 * VMN                                     (14)

In the best case, Communication Cost (CC) of this algorithm is calculated by (15). However, it’s Processing Time (PT) is equal to zero since all the alternatives are responding.

CC = 2 * CAN *a + VMN                     (15)

Therefore, the election time is equal to communication time. (13) will be changed to (16) in the worst case of the algorithm. Algorithm PT and the entire Election Consuming Time (ECT) are also calculated by (17) and (18).

CC = (2 * VMN + CAN) * a                   (16)

PT = (VMN/ CAN ) * в                        (17)

ECT = (2 * VMN + CAN) * a + (VMN/ CAN ) * в

As it is obvious this algorithm is from Ο (VMN) and Ω (VMN).

• VI.    Simulation Analyze

The algorithm is implemented and tested by real life gained data. Unbalanced workload and moderate workload cases is examined and denoted with test 2 and test 1 respectively in the text For each test two cases considered by setting λ=1/2 (case 1) and 0 (case 2). Moreover to demonstrate the effectiveness of the proposed algorithm in power reduction, same algorithm with no power awareness is also implemented and tested by the simulator. Algorithm 3 is considered to be Bully algorithm in order to make a comparison. Hence Al2Ca1Te2 refers to no power considered algorithm with λ=1/2 in unbalanced server utilization environment. The number of alternative existed in the system should be set by provider due to reliability and VMs number in the system (more alternative increases reliability although some VMs don’t have long lifetime). For each test, server’s utilization selected randomly in the related range and it is also assumed that jobs are interactive type which doesn’t demand much of a CPU capacity. Moreover the lowest and highest utility threshold is set to be 20% and 70%.

Fig.1 illustrates the result of the comparing algorithm 1 in all 4 existed cases in 16 time periods of system life cycle when two faults are occurred at the first time period and 10 one at any other. 400 servers are in the system and it is obvious that Al1Ca1Te1 exchanges fewer message in comparison to other situation because of omitting VMs placed on servers that violent the lowest and highest utilization thresholds (in comparison to Al1Ca2Te1) and also VMs independency possibility. The sudden increase in number of message in algorithm is due to launching new election after all coordinator alternatives failure. Fig.2 is shown the simulation results of algorithm 2 on the same situation as previous simulation for algorithm 1. Same result is also gained although reduction of messages in comparison to previous test is clear. Next test is devoted to compare algorithm 1 and algorithm 2. As it is clear by Fig. 3 power aware characteristic of algorithm 1 made number of VMs participated in election far fewer which leaded to fewer message exchanging number thorough election.

Table 2: Comparison among algorithms in conditions of case 1 of test 1

Fault Number	VM in Cloud	VM in Al1	VM in Al2	Al1Ca1Te1	Al2Ca1Te1	Al3Ca1Te1
0	9383	918	6185	1009	6276	5330204
2	9381	916	6183	916	6183	6094251
12	9371	906	6173	906	6173	6580811
32	9351	886	6153	886	6153	7048379
42	9341	876	6143	876	6143	5173799
52	9331	880	6143	971	6234	5873410
62	9321	870	6133	870	6133	5479562
72	9311	860	6123	860	6123	6599494

It also infers from the figure that more servers in system cause more differentiate message passing between these algorithms. Test 4 result is shown in Table 2. Algorithm 1, 2 and 3 reactions in case 1 of test

1 where 400 servers and 9383 VMs are existed in the system are illustrated thorough 8 time periods of system life cycle. The reduction of exchanged message by proposed algorithm is wide clear in this table.

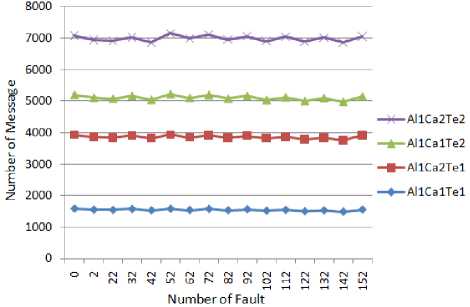
Fig.5: Algorithm 1 behavior comparison in four cases

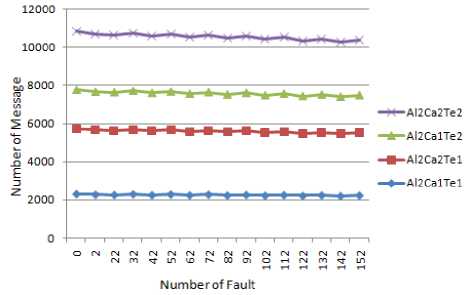
Fig.6: Algorithm 2 behavior comparison in four cases

• VII.    Conclusion

Due to high power usage of datacenters green algorithms should implemented. Many VMs should communicate to ea each other to make their jobs done. A power aware VMs coordinator election algorithm proposed in this paper.

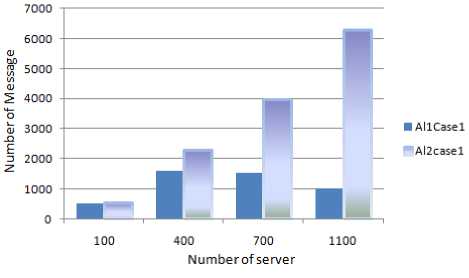
Fig.7: Comparison between algorithm 1 and algorithm 2

First of all a refinement procedure applied on the VMs allowed to participate in election, and then election was launched. Mathematical analyze shows that the algorithm is from θ(VMN) and the simulation result proved the efficiency of algorithm in avoiding more load on overloaded or under loaded coordinator responsibility to give them the chance to go to sleep mode or increasing their reliability. Algorithm compared to Bully and a dramatic reduction in number of exchanged message to elect the coordinator was achieved.