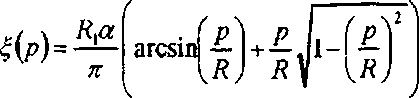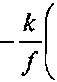Практический алгоритм расчета фокусаторов в линию с использованием криволинейных координат

Для широкого спектра технологических задач требуется фокусировка лазерного излучения в заданную линию. Для фокусировки в линию были созданы дифракционные фазовые оптические элементы, названные фокусаторами [1-4]. Расчет фокусаторов проводится в приближении геометрической оптики. Ввиду сложности решения обратной задачи фокусировки, фазовые функции фокусаторов получены только для случаев фокусировки в простые линии, такие как отрезок, кольцо, полукольцо. При фокусировке в более сложные кривые расчет фазы фо-кусатора является неординарной задачей, включаю-щсй решение сложных нелинейных уравнений.

В данной работе рассмотрен метод расчета фокусаторов в криволинейной системе координат, согласованной с видом фокальной кривой. Предлагаемые криволинейные координаты существенно упрощают расчет и позволяют предложить простой численный алгоритм расчета фокусаторов для произвольной фокальной линии.

Для описания задач, возникающих при расчете фокусаторов [1-4], рассмотрим предварительно стандартную процедуру расчета фазовой функции фокусатора в линию для пучка с распределением интенсивности 70 (u),u 6 G , где u=(«,v) - декартовы координаты в плоскости фокусатора (при z=0), G -апертура фокусатора. Фокальную линию в плоскости фокусировки т=/ определим параметрическим уравнением

х(#)=(Шг(г)ке[о,/.]

где £ - натуральный параметр, а распределение линейной плотности энергии вдоль линии фокусировки - функцией /(£),£ е [о, 7.].

Фазовая функция фокусатора в параксиальном приближении имеет вид [1-4]:

Hu) = -yr + ^(u) (D где

Функция ^(u) в (2) описывает лучевое соответствие между' точками (и у) апертуры фокусатора G и точками фокальной кривой. В работах [1-4] показано, что в каждую точку (у\'(^),К(^)) кривой приходят лучи с линии Г(£) на фокусаторе, называемой слоем. В параксиальном приближении слоями являются прямые, перпендикулярные линии фокусировки. Таким образом уравнение слоя Г(с) имеет вид u^+v^-p^

и является базовым уравнением для определения функции ^и) в (2). Функция р(б) в (3) является расстоянием от начала координат до слоя Г(^) и определяется из условия формирования заданного распределения линейной плотности 7(£).£ ^е К^] вдоль линии фокусировки. Конкретный вид функции р(£) определяется из уравнения сохранения светового потока: х

|70(и^2и = |7(^77                  (4)

(r(o).rk)) о где область интегрирования (г(о),Г(^)) соответствует части апертуры G фокусатора, заключенной между начальным слоем Г(0), являющимся касательной к апертуре и текущим слоем Г(£).

Таким образом стандартный алгоритм расчета фазовой функции фокусатора имеет вид:

• 1.    Расчет функции р(Д) из уравнения (4)

• 2.    Расчет функции $(и) из уравнения (3)

• 3.    Расчет фазовой функции по формуле (1)

Аналитический расчет фазовой функции фокусатора возможен лишь для простейших линий фокусировки таких как отрезок и окружность. В общем случае пункты 1). 2) алгоритма являются сложными вычислительными задачами, состоящими в решении нелинейных уравнений. При этом пункт (2) требует решения нелинейного уравнения для каждой точки и апертуры фокусатора. Выполнение пункта 3) алгоритма также основано на операции двумерного численного интегрирования.

Расчет фокусатора существенно упрощается при использовании следующей криволинейной системы координат:

^.Ур^)^-!^ di di

^=р^я.ф

Система координат (5) связана со слоями на фокусаторе и выражает координаты (мд) через координату i, определяющую слой 1 (£). содержащий данную точку и координату I. определяющую положение точки на слое. Отметим, что координата ( является расстоянием от точки слоя (»((),/),v(O,z)), являющейся точкой пересечения слоя и нормали к слою, до теку щей точки слоя. В последующем изложении мы ограничимся рассмотрением практически важного случая фокусировки в кривую радиальных пучков;

/„(uH^+v2)^^/?             (б)

где R - радиус апертуры фокусатора.

Для радиально-симметричных пучков закон сохранения светового потока (4) в координатах (50 может быть представлен в компактной дифференциальной форме:

V^2 -р2«)

Фё) J/o^ti+z’^-/^      (7)

-^-pV)

Поскольку интеграл в (7) обращается в ноль при p^\p^=±R, то уравнение (7) следует решать относительно функции ^р). Согласно (7), расчет ^р') состоит в решении дифференциального уравнения первого порядка, разрешенного относительно производной и может быть проведен с использованием стандартного метода Рунге-Кутта. Далее вычисление р(^) состоит в обращении гладкой однозначной функции $р\

Основное преимущество в использовании координат (50 состоит в возможности прямого вычисления фазы фокусатора без расчета функции 5(и), состоящего в решении нелинейного уравнения для каждой точки и апертуры фокусатора. Действительно, из уравнений (1), (5) несложно получить частные производные функции ^(и) (2) в переменных (50 в виде:

^5     / L d£ d^

d^ - d^ \ f

\Ш^+„(£\Ш1.

[ dE d^ ' d^

d<‘

^Д=*Г^) , , rfel^l’

^         d^            dq _

at

Уравнения (8). (9) позволяют представить фазовую функцию фокусатора в переменных (c.t) в виде:

♦уГ^г^)-^)^!,*

ращению полученного решения и одномерному интегрированию функции р(5).

Операция изготовления фотошаблона фокусатора на литографе или лазерном фотопостроителе предполагает использование декартовых или полярных координат. Согласно (10), при фиксированном значении 5 фазовая функция вдоль слоя соответствует суперпозиции фазовых функций линзы и призмы. Это позволяет интерпретировать фокусатор как набор цилиндрических линз и призм, ориентированных вдоль слоев Г(5) При этом для точек и е г(5) фазовая функция имеет вид:

v'pV-^T+^tgVvY^*^ (11)

где

c(5)=-7f Л^-

J о

Согласно (11), для расчета фазовой функции (10) в декартовых координатах (a,v) достаточно построить систему из N слоев (3) по функции р(5). При этом система слоев Г(с „) n=l,N определит разбиение апертуры фокусатора на N сегментов G;. Далее, для вычисления фазы фокусатора в точке и достаточно найти сегмент G;, содержащий данную точку и воспользоваться формулой (11). Отмстим, что поиск сегмента G„ содержащего данную точку и, сводится к тривиальным операциям определения положения точки относительно прямых.

Проведенный анализ структуры фазы фокусатора вдоль слоев позволяет предложить следующий простой алгоритм расчета фазовой функции фокусатора:

• 1.    Расчет функции р(5) из уравнения (7).

• 2.    Переход к декартовым (или полярным) координатам с введением дискретной системы слоев и последующим расчетом фазы в сегментах по формуле (11).

В качестве примера для разработанного метода рассмотрим расчет фокусатора плоского пучка круглого сечения радиуса R в дугу⁷ окружности с постоянной линейной плотностью. Параметрическое уравнение дуги имеет вид:

J X (5) = R_x cos((5 - R_xa 1 2)/ A,) 1Г(5) = ^ sin((5-/?,«/2)//?,)

где R^ - радиус дуги, a - угловой размер дуги.

Из закона сохранения светового потока (7) несложно получить функцию 5(р) в виде:

^»^k-

Л ^ d? J

-^p^               (io)

J о

Согласно уравнениям (7), (10) расчет фазы фокусатора в переменных (Ц) сводится к решению дифференциального уравнения первого порядка, об

Подставляя (12) в (5), (10) получим фазовую функцию фокусатора в дугу в виде:

^О = "Т7(/?2Й)^/2)

/•^ +^p№n

Простой вид полученной фазы (14) демонстрирует достоинство криволинейной системы (5). Расчет фазы (14) сводится к выполнению только двух простых численных операций обращения функции (13) и ее одномерного интегрирования,

На рис.1 приведено полутоновое изображение фазовой функции фокусатора, рассчитанной как дополнение к линзе, для следующих параметров Х=0.63мкм,/=500мм, /?=5мм, Л]=1.25мм, cfhQ. Для расчета фазы (14) в декартовых координатах быта построена система из 200 слоев по функции p(ff найденной из уравнения (13) с последующим использованием формулы (11). Полутоновое распределение интенсивности, формируемое фокусатором на рис.1, приведено на рис.2 и демонстрирует работоспособность разработанного метода.

Рис. 1. Фазовая функция фокусатора для фокусировки в дугу окружности

Рис. 2. Распределение интенсивности в плоскости фокусировки, формируемое фокусатором на рис 1

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 96-15-96026)