Практическое применение методов проектирования характеристик элементов на основе функционально-градиентных композиционных материалов

Практическое рассмотрение материалов как функционально-градиентных дает широкие возможности проектирования распределения характеристик в соответствии с их функциональным назначением. Конструирование структуры в соответствии с широким спектром воздействий на слои элемента в процессе эксплуатации дает рациональное и эффективное использование возможностей материала.

В ряде работ даны решения задач плоского напряженного состояния для тел с известной неоднородностью упругих свойств, в том числе при наличии анизотропии [1; 2; 3]. Интересно рассмотрение обратной задачи, состоящей в определении упругих параметров, необходимых для реализации желательного распределения напряжений. При этом мы ограничимся неоднородными изотропными телами, поскольку, двух упругих параметров таких тел достаточно для достижения цели.

Для напряжений, заданных в условиях удовлетворяющих уравнениям равновесия, уравнение неразрывности деформации, с учетом преобразований, принимает вид дифференциального с частными производными

(o_y — vo_x) ^-^ — 2(1 + v)T_xy^д-^- +

У     ^ dx^{2    v}      ' ^xy дхду

• — ^^^^^д^*^^

• ^{x       у} dy²        дх дх        dy dy

«V2 ((^x — Oy)) = 0, где а = а (х, у) – коэффициент деформации (коэффициент податливости), являющийся функцией координат. Он представляет собой величину, обратную модулю упругости

Е = Е (х, у), т. е.

1 a = - , E ’

а коэффициент поперечных деформаций v будем полагать не зависящим от координат.

Решение этого уравнения даст функциональную зависимость коэффициента деформации, а, следовательно, и модуля упругости от координат, при которой осуществимо заданное напряженное состояние.

Решения данной задачи для случая простого изгиба консольного прямоугольного элемента единичной толщины (рисунок 1)

Ox = kxffy); Oy = 0,

где k – некоторый коэффициент пропорциональности; х – расстояние от конца консоли (места приложения силы Q ) до рассматриваемого поперечного сечения пластинки; f(ƞ) – функция, характеризующая распределение напряжений σ х по высоте сечения (одинаковая для всех сечений); ƞ = у/b .

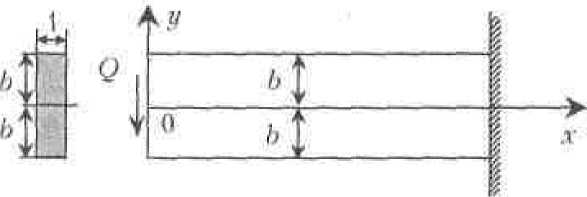
Рис. 1. Расчетная схема консольной пластинки строится на предположении распределения напряжений.

Функция распределения нормальных напряжений σ х должна удовлетворять также следующему условию:

£_b ° x ydy = M, где М = Qx – изгибающий момент в сечении.

Исходя из конструктивно-технологических соображений установим, что а = а(у), v= const , т. е. упругие свойства вдоль оси х неизменны. При этих условиях уравнение неразрывности деформаций, становясь обыкновенным дифференциальным, принимает вид d²a  ^df^) da    d²f(rf)

dq2      d^ dq      d^2

или

d2

[af (гУ] = 0

dr/2

Решение этого уравнения выражается формулой

af (Г = С1Г + С2

Условия задания функции f(^) таковы, что при ^=0  f(^)=0. Поэтому С2=0 и а = С1 у^ или если С=1/С1, то

c  f(r)>

E = С--- r

Отношение модуля упругости E=E(y) волокна, имеющего безразмерную ординату ^=у/Ь к модулю упругости Е о осевого волокна, определится, соответственно, следующим образом:

E

E 0

f(Г) Г Г 1

r   lf(r)l4=0

Таким образом, все решение

определяется заданием характера статически возможных напряжений ox, т.е. функции f(^). Полученный расчетом закон распределения модуля упругости Е по сечению образца может быть реализован различными, например технологическими, способами (таблица 1) [4].

С целью изучения реализации принципов получения функционально-градиентных материалов была исследована работа и распределение свойств по высоте поперечного сечения изгибаемых образцов, изготовленных по методике крупнопористого бетона. Исследования проводились на стандартных образцах размером 40х40х160 мм с основной крупнопористой структурой, полученной из гранитного щебня с полимерным связующим, и дополнительной двухсторонней комбинированной пропиткой (полимерной с растянутой стороны и цементной в сжатой зоне).

При выборе материала для пропитки исходили из следующих предположений: композиты могут применяться в условиях воздействия агрессивных сред, материал пропитки должен обеспечивать хорошее сцепление с рабочей арматурой и надежную работу при изгибе изделия. Учитывая, что материал растянутой зоны должен защищать композит и арматуру от воздействия агрессивной среды, иметь хорошую растяжимость и не допускать выдергивания стержней арматуры, материалом для нее выбран состав на основе эпоксидной смолы. Цементная пропитка верхних слоев обеспечивает хорошую сопротивляемость сжимающим усилиям и, что немаловажно, обходится гораздо дешевле эпоксидного состава. В растянутой зоне в дополнение к полимерной составляющей размещалась стальная арматура.

В результате пропитки упругие характеристики изменяются по высоте элемента и зависят, в основном, от двух факторов: свойств материалов, составляющих определенный слой конструкции, и их объемного содержания. Например, модуль упругости Е км композиционного материала можно оценить по следующей формуле:

^км = E1Y1 + E2Y2

где Е 1 , Е 2 – модули упругости основной структуры и пропитки соответственно; γ 1 , γ 2 – их объемное содержание.

Таблица 1

Изменение несущей способности изгибаемых элементов для возможных вариантов распределение модуля упругости при соответствующем напряженном состоянии

№п/п	Характер распределения функции f(ƞ)	Эпюра распределения σ	Эпюра распределения Е/Е 0	S' ?
1	ƞ	1,5 1.5	1 1	1
2	. я smy^	1,2 3	0,64	1,22
			------- 1
		1 .2 3	0,64
3	. 2 Sin —^7/	0,87 -----/ 1	0,42	1,42
		1 4—
		0,87	0.42
4	е’-1 ' l-e-’J	1,72	1.72	1,5
		1.72	1.72

Проведенные испытания крупнопористых образцов позволили оценить изменение упруго-прочностных характеристик по сечению образца в зависимости от свойств материалов и наполнения пустот базовой структуры. При постоянном модуле упругости Е 1 модуль упругости пропитки Е 2 зависит от вида пропиточного состава и степени заполнения пустот (рис. 2).

Таким образом, с учетом арматуры формула для оценки модуля упругости материала в растянутой зоне элемента будет выглядеть следующим образом:

E = Е1У1 + E2Y2 + Esys

где E s , ? s - модуль упругости арматуры и ее объемное содержание соответственно.

На примере образцов с крупнопористой структурой оценивалась эффективность применения метода расчета распределения свойств при заданном напряженном состоянии. В результате испытаний на изгиб крупнопористого композита были определены относительные деформации слоев материала. При известном модуле упругости на сжатой и растянутой гранях мы получаем представление о напряженном состоянии изгибаемого элемента. Опытным путем определены напряжения в характерных точках сечения.

Используя предварительные экспериментальные данные, имеем возможность задать функцию распределения напряжений, аппроксимируемую кривой показательной функции

/(Л) = 6^-1

Так, для случая с неармированным образцом имеем следующую функцию распределения напряжения:

( е0.75(л-0.1)

{1 — еШ-П

Подбирая последовательно функцию f(^) для каждого типа образцов, мы задаемся распределением нормальных напряжений по высоте поперечного сечения. Затем по формуле

E = С---

Л

определяем необходимое изменение модуля упругости по сечению. Данное распределение обеспечивает напряженно-деформированное состояние, которое описывается выбранной нами функцией.

Полученную кривую (линия 2 на рис. 2) распределения модуля упругости по высоте сечения неармированного образца сравниваем с опытными данными (линия 1 на рис. 2). Разница результатов находится в допустимой погрешности, и зависит, вероятно, от не совсем точного описания истинной кривой изменения по сечению величины напряжений.

Повышение несущей способности (по сравнению с крупнопористым элементом с пустотами, заполненными цементом) при расчете по приведенным выше формулам составило 1,53 раза; по экспериментальным данным – в 1,54 раза.

На основании аналитических выражений изгибаемых моментов запроектирована несущая способность образцов с различным армированием.

В процессе испытаний образцов на изгиб установлены следующие величины максимальных изгибающих моментов: для неармированных образцов – 32,52 кН×м; для изделий с одним арматурным стержнем диаметром 3мм – 41 кН×м; для балок с двумя стержнями – 56,4 кН×м; для образцов с тремя стержнями — 66 кН×м. При вычислениях получены, соответственно, следующие значения моментов: 39,2; 43,1; 47,8 и 59,4 кН×м.

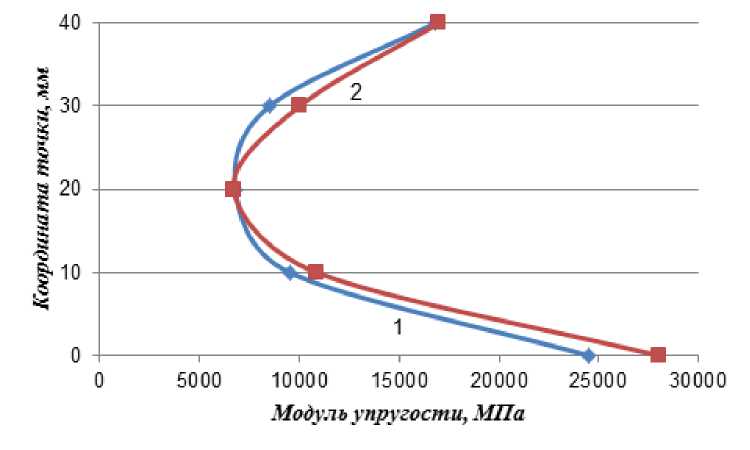
Рис. 2. Изменение модуля упругости по высоте сечения неармированного образца:

1 – опытные данные, 2 – по результатам вычислений

Таким образом, при проектировании элементов с заданным распределением напряжений, мы можем добиваться увеличения несущей способности элементов, эффективнее использовать их упруго-прочностные характеристики, что приводит к более рациональному применению этих материалов.