Правка листовых заготовок пластическим растяжением с учетом сжатия в области захватов

EDN: VYNPRV

При прокатке тонких листов могут возникать дефекты в виде потери плоскостности из-за неравномерного обжатия заготовки по ширине, причиной которого могут являться упругий прогиб валков, а также упругое сплющивание поверхности валков в зоне пятна контакта [1], что в свою очередь влияет на неравномерность зазора между валками. Взаимодействие прокатанных участков с разными коэффициентами вытяжки вызывает в листе неравномерность напряжений: сжатия в более вытянутых участках и растяжения в менее вытянутых [2, 3]. При незначительной поперечной жесткости тонких листов прокат теряет устойчивость, образуя волнообразную поверхность (рис. 1) [3].

Рис. 1. Коробление тонких листов

После разрезки листа полосы также могут наследовать дефекты формы в направлении толщины. За показатель волнистости принимают величину относительной неравномерности вытяжки при прокатке продольных участков листовой заготовки [1, 2, 3]:

д^ _ ^L max ^L min L

где L, L max , L min - длины листа (полосы), наибольшего и наименьшего участков заготовки соответственно.

Принимая во внимание гипотезу, что волнистость имеет переменную кривизну только по направлению, а по величине равномерную, как показано на рис. 1а, на основе геометрических параметров (длины дуги радиусом R, хорды l и высоты t ), можно выразить величину относительной неравномерности вытяжки продольных участков листа (полосы) [3]:

^4{ ’ ² - ⁷ (?) '

Тогда показателем волнистости будет отношение

Q) _ const при любых изменениях волнистости у каждого конкретного листа (полосы).

Подлежащую правке заготовку закрепляют концами в захватах и затем перемещением одного или обоих захватов растягивают на определенную величину относительного удлинения. Для заготовок из малоуглеродистых сталей и алюминиевых сплавов относительное удлинение находится в пределах 1-3 %. В результате правки растяжением достигается уменьшение волнистости до 1-2 мм на 1 погонный метр длины, а чтобы получить высококачественные заготовки - до 0,15-0,2 мм на 1 погонный метр [3].

При правке растяжением длины прямолинейных участков заготовки увеличиваются до длины волнистых участков, что ведет к исчезновению прогибов и заготовка становится ровной в направлении толщины. При этом относительные удлинения различных участков заготовки на кривой упрочнения вписываются в зону 5 min 5 max (рис. 2) [6].

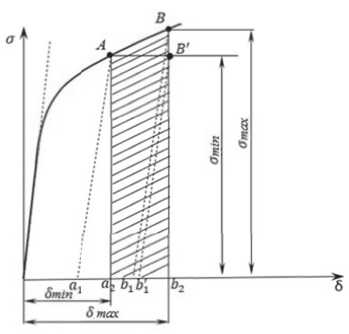
Рис. 2. Схема пружинения участков заготовки при снятии растягивающей нагрузки: а 1 а ₂ - относительная деформация укорочения наименее растянутых участков; b 1 b ₂ - относительная деформация укорочения наиболее растянутых участков; b 1 - относительная деформация А 5 _ост, компенсирующаяся появлением остаточной волнистости в менее растянутых участках ^ тах ^ min ^Д ^ ост                    ,

Е где о max, о min - напряжения в наиболее и наименее растянутых участках заготовки; E - модуль упругости металла заготовки.

При равномерном растяжении возникающие относительные поперечные деформации по длине и толщине заготовки одинаковы по абсолютной величине. Зоны заготовки под захватами не могут деформироваться по ширине, т.е. являются жесткими концами, нарушающими равномерность растяжения, что приводит к образованию треугольных зон скольжения, заштрихованных на рис. 3 [3]. Вдоль боковых сторон треугольных зон происходит интенсивное течение металла. В итоге возникают зоны затрудненной и повышенной деформации. На расстоянии (0,6 — 0,7)Ь от захватов образуются местные сужения растягиваемой заготовки, приводящие к нарушению прямолинейности силового потока и возникновению сжимающих напряжений поперек заготовки, а это, в свою очередь, может привести к потере устойчивости листа и возникновению продольной волнистости. Таким образом, допустимая величина относительного удлинения при правке растяжением тонких заготовок ограничивается потерей их устойчивости [4, 5]. Растягивающая сила определяется растягивающим напряжением σр, устанавливаемым по кривой упрочнения по заданной величине относительного удлинения:

P = Fy.

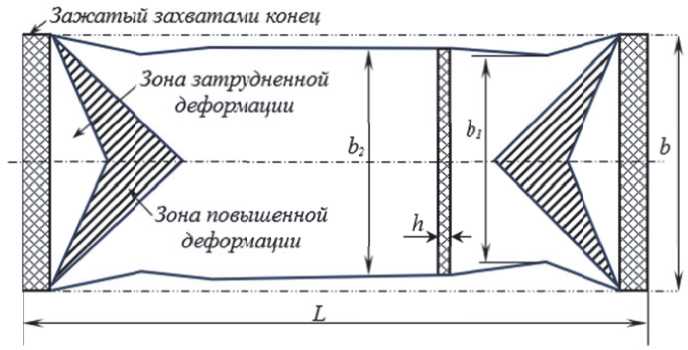
Рис. 3. Схема деформаций листовой заготовки при правке растяжением:

b, b ₁, b ₂ – соответственно исходная ширина полосы, уменьшение ширины в средней части и в зоне интенсивного течения металла в результате растяжения; h – толщина полосы

В зонах заготовки, расположенных под захватами, решается классическая задача о сжатии металла между сближающимися шероховатыми плоскостями твердых тел (захватов) [7]. Результаты объясняют присущие описываемым физическим процессам некоторые качественные особенности: явление проскальзывания вдоль поверхностей контакта захватов с заготовкой; соизмеримость нормальных упругих перемещений контактирующих тел с толщиной полосы [8]. С другой стороны, задача помогает объяснить механизм контактного взаимодействия твердых и пластически деформируемых тел. Л. Прандтлем построено предельное поле напряжений [7], которое Надаи [9] дополнил соответствующими скоростями течения. На основе анализа решения Прандтля – Надаи А.А. Ильюшиным [10] была предложена приближенная математическая модель для описания процесса течения пластических слоев.

Дальнейшее развитие эта теория получила в работах многих авторов, в том числе [11-14]. Рассмотрим частные задачи, которые приводят к общему решению правки листовых заготовок.

Задача 1. Сжатие полосы в условиях плоской деформации [15] в области:

S = {(x,y)| — h < у < h; —l^ < x < l2]

с симметричными условиями на концах в зонах захватов [16] (рис. 4).

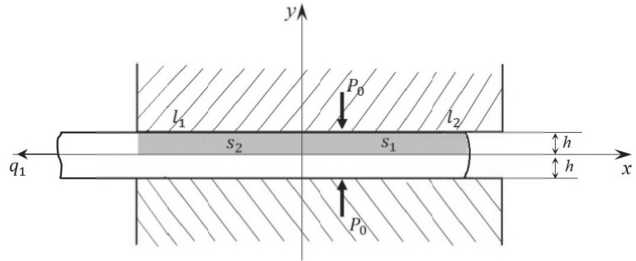
Рис. 4. К задаче о свободном растекании пластического слоя между плоскими захватами: q ₁ –растягивающая нагрузка; h – половина толщины полосы;

(– l ₁, h ); ( l ₂, h ) – координаты крайних точек захвата; l ₂= – l ₁ – симметричность условий на торцах

Постановка задачи в этом случае имеет вид системы, содержащей: уравнения квазистатического равновесия

d£^ + £o^ dx ду

д°ху I д°уу = q дх ду ’

условие пластичности

(охх ^уу) + ^^ху   ^s , (6) уравнения состояния 2os ач — aS4 = з^' (7) VXX ^ vуу   0. (8) Уравнение (7) представим в развернутом виде: 2os ^хх — о = 3V vxx> (9) 2as оуу — о = зvгVуу' (10) 2as оху — о = ЗVГVху. (11) Вычтем уравнение (10) из соотношения (9): = 2°s охх  оуу   3v \vхх vуу). (12) Найдем частное от деления уравнения (12) на (11): (0и — (охх — ^уу)   vхх — vуу    дх 0v\ ду) (13) оху        Vху     А ди dv 2\ду^ дх) Выпишем условие несжимаемости: ди dv о дх ду . (14) Добавим к задаче граничные условия: у = 0: v = 0,Оху = 0; (15) у = h\ v = —v0 = ^,оху = —TsSign -(v ■ ку), (16) где к±) - положительное направление оси Ox. Из условия (7) следует, что на контактной границе у = h существует неизвестная точка x = xp , при переходе через которую напряжение оху меняет знак, другими словами, точка x = xp попадает на линию ветвления течения. Поэтому интегрирование системы (5) будем проводить отдельно для областей:

Sr = {х\хр < х < l), S2 = [х\ — l < х < хр), S = S^ S2.

Неизвестная точка x = x_p определяется из дополнительного условия непрерывности нормального напряжения О уу .

В предположении, что искомые компоненты скорости v и v_х у есть функции, зависящие только от координаты у:

v = v(y);                                         17)

^v ху ^v ху ^(y)

получаем из уравнения несжимаемости (4) соотношение

дv(y')

и(х,у) =-----х + ^(у)                        (18)

оу где /-(у), - постоянная интегрирования.

Подставляя (18) во второе уравнение (17), получим зависимость:

^=№+^=1гд^^

у 2 ду ох 2     оу^

В последнем уравнении члены, зависящие от координаты y, принимают значения:

£^ — 0.^ = 0 дх         дул и решение отыщется в виде:

v = с±у + с2,                                     (19)

где c ₁ и c ₂ – постоянные интегрирования, которые определяются из граничных условий:

^ПР^И и |_у=0 ⁼ 0 из уравнения (19): 0 ■ с₁ + с₂ — 0 находим с₂ = 0;

при и |_у =^ — -и₀ из уравнения (19): h ■ с₁ + с₂ — -и₀ находим с₁ — - ^^.

Учитывая, что соотношение (18) получили из условия несжимаемости (14), которое необходимо интегрировать в каждой из областей S ₁ и S ₂. Поэтому скорости перемещений и скорости деформаций будут найдены:

и —

и о

и

( ^- C 1 ^x+f 1 ⁽ yX XES 1 . I -с 1 Х + f^(y), X ES 2 ’

^и ху  ^

f1'(y) 2 f^y)

,X Е S1

, X Е S₂

Интенсивность скоростей деформаций имеет вид:

12., .        12 ,2 , „..2 , ..2 Л ии     3 UijUij     3 ^хх + 2иху + иуу)   <

W⁺ I?"

2(АТ

2(Г)2

^{+ с} 1 )

^{+ с} 1 )

74q² + (f')² ------—-----,Xr, < X < I

V3 p

J 4с ? + (f^ -----=----,—l < X < X_n ■ V3                  ^p

Интегрирование двух уравнений равновесия (5) с учетом, что касательное напряжение ^_х у не зависит от координаты x , дает оценки нормальных напряжений

^ уу

-fW;

^ хх

^{— 2} ^^i

- ^ху(у) + ^уу(Х).

В последнем соотношении перед квадратным корнем сохранен знак «плюс», так как О уу < 0, а 1° уу 1 >  1°_хх1 по физическому смыслу задачи . Далее, интегрируя первое уравнение равновесия системы (5) с учетом (23), имеем

^ ху — f' ⁽ x)■y + с₃. (24)

Из вторых соотношений (15) и (16) заключаем, что в волокне слоя, совпадающим с осью x и на контактной границе с учетом (24):

при у — 0: (x) ■ 0 + с₃ — 0 находим постоянную интегрирования с₃ — 0;

при у — h: f ’ (x)^h + c₃ — -t_s находим функцию f ' (x) — -^.

Полученный результат подставим в уравнение (24):

f ' (x) —

(

—

? s

h

,

Ts +т h

xp < x < l2

l1 < X < Xp

Интегрируя (25), придем к соотношениям

^T s

I — ■ X + c4, f(x) = TS

{~h'x + c4’

Ху < X < ly p          2

ll < X < Xp

° xy (y) =

( ^Ts            . . ,

~И'У’ X p 2

Ts            , .      .

— ■y,   l i p

Из сравнения значений o_x y по формулам (6), (7), (25) видно, что для верхней части полосы при (y > 0) fi’(y) >  0,f[(y) < 0, поэтому интегрируя (25), получаем

К (ri =

^(-^■У 2W

h

2voy

s

^^^^^H

(ri2

■ y2

—

T s 4—

^^^H

y2

hj—

^^^H

y2

После интегрирования

K(y) = - 2 * 4—

^^^^^H

y2 + cj,

Из (23) и (25) имеем

®xx

p =

®xx

—

^ yy

кЫ=^4—

^T s

~r ■X h

—

T s

^^^^^H

y2 + c5.

^^^^^H

T ■x h

^c 4 ^{+ 2} \ ^T ‘ ^H (Ж

y2

^^^H

c 4 +

^T s        I

— ■ X + c, h

F®‘

y2

;

- $H 12(rx + c4

’ 4) H ft:

) + 44

s

s

^^^^^H

a2y2,

^X p

< X < l2

■

^^^^^H

a2y2,

^l l

< X < Xp

Выпишем интегральные условия для определения постоянных c₄,c 4 ,

h

h

c5,cj

V о ^ ^l 2

^^^^^H

Hq i h- Ja_xx\_{X = l}

h

Xp) - J ^u \

о

h

V₀(l i +X p ) - Ju\

о

о

X = l2

x - l_l

dy =

dy =

о

-

dy; 0 =

J ^ xx \

о

T.

s

^^^^^H

—I hll

^^^H

Vo 2 —

^T s

X -l 2

dy ,

-

T.

s

T.

s

h^

-

T.

s

^^^H

— 2 ^y

Условию растяжения на торце полосы отвечает q_l< 0 (\q_l\

^c 4

- h q i h + T s l + 2

о

c4 =

Из условия непрерывности a_yy при х - х_р следует

^X p

h (c4

^^^H

c 4 )

q ± h

2ts

2ts

<

h^ s

2ts

Tsj + c5^

dy,

^^^^^H

^Ts^ ^{+ c} 5 ^

dy^

о^ Из (30) получаем

,

2 ^—

Из (37) следует, что в случае свободно растекающейся полосы с симметричными условиями на концах (q₁ = 0) имеем х_р = 0.

*!         2’о( с = = ьрх р —р.

L-^yiyy\,c*5 = —с5 — 2 ’ " Xр .          (38) h2                     h

Отметим, что, если сближающиеся инструменты (захваты) перемещаются вдоль оси Ох со скоростью u_o(t), то условия (38) для определения с₅,с ^ видоизменяются

^ о (А - * р ) = IO I - U o )dy,                       (39)

^х = ^l 2

о

’ о (1 1 + х р ) = | (и \_{x = l} + U o )dy.                         (40)

о

Задача 2. Рассмотрим приведенное решение в совокупности с пластическим растяжением полосы. Подобный процесс существенно зависит от общей силы сжатия P ₀ захватами краевых участков полосы. При значениях P ₀, превышающих некоторое критическое значение P ^cr жесткий захват полосы не обеспечивается ввиду того, что в зонах сжатия краевых участков полосы, еще до того, как начнется процесс растяжения, металл будет вытекать из-под захватов. При дальнейшем деформировании происходит утонение и разрыв полосы вблизи внутренней границы контакта с захватом. Пусть l₁(t) < |Х| <  l₂(t) — область контакта с захватом, а 0 < 1X1 < l₁(t) — область пластического растяжения (рис. 5).

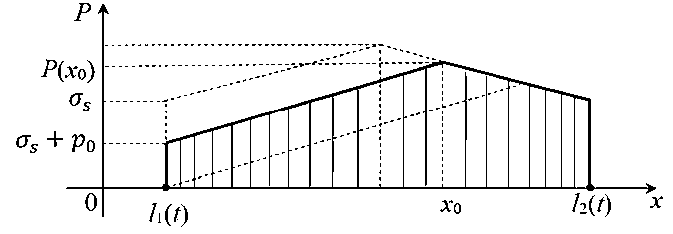
Рис. 5. Распределение контактного давления в области захвата

В области контакта полосы с захватом решение сохраняется, но нужно сделать преобразования

Х(х) = х ^ --2 ,l 2 — l 1 = 21,1 1 ^ Х ^ l₂

и принять условие (39) вместо (33), тогда получим

1[

^{C s} = j Г’ " ¹ ’

’_о [ /      ~?                )

2^J \2 ~№? УУ ^о^Уч-

Выпишем в новых переменных, согласно (41), выражение для о уу :

в уу

=[—^Х(х) \ у[^Х(х)

—

—

^l 1 + ^l 2 2

^l 1 + ^l 2

■1-

с₄; Х_р(х) < Х(х) < l₂

— с₄ * ;    l₁< Х(х) < Х_р(х)

.

Положим, что полоса тонкая: ^|l 2 ^{— l} 1 ^| » h. Найдем величину критической силы Р^сг . Суммарная сила пластического сжатия торцов с учетом (41) будет

Р^сг =—'h i Cl²—х ’ ) — С 4* (х_р + l) — C 4 (l—х_р),                  (44)

где с₄ * ,с₄,х р определены формулами (35), (36) и (37).

Можно показать (см. рис. 5), что P ^cr , полученное согласно (44), меньше соответствующего P ₀, необходимого для «чистого» сжатия той же части полосы со свободными концами. Найдем общую растягивающую силу

* 2

^{F p} = \ Ъу№ = 2r_sV

* 1

Задачу решаем в области |Х| < l1(t) в предположениях, что компоненты скорости зависят только от одной координаты и = и(х), v = v(y) , тогда получим и = —с1х;             v = с1у,

^V XX      ^v yy      ^с 1 >

vxy   О,

^v u

2с1

Г— f 7з

_ dh

^{C 1} hdt’

где h(t)– толщина части полосы, подверженной растяжению. Согласно (31), поле скоростей дефор- маций однородно.

Для силы сжатия приторцовых участков полосы Ро < Рсг имеет место лишь «чистое» растяжение средней части полосы. При Ро > Рсг одновременно с растяжением происходит пластическая осадка участков под захватами. Причем зависимость между скоростью перемещения захватов u0(t) и толщиной h(t) с учетом уточненного условия (42) для с* , £*, можно найти из условия непрерыв-

С 1           ³ ±_*         *

ности u = u ( x, t) в точке X = l₁(t): u_o(t) = — — (l], + l ? ) — f₁ , где f₁ - осредненное по толщине значение функции f * (y) .

Теперь найдем законы изменения l₁(t) и l₂(t)

^1 = и„(1)-, ^—(b — iJ+h+^.iA dt           dt 2                         t = О

= l^, (l = 1,2).       (47)

Точность использованного решения Л. Прандтля – А. Надаи для осадки пластических полос тем выше, чем меньше толщина пластического слоя по сравнению с линейными размерами зоны кон *

такта. Поэтому, пренебрегая в (47) членом f , который мал по сравнению с другими слагаемыми *

^

h т^ 1,

имеем dl1 dt

dh l₁ + l₂ dl₂ hdt 2 ^, dt

dh

^{—     l}2⁽ t).

hdt

Решаем полученную систему (48) методом исключения переменных

=^^(t)= k ⁺ (4—4=W1- ^h(t)                   Vh XhJ Vh

Подобная задача для частного случая решена в работе [18].

Задача 3. Правка полосы растяжением. Пусть края растягиваемой полосы подвержены сжатию захватами вблизи торцов. Найдем предельное значение общей силы сжатия торцов, при достижении которого одновременно с растяжением полосы будет иметь место пластическая осадка сжатых приторцовых зон, расположенных под захватами, и которая мешает осуществлению процесса прав- ки. Сформулируем задачу в рамках теории течения в тонком пластическом слое:

du dA о дх dt ^,

dp      2t_s и — u₀    \ h ’      ^x o ^(t) <  ^х <  ^l ? ^(t)

ta = ^{—                  2} T , ’l_i(_t)o(_t)

h где u = u0(t) – скорость движения захвата в направлении толщины слоя, которая считается заданной;

x = x₀ ( t ) – неизвестная линия ветвления течения; h = h₀ ( t ) – известный закон изменения толщины зажатой захватами части полосы.

Краевые условия задачи:

x = x0(t):u(x, t)	= U 0 (t).		(51)
.2	2 dt du
x = l 2 ( t): схх = -p+-C s	1 3 C sdAdx =	0.	(52)
. 2	2 dt du
x = l i ( t ) : oxx = -p + -C s	1 3 C sdAdx =	C s .	(53)

Условие (52) означает, что граница х = l₂(t) свободна от нагрузок, а (53) подтверждает, что на внутренней границе области контакта x = l_i (t) растягивающее напряжение достигает предельного значения c_s . Решаем (49) с учетом (50):

и(х, t) = —(x < x0(t) ) + u0(t).

Условия (52) и (53) разрешим относительно контактного давления: 4                  1

P2 = P(l2.t) = -с^.Р! = p(li,t) = c°s-

Интегрируем уравнение равновесия (50) с учетом условий (52) и (53):

( 2T s

P2 +~r(lz -x),xo(t)

2T                                   .(55)

Pi + -r(x - li).li(t) 0(t) h

Находим точку ветвления течения x = x₀(t) из условия непрерывности давления в этой точке:

p(x0 + 0. t) = p(x0 -0.t) ^ xQ(t) = 11 + 2 + ~rh.(56)

В случае тонкого слоя

(h«1)

формула (56) упрощается: x₀(t) =

^1 + ^22

Теперь можем найти предельную общую силу сжатия торцов полосы, приходящуюся на единицу ширины захвата, при которой в процессе растяжения пластины из-под захватов, сжимаемых торцов, вытекает часть пластической среды:

^2

X₀

Pcr = j p(x,t)dx = j C ii                             ii

h

Pi+^T-(x- li)^dx + j ^2+-^ (l2 - x)^dx = x0

(px + — —         + (px + — (lx~ —     2-

[Pix+h[2 lix))\x = i+[P2x+ h[l2x 2))\x = x0 =

-     T 2Ts(x₀² , \    , 2Ts(li²    Л        ЪАЬ,² A

= Pixo+~[~-lixo)-Pili-~[-2-li )+P212+~[t-12 )-

-P2x0

—

2t-       x^A _

h \   °    2 ) =

= ^x0^(p1^P2^{) P}i^li^{+ P}2^l2⁺L n (^2x0^{2 2x}o^(li ^{+ l}2^ ^{+ l}i ^{+ l}2 ) =

h 2

= ^x0⁽Pi ^-Pl) ^-Pi^li ⁺P2^l2⁺ "h^{- ((x}0 ^-hY ^{+ (x}0 ^{- l}i⁾²⁾.

Подставим значения p_i>p₂>l_i>l₂ и, учитывая условие для тонкого пластического слоя, получим:

per

= ^js

^l1 + ^l2

+

^4l2 ^-11

4--p= ('2 2h/3 ²

^^^H

S((₂ -11) '^гЦ^-^“

+

('2 - '1)²

2h/3 ,

= Js

('2-Ш573 2V3- \ 6

'2

)■

Очевидно, что P_o > P^cr^

В качестве примера проведем расчет с соответствующими исходными данными:

l₁ = 10 мм, l₂ = 20 мм, h = 2 мм, s = 17 МПа,

(1МПа =

106H м2

= 1 МН/м2):

_ncr     ('2-'i)/5V3 '2-1Л 17 ■ (20 - 10) /5/3 10

^Js 2/3’ \ 6 ⁺h ^j       2/3’    \ 6 ⁺2

170 ■ 7,887

3,464   ~

387,064(H)

При сжатии захватами торцовых частей полосы толщиной h = 2 мм, длиной зоны захвата l₂ - l₁ = 10 и шириной 3 = 10 мм сила, необходимая для перевода деформируемой зоны в пластическое состояние, равна 0,387064 (кН).

ВЫВОД

В рамках модели идеально-пластического тела в представленной работе заработана математическая модель для решения плоской задачи о пластическом растяжении тонкой полосы с одновременным сжатием захватами приторцовых участков в режиме однородного поля скоростей деформаций, при котором полоса выдерживает необходимые пластические деформации при правке растяжением, сохраняя постоянную толщину на всей ее длине – растягиваемого и сжатых участков.