Pre-quarantine Approach for Defense against Propagation of Malicious Objects in Networks
Автор: ChukwuNonso H. Nwokoye, Godwin C. Ozoegwu, Virginia E. Ejiofor
Журнал: International Journal of Computer Network and Information Security(IJCNIS) @ijcnis
Статья в выпуске: 2 vol.9, 2017 года.
Бесплатный доступ
This paper revisits malicious object propagation in networks using epidemic theory in such a manner that it proposes the (Pre-quarantining) of nodes in networks. This is a concept that is known by experience to be a standard disease control procedure that involves screening and quarantining of immigrants to a population. As preliminary investigation we propose the Q-SEIRS model and the more advanced Q-SEIRS-V model for malicious objects' spread in networks. This Pre-quarantine concept addresses and implements the "assume guilty till proven innocent" slogan of the cyber world by providing a mechanism for pre-screening, isolation and treatment for incoming infected nodes. The treated nodes from the pre-quarantine compartment are sent to the recovered compartment while the free nodes join the network population. The paper also derived the reproduction number, equilibria, as well as local stability of the proposed model. Numerical methods are employed to solve the system of equations and MATLAB is used to simulate the system so as to visualize the dynamical behavior of the models. It is seen that pre-screening/pre-quarantining improves the recovery rate in relative terms.
Pre-quarantine, Epidemic model, Wireless sensor network, Malicious objects
Короткий адрес: https://sciup.org/15011749
IDR: 15011749
Текст научной статьи Pre-quarantine Approach for Defense against Propagation of Malicious Objects in Networks
Index Terms —Pre-quarantine, Epidemic model,
Wireless sensor network, Malicious objects.
-
I. Introduction
With the advent of the era of cloud computing and the Internet of Things (IoTs), the threat from malicious codes have become increasingly serious [2]. This is due to the criticality of technological networks as a tool for daily life and the fast development of hardware/software technology viruses [1]. Since the emergence of virus in the 1980s as programs or complex codes, these malicious objects have been renowned to be able to disrupt the correct operation of a machine causing major damages and irreparable financial losses. In recent times viruses perform devastating operations such as modifying data, deleting files, encrypting files, and formatting disks [3] and even more once it breaks out in networks such as Peer-to-Peer (P2P), Wireless Sensor Networks (WSNs).
WSNs are emerging as a rich domain of active research involving hardware and system design, networking, distributed algorithms, programming models, data management, security and social factors [36]. WSNs are large numbers of minimal capacity sensing, computing, and communicating devices which are random deployed without an engineered or predetermined positions for the sensor nodes [5, 6, 7]. The random nature of sensor nodes most times limits operations and activities of WSNs to complex and noisy real-time environments [4]. These sensors can be used for precision farming and environment monitoring. The susceptibility of WSN to attacks [8] from worms or viruses which result in disrupting the measures of confidentiality, integrity and availability of sensor nodes are due to its highly distributed nature. As [7] puts it, cyber attack by worm presents one of the most dangerous threats to the security and integrity of the computer and telecommunications networks.
-
II. Related Works
The spread of malicious agents in the technological networks bore a strong semblance to the spread of epidemic in the biological world [9]. The SIR dynamic model proposed in [10, 11, and 12] for malicious objects propagation initiated the journey of developing mathematical models for worm/virus propagation. Later the works of [13,14] presented an extension of the kermack SIR model by developing the SIS model and [15] proposed an improved SEI model to simulate virus propagation in a peer to peer network. Much later Yan and Liu [16] proposed the SEIR model; therein they assumed that the recovered hosts have a permanent immunization period with a certain probability, which is not consistent with real situation. Newman [17] applied the Kermack and McKendrick classical SIR epidemic model to schemes of email virus spread. Mishra and Jha [18] formulated the SEIRS epidemic transmission model of malicious objects in computer networks. Their assumptions involved a certain death rate other than the attack of malicious object which is constant and an excess death rate constant for infective nodes. Yuan and Chen [19] proposed the new e-SIER network virus epidemic that considers multi-state antivirus, latent periods before the infected hosts become infectious and point to group information propagation mode.
The similarities between epidemics in both the biological and technological networks are evident in these works that employed the epidemic theory (or models) in their analyses. For the study of epidemics in biological networks we have the following. Reference [20] evaluated the impact of variations in periods on contagious dynamics using the SEIRS mathematical model in other to prevent communicable disease spread by setting apart infected hosts. Employing the novel expression by [39] for saturating contact rate, [21] showed the existence of two equilibria in the SEIR model. Taking into account treated and untreated states which form several pathways of infections in SIR and SIER models [22] analyzed attributes for the global dynamics for infectious diseases. By assuming that the entire population of hosts has an invariable density and a bilinear kind of mass action [23] performed analysis on the SEIR model for direct/indirect contact and eggs/seeds transmissions. Li et al. [24] analyzed the global properties for the disease persistent equilibrium in a condition where Exposed and Immune states were infective. In view of the benefits of counseling services in lifestyle habit modification [25] particularly directed analysis to the asymptotic stability (global) of the existent equilibria in the proposed SEIR model using the Holling Type II incidence function for the counseled and the uneducated infective states.
Lending credibility to the definition of the word “quarantine” which means the forced isolation or stoppage of interaction with others, [28] posits that one way to control the spread of worms for the nodes which are highly infected is to be kept in isolation for some time. Furthermore transmission of infection to susceptible nodes may be minimized. However, several authors have applied the quarantine strategies to disease propagation models. In a SIQR model for childhood disease, Wu and Feng [26] showed that some perturbation of the original model might have a homoclinic bifurcation in addition to an epidemic approximation observed near R0 = 1. Feng [27] examined the impact of isolation i.e. quarantining infected hosts in the recurrent outbreaks of childhood diseases. SEIQR models with arbitrary distributed periods of infection including quarantine were posited by [28, 29]. With emphasis on infectious diseases [30] studied the effect of quarantine in six endemic models with different form of incidence.
On the application of quarantine using worm/virus propagation models; Zou [31] proposed the dynamic quarantining of hosts and performed analysis on three worm spread models by halting the movement of signals and messages through the suspicious port so as to show an increased epidemic threshold. Toutonji [32] established worm propagation models on the basis of constant quarantine strategy (using a benevolent passive worm); though the stability analyses of their systems were not taken into account in their works. To abate the spread of internet worms [33] conceived a combination of dynamic quarantine and vaccination strategy to obtain the reproductive ratio and to study the significance of several parameters. The effect of isolating a virus-infected file and the use of anti-malicious software was considered by [35]. They proposed an SEIRQ model for the transmission of virtual threats in a network. Pursing a different perspective to isolation of infected/infective hosts [34] proposed the pulse quarantine strategy (adjudged as better than the constant quarantine strategy). In a conscious bid to ensure security in sensor networks [6] extended the classic model to include the Vaccinated compartment by formulating the SEIRQV mathematical model. The SEI model in [15] was improved by Haldar et al. [48] so as to study the effect of trust, selfishness and collaborative behavior during a wireless network epidemic.
The “ Pre-Quarantine ” concept proposed in this study is non-existent in the available literature in the sense that most researchers [7, 40-47] in this area do not check the status of immigrant nodes. They assume that nodes entering a network are susceptible to attack; this is partly true. The implication is that to a large extent the nodes entering the network are free from the modeled infection/threat type; and this is not always true in the real world. Or more appropriately, the disease status of the incoming nodes is not known. Specifically, we explore the concept of pre-quarantining of incoming sensor nodes to provide a screening mechanism that would isolate and treat infected nodes from the population that enters the susceptible compartment. However, the study considers the disease status of the nodes entering the network population. To ensure a worm/virus-free cyberspace it is overly expedient that research efforts are directed to provide countermeasures for malicious objects/cyber threats propagation in networks from all avenues possible. It is our hope that the proposed models would add to the extant epidemiological literature of networks.
-
III. Pre-Quarantining Q-Seirs Model Without Vaccination
To describe the dynamics of the pre-quarantine concept for virus propagation with respect to time in a wireless sensor network we propose the Quarantine-Susceptible – Exposed – Infectious – Recovered – Susceptible model. Our assumptions include the addition/inclusion of new nodes and the death/crashing of nodes either due to hardware/software failure or due to infection. Initially we assume that the new nodes go through a screening process and treatment (prequarantine) in the Quarantine compartment. However, the infected nodes in the pre-screening process are treated with anti-malicious software and sent to the Recovered compartment while the nodes that have been proven free of infection enter the network field i.e. becoming susceptible (in the Susceptible compartment) again to infections. The Exposed compartment here signifies the latent phase before the nodes get fully infectious. Infectious nodes carry the infection and can transmit it to neighboring nodes. Infectious nodes are sent to the Recovered compartment where they are temporarily immune by treatment with an anti-malicious software. They subsequently enter the susceptible compartment and are vulnerable to possible attack of malicious objects because there is no permanent immunity in the cyberspace.
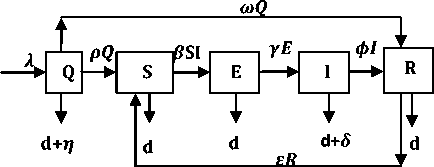
Fig.1. Schematic Diagram for the Flow of Malicious Object in a Wireless Sensor Network
The population size N (t) is compartmentalized into subclasses of nodes which are Q (t), S (t), E (t), I (t), R (t) respectively. Our assumptions on the dynamical transfer of the population are depicted in the Fig 1. It is seen from the loop that the dynamics of the pre-quarantining (prescreening) compartment is governed by the first order differential equation:
Q = л - Q(d + ^+ p + w ) (1)
Where Qo is the initial population, the solution of this equation is derived from the convolution integral as:
Q ( t ) = e -(d+ n + P +Ш ) tQ + ^ [1 — e -(d+ n + p +ш ) t ] 0 (d + n + P + to )
The system of differential equation in view of our assumptions is:
S = p Q + sR- S(PI + d) Ё = PSI - E(y + d)
I = yE —1( ф + d + S) (3)
R = toQ + >I-R(E + d)
Let Q (t), S (t), E (t), I (t), R (t) denote the number of Quarantine, Susceptible, Exposed, Infectious and Recovered nodes at time t respectively. Assume N (t) = Q (t) + S (t) + E (t) + I (t) + R (t) for all t, where S = ^ Л is the inclusion rate of nodes into the network population, P is the Infectivity contact rate, d is the mortality or the death rate of nodes due to hardware or software failure, r) = death rate of infected immigrant nodes, S = is the crashing rate due to attack of malicious objects, ф = rate of transmission from Infectious to Recovered class, is the rate of transmission from Recovered to Susceptible class, is the rate of transmission from Quarantined to Susceptible class, is the rate of transmission from Exposed to Infectious class, to = rate of transmission from Quarantine class to Recovered class.
-
A. Existence of Equilibrium Points
The equilibrium points of (3) are the solution of the system of ordinary differential equation. Therefore, we have;
dS dE di dR
— = 0; = 0; -г = 0; = 0.
at at at
The solution of the system of differential equation is a closed set i.e. it enters or remains in the epidemiological meaningful subset;
D = {(S, E, I, R) E ; S + E +1 + R < N}.
The solution is considered in region D. Since the solution remain bounded in the positively invariant region D, the maximal interval is (0, m) [38] hence posing the initial value problem both epidemiologically and mathematically.
The system of equations has two possible equilibria in D; the disease free equilibrium (DFE) and the endemic equilibrium (EE). On simple calculations the disease free equilibrium ( ET ) has the following states:
S 0 ^ ^"(l^r^ ’E 0 = 0,I O = 0,R 0 = ^ ;
While the endemic equilibrium ( EN ) has the following states:
„* _ (d +Y)(d+S+0)
Yy’
(Q * ш£ _(_ d - E )(Q . p _dW±/)W±^) ))(_ d _ 5_ ф )
g * _ _______________V___________ Pr ______'___________
— (d +Y)(d+S)(d+£)+d(d +y+e) Ф’
, _ (Q * Ш£- (-d- =)(Q * p- d(^r)^*) ))^d_5_ф)
-
1 = (d+T+w^JT^st^,
* . _ Q'e ( » ( d + Y )( d + - ? ) + to ( d + Y ) Ф + /РФ ) — d ( d + Y )( d + ^ ) Ф — d ( d + Y ) ф2 = в ( d + Y )( d + < ? )( d + E ) + de ( d + Y + E ) ф
Where Qi is the value of Q at equilibrium such that Q * =------
(d+ T) + p +1)
-
B. The Basic Reproduction Number (Ro)
The basic reproduction number is the spectral radius of FV-1 where the F is the transition matrix (or the rate of appearance of new infections in the Infectious compartment) and V is the Infection matrix (rate of transfer of nodes into and out of the Infectious compartment). V and F are given as;
(y + d) 0 lF=r0 P
-y (> + d + 5)J’ F *0 0+
V =[
The basic reproduction number is defined as the dominant eigenvalue of FV -1, which is R 0 =
-
C. Local Asymptotic Stability of Disease Free Equilibrium, ET
Here, we employ the Jacobian stability approach [37] to prove the stability of the disease free equilibrium state.
Theorem 1 : The system of ordinary differential equation i.e. (3) is locally asymptotically stable at the disease free equilibrium if its eigenvalues have negative real parts.
Proof : The Jacobian of system (3) is taken as
|
( )= |
|
∗( ) - 0 |
|
( ) |
|
⎢⎢ 0 -( + ) ∗ ( ) 0 ⎥⎥ (4) |
|
⎢⎢ 0 -( + + ) 0 ⎥⎥ |
|
⎣ 0 0 -( + )⎦ |
The diagonals of the Jacobian matrix are– ,-( +
),-( + + ),-( + ) while the eigenvalues are:
{ - d , - d - e ,
- 4d (2 d + y + 6 + ф ) - 4d d2 Q• Pyp + 4 Q" Pye 2( p + m ) + d ( y 2 + ( 6 + ф )2 - 2 y ( 6 + ф - 2 Q" Pe (2 p + m )))
2 d
- 4d ( 2 d + y +
6 + ф ) + ^ 4 d 2 Q" Pyp + 4 Q" Pye 2 ( p + m ) + d ( y 2 + ( 6 + ф ) 2 - 2 y ( 6 + ф - 2 Q" pE ( 2 p + m
2 d
1}
The eigenvalues of the Jacobian matrix all have negative real parts when
| ^4 d2Q* Pyp + 4 Q "Pye 2 ( p + m ) + d ( y 2 + ( 6 + ф ) 2 - 2 y ( 5 + ф - 2 Q*pS(2 p + m ) ) ) | < dd ( 2 d + y + 6 + ф ) ;
hence the system is locally asymptotically stable at the Disease Free equilibrium point .
-
IV. Pre-Quarantining Q-Seirs-V Model With Vaccination
To describe the dynamics of the pre-quarantine concept for malicious object propagation with respect to time in WSN we propose the Quarantine -Susceptible – Exposed – Infectious – Recovered – Susceptible with the Vaccination class. The case without the vaccination class is studied in subsection 2 in a bid to form a foundation for the study in this subsection. Initially we assume that the new nodes go through a screening process (prequarantine) that allows the infected nodes to be treated and sent to the Recovered compartment. The nodes that have been proven free of infection enter the sensor field i.e. becoming susceptible (in the Susceptible compartment) again to malicious object infections. The other assumptions for this subsection are the same as the assumptions in section 2. Vaccination of the susceptible nodes provides further an immunization capability toward infections as well as enabling procedures for the control of malicious objects. The proposed model is expected to provide more insight into the understanding of the epidemiological behavior of a population of nodes.
Note that quarantine and vaccination are the most commonly known countermeasures for disease propagation in the epidemiological literature.
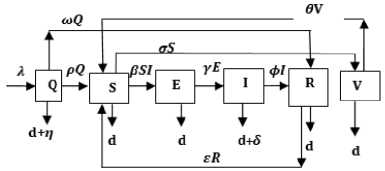
Fig.2. Schematic Diagram for the Flow of Malicious Object in a Sensor Network
It is seen that the dynamics of the proposed prequarantining compartment is the same as the earlier studied case without vaccination. The system of differential equation in view of our assumptions is given as:
̇= + + - ( + +)
̇= - ( +)
̇= - ( + + )(5)
̇= + - ( +)
̇= - ( +)
= rate of transmission from Infectious to the Recovered class. = rate of transmission from
Vaccinating class to Susceptible class, is the vaccinating rate coefficient for the susceptible nodes. The other rate symbols retain the same meaning as in section III.
-
A. Existence of Equilibrium Points
The equilibrium points of (5) are the solution of the system of ordinary differential equation when the rate of change vanishes;
=0; =0; =0; =0; =0 .
clt clt clt clt clt
Two possible equilibria exist in D; the Disease Free equilibrium and the endemic equilibrium. On simple calculations the Disease Free equilibrium ( ET ) has the following states:
∗( )( ())
( )( )
= 0,= 0,
∗ ∗ ()
, ( )()
However, if > 1 then D contains a unique positive endemic equilibrium ( EN ) that has the following states:
( )( ) ∗ (Φ ∗( ) ∗ )()
∗ (( ∗ Ω) ∗ )( ))()
= ( )(Ψ )
R*
.fy ( - d - 6 - Ф M( - d - e )( Q* p - d П) - Q ‘ero )
______________ ( d + 6 + ф )(T - Еф) _________ d + e
V* =
о (у
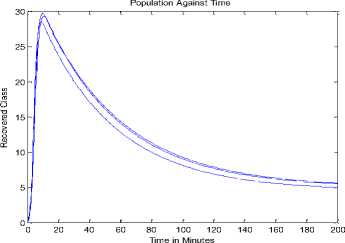
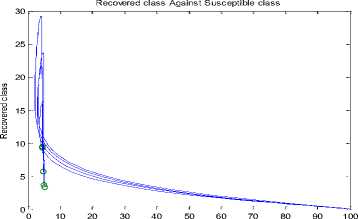
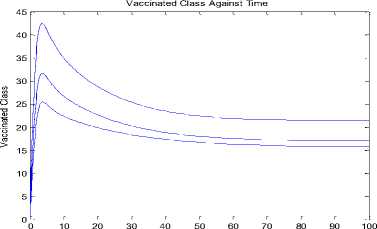
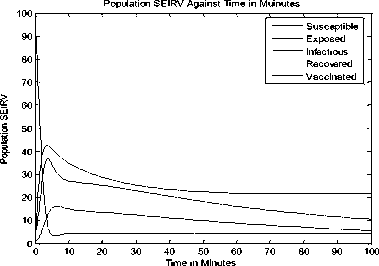
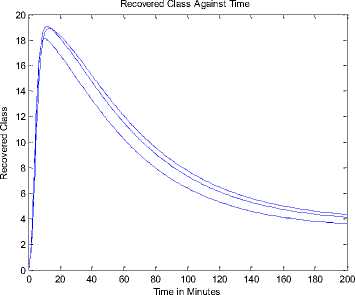
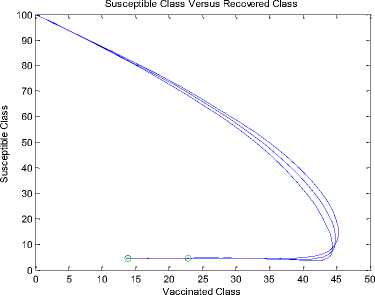
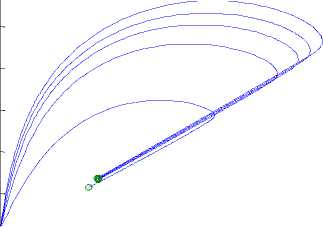
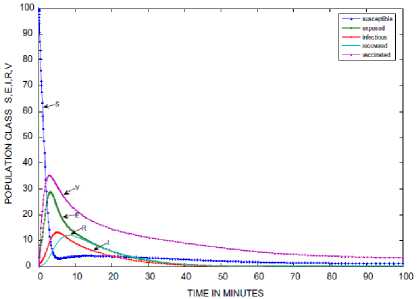
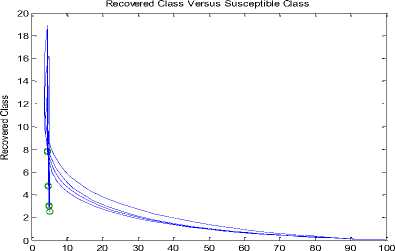
+ d)( Where Ф = d (d+ y)(d+s((d+9+ ) PW^ , (d + y)(d+9 +o")(d +5+ +УУ)(d+E)(d+5+ PY (d+9) , У B. The Basic Reproduction Number (Ro) The basic reproduction number can be obtained by calculating V and F, where V and F are given as; (У + ^ 0 1рГ0/?1 —y ( V =[ Where V is the rate of transfer of nodes into and out of the Infectious compartment and F is the rate of appearance of new infections in the Infectious compartment. The basic reproduction number is defined as the dominant eigenvalue of FV -1, which is R0 = (y+ d) (++d +5) C. Stability of the Disease Free Equilibrium To obtain the stability of the equilibrium state the resulting eigenvalues of the jacobian of the system are derived as follows: -( d + a ) 0 - PQ *( d + 9)( dp + s (p + ®)) d (d + s)(d + 9 + a) s 9 J(ET) 0 -(/ + d) PQ *( d + 9)(dp + s (p + ®)) d (d + s)(d + 9 + a) 0 0 0 Y -(ф + d + 5) 0 0 0 0 ф -(s + d) 0 . a 0 0 0 -(9 + d) The diagonal elements are - (d + o), - (y + d), —(ф + d + 5), — (£ + d), —(9 + d) while the eigenvalues are {— d, —d — £, —d — 9 — o, , ^ (d + 9 + a)(-/+5 + ф)2d [ d + s ]+4/(dp + s[ p + ^])PQ*[ d + 9]. - (-2d - у - 5 - ф - --------------------. - ), 2 4d + 9+a4d [ d + s ] 1 ^ (d + 9+a)(-/+5+ф )2d [ d + s ]+4/(dp + s[ p + ®])₽Q‘[ d + 9] - (-2d - у - 5 - ф+ ---------------------. . )}. 2 4 d + 9+a 4 d [ d + s ] The eigenvalues of the Jacobian matrix all have negative real partswhen , vTdd+F+Ty^T+n^ipfddidd+n+ydfH+H^^ ।, 1 Vd+e+CTydid+^ 1 < 2d + y + 5 + ф; hence the system is locally asymptotically stable at the Disease Free equilibrium point ET. V. Results and Discussion In most models [6-7, 35, 40, 43-44] in the available literature it is observably clear that the recovered compartment evaluate to zero at the disease free equilibrium unlike the models of this study. Here the recovered compartment is not equal to zero i.e. R * 0; and this is as a result of the transfer of some immigrant infected nodes which were successfully treated (during the pre-quarantine process) and transfered to the Recovered compartment as well as the re-infection (due to temporary immunity) of nodes and death from software and hardware failure. The resulting solution of the recovered compartment at disease free equilibrium is R° = Q* Another feature is the fact that the reproduction number (R0) is similar in these models. In addition, since the Vaccination compartment has transmissions to and from the Susceptible compartment and the value of 5* is used to determine the value for V* at endemic equilibrium; it gives that the Q-SEIRV model and [6] would have similar values for V*. For the same values in reproduction number, the implication is that prequarantining of nodes does not affect the reproduction number of models derived using similar equations of Exposed and Infectious compartment in [6-7]; otherwise the R0 changes as noted in [43]. Aside the noted similarities in this paragraph, the current study presents radically different values in both equilibrium states when compared to [6, 7, and 35] etc. The basic difference in assumptions between the current study and the work [7] is that it is presumed here that immigrant nodes that enter the network could be infected while the work [7] implicitly presumed that immigrant nodes to the network are free of infections. However, it is rational to suppose that the assumptions of the current study are more realistic in real world applications. The proposed pre-quarantining concept intercepts immigrant infections and checks the potential for enhancement of the internal infectivity contact rate through importation of external infections. The intercepted infected immigrant nodes are treated in the pre-screening process leading to some assuming temporary immunity in the recovered compartment. For these reasons the rate of recovery is expected to be enhanced in the proposed model as evident in Fig 3. and Fig 7.; in which the Recovered compartment is seen to have higher peak values than the Infectious compartment unlike the result in the equivalent model in [7] without prescreening given in Fig.13; in which the peak value of the Recovered compartment is less than that of the Infectious compartment. A. Numerical Results for the Q-SEIR We present the numerical results using Runge-Kutta Fehlberg method of order 4 and 5 for the Q-SEIR model. The network is assumed to have initial values: Qo= 5; S=100; E=3; I=1; R=0. Fig.3. Dynamical Behaviour of the System for Different Classes When λ=0.33; ρ=0.3; ω=0.01; η=0.001; ε=0.3; β=0.1; γ=0.25; φ=0.4; d=0.003; δ=0.07. Fig.4. Dynamical Behaviour of the Recovered Class With Respect To Time: (1) λ=0.33; ρ=0.3; ω=0.01; η=0.001; ε=0.3; β=0.1; γ=0.25; φ=0.4; d=0.003; δ=0.07; (2) λ=0.33; ρ=0.3; ω=0.03; η=0.001; ε=0.33; β=0.1; γ=0.28; φ=0.43; d=0.003; δ=0.07. (3) λ=0.33; ρ=0.3; ω=0.05; η=0.001; ε=0.39; β=0.1; γ=0.31; φ=0.46; d=0.003; δ=0.07 -5 -5 Recovered class Against Infectious class Infectious Class Fig.5. Dynamical Behaviour of the Recovered Class Versus Infectious class: (1) λ=0.33; ρ=0.3; ω=0.01; η=0.001; ε=0.3; β=0.1; γ=0.25; φ=0.4; d=0.003; δ=0.07. (2) λ=0.33; ρ=0.3; ω=0.01; η=0.001; ε=0.33; β=0.3; γ=0.27; φ=0.42; d=0.003; δ=0.07. (3) λ=0.33; ρ=0.3; ω=0.01; η=0.001; ε=0.35; β=0.5; γ=0.29; φ=0.44; d=0.003; δ=0.07. (4) λ=0.33; ρ=0.3; ω=0.01; η=0.001; ε=0.37; β=0.7; γ=0.31; φ=0.46; d=0.003; δ=0.07. (5) λ=0.33; ρ=0.3; ω=0.01; η=0.001; ε=0.39; β=0.9; γ=0.34; φ=0.48; d=0.003; δ=0.07. Susceptible class Fig.6. Dynamical Behaviour of the Recovered Class Versus Susceptible class: (1) λ=0.33; ρ=0.3; ω=0.01; η=0.001; ε=0.3; β=0.1; γ=0.25; φ=0.4; d=0.003; δ=0.07. (2) λ=0.33; ρ=0.5; ω=0.01; η=0.001; ε=0.5; β=0.1; γ=0.27; φ=0.42; d=0.003; δ=0.07. (3) λ=0.33; ρ=0.7; ω=0.01; η=0.001; ε=0.8; β=0.1; γ=0.30; φ=0.45; d=0.003; δ=0.07. (4) λ=0.33; ρ=0.9; ω=0.01; η=0.001; ε=0.8; β=0.1; γ=0.70; φ=0.47; d=0.003; δ=0.07 B. Numerical Results for the Q-SEIRV We present the numerical results using Runge-Kutta Fehlberg method of order 4 and 5 for the Q-SEIRV model. The network is assumed to have initial values: Qo= 5; S=100; E=3; I=1; R=0; V=0. Time in Minutes Fig.8. Dynamical Behaviour of the Vaccinated Class with Respect to Time: (1) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε =0.3; β =0.1; γ =0.25; φ =0.4; d=0.003; δ =0.07; σ =0.3 (2) λ =0.33; ρ =0.3; ω =0.01; η=0.001; θ=0.05; ε =0.3; β=0.1; γ =0.25; φ =0.4; d=0.003; δ =0.07; σ =0.2 (3) λ=0.33; ρ =0.3; ω =0.01; η=0.001; θ=0.04; ε =0.3; β=0.1; γ =0.25; φ =0.4; d=0.003; δ =0.07; σ =0.15 Fig.7. Dynamical Behaviour of the System for Different Classes When λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.3; β=0.1; γ=0.25; φ=0.4; d=0.003; δ=0.07; σ=0.3 Fig.9. Dynamical Behaviour of the Recovered Class with Respect to Time: (1) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.3; β=0.1; γ=0.25; φ=0.4; d=0.003; δ=0.07; σ=0.3. (2) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.33; β=0.1; γ=0.28; φ=0.43; d=0.003; δ=0.07; σ=0.3. (3) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.39; β=0.1; γ=0.31; φ=0.46; d=0.003; δ=0.07; σ=0.3. Fig.12. Dynamical Behaviour of the Susceptible Class Versus Vaccinated class when (1) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.3; β=0.1; γ=0.25; φ=0.4; d=0.003; δ=0.07; σ=0.32. (2) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.09; ε=0.3; β=0.1; γ=0.25; φ=0.4; d=0.003; δ=0.07; σ=0.35. (3) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.12; ε=0.3; β=0.1; γ=0.25; φ=0.4; d=0.003; δ=0.07; σ=0.38. Recovered Class Against Infectious Class 5 10 15 20 25 30 Infectious Class Fig.10. Dynamical Behaviour of the Recovered Class Versus Infectious class: (1) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.3; β=0.1; γ=0.25; φ=0.4; d=0.003; δ=0.07; σ=0.3. (2) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.33; β=0.1; γ=0.27; φ=0.42; d=0.003; δ=0.07; σ=0.3. (3) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.35; β=0.1; γ=0.29; φ=0.44; d=0.003; δ=0.07; σ=0.3. (4) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.37; β=0.1; γ=0.31; φ=0.46; d=0.003; δ=0.07; σ=0.3. (5) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.39; β=0.1; γ=0.34; φ=0.48; d=0.003; δ=0.07; σ=0.3. Fig.13. Dynamical Behaviour of the System for Different Classes of the Equivalent Model as Adapted From [7] Susceptible Class Fig.11. Dynamical Behaviour of the Recovered Class Versus Susceptible class: (1) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.3; β=0.1; γ=0.25; φ=0.4; d=0.003; δ=0.07; σ=0.3. (2) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.5; β=0.1; γ=0.27; φ=0.42; d=0.003; δ=0.07; σ=0.3. (3) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.8; β=0.1; γ=0.30; φ=0.45; d=0.003; δ=0.07; σ=0.3. (4) λ=0.33; ρ=0.3; ω=0.01; η=0.001; θ=0.06; ε=0.8; β=0.1; γ=0.70; φ=0.47; d=0.003; δ=0.07; σ=0.3. VI. Conclusion Motivated by the epidemic theory, we propose the Q-SEIR and Q-SEIRV models to represent the dynamics of the pre-quarantining of nodes in wireless sensor networks. We establish that the Disease Free equilibrium is locally asymptotically stable. Runge-Kutta-Fehlberg method of order 4 and 5 is used to solve and simulate the proposed systems of equation. With the help of MATLAB, an extensive simulation is performed to validate the developed models. Fig. 3 represents the dynamical behaviour of the system for different classes in the Q-SEIR model under different parametric values and Fig. 4 represents the dynamical behaviour of the recovered class with respect to time. Fig. 5 shows the dynamical behaviour of the Recovered class versus Infectious class. It is evident that the recovery rate is very high in the Q-SIER model. Fig. 6 shows the dynamical behaviour of the Recovered class versus Susceptible class. Fig. 7 represents the dynamical behaviour of the different classes in the Q-SEIRV model and Fig. 8 represents the dynamical behaviour of the Vaccinated class with respect to time. Fig. 9 shows the dynamical behaviour of the Recovered class with respect to time and Fig. 10 represents the dynamical behaviour of the Recovered class versus the Infectious class. The transfer of the recovered nodes to the Susceptible class is depicted in Fig. 11 while Fig. 12 represents the dynamical behaviour of the Susceptible class versus Vaccinated class, showing the strong impact of Vaccination on the nodes when compared to [7]. The impact of the Pre-quarantine compartment in the proposed models is very strong on the recovery nodes as shown in Fig. 5 (for Q-SEIR) and Fig. 10 (for Q-SEIRV). When compared to the model proposed by [7] it is seen that the recovery rate of the models of this study is higher relative to the infectious compartment. It is our hope that this study would add to virtual epidemiology and help software organizations in developing highly efficient plan for anti-malicious software to minimize the attack in wireless sensor networks. In future works, analysis would include the proof of local asymptotic stability for the endemic equilibrium and the proof of global asymptotic stability for both the disease free and endemic equilibrium.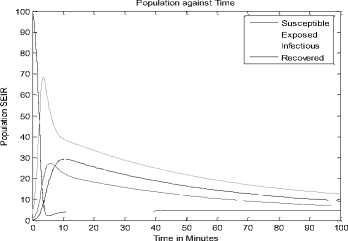

Список литературы Pre-quarantine Approach for Defense against Propagation of Malicious Objects in Networks
- P. J. Denning, Computers under attack, Addison-Wesley, Reading, Mass, 1990.
- K. Hwang, G. C. Fox, and J. J. Dongarra, Distributed and Cloud Computing: From Parallel Processing to the Internet of Things, Morgan Kaufmann, 2013.
- P. Szor, The Art of Computer Virus Research and Defense, Pearson Education, 2005.
- J. Stankovic, "When sensor and actuator networks cover the world," ETRI Journal, vol. 30, pp. 627–633, October 2008.
- E. Lule and T. Bulega,"A scalable wireless sensor network (WSN) based architecture for fire disaster monitoring in the developing world", IJCNIS, vol.7, pp.40-49, January 2015. DOI: 10.5815/ijcnis.2015.02.05.
- B. K. Mishra and I. Tyagi, "Defending against malicious threats in wireless sensor network: A mathematical model," I. J. Information Technology and Computer Science, vol 03, pp. 12-19, February 2014. DOI: 10.5815/ijitcs.2014.03.02.
- B. K. Mishra and N. Keshri, "Mathematical model on the transmission of worms in wireless sensor network," Applied Mathematical Modelling, vol. 37, 2013, pp. 4103–4111, September 2013. http://dx.doi.org/10.1016/j.apm.2012.09.025
- V. C. Giruka, M. Singhal and J. S. Royalty, "Varanasi, Security in wireless sensor networks," Wireless Communications Mob. Comput., vol. 8, pp. 1–24, September 2008. DOI: 10.1002/wcm.422
- B. K. Mishra and G. M. Ansari, "Differential Epidemic Model of Virus and Worms in Computer Network, International Journal of Network Security, vol.14, pp. 149-155, May 2012.
- W. O. Kermack and A. G. McKendrick, A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society A, vol. 115, pp. 700–721, August 1927.
- W. O. Kermack and A. G. McKendrick, Contributions of mathematical theory to epidemics, III–Further studies of the problem of endemicity. Proceedings of the Royal Society of London, Series A, vol. 138. pp. 55-83, 1932.
- W. O. Kermack and A. G. McKendrick, "Contributions of mathematical theory to epidemics, II–The problem of endemicity," Proceedings of the Royal Society of London, Series A, vol. 141, pp. 94-122. 1933.
- N. T. Bailey, The Mathematical Theory of Epidemics, London, Griffin, 1957.
- R. M. Anderson and R. M. May, Infectious Diseases of Human: Dynamics and Control. Oxford, Oxford Univ. Press, 1991.
- W. T. Richard and J.C. Mark. "Modelling virus propagation in peer-to-peer networks," 5th International Conference on Information, Communications and Signal Processing, pp. 981-985, December 2005. DOI: 10.1109/ICICS.2005.1689197
- P. Yan and S. Liu, "SEIR epidemic model with delay" Journal of Australian Mathematical Society, Series B – Applied Mathematics, vol. 48, pp. 119-134, July 2006. DOI: 10.1017/S144618110000345X
- M. E. Newman, S. Forest and J. Balthrop, "Email networks and the spread of computer virus," Physical Review E, vol. 66, pp. 3, July 2002. DOI: 10.1103/PhysRevE.66.035101
- B. K. Mishra and N. Jha, "Fixed period of temporary immunity after run of anti-malicious software on computer nodes," Applied Mathematics and Computation, vol. 190, pp. 1207-1212, July 2007. DOI: 10.1016/j.amc.2007.02.004
- H. Yuan and G. Chen, "Network virus epidemic model with point-to-group information propagation" Applied Mathematics and Computation, vol. 206, pp. 357–367, December 2008. DOI: 10.1016/j.amc.2008.09.025
- M. A. Safi, M. Imram and A. B. Gumel, "Threshold dynamics of a non-autonomous SEIRS model with quarantine and isolation," Theory in Biosciences, vol. 131, pp. 19-30, January 2012. DOI: 10.1007/s12064-011-0148-6
- J. Zhang and Z. Ma., "Global dynamics of an SEIR epidemic model with saturating contact rate," Mathematical Biosciences, vol. 185, pp. 15-32, September 2003. DOI: 10.1016/S0025-5564(03)00087-7
- Korobeinikov A., "Global properties of SIR and SEIR epidemic model with multiple parallel infectious stages," Bulletin of Mathematical Biology, vol. 71, pp. 75-83, January 2009. DOI: 10.1007/s11538-008-9352-z
- M. Y. Li, H. L. Smith and L Wang, "Global dynamics of an SEIR epidemic model with vertical transmission," SIAM Journal on Applied Mathematics, vol. 62, pp. 58-69, July 2006. DOI: 10.1137/S0036139999359860
- G. Li and Z. Jin, Global stability of a SEIR epidemic model with infectious force in latent, infected and immune period. Chaos, Solitons and Fractals, vol. 25, pp. 1177-1184, September 2005. DOI: 10.1016/j.chaos.2004.11.062
- M. A. Safi and S. M. Garba, "Global stability analysis of SEIR model with Holling Type II incidence function," J Math. Biol., vol. 2012, September 2012. DOI: 10.1155/2012/826052
- L. I. Wu and Z. Feng, "Homoclinic bifurcation in an SIQR model for childhood disease," J. Diff. Eqn., vol. 168, pp. 150-167, November 2000. DOI: 10.1006/jdeq.2000.3882
- Z. Feng and H. R. Thieme, "Recurrent outbreaks of childhood disease revisited: the impact of isolation," Math. Biosci., vol. 128, pp. 93-130, August 1995. DOI: 10.1016/0025-5564(94)00069-C
- Z. Feng and H.R. Thieme, Endemic models with arbitrarily distributed periods of infection, I: General theory," SIAM J. Appl. Mathematics, vol. 61, pp. 803-833, July 2006. DOI:10.1137/S0036139998347834
- Z. Feng and H. R. Thieme, "Endemic models with arbitrarily distributed periods of infection, II: Fast disease dynamics and permanent recovery," SIAM J. Applied Mathematics, vol. 61, pp. 983–1012, July 2006. DOI:10.1137/S0036139998347846
- H. Hethcote, M. Zhein and L. Shengbing, "Effects of quarantine in six endemic models for infectious diseases," Math. Biosci., vol. 180, pp. 141–160, December 2002. DOI: 10.1016/S0025-5564(02)00111-6
- C. C. Zou, W. B. Gong and D. Towsley, "Worm propagation modeling and analysis under dynamic quarantine defense," Proceedings of the 2003 ACM Workshop on Rapid Malcode (WORM 2003), pp. 51–60, October 2003. DOI: 10.1145/948187.948197
- O. Toutonji, S. M. Yoo, "Passive benign worm propagation modeling with dynamic quarantine defense," KSII Trans Internet Inf Syst; vol. 3, pp. 96–107, February 2009. DOI: 10.3837/tiis.2009.01.005
- F. W. Wang, Y. K. Zhang, C. G. Wang, J. F. Ma, S. J. Moon, "Stability analysis of a SEIQV epidemic model for rapid spreading worms," Computer & Security, vol. 29, pp. 410–418, 2010.
- Y. Yao, L. Guo, H. Guo, G. Yua, F-x. Gao and X-j. Tong, "Pulse quarantine strategy of internet worm propagation: modeling and analysis," Computers and Electrical Engineering, vol. 38, pp. 1047–1061, September 2012. DOI:10.1016/j.compeleceng.2011.07.009
- B. K. Mishra and N. Jha, "SEIQRS model for the transmission of malicious objects in computer network," Applied Mathematical Modelling, vol. 34, pp. 710–715, March 2010. DOI: 10.1016/j.apm.2009.06.011
- A. S. K. Pathan, H. Lee and C. S. Hong, "Security in wireless sensor networks: issues and challenges," The 8th International conference of Advanced Communication Technology (ICACT) 2006, February 2006. DOI: 10.1109/ICACT.2006.206151
- P. Driessche, J. Watmough. "Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission," Mathematical Biosciences, vol. 180, pp. 29-48, December 2002.
- J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical Systems and Bifurcation of Vector Fields, vol. 42. Springer Science & Business Media, New York, 2013.
- J. A. P. Heesterbeck and J. A. J. Metz, "The saturating contact rate in marriage and epidemic models," Journal of Math Bio, vol. 31, May 1993. DOI:10.1007/BF00173891
- M. Kumar, B. K. Mishra and N. Anwar, "E-epidemic model on highly infectious nodes in the computer network," International Journal of Computer Science & Engineering Technology, vol. 4, pp. 2229–3345, September 2013.
- B. K. Mishra and G. M. Ansari, "Differential epidemic model of virus and worms in computer network," International Journal of Network Security, vol. 14, pp. 149-155, January 2012.
- B. K. Mishra and S. K. Pandey, "Dynamic model of worm propagation in computer network, Appl. Math. Modell., vol. 38, pp. 2173-2179, April 2014. DOI: 10.1016/j.apm.2013.10.046
- B. K. Mishra, S. K. Pandey, "Dynamic model Of Worms with Vertical Transmission in Computer Network," Applied Mathematics and Computation, vol. 217, pp. 8438–8446. March 2011. DOI:10.1016/j.amc.2011.03.041.
- B. K. Mishra and A. K. Singh, "SIjRS E-epidemic model with multiple groups of infection in computer network," International Journal of Nonlinear Science, vol. 13, pp. 357-362, February 2012.
- B. K. Mishra and N. Jha, "Fixed period of temporary immunity after run of anti-malicious software on computer nodes, Applied Mathematics and Computation, vol. 190, pp. 1207–1212, July 2007. DOI:10.1016/j.amc.2007.02.004
- B. K. Mishra and A. Prajapati, "Spread of malicious objects in computer network: A fuzzy approach," Appl. Appl. Math., vol. 8, pp. 684 – 700, December 2013.
- K. Haldar, B. K. Mishra, "A mathematical model for a distributed attack on targeted resources in a computer network," Commun Nonlinear Sci Numer Simulat, vol. 19, pp. 3149-3160, September 2014. DOI: 10.1016/j.cnsns.2014.01.028.
- K. Haldar, N. Narayan and B. K. Mishra, "A mathematical model on selfishness and malicious behavior isn trust based cooperative wireless networks", IJCNIS, vol. 7, pp.15-22, September 2015. DOI: 10.5815/ijcnis.2015.10.02


