Рассматривается космический аппарат (КА) землеобзора, оснащенный телескопом с матрицами оптико-электронных преобразователей (ОЭП) в его фокальной плоскости. При съемке заданных участков поверхности Земли совокупностью маршрутов их сканирования телескопом матрицы ОЭП «работают» в режиме временной задержки и накопления (ВЗН). К системе управления ориентацией (СУО) маневрирующего спутника землеобзора предъявляются уникальные требования по точности стабилизации его движения при сканирующей оптико-электронной съемке. Для решения этой проблемы обычно применяются астроинерциальная система определения углового положения спутника и силовой гироскопический комплекс на основе избыточного числа гиродинов [1]. Между тем в космической технике оптико-электронного наблюдения известен принципиально другой способ стабилизации движения изображения. Он основан на применении в оптической схеме телескопа компенсатора движения изображения (КДИ), изменение положения которого приводит к смещению лучей, формирующих изображение. Для космических телескопов наиболее рациональным является

КДИ в виде плоского зеркала, расположенного вблизи фокальной плоскости (ФП) телескопа [2]. При совместной работе (i) СУО спутника и (ii) встроенной в телескоп системы стабилизации движения оптического изображения требуемая точность достигается нониусным способом: I каскад – стабилизация углового движения объектива телескопа, II каскад – стабилизация движения изображения в ФП телескопа [3,4].

В статье впервые исследуется система стабилизации скорости движения изображения (СДИ), встроенная в орбитальный телескоп, который применяется для сканирующей оптикоэлектронной съемки наземных объектов. Здесь принципиальные проблемы состоят в синтезе алгоритмов обработки сигналов для офсетного гидирования по скорости изображения в центре фокальной плоскости телескопа, в разработке математической модели привода для прецизионных перемещений КДИ и алгоритмов цифрового управления.

СИСТЕМА СТАБИЛИЗАЦИИ СДИ

Используются стандартные системы координат (СК) – инерциальная (ИСК) с началом в центре Земли, геодезическая гринвичская (ГСК), горизонтная (ГорСК) с эллипсоидальными геодезическими координатами L, B и H , орбитальная (ОСК) и связанная с КА (ССК) системы координат с началом в его центре масс O . Вводятся телескопная СК (ТСК, базис S ) с началом в центре оптического проектирования S , СК поля изображения Oixi yizi (ПСК, базис F ) с началом в центре Oi ФП телескопа и визирная СК (ВСК, базис V) с началом в центре Ov центральной матрицы ОЭП.

При стандартных обозначениях, принятых в оптических телескопах [5], на рис. 1 представлена схема Ричи-Кретьена, дополненная КДИ в виде плоского диагонального зеркала, которое расположено в сходящемся пучке лучей вблизи ФП объектива. Основная идея встроенной в телескоп системы стабилизации СДИ на поверхности ОЭП с ВЗН приведена на рис. 2. Здесь в объективе 1 телескопа по схеме Ричи-Кретьена дополнительно имеются:

• .    КДИ 2 в виде плоского качающегося диагонального зеркала;

• .    датчик офсетного гидирования (ДОГ) 3 по скорости движения изображения в центре фокальной плоскости (отмечено красным цветом), который реализуется с помощью цифровой обработки сигналов от четырех эталонных ОЭП с ВЗН (помечено синим цветом), которые закреплены в четырех углах единой матрицы ОЭП с ВЗН в ФП телескопа;

• .    преобразователь 4 цифровых сигналов, поступающих на привод 5;

• .    привод 5, обеспечивающий угловые перемещения КДИ 2.

  

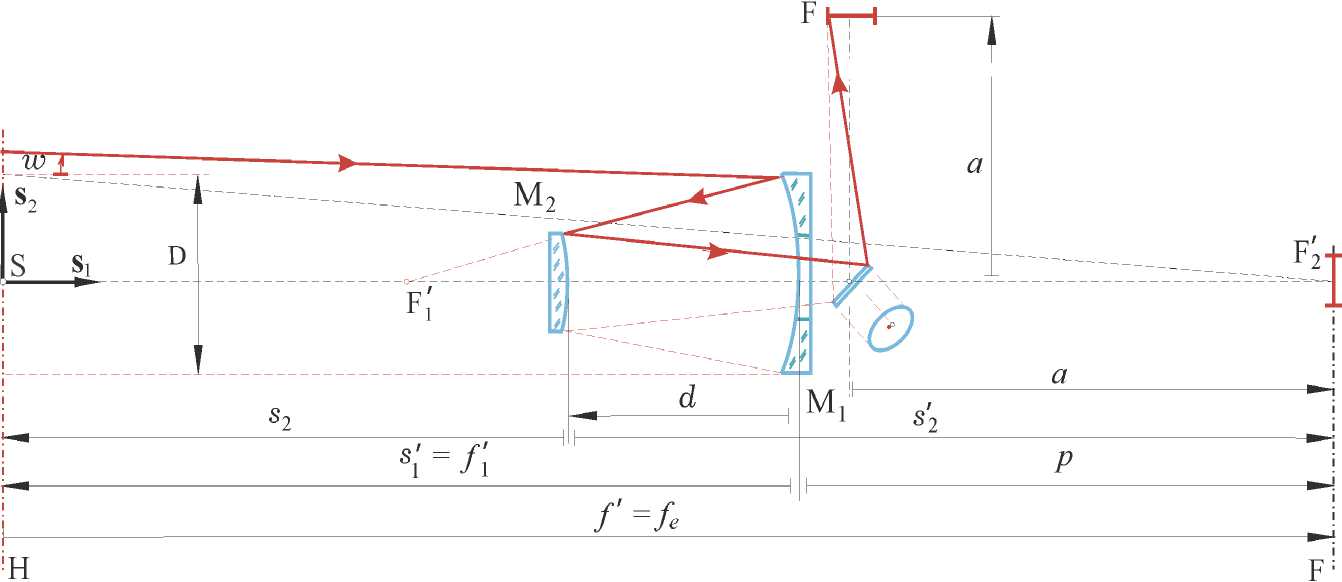
  Рис. 1. Оптическая схема телескопа с компенсатором движения изображения

  
  
  

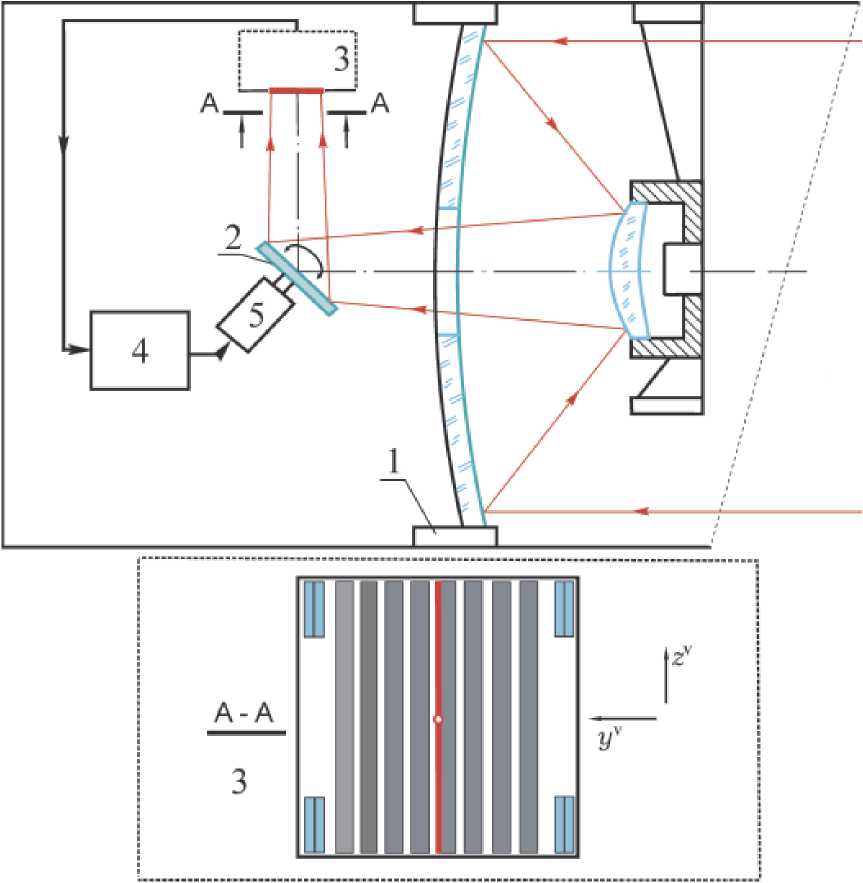
  Рис. 2. Схема системы стабилизации СДИ в фокальной плоскости телескопа

  
  
  

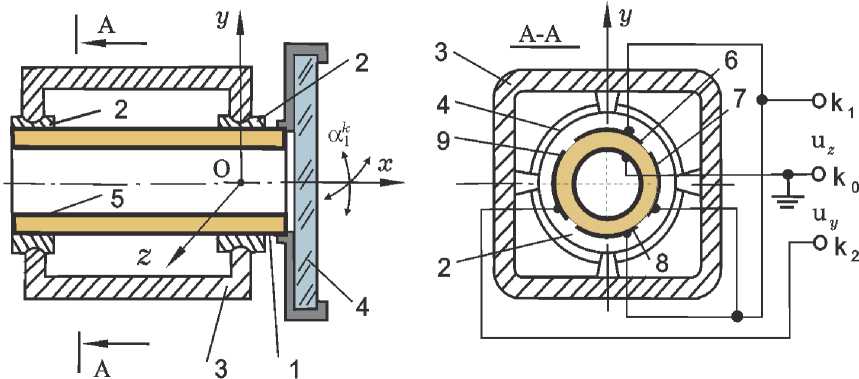
  Рис. 3. Схема пьезокерамического привода КДИ

  
  

  На рис. 3 представлена схема разработанного пьезокерамического привода КДИ [6], который имеет трубчатую конструкцию с возможностью изгиба в двух ортогональных плоскостях и содержит пьезокерамический элемент (ПКЭ) (1), эластичные прокладки (2), корпус (3) и КДИ (4) – плоское зеркало.

  С помощью прокладок (2) ПКЭ свободно закреплен по краям к корпусу (3) в двух ортогональных плоскостях. КДИ (4) жестко закреплен на конце ПКЭ (1) так, что его отражающая плоскость ортогональна оси ПКЭ. Трубчатый ПКЭ имеет пять электродов: общий электрод (5) на его внутренней поверхности и 4 внешних электродов (6) – (9), расположенных вдоль ПКЭ так, что плоскости симметрии противоположных электродов являются ортогональными.

  Продольные части ПКЭ имеют противоположные направления радиальной поляризации под противоположными электродами. При подаче управляющего напряжения на клеммы k 1 л k₀ (или клеммы k₂ л k₀ ) участки ПКЭ под электродами 6 л 8 (соответственно под электродами 7 л 9 ) за счет обратного поперечного пьезо-эффекта деформируются в противоположных направлениях и поэтому ПКЭ изгибается только в соответствующих плоскостях. Следовательно, трубчатый ПКЭ на рис. 3 является эквивалентом управляемого шарнира Гука с двумя степенями свободы.

  В процессе работы описанной системы обеспечивается прецизионная стабилизация продольной и поперечной скоростей движения оптического изображения в центре фокальной плоскости с автоматической компенсацией нестабильности частоты передачи накапливаемых зарядов вдоль столбцов информационных ОЭП, которые отмечены серым цветом на рис. 2.

  ПОСТАНОВКА ЗАДАЧ

  Задачи статьи состоят в синтезе основных алгоритмов обработки сигналов для офсетного

  
  

  гидирования по скорости изображения в центре ФП телескопа, в анализе особенностей модели пьезокерамического привода для перемещений КДИ, в описании алгоритмов цифрового управления этим приводом, а также в представлении численных результатов для оценки эффективности системы прецизионной стабилизация СДИ в центре ФП телескопа.

  
  

  АЛГОРИТМЫ ДОГ

  
  

  Пусть векторы ю е и v S представляют в ТСК

  
  

  угловую скорость и скорость движения центра масс КА относительно ГСК, матрица C = | ^у- | определяет ориентацию ТСК относительно ГСК, а скалярная функция D ( t ) является дальностью наблюдения по линии визирования. Тогда для любой точки в ФП телескопа продольная

  
  

  _у    у                     уу

  V y = V y ⁽ У ^,у ) и поперечная V z = V z (у ,^у ) ~; ,У У составляющие вектора-столбца V = { V_y , V z } нормированной СДИ вычисляются по соотно-

  
  

  шению [7]

  
  

  ~ .

  V ⁱ

  
  

  y i у i

  
  

  z

  
  
  
  
  
  

  is

  q ^V e1

  
  

  s

  q ^V e 2

  
  

  -—’ 7 х         ■—- i x

  - У Ю е3 + z Ю 2

  
  

  _-

  
  

  i у s

  q ^V e3 ⁺

  
  

  ^Ю е3 ^{— У}Х 1

  ® e 2 +^ух 1

  
  

  . (1)

  
  

  Здесь y = y / j_e и z = z / f_e являются нормированными фокальными координатами указанной точки, где f_e – эквивалентное фокусное расстояние телескопа (см. рис. 1), скалярная функция q = 1 — ( c ₂ y + c ₃ z )/ c 1 и компоненты вектора ^у ( t ) = {v^.( t ) i = 1,2.3 = 1 ^ 3} нормированной скорости движения центра

  
  

  масс спутника вычисляются по соотношению v^s_ei= v e . ( t )/ d ( t ) .

  Принципиальная возможность определения вектора V ⁱ нормированной СДИ и углового перемещения КА землеобзора непосредственно по космическим снимкам наземных объектов,

  
  

  получаемых в реальном времени при сканирующей оптико-электронной съемке, возникает при наличии не менее двух линеек ОЭП, близко расположенных в ФП телескопа с обязательным перекрытием в направлении продольной СДИ. Авторская методика решения такой задачи кратко представлена в [8]. Четыре эталонные матрицы содержат по две линейки ОЭП, см. рис. 2, что позволяет в каждой из них в реальном времени определять набор значений векторов нормированной СДИ и по методу наименьших квадратов вычислить значения векторов нормированных

  ~ ~ ~

  СДИ V p = {V p , V p } для четырех точек (y p ,^у ) , p = 1 ^ 4 - центров четырех матриц эталонных ОЭП. Отметим, что здесь рационально выполнять

  
  

  параллельные вычисления на индивидуальном микропроцессоре для каждой эталонной матрицы ОЭП. Соотношение (1) представляется в виде {V y , V } = Q ^l + P ^l №, где

  
  

  Q ¹ (У¹ ,^y ) = q

  
  

  si

  ^V e1 y

  
  

  ~s

  ⁺ V e 2

  
  

  si

  ^V e1 z

  
  

  ^—/ e

  ⁺ v s3

  
  

  p ¹^¹ ) =

  
  

  ~i z

  
  

  ~

  
  

  y~ i    - (1 + ( y )²)

  1 + (~ ^l )²    - уУ

  
  

  На основе такого представления (1) для центров четырех матриц эталонных ОЭП с нормированными координатами (y ^ , ^у1 _р ) получается соотношение Q _p = P p to p , где векторы to p = { to p } , Q p = V p - Q ^l (~,~ p ) и матрица P p = P ^l ( y p ,~ p ) . В совокупности для центров всех четырех матриц эталонных ОЭП получается матричное соотношение Q ^l _s = P ^ to p ,где столбец Q ; = { Q p } и прямоугольная матрица P j = { P p } .

  Оценка to S вектора угловой скорости КА непосредственно по космическим изображениям наземных объектов вычисляется по методу наименьших квадратов как со р = ( P ^ ) # Q ^ , где ( P ^. ) # – псевдообратная матрица в отношении матрицы

  
  

  P j . Оценка (O s используется для вычисления вектора V™ = {V y^ , V_z^l ^ m } в виде ^y m      y s s     s    ~ s     s

  ^V o = ^{{ q V}e2 - ^to e3 ’ q ^Ve3 ^+to e2^{} .    (2)}

  СДИ в центре (; y 0 = 0,^{y l}₃ = 0 ) матрицы информационных ОЭП (см. красную линию в фокальной плоскости телескопа и её центр на рис. 2) на основе анализа космических изображений наземных объектов, поступающих в реальном времени. Вектор V^l₀ ^m (2), сформированный по кратко представленному здесь алгоритму, представляет выходной сигнал ДОГ – вектор измеренной СДИ в центре ФП при фиксированном номинальном угловом положении КДИ.

  МОДЕЛИРОВАНИЕ ФИЗИЧЕСКОГО ГИСТЕРЕЗИСА ПЬЕЗОПРИВОДА

  Основная проблема моделирования и исследования динамики пьезопривода связана с гистерезисом пьезокерамики, применяемой в его конструкции при совмещении свойств упругого подвеса КДИ и собственно электромеханического движителя. Фундаментальная проблема нелинейного анализа систем с гистерезисом исследовалась многими авторами [9]. Математическая модель пьезокерамического привода разработана в [10], где физический гистерезис описывается дифференциальным включением с разрывной правой частью. Такая единая модель имеет 6 параметров и позволяет адекватно представлять широкий класс гистерезисных характеристик. В качестве примера на рис. 4 в нормированном виде приведены два вида характеристик физического гистерезиса единой математической модели, где отличаются только три параметра. Нормированная статическая гистерезисная характеристика пьезокерамического привода КДИ в меридиональной плоскости телескопа (рис. 3, управляющее напряжение u _z ) представлена на рис. 5.

  
  
  

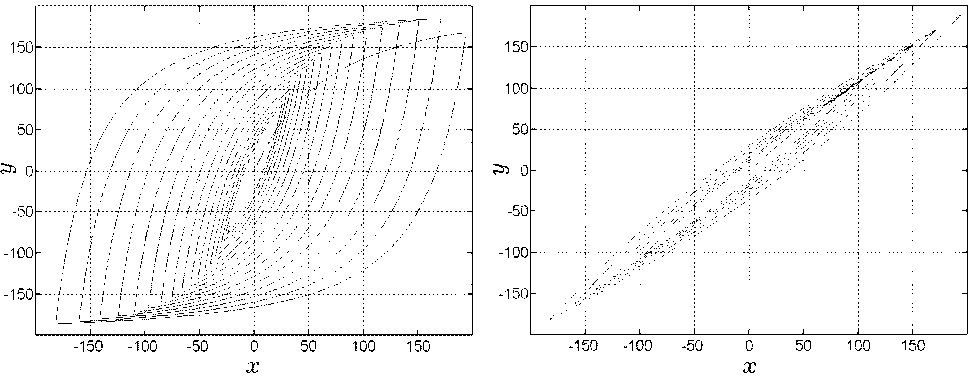
  Рис. 4. Два вида характеристик физического гистерезиса единой математической модели

  
  
  

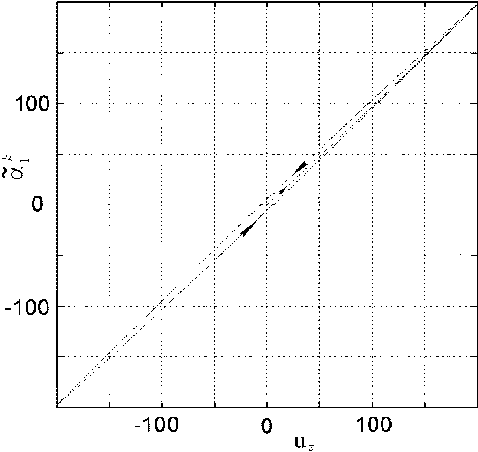
  Рис. 5. Статическая характеристика пьезокерамического привода

  
  
  

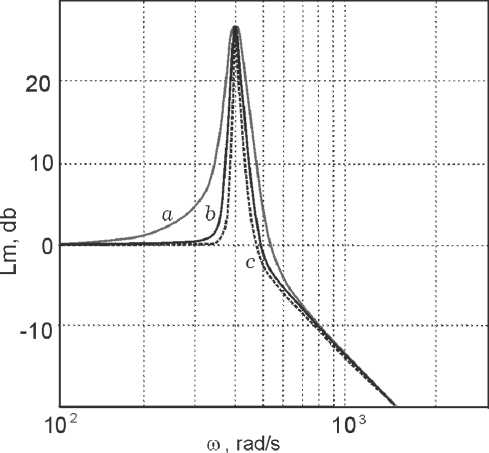
  Рис. 6. Логарифмические амплитудные характеристики моделей пьезопривода

  
  

На рис. 6 приведены нормированные логарифмические амплитудные характеристики двух моделей пьезопривода – линейная модель ( a ) и нелинейная модель ( b ) с идентификацией всех шести параметров гистерезисной характеристики, а также логарифмическая амплитудная характеристика ( c ), построенная на основе экспериментальных данных. Анализ представленных результатов подтверждает приемлемую адекватность разработанной нелинейной модели пьезокерамического привода КДИ с резонансной частотой 63.7 Гц. Как следует из рис. 6, собственные колебательные свойства пьезопривода КДИ практически не проявляются вплоть до частоты 37 Гц.

ДИСКРЕТНАЯ ФИЛЬТРАЦИЯ И ЦИФРОВОЕ УПРАВЛЕНИЕ

~       ~_- ~_-        ~_-

Пусть вектор   V* = {Vy*,Vz*} = {Vyl*,G} является вектором заданной нормированной СДИ в центре ФП телескопа, а вектор Vlo = {Vyo, Vo} представляет фактическую скорость движения изображения в этой же точке ФП. При фиксированном номинальном угловом положении КДИ вектор AV1 погрешности стабилизации СДИ в центре (~‘0 = G,~i = G ) матрицы информационных ОЭП (см. красную линию на рис. 2) формируется по соотношению AVl = V - Vi = {Avy, AVlz} = {AVi, Vzi} , . ~,- ~,- ~,-       ~- ~- где A Vy = Vyo - Vy* и Vz = Vzo. Если же угловое положение КДИ изменяется с помощью его пьезокерамического привода, то вектор 5AVl = {5A V1,5 VZ} погрешности стабилизации СДИ в центре ФП формируется с учетом таких подвижек КДИ и коэффициентов оптической редукции. При этом алгоритмы ДОГ и вектор заданной нормированной СДИ 'V* позволяют вычислить вектор 5VlOm погрешности (рассогласования) СДИ в центре ФП с учетом работы встроенной в телескоп системы стабилизации СДИ. Нетрудно убедиться, что данная система является замкнутой – измеренное рассогласование СДИ поступает на пьезопривод КДИ, изменение положения которого приводит к устранению указанного рассогласования одновременно как в ДОГ на основе цифровой обработки сигналов эталонных матриц ОЭП, так и на информационных матрицах ОЭП.

В контуре системы стабилизации СДИ используются дискретная рекуррентная фильтрация векторного рассогласования 5 V ^l _Om с частотой 32 Гц и рекуррентный цифровой закон управления пьезоприводом КДИ с частотой 16 Гц, который с учетом временного запаздывания [11] обеспечивает астатизм первого порядка и ширину полосы пропускания контура 5.7 Гц.

На рис. 7 представлены графики погрешности компонентов вектора нормированной СДИ в центре ФП без включения (синий цвет) и при включении (красный цвет) системы стабилизации СДИ с применением таких обозначений: V i - поперечная СДИ; 5 V Z - погрешность стабилизации поперечной СДИ при включении встроенной систем _~ ы; A V y — рассогласование продольной СДИ; 5A V y, – погрешность стабилизации рассогласования в нормированной продольной СДИ при включении встроенной системы.

Нормированные продольная и поперечная СДИ вычисляются по формулам V y = V y / f e и V \ = V\ / f e , где f e - эквивалентное фокусное расстояние телескопа [м], а V, y и V\- натуральные линейные продольная и поперечная СДИ с размерностью [м/c]. Поэтому нормированные

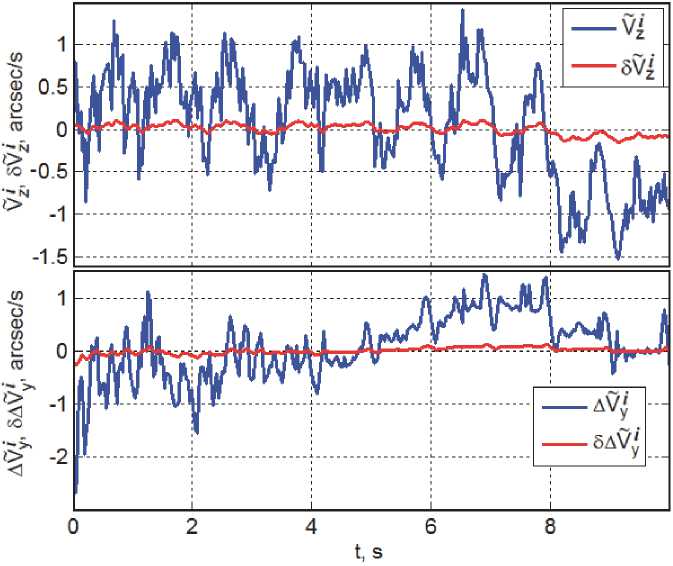
Рис. 7. Графики погрешностей стабилизации компонентов вектора СДИ без включения (синий цвет) и при включении (красный цвет) встроенной системы

СДИ в центре ФП на рис. 7 имеют размерность угловой скорости.

ЗАКЛЮЧЕНИЕ

Научные и научно-технические проблемы углового наведения, высокоточного определения углового положения и управления ориентацией маневрирующих спутников землеобзора общеизвестны, требования по точности стабилизации движения таких КА при сканирующей оптикоэлектронной съемке весьма сложно выполнить традиционными способами.

В статье предложен нониусный способ прецизионной стабилизации скорости движения оптического изображения в ФП орбитального телескопа: I каскад –стабилизация углового движения корпуса телескопа, II каскад – стабилизация скорости движения изображения с помощью специальной оптико-механической системы, встроенной в телескоп.

Выполнен синтез основных алгоритмов обработки сигналов для офсетного гидирования по скорости изображения в центре ФП телескопа, рассмотрены особенности моделирования и исследования статических и динамических характеристик пьезокерамического привода для перемещений КДИ и кратко указаны разработанные алгоритмы цифрового управления с учетом временного запаздывания. Представлены численные результаты, которые подтверждают эффективность предлагаемой системы прецизионной стабилизации СДИ в центре ФП орбитального телескопа.