Прецизионный генератор случайных чисел

Тему разработок, о которых пойдет речь в данной статье, подсказала задача стохастического моделирования. Если модель построена адекватно физическому процессу, то на ней можно проводить численные эксперименты, связанные с изучением поведения объекта или процесса при изменении входных параметров и влияния внешних воздействии. Также немаловажно более глубоко изучить физические и математические связи внутри самого процесса, найти закономерности и установить меру взаимного влияния параметров и переменных объекта, получить новые качественные знания о процессе, восполнить потерянные или неточные данные. Все эти задачи бывает затруднительно, а порой и невозможно изучать на реальном объекте. Понятно, что некоторые ситуации, если их реализовать на практике, потребуют временных и материальных затрат, изменения хода всего процесса или даже режима работы объекта, чего зачастую допустить нельзя. Именно в таких случаях важность задачи имитационного моделирования становится наиболее значимой. Ведь на модели можно реализовать различные ситуации, в том числе и нетипичные для данного процесса или объекта, и провести наблюдение за его поведением при измененных параметрах входа или зависимостях интересующих исследователей показателей.

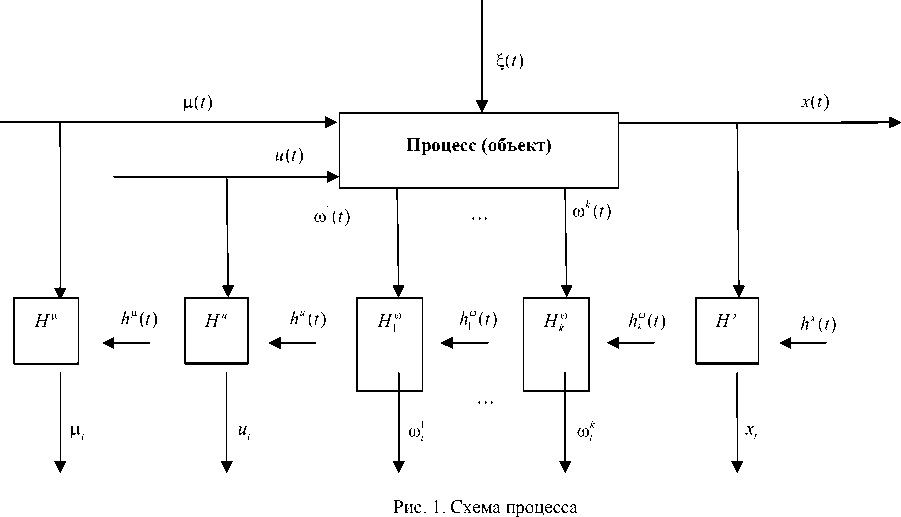
Ниже предлагается общая схема процесса, принятая в теории идентификации [1] (рис. 1). Здесь приняты следующие обозначения: x(t) – векторная выходная переменная процесса; u(t) – векторное управляющее воздействие; ц(t) - векторная входная переменная процесса; юi (t): i = 1,2,..., k - переменные процесса, контролируемые по длине объекта; £(t) -векторное случайное воздействие; t, заключенное в круглые скобки, – непрерывное время; H со значком вверху – каналы связи, соответствующие различным переменным и включающие в себя средства контроля, приборы для измерения наблюдаемых переменных; значок t внизу переменных x, ю, и, ц означает дискретное время; h(t) – со значком вверху – случайные помехи измерений соответствующих переменных процесса. Контроль переменных x, ю, и, ц осуществляется через интервал времени At, т. е. xi,ю^,..., ю2, и, цi, где i = 1, 5 - выборка измерений переменных процесса       (x1, ю1,..., wk, и,, ц1),

( x 2 , ю 2 ,..., ю 2 , и 2 , Ц 2 ) ,..., ( x_s , ю 1 ,..., ю k , u_s , ц 5 ) , ..., здесь s – объем выборки.

Материалы, представленные в данной статье, имеют непосредственное отношение к величинам h ( t ). Речь пойдет о моделировании случайных помех, имеющих определенный закон распределения и числовые характеристики.

Приведем далее некоторые размышления о методе статистического моделирования и его месте в научных исследованиях. Метод статистического моделирования широко используется в разнообразных задачах кибернетики для исследования алгоритмов идентификации, распознавания образов, управления и т. д. В последние годы появилось много эвристических алгоритмов, прежде всего в связи с тем, что новые формулировки задач не поддаются строгой математической постановке. А это, как правило, означает отсутствие процедуры аналитического синтеза тех или иных алгоритмов, доказательство соответствующих теорем сходимости, наличие которых ранее считалось мерой истинности, правильности и основанием того, что дальнейшие действия являются правомерными. В этой связи метод статистического моделирования следует считать доказательным этапом, а не иллюстрацией работы тех или иных алгоритмов. Последнее существенно повышает требования к проведению подобных исследований. Определяющей здесь является возможность повторения определенного цикла численных экспериментов другими исследователями.

Во многих случаях на этом пути безусловно важной является необходимость работы со случайными помехами, распределенными по конкретному закону, а не просто с датчиками случайных чисел, о которых говорят, что они распределены по равномерному, нормальному либо какому-то другому закону. Как оказалось на практике, существующие генераторы случайных чисел весьма условно можно назвать соответствующими заявленным законам распределения. Особенно заметно отклонение на выборках небольших объемов. Все классические алгоритмы генерации [2] верны прежде всего на бесконечно большом объеме выборки, ведь все теоремы сходимости содержат формулировку «Пусть объем выборки стремится в бесконечность» или тому подобное допущение. Однако если объем выборки и достаточен для того, чтобы служить основой для построения модели, то он все равно далек от того, чтобы применить к нему термин «бесконечный». Это говорит о том, что следует задуматься о создании алгоритмов генерации конечной выборки случайной величины и способ создания такой величины будет существенно отличаться от классического подхода. Мы ни в коем случае не спорим с классикой, однако нам хотелось бы больше внимания уделить задачам практики и увязать классический подход с прикладными задачами.

При исследовании многих стохастических процессов предполагается, что плотность вероятности случайных факторов (помех) подчиняется какому-либо закону. В частности, что ошибка измерения электрических и неэлектрических величин электрическими способами подчиняется нормальному закону, в задачах теории надежности используется распределение Вейбулла (интенсивность отказа), логнормальное распределение характерно для многих физических и социально-экономических ситуаций (размер и вес частиц, образующихся при дроблении; заработная плата работника; размеры космических образований; долговечность изделия, работающего в режиме износа и старения, и др.) [3].

Для того чтобы сгенерировать множество случайных точек, свойства которых подчиняются одному из известных законов распределения, необходимо задать закон распределения и его параметры, количественно характеризующие случайную величину, такие как математическое ожидание, среднеквадратическое отклонение, мода и др., и определить количество случайных точек.

Рассмотрим генерацию множества точек для одномерной случайной величины (рис. 2).

Пусть необходимо сгенерировать статистически независимую выборку случайной величины X с плотностью вероятности распределения f ( x , m_x , σ _x , ...). Обозначим через n количество генерируемых точек, т. е. объем будущей выборки. Далее зададим интервал [ a , b ], на котором будет генерироваться выборка.

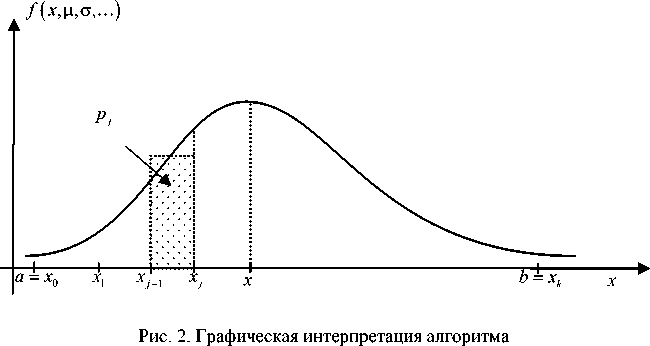
Выборка генерируемых точек должна наиболее полно охватывать всю область возможных значений, но по понятным причинам следует отрезать «хвосты» распределения, где вероятность выпадения значений X становится малой. В этом случае нужно определить этот порядок малости и, например, принять к получению выборки тот интервал, внутри которого f ( x , m_x , ct _x ,...) не меньше некоторого значения. Определим это значение пропорционально f max ^{( x} , m x , ^CT x >-)^:

f ( x = a , m x , CT x ,...) = f ⁽ x = b , m x , CT x ,...) = = ^0,01 - f max ⁽ x, m x , ^CT x ,-У

Для распределений, которые начинаются от x = 0, соответственно примем а = 0, а b получим из вышеприведенных рассуждений. Если границы интервалов не удается определить аналитически, то можно применить любые численные процедуры решения нелинейного уравнения. Для нахождения экстремума распределения также могут потребоваться численные методы, если это невозможно сделать аналитически.

Весь интервал разобьем на множество равных подынтервалов [а = x0,x1,...,xk = b]. Количество интервалов, равное k, будет задаваться пользователем. Внутри каждого подынтервала среднее значение функции плотности определяется по формуле f (xi 1) + f (x,)

^J- 2 j = f ( x j ), (2)

В данном случае качество встроенного генератора случайных чисел становится некритичным.

Совокупность точек, полученных описанным выше способом на всех интервалах, образует выборку случайной величины X , распределенной по заданному закону f ( x , m_x , ct _x ,...), и обладает всеми требуемыми значениями параметров. Выбор точек из представленного набора значений может производиться также любой встроенной функцией извлечения данных из массива значений.

Необходимо проверить, что полученная выборка чисел действительно имеет требуемый закон распределения и обладает нужными характеристиками, для чего по этой выборке строится гистограмма распределения, которая сравнивается с заказанной функцией плотности.

Приведем результаты численного моделирования предложенного алгоритма и оценки характеристик случайной величины по сгенерированной выборке.

Рассмотрим случайную величину, распределенную по логнормальному закону X ~ log N ( ц , ст ² ) , ц = 0, ст ² = 0,5 [ 4; 5 ] . Плотность и закон распределения логнормального закона имеют вид

\- Jl^ ^f ( ^X , ^ц , ^ст) =) V2n X ст

exp

0, X <  0,

(\пХ-ц)"

2 ст ²

V

X >  0,

где x^ [ x j -_, , x j -].

Вероятность попадания случайной величины X в j -й интервал есть площадь, ограниченная функцией плотности на отрезке [ x j - 1 , x j ]. Обозначим ее через p_j :

X

F ( X , Ц , ст ) = J f ( t , ц , ст ) dt .

-да

Оценка плотности распределения, приведенная на рис. 3, построена на основе выборки объемом 5 = 100, количество подынтервалов к = 20. Выборочные

f ( x j - 1 ) + f ( x j )

P ⁽ x - <  X <  x ) = р_; = ------2--⁽ x j ^_ x_H ). ⁽³⁾

На основании закона больших чисел с ростом объема выборки значений случайной величины n частота наступления случайного события стремится к вероятности этого события. Тогда можно принять, что n

P j = -,                    (4)

n где n j – количество попаданий значений случайной величины X в интервал [xj_1, xj- ] из общего объема значений.

Определим количество точек n_j , которые нужно поместить в интервал [ x j _ 1 , x j ] для того, чтобы сгенерированная выборка соответствовала заданному закону распределения (например, равномерному закону или любой встроенной функции генерации конкретного языка программирования):

оценки параметров закона распределения, усредненные по 1 000 экспериментам, составили Ц = - 0,002, CT ² = 0,49.

График, приведенный на рис. 4, построен на основе выборки объемом 5 = 500, количество подынтервалов к = 30. Выборочные оценки параметров закона распределения, также усредненные по 1 000 экспериментам, составили ц = - 0,011, CT ² = 0,497.

Далее рассмотрим случайную величиу, распределенную по двухпараметрическому закону Вейбулла [4; 6]. Этот закон и плотность его распределения имеют вид

F ( X , а , b b )

-f X 1 a

1 - e ^{V b J} , X >  0,

0, X <  0,

I / xa-1 -f X1 a a I — I e Vb ^ X > 0

f ( X , а , b ) = L V b J e , X >  0,     (7)

[ 0, X <  0,

ni = [ Pi' n J .

где a – параметр формы; b – параметр масштаба.

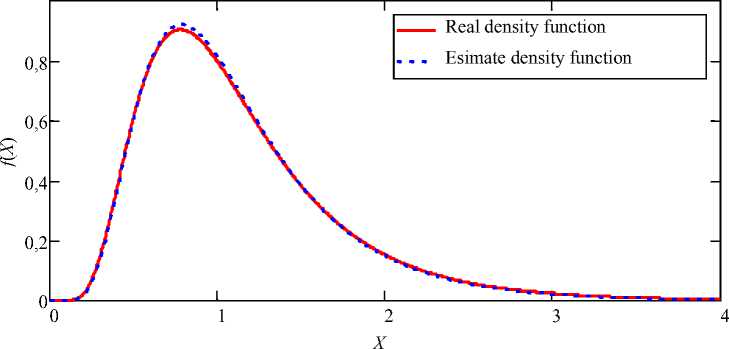
Рис. 3. Плотность распределения логнормального закона и ее оценка: S = 100; k = 20

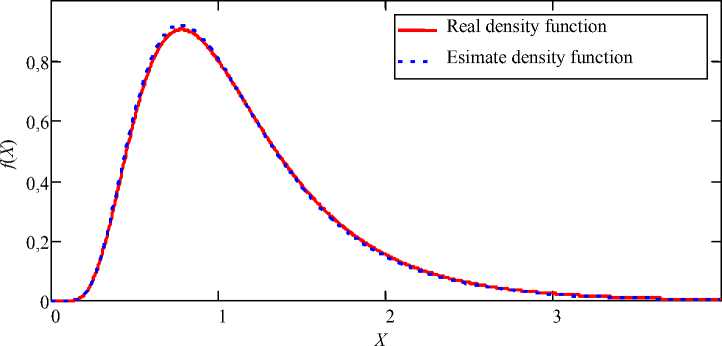
Рис. 4. Плотность распределения логнормального закона и ее оценка: S = 500; k = 30

f ( X )

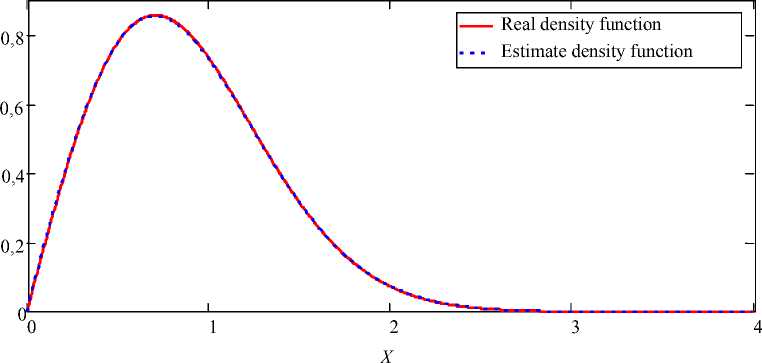
Рис. 5. Функция плотности распределения Вейбулла и ее оценка: объем генерируемой выборки s = 100; количество подынтервалов k = 12; истинные значения параметров a = 2, b = 1; выборочные значения параметров a = 1,991, b = 1

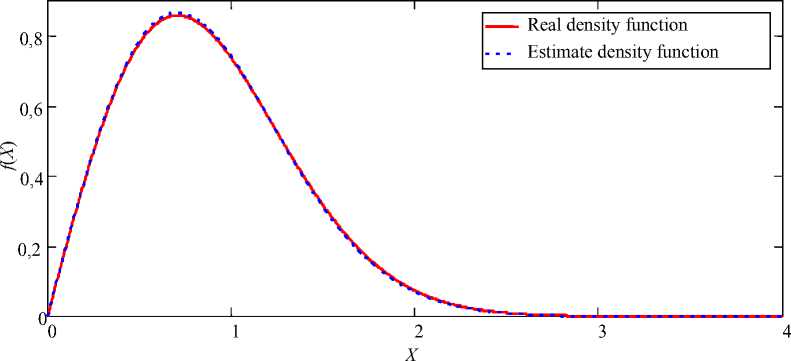
Рис. 6. Функция плотности распределения Вейбулла и ее оценка:

объем генерируемой выборки 5 = 500; количество подынтервалов к = 30; истинные значения параметров a = 2, b = 1; выборочные значения параметров а = 2,012, b = 0,994

В результате проведения экспериментов получены следующие графики (рис. 5, 6).

Построим гистограммы для логнормального распределения (рис. 7, 8) и распределения Вейбулла (рис. 9, 10).

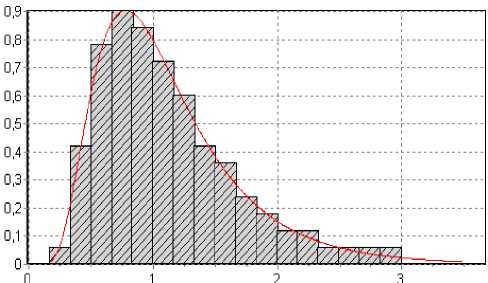
Рис. 7. Гистограмма для логнормального закона: параметры ц = 0, ст ² = 0,5; объем выборки n = 100, количество подынтервалов к = 20

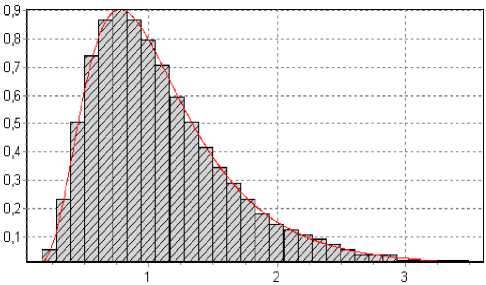
Рис. 8. Гистограмма для логнормального закона: параметры ц = 0, ст ² = 0,5; объем выборки n = 500, количество подынтервалов к = 30

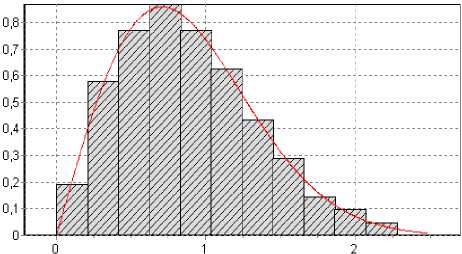
Рис. 9. Гистограмма закона Вейбулла параметры а = 2, b = 1; объем выборки n = 100, количество подынтервалов к = 12

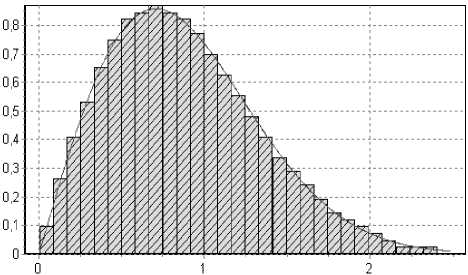
Рис. 10. Гистограмма закона Вейбулла: параметры а = 2, b = 1; объем выборки n = 500, количество подынтервалов к = 30

Дальнейшее развитие исследований касается построения генераторов для как можно большего количества известных функций распределения, изучения свойств сходимости каждого конкретного распределения, точности оценок числовых параметров распределения и случайной величины.