Предельное равновесие вращающихся композитных дисков с трещинами

В данной работе проведено исследование коэффициентов интенсивности напряжений (КИН) и предельного равновесия для композитного диска эллиптической формы, который вращается с постоянной угловой скоростью вокруг его центра.

In hired a study of coefficients of intensity of tensions (SIF) and maximum equilibrium is undertaken for the composite disk of elliptic form with semiaxes, that runs around with an angulator round his center.

В лопастях двигателей, дисках при вращении на высоких скоростях возникают значительные центробежные силы, которые часто приводят к возникновению и дальнейшему росту трещин. В работе детально рассмотрен эллиптический композитный диск, ослабленный внутренней трещиной с вершинами А, В (рис.1). Аналогичная задача для изотропного кругового кольца с трещинами рассматривалась в [4]. .

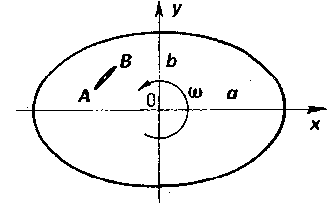
Рис. 1. Эллиптический диск с трещиной при вращательном движении

Напряжение в диске представим у виде суммы: напряжений в сплошном диске (основное решение); напряжений в диске со свободной от нагрузки границей, когда к берегам трещины приложено усилия, равные с противоположным знаком напряжениям, которые возникают здесь в сплошном диске (корректирующее решение).

Напряжение в сплошном диске на основании [3] будут

,   .,1 Г   (г2    Г   2 (G = Р(®а) 7 Ao - + 377-1 + 1

2      a     b        l

- У

- ^^^— —

к

У

к

a2

b2 У J

. 2 £

(

X

y

к (

G y = р ( а ®)- A o 3— + y- - 1 + 1

X2

—-- —

к

a

b

У

к

a

y b2

У

Т

xy

— р ( а ® ) s A o-- , ab

где ап + 2 ах £2 + а22s4

b

£ = —

a

3 ап + (2 а12 + а66) s2 + 3 а2£4 ’

.

Для изотропного материала имеем

_ £4 — 2vs2 + 1

а11 = а 22 = 1/E, а12 = а 21 =—v / E, а 66 = 1/G ^ = 3s4 + 2s2 + 3 , , где ,V модуль Юнга i коэфициент Пуассона.

Корректирующее решение находили разработанным в [1,2] методом интегральных уравнений.

С целью тестирования алгоритма нахождения КИН рассмотрен

— L <  - <  L

,

круговой изотропный диск радиуса R с трещиной параллельной к оси Ох и размещенной на расстоянии y0 от нее.

^FI , II

Рассчитанные относительные КИН

Я = —

^KI , II

^G 0 ^ в

зависимости от относительной длины

R ^— y 0 при V = ^0,3 ,

У о = 0 ⁰         и

3 + v

G =--

у_п = 0,3 R

0   ’      приведены в таблице 1. Здесь

Р ( R ® ) ²            G

- напряжения ^- в центре сплошного диска.

Таблица 1.

Относительные КИН в изотропном круговом диске

X	0,1	0,3	0,4	0,5	0,7	0,8
У о = 0 F i ,	1.0122 (1.0121)	1.1079 (1.1079)	1.1914 (1.1916)	1.3012 (1.3016)	1.6394 (1.640)	1.9367 ( - )
У о = 0,3 R , FI	0.9177 (0.9176)	0.9766 (0.9766)	1.0264 (1.0265)	1.0888 (1.0891)	1.2549 (1.255)	1.3631 ( - )
У о = 0,3 R , FII	0.0048	0.0212	0.0352	0.0539	0.1073	0.1435

В скобках приведено данные из справочника [4], которые получены другим методом. Видно, что полученные разными методами КИН практически совпадают.

Выполнены расчеты КИН для эллиптического диска, изготовленного из изотропного и композитного материала ЛУ-1 с полуосями a, b при b = 0,²⁵ a , когда трещина полудлиной L = ^0,1 a , наклонена под углом ® к оси Ох. Технические упругие постоянные для композитного материала наведены в табл.2, причем в последнем столбце таблицы приведено значение отношения

W„ = E / E E     max    min

,

которое характеризует степень анизотропии материала.

Таблица 2

Упругие постоянные для материала ЛУ-1

Материал	E 1 (Гпа)	E 2 (Гпа)	G 12 (ГПа)	V 21	V 12	W E
ЛУ-1	10,8	96,0	2,61	0,21	0,024	8,89

F

Относительные КИН ^I для более близкой к центру диска вершины для случая, когда центры трещин находятся в точках (0, 25 a , 0)

приведено на рис. 2. Здесь кривым 1-3 соответствуют материалы: изотропный, ЛУ-1 (0), ЛУ-1 (90) (в скобках указано угол между направлением с максимальной жесткостью материала и осью Ох. ).

b / a =0,25

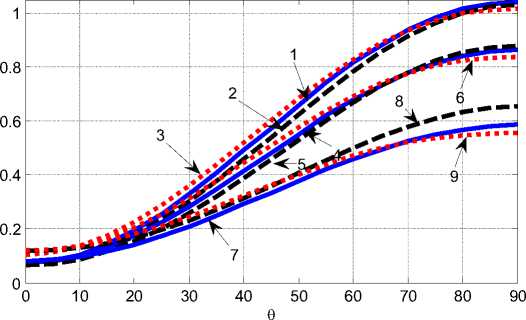
Рис. 2. Относительные КИН для эллиптического диска при вращении

При расчетах введена величина   ° ⁰, которая равна

° напряжению    x в центре сплошного диска, то есть ст0 = 0,5р (та)2 ((1 - A)   .

^{0                  0} ’. Аналогичные результаты для трещин с

(0,5 а ,0)

центрами в точке         изображены кривыми 4-6 и для трещин

(0,75 а , 0)

с центрами в точке          - кривыми 7-9.

Из рисунка 2 видно, что для расмотренных случаев анизотропия материала несущественно влияет на распределение КИН в дисках. Более всего отличаются КИН для материала ЛУ-1 при размещении трещины возле границы ( при размещении центра

(0,75 а ,0) трещины в т. ,   ,

), когда направление с максимальной жесткостью параллельное оси Ох. КИН монотонно возрастают при

0 0

росте угла наклона трещины к большей полуоси от 0 к 90 . Для трещин направленных вдоль большей полуоси диска КИН имеет малые за величиной значения. КИН самые большие для трещин, которые размещенны возле центра вращения и они монотонно уменьшаются при удалении трещины от центра.

Аналогичные результаты для кругового диска приведены на рис. 3.

a / b = 1

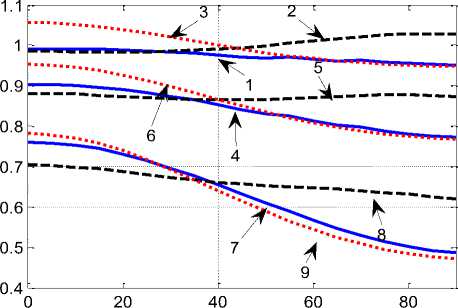
е

Рис. 3. Относительные КИН для кругового диска при вращении

Из рисунка видно, что анизотропия материала для кругового диска существеннее влияет на КИН. Более всего отличаются КИН для материала ЛУ-1 при больших углах наклона трещин, когда направление с максимальной жесткостью параллельное к оси Ох.

Выполнены расчеты предельных нагрузок для изотропного

диска при

b I a = 0,25

для наклоненных под разными углами

трещин, центры которых размещены на большей полуоси в точках

(0,1 ka ,0)

^v ’   ’ ’ при      ^,■■■^, . С этой целью рассчитаны максимальные

обобщенных КИН Ke на наклоненных относительно трещины площадках. На рис. 4 приведено значения относительных значений

F =

Кд а0 JnL

в зависимости от угла наклона трещин при

А = 0,1

где ^А = L ^{1 a} . Аналогичные даные при ^{А 0,2} приведено на рис.

λ=0,1

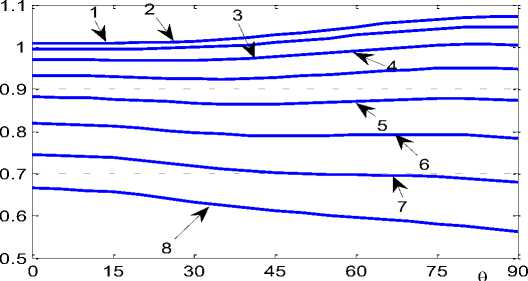
Рис. 4. Относительные обобщенные КИН для диска при X = 0,1

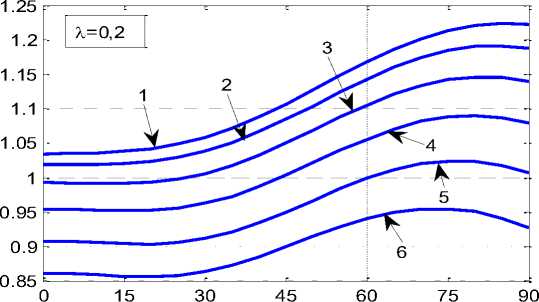
Рис. 5. Относительные обобщенные КИН для диска при X = 0,2

Предельные значения величины о * , определяются по

*    1Y ^ у П - формуле σ =        . Откуда

0     f

о0 =

SK a , де S =

F

Распределение величины S в зависимости от наклона трещины к оси Ох изображено на рис. 6 при X = 0,1 и на рис. 7 при

X = 0,2.

X = 0,1

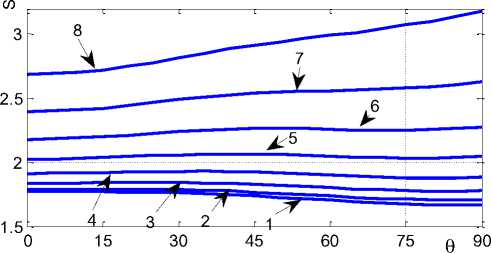
Рис. 6. Предельные значения параметра нагрузки для диска при

Л = 0,1

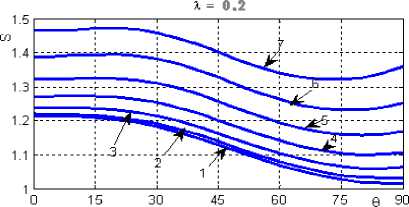
Рис. 7. Предельные значения параметра нагрузки для диска при Л = 0,2

На основании рис. 6 применительно к коротким трещинам ( L / a = 0,1 ) можно сделать следующие выводы относительно предельных значений параметра нагрузки S. Наиболее опасными являются трещины перпендикулярные к большей полуоси диска, при расстояниях центров трещин меньших за 0,5 a . При больших расстояниях к трещинам наиболее неблагоприятными являются трещины, которые параллельные большей полуоси.

При больших длинах трещин L / а = 0,2 предельные значения параметра нагрузки S: являются максимальными и практически постоянными в диапазоне наклонов углов трещины 0 < 6 < 300; монотонно уменьшаются при росте угла наклона трещин в диапазоне углов 30 < 6 < 900, за исключением удаленных трещин (при xc > 0,5a) для которых параметр S имеет локальный минимум. Наиболее опасными с точки зрения разрушения являются трещины, которые перпендикулярные к большей полуоси и находятся на небольших расстояниях их центров (при хс < 0,5a). Для более отдаленных трещин наиболее неблагоприятными являются трещины (при 0 ® 75 — 890). Для всех рассмотренных случаев параметр S монотонно возрастает при удалении трещин от центра диска.

• 1.    Божидарнік В.В. Пружна та гранична рівновага анізотропних пластинок з отворами і тріщинами / В.В. Божидарнік, О.В. Максимович // Монографія. – Луцьк: ЛДТУ, 2003. – С. 226.

• 2.    Божидарник В.В. Напряженное состояние ограниченных композитных пластинок с трещинами при нагружении сосредоточенными силами / В.В. Божидарник, О.В. Максимович // Сборник материалов 2-ой Международной научнотехнической конференции „Надежность и ремонт машин” – Орел, 2005. – С. 215-222.

• 3.    Лехницкий С.Г. Теория упругости анизотропного тела / С.Г. Лехницкий // М.: Наука, 1977. – С. 416.

• 4.    Справочник по коэффициентам интенсивности напряжений. В 2-х томах / Под ред. Ю. Мураками // М.: Мир, 1990. – Т. 1. – С. 448.