Предельное состояние бетонных и железобетонных стержней при сложном и продольно-поперечном изгибе
Автор: Немировский Ю.В., Тихонов С.В.
Статья в выпуске: 1, 2020 года.
Бесплатный доступ
В работе рассматриваются стержни постоянного поперечного сечения. Закон деформирования каждого слоя стержня принят в виде аппроксимации полиномом второго порядка. Изложена методика определения коэффициентов указанного полинома и предельных деформаций при сжатии и растяжении материала каждого слоя на основе наличия трех традиционных характеристик: модуля упругости, предельных напряжений при сжатии и растяжении. На основе диаграмм деформирования бетонов марок B10, B30, B50 при растяжении и сжатии указанные коэффициенты определены методом наименьших квадратов. Проведено сравнение диаграмм деформирования бетонов указанных марок на основе аппроксимаций, полученных по предельным значениям и методом наименьших квадратов, и установлено, что указанные диаграммы достаточно хорошо приближают реальные диаграммы деформирования при деформациях, близких к предельным. Основной задачей в данной работе является определение возможности стержня выдержать приложенные нагрузки, до начала интенсивных процессов трещинообразования в бетоне. Поэтому в качестве критерия условного предельного состояния в данной работе принимается достижение в одном или нескольких слоях стержня максимальной деформацией предельно допустимого значения при растяжении или сжатии, соответствующих на диаграмме деформирования точкам перехода к ниспадающей ветви. При деформировании стержня предполагаются справедливыми классические кинематические гипотезы Кирхгофа - Лява. Рассмотрены случаи статически определимой и статически неопределимой задачи изгиба стержня. Показано, что в случае статически определимых нагружений общее решение задачи сводится к решению системы трех нелинейных алгебраических уравнений, корни которых с необходимой точностью можно получить с помощью хорошо разработанных методов вычислительной математики. Для статически неопределимых задач общее решение проблемы сводится к получению решения системы трех нелинейных дифференциальных уравнений для трех функций - деформации и кривизн. Для приближенного решения этого уравнения на отрезке по длине стержня используется метод Бубнова - Галеркина и рассматриваются конкретные примеры его применения к системе символьных вычислений Maple.
Сложный изгиб, продольно-поперечный изгиб, стержень, предельная деформация, бетон, железобетон, диаграмма деформирования бетона, растяжение, сжатие, метод бубнова - галеркина, системы нелинейных алгебраических уравнений, системы нелинейных дифференциальных уравнений, система символьных вычислений maple
Короткий адрес: https://sciup.org/146281981
IDR: 146281981 | УДК: 539.375 | DOI: 10.15593/perm.mech/2020.1.05
The limit state of concrete and reinforced concrete rods at complex and longitudinal-transverse bending
The work considers rods with a constant cross-section. The deformation law of each layer of the rod is adopted as an approximation by a polynomial of the second order. The method of determining the coefficients of the indicated polynomial and the limit deformations under compression and tension of the material of each layer is described with the presence of three traditional characteristics: modulus of elasticity, limit stresses at compression and tension. On the basis of deformation diagrams of the concrete grades B10, B30, B50 under tension and compression, these coefficients are determined by the method of least squares. The deformation diagrams of these concrete grades are compared on the basis of the approximations obtained by the limit values and the method of least squares, and it is found that these diagrams approximate quite well the real deformation diagrams at deformations close to the limit. The main problem in this work is to determine if the rod is able withstand the applied loads, before intensive cracking processes in concrete. So as a criterion of the conditional limit state this work adopts the maximum permissible deformation value under tension or compression corresponding to the points of transition to a falling branch on the deformation diagram level in one or more layers of the rod. The Kirchhoff-Lyav classical kinematic hypotheses are assumed to be valid for the rod deformation. The cases of statically determinable and statically indeterminable problems of bend of the rod are considered. It is shown that in the case of statically determinable loadings, the general solution of the problem comes to solving a system of three nonlinear algebraic equations which roots can be obtained with the necessary accuracy using the well-developed methods of computational mathematics. The general solution of the problem for statically indeterminable problems is reduced to obtaining a solution to a system of three nonlinear differential equations for three functions - deformation and curvatures. The Bubnov-Galerkin method is used to approximate the solution of this equation on the segment along the length of the rod, and specific examples of its application to the Maple system of symbolic calculations are considered.
Текст научной статьи Предельное состояние бетонных и железобетонных стержней при сложном и продольно-поперечном изгибе
ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2020PNRPU MECHANICS BULLETIN
Активное развитие массового жилищного строительства требует расширения промышленной номенклатуры строительных материалов и конструкций, применения новых технологий в строительстве и создания новых долговечных и экономически эффективных строительных конструкций. В настоящее время наиболее эффективными элементами несущих конструкций для каркасов жилищных и индустриальных элементов являются железобетонные стержневые элементы. Железобетон находит широкое применение в строительстве из-за своих физико-механических свойств, достаточной распространенности ресурсов для его получения, относительно невысокой стоимости изготовления.
Существенное улучшение качества изделий на бетонной основе может быть достигнуто за счет использования армирующих элементов, которые имеют металлическую, полимерную или каменную природу, а также каучукобетонов и полимербетонов [1–3, 7, 8, 26, 28, 29].
Одной из задач при изготовлении стержневых элементов является задача экономии расхода и стоимости материалов. Это обстоятельство вызывает необходимость разработки единого подхода к расчету и анализу поведения гибридных конструкций с различными симметричными и несимметричными профилями поперечных сечений и разными структурами армирования. Методика расчета таких конструкций должна позволять решать задачи при варьировании условий закрепления, загружения, конструктивных форм сечений и параметров армирования. Для конструкций, работающих в условиях плоского изгиба, соответствующие решения были получены в работах [1, 3, 7, 9, 12, 20–23, 24, 25, 27]. При решении практических задач часто возникает задача определения прочности конструкций при совместном действии нескольких силовых факторов. Теория железобетона, базирующаяся на экспериментальном исследовании простых элементов, зачастую не позволяет оценить несущую способность элементов конструкции произвольного сечения при произвольном воздействии силовых факторов [19].
1. Методика решения
В данной работе будем учитывать важное свойство бетонных конструкций – существенно различные закономерности их деформирования в условиях растяжения и сжатия. Бетоны и пластики (армированные и неарми- рованные) при растяжении ведут себя как линейноупругие, в то время как при сжатии диаграммы демонстрируют существенную нелинейность даже при низких уровнях нагружения. Следовательно, как и в работах [1, 3], в различных зонах сечений следует использовать единообразные, достаточно простые аппроксимации диаграмм деформирования с различными (по зонам) коэффициентами. Тогда связь между напряжениями σ , де- n формациями ε в i-й зоне сечения стержня S= ∑ Si i=1
(рис. 1) представим в форме
O i = A i E + A 2 i E2 , (1)
где A , A – экспериментально найденные коэффициенты материалов i -го слоя (зависящие от структуры слоя и свойств фазовых материалов).
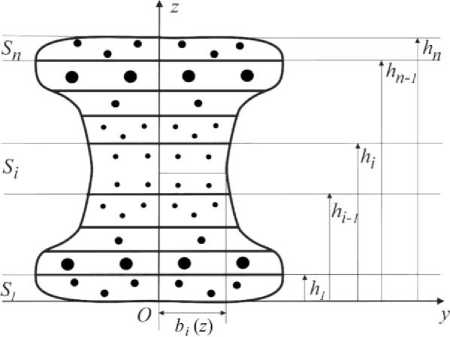
Рис. 1. Поперечное сечение многослойного стержня
Fig. 1. The cross-section of the multilayered rod
Потеря эксплуатационных качеств армированных бетонных конструкций, как отмечается во многих экспериментальных исследованиях [1, 2, 7–11], характеризуется предельными деформациями ( ε- ) при сжатии и ( ε+ ) при растяжении. Их превышение обычно приводит к интенсивным процессам трещинообразования [10, 11], которое в данном исследовании не рассматривается. Тогда в качестве критерия условного предельного состояния в i -м слое принимается достижение в нем максимальной деформации предельно допустимого значения при растяжении или сжатии, т.е. зависимости (1) определяются на отрезке -ε-≤ ε ≤ ε+.
Для определения коэффициентов A , A необходимо, чтобы расчетная модель (1) наилучшим образом соответствовала данным эксперимента в интересующей области деформирования, которую из рассматриваемого круга задач будем считать близкой к предельным состояниям.
При наличии диаграмм растяжения-сжатия бетонов каждого слоя эти коэффициенты можно получить, например, методом наименьших квадратов. При отсут- ствии указанных диаграмм значения искомых коэффициентов и предельных деформаций можно получить, взяв за основу достаточно простые предположения [13]:
-
е + =°+- , E-= 2 ° --, A = E , A^ = 1 E i -, (2) i E i i E i 2 i 4 o4
где о + , o — - пределы прочности бетона при растяжении и сжатии образцов i -го слоя; E – модуль упругости бетона i -го слоя.
Таким образом, при использовании аппроксимации (1) достаточно иметь три традиционных характеристики при рассматриваемом подходе - E , o - , о + .
Результаты расчета коэффициентов A , A по соотношениям (2) для марок бетона B10, B30, B50 по экспериментально найденным предельным значениям E , о - , о + , полученным в [14, 23], приведены в табл. 1. Эти же коэффициенты, определенные методом наименьших квадратов, на основе действительных диаграмм деформирования, полученных в [14, 23], приведены в табл. 2.
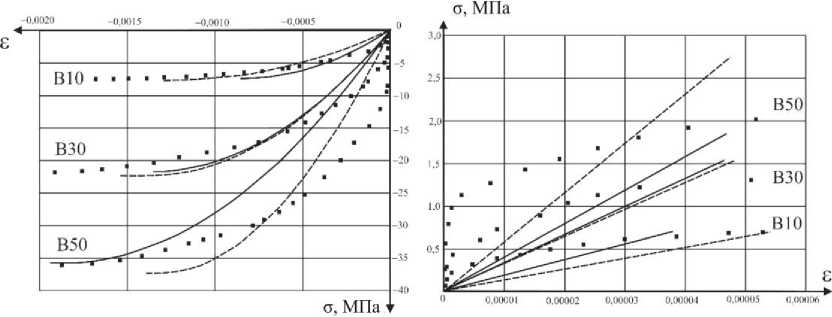
Сравнение диаграмм деформирования, построенных по аппроксимирующим формулам (1), коэффициенты которых определялись методом наименьших квадратов и по соотношениям (2), с экспериментальными диаграммами приведено на рис. 2. Из рисунка видно, что экспериментальные диаграммы достаточно хорошо приближают решение при деформациях, близких к предельным.
Таблица 1
Результаты расчета коэффициентов аппроксимации по предельным значениям
Table 1
The computations of the approximation coefficients based on the limit values
|
Класс бетона |
E , МПа |
о. , МПа |
σ+ , МПа |
ε- , % |
ε+ , % |
A i , МПа |
A , МПа |
A , % |
|
B10 |
17 800 |
7,48 |
0,68 |
0,084 |
0,0038 |
17 800 |
10 589 572 |
38,89 |
|
B30 |
32 200 |
21,8 |
1,44 |
0,135 |
0,0045 |
32 200 |
11 890 367 |
38,24 |
|
B50 |
38 600 |
35,9 |
1,84 |
0,186 |
0,0047 |
38 600 |
10 375 766 |
44,63 |
Таблица 2
Результаты расчета коэффициентов аппроксимации методом наименьших квадратов. A – средняя ошибка аппроксимации
Table 2
The calculation results of the least squares approximation coefficient A an average approximation error
|
Класс бетона |
A , МПа |
A , МПа |
A , % |
|
B10 |
12 488 |
5 078 524 |
33,26 |
|
B30 |
32 351 |
11 660 358 |
38,14 |
|
B50 |
56 490 |
21 305 730 |
39,29 |
а
б
Рис. 2. Диаграммы сжатия ( а ), растяжения ( б ) бетонов, построенные методом наименьших квадратов (сплошная линия) и по предельным значениям (штриховая линия). Квадратами обозначены точки экспериментальной диаграммы
Fig. 2. Diagrams of a) compression, b) tension of concrete constructed by the least squares method (solid line) and by limit values (dashed line), the squares indicate the points of the experimental diagram
Выберем декартову систему координат с осью x , направленной вдоль оси стержня, с определенной привязкой к поперечному сечению и с началом координат на одном из концов стержня.
Для упрощения получающихся в дальнейшем формул будем считать, что структуры гибридных армированных стержней и распределения внешних нагрузок согласованы так, что в процессе деформирования эффекты закручивания либо вовсе не возникают, либо столь незначительны, что ими можно пренебречь. Тогда возникающие поля напряжений о. будут порождать внутренние силовые факторы:
nnn
N=E J ^dS, My=E J ^-zdS, Mz =-E J ^ydS,(3)
i =1 s. i =1 i =1 s.
iii
В случае статически определимых стержней значения N (0), Qy (0), Q (0), Mz (0), My (0) определяем из условий равновесия крайних узлов. Для статически неопределимых задач необходимо будет составлять дополнительные условия совместности деформаций.
Используя классические кинематические гипотезы Кирхгофа – Лява, для деформаций будем иметь выражения [15]
e( x , y , z ) = E 0 ( x ) - y к z ( x )+ z к y ( x ), (6)
, _ dun d 2 wn d 2 vn
£0( x) = 0, к y = —/, к z = —^, dx dx dx
которые должны удовлетворять уравнениям равновесия [15]:
d2 Mz _ dmz dx2 qy dx ’
d 2 M y dm y dN
~i=~ = qz-^r , dx dx dx
- q x • (4)
Здесь N – проекция вектора внутреннего усилия на ось x ; Mz , My - проекции вектора внутреннего момента на оси z и у . Величины qx , qy , qz - проекции вектора распределенной нагрузки приложенного к оси стержня; mz , my - проекции вектора распределенных моментов на оси z и y .
Интегрируя уравнения (4), получим:
где u 0, v 0, w0 - компоненты вектора перемещений точек осевой линии стержня.
Из соотношения (6) можно получить уравнение нейтральной линии для каждого поперечного сечения стержня:
£ 0 ( x ) - y к z ( x ) + Z к y ( x ) = 0.
Интегрируя соотношения (7), получим:
u 0( X ) = u 0
u 0 ( x ) = U 0
x
(0) + J s0 ( x ) dx , 0
(0) + фу (0) x + J J к ( x ) dx dx ,
xx
0 L 0
xx
H -0( x ) = И -0
(0) + ф2 (0) x + J J к ( x ) dx dx , 0 L . y J
N ( x ) = N (0) - J q^dx ,
xx
Ф y ( x ) = ф y (0) + Jк z ( x ) dx , Ф z ( x ) = ф z (0) + Jк y ( x ) dx . (9)
0 0
x
M z ( x ) = M z (0) - Q y (0) x - J mzdx +
x
x
x
j J q dx dx , (5)
0 . . y J
M y ( x ) = M y (0) - Q z (0) x - J m y dx +
x
x
j j q dx dx .
0 L J. J
Величины u 0 (0), u0(0), w 0 (0), фу(0), ф2 (0) находим из условия закрепления стержня.
Будем считать, что стержень имеет одинаковую форму поперечного сечения вдоль всей длины, причем
контур этой формы полностью определяется системой функций b ( z ), i = 1,.., n (см. рис. 1).
Подставляя выражения (1) в (3) и учитывая реальную структуру расположения материалов в сечении, для величин N , My , Mz получим систему трех равенств в виде полиномов второго порядка от величин е0, к,, кг:
nnhibi ( z )
N=ZJJ ^dS=Z Jdz J ^dy= i=1 S i=1 hi-1 - b( z)
n hi bi ( z )
= Z J dz J (Aue + AA)dy = i=1 hi-1 - bi( z)
n hi bi ( z )
= Z J dz J ( A1i (S0 (x) - Укz (x) + zкУ (x)) + i=1 hi-1 - b (z)
+ A 2 i ( S o ( x ) - У к z ( x ) + z к y ( x ) ) 2 ) =
= f So ( x ) + f • к y ( x ) + f 3 к z ( x ) + f l 1 S 0 ( x ) + f 2 к 2( x ) +
+ f 3K2 (x) + f10S0 (x)кy (x) + n hi 1 n fl.! = Z A2i J z 3 bi( z)dz , f13 = tZ A2 i J zbi (z)dz , i=1 hi-1 3 i=1
n hi 1 n f14 =Z A2 i J z2 bi2( z) dz , f1S =-iZ Ali J b3( z) dz , i=1 hi-1 3 i=1
1 nhi fl6 .Z A2i J bi (z)dz .
4 i=1
В случае статически определимых балок при известных функциях N , My , Mz дальнейшее решение задачи сводится к численному решению системы трех нелинейных алгебраических уравнений относительно трех неизвестных s0 , к , кг и последующему вычислению по формулам (8), (9).
В случае статически неопределимых задач следует подставить выражения (10)–(12) в уравнения равновесия (4) и при учете выражений (7) получить разрешающую систему трех нелинейных дифференциальных уравнений относительно трех неизвестных функций u o( x ) , u o( x ), " ,'. < x ) :
+ f 3 8 » ( x ) к z ( x ) + f ,3 K y ( x ) к z ( x ), (10)
nnhibi ( z )
M y = ZJJ z s dS = Z J dz J ^ zdy = i =1 s i =1 h -i - b ( z )
= - f ’ S 0 ( x ) + f lo к y ( x ) + fl 1 K z ( x ) -
- 1 f 7 S 0 ( x ) + fl! K 2 ( x ) + fl 3 K 2 ( x ) -
- 2 f M x ) к y ( x ) - f , S o ( x ) к z ( x )+ f 4 K y ( x ) к z ( x ), (11)
d 2 u 0
f 1 dx 2
- f -
—
d 3Uo
2 dx 3
+ 2 f 5
—
f 3 d"Wr + 2 f 4 dx 3
d 2 u 0 d 3u 0 dx 2 dx 3
d 2 u0 d 2u0 dx 2 dx 2
- f -
+ 2 f ,
du d 2 u dx dx 2
d 2 w 0 d 3 w 0 dx 2 dx 3
du0 d 3u0 dx dx 3
- f 8
du d3w dx dx3
d 2 u d 2 w 0 d 3u0 d 2 w 0
f 8 i 2 + f 9 П 1 2
dx 2 dx 2 dx 3 dx 2
nnhibi ( z )
Mz = -ZJJyadS=-Z Jdz J ^-ydy= i=1 S i=1 hi-1 - bi( z)
= f 3 S 0 ( x ) - fll K y ( x ) - f!SK-z ( x ) + 2 f 8S0 ( x ) -
- 1 fl 4 K 2 ( x ) - У 1б К 0 ( x ) + f > S o ( x ) к y ( x ) +
+ 2 f , S o ( x ) к г ( x ) - 2 f H к y ( x ) K z ( x ), (12)
r dг и d 3 wn
+ f '^0^0 = - q x , dx dx 3
d3 u 0 d4 u0
2 1011
dx3 dx4
—
[ d un 1
f 71 j 2 I +
I dx 1
+ 2 f 21 d ^° I + 2 f 31 dW 0 I + 12 213 2
I dx 1 I dx 1
fl =Z/1i J b(z)dz , f2 =-Z Ali J zbi(z)dz , i=1 hH i=1 hH f. =-1 ZZAli J b-( z) dz, f,-УА. it bi(z■) dz,
2 i = 1 h i - 1 i = 1 h i - 1
du0 d 3 u0 d 2 u0 d 4u0
dx dx 3 1 dx dx 4
+ 2 fi 3
n hi n f5 =Z A2i J z 2 bi( z) dz , f, =,Z A2 i J b3( z) dz , i=1 h 3 i=1
hi-1
n hi n f 7 = -2Z A2i J zbi(z)dz , f 8 =-Z A2i J bi2(z)dz , i=1 hi-1 i=1
+ 4 f 5
d w d 4 w dx dx 4
d2u0 d 3u0 dx dx 3
+ 2 f 5
+ 2 f 5
d 3 u0 d 2 u0
dx 3 dx du0 d 4 u0 dx dx 4
+
+
d 3 u 0 d w 0 d u 0 d 3 w 0
dx 3 dx 9 dx dx 3
n f 9 = Z A2i J z6i2(z)dz , i=1
h i - 1
n hi 1 nh fi0 =-ZAli Jz2bi(z)dz, fl 1 =-qZAli J zb2(z)dz, i=1 hi-1 2 i=1
dun d 4 wn d 4vn d 2 wn d 3vn d 3 wn
+ f„ —'---' + f.--- '---' + 2 f.------- ' +
9 dx dx 4 14 dx 4 dx 2 14 dx 3 dx 3
. dг и d4 w0dm,
+f14^°^°=qz- dx2 dx4
d 3 u0 d 4 v0
”5^ - f" ~сьг
d 4 w dx 4
r ( d2 u n I2
f 8 I J 2 I +
I dx 1
/ x 9 /x 9
I d I I dwI
+ f14 I J 2 I + 2 f 16 I j 2
I dx ) I dx
—
+ 2 f 6
du0 d 3 u0 d 2v0 d 4v0
dx dx 3 14 dx 2 dx 4
d 2 w o d 4 w o d 3 u 0 d 2 u o
dx 2 dx 4
dx 3 dx 2
+
+ 2 f 9
d 2 u0 d 3 u du0 d 4 v0
dx 2 dx 3
dx dx 4
+
тогда граничные условия (13), (14) будут удовлетворены, причем изгибающие моменты и продольное усилие в местах защемления стержня будут отличны от нуля.
Подставим разложения (18) в систему (13)–(15) и обозначим в полученной системе разность левой и правой части (13) через L ( x ), (14) – L ( x ), (15) – L ( x ).
Возьмем в качестве базисных функций в методе Бубнова – Галеркина те же функции, что и в разложении (18):
+ A dw + 4 du dw +
6 dx 3 dx 2 6 dx 2 dx 3
fk ( x )
k — 1 k + 1
= cos nx — cos nx, ll
k = 1... N .. (20)
du 0 d4w o d 4u0 d2w o d 3Uo d3w o ,
6 dx dx4 13 dx4 dx2 13 dx3
A £wdm dx2 dx4
Составим систему из 3N алгебраических уравнений относительно 3N неизвестных B, C,D,k = 1... N:
В качестве примера рассмотрим случай стержня, защемленного с обоих концов (рис. 3).
l
J Lt ( x ) f ( x ) dx = o, i = 1...3, k = 1... N . (21)
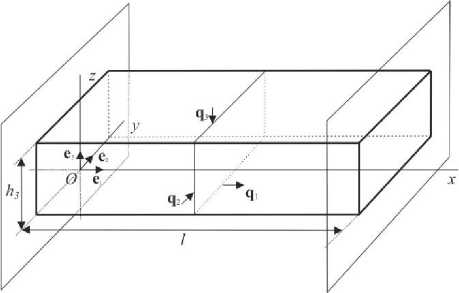
Рис. 3. Стержень длины l , защемленный с обоих концов
Значение искомых коэффициентов B , C , D определим из указанной системы каким-либо численным методом [18]. Значение изгибающих моментов и продольного усилия определяется соотношениями (13)–(15).
Ввиду достаточной громоздкости формул при увеличении количества приближений N и роста погрешности при округлении свободных членов указанное решение задачи удобно искать с использованием системы символьных вычислений, например Maple, которая позволяет получать приближенные аналитические решения [17].
Положим, что длина стержня l = 1o м, количество слоев n = 3 и он имеет двутавровое поперечное сечение с параметрами (см. рис. 1):
Fig. 3. The rod of l length pinched at both ends
Из условий закрепления стержня имеем граничные условия:
A) = U o (O) = w o (o) = u o (l ) = U o ( l ) = w o (l ) = 0, (16)
^( z ) = b o1 = o,4 м, b 2 ( z ) = b o2 = 0,3 м,
1 2 3 (22)
b 3 ( z ) = b03 = o, 4 м, h = - м, h = — м, h = - м.
d u0
dx x = o
dw0 _d u0
dx x = o dx x = l
dw dx
Приближенное решение такой системы можно искать при использовании метода Бубнова – Галеркина [16].
Решение будем искать в виде
Предположим, что в стержне послойно реализованы следующие марки бетона: 5 , — B5o, S2 — B3o, S 3 — B5o, коэффициенты в уравнении (1) определены методом наименьших квадратов (табл. 2).
Пусть на стержень действуют распределенные нагрузки q , q , q (см. рис. 3) вдоль соответствующих граней:
NN uo(x) = EBy(x), uo(x) = ECktk(x), k=1 k=1
N wo(x) =Z Dkrk (x)’ k=1
q 1 = ( t 1 + t 2 x ) e 1 , q 2 =
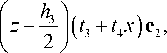
q 3 = ( t 5 + t 6 x ) e 3 ,
тогда проекции этих нагрузок вдоль всей длины стержня имеют вид
где B , C , D – искомые коэффициенты, которые и определяют решение задачи.
Если положить
b 01
q x = J ( t 1 + t 2 x ) dy = 2 b o1 ( t 1 + t 2 x ) ,
— b o1
k — 1 k + 1
yk ( x ) = 1k ( x ) = r ( x ) = cos — n x — cos — n x , (19)
3 hi qy = Z JIz i=1 h~ i ^
—
1 3 + 1 4 x ) dz = ^( 1 3 + 1 4 x ) ( h 1 h 3 + h 2 ) ,
b 03
q z = J ( t 5 + t 6 x ) dy = 2 b03 ( t 5 + t 6 x ) .
-
- b 03
Распределенные вдоль граней нагрузки q , q , q будут вызывать появление распределенного момента по длине стержня, проекция которого определяется соотношениями:
b 03
m y = - J ( 1 5 + 1 6 x ) xdy ,
-
- b 03
-
b 01 3 h k ( h )
mz = - J (t +12 x) ydy + ^ JI z--l( 13 + 14x) xdz,
-
- b 01 k = 1 h k - 1 ^ 2 ^
откуда можно получить my = -2b03 (15 +16 x)x, mz =^( 13x + 14x2)(hh + h2).
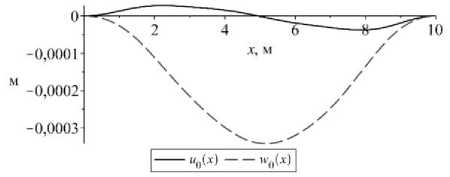
Рис. 4. Изменение величины перемещений защемленного с обоих концов стержня
В результате расчета по соотношениям (18)–(21) в математическом пакете Maple при N = 7, с параметрами
Fig 4. The change in the amount of displacements pinched from both ends of the rod
1 1 = 0, 1 2 =- 2,5 кН/м 3 ,
13 = 0, 14 = 2 кН/м4, 15 = 0, 16 = -3 кН/м3, получаем нелинейную систему алгебраических уравнений относительно неизвестных коэффициентов B ,C ,D , которую решаем численно в этом же пакете методом Ньютона [17, 18], используя для каждого коэффициента в качестве начального приближения нулевое значение. В результате указанного решения получаем приближенные решения вида (18) для перемещений u0(x), u0(x), w0(x) (рис. 4). Найденные выражения для перемещений позволяют по соотношениям (6), (7), (10)– (12) получить аналогичные приближенные решения для деформации и продольного усилия в любом сечении стержня.
Найденные решения будут справедливы в случае, если деформация £ в каждом сечении стержня не превысила свои предельные значения для каждого фазового материала. В противном случае будем считать, что имеем дело с потерей несущей способности стержня.
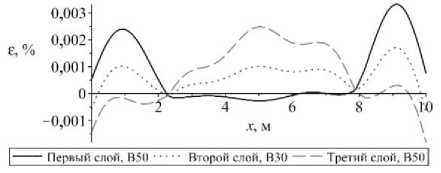
Для того чтобы оценить несущую способность стержня, определим максимальную и минимальную деформацию в каждом сечении стержня для каждого слоя. Учитывая, что выражение для деформации (6) является линейной функцией относительно переменных y , z и что каждый слой в сечении представляет прямоугольник, максимальную и минимальную деформацию в каждом сечении для каждого слоя будем искать как соответственно максимальное и минимальное значение из четырех значений деформации в вершинах прямоугольника, ограничивающих указанный слой. В случае произвольной формы сечения стержня максимум и минимум придется искать вдоль линии, ограничивающей контур каждого сечения. Графики для перемещений приведены на рис. 4, графики деформаций для каждого сечения стержня и каждого слоя – на рис. 5.
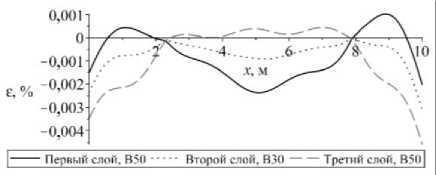
Рис. 5. Изменение величины: а – максимальной; б – минимальной деформации в сечении защемленного с обоих концов стержня
Fig. 5. The change in the amount of displacements pinched from both ends of the rod
Анализируя рис. 5 и табл. 1, можно увидеть, что деформация для каждого слоя в любом сечении не превысила предельные значения. Соответственно, полученное решение справедливо.
В случае, если увеличить продольную нагрузку, положив 1 2 =-12кН/м3, то указанная нагрузка является близкой к предельной в первом слое в сечении, близком к правому концу стержня (рис. 7, а ).
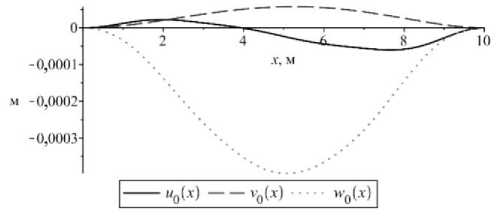
Рис. 6. Изменение величины перемещений защемленного с обоих концов стержня
Fig. 6. The change in the number of displacements pinched from both ends of the rod
б
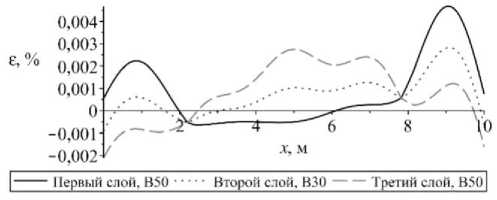
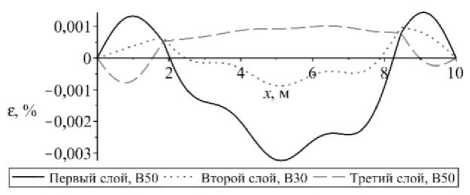
Рис. 7. Изменение величины: а – максимальной; б – минимальной деформации в сечении защемленного с обоих концов стержня
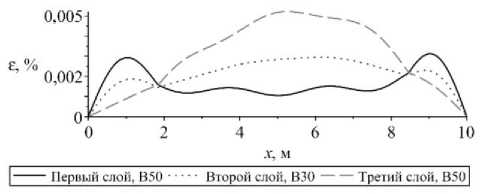
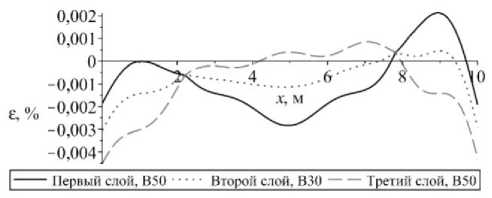
б
Рис. 9. Изменение величины: а – максимальной; б – минимальной деформации в сечении шарнирно-опертого с обоих концов стержня
Fig. 7. The change in the value of a – maximum, b – minimum deformation in the cross section of the rod clamped at both ends
В случае, когда тот же самый стержень шарнирно оперт с обоих концов, в качестве функций y ( x ), t ( x ), r ( x ) в разложении (18) возьмем следующие:
, x k - 1 k + 1
yk (x) = cos —— nx - cos —— nx, k к tk (x) = rk (x) = sin у x,
тогда в местах закрепления стержня перемещения и изгибающие моменты будут равны 0.
Если принять, что на стержень действуют нагрузки, аналогичные предыдущему случаю (23), получим для перемещений и деформаций решения, изображенные на рис. 8, 9. Из рис. 9, а видно, что деформация превысила предельное значение при растяжении в третьем слое в середине стержня. Из рис. 9, б можно заметить, что деформация не превысила предельных значений при сжатии во всех слоях стержня.
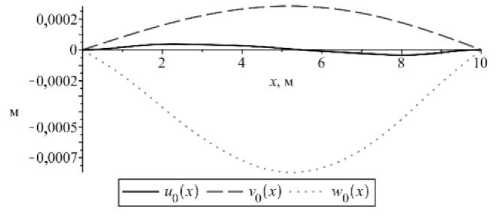
Рис. 8. Изменение величины перемещений в сечении шарнирно-опертого с обоих концов стержня
Fig. 8. The change in the magnitude of the displacements in the cross section of the rod the pivotally supported from both ends
Fig. 9. Change in the value of a ) maximum, b ) minimum deformation in the cross section of the rod pivotally supported from both ends
В пределах принятой формы сечения мы можем изменить несущую способность за счет изменения параметров сечения, а также за счет замены материалов слоя на другие. Например, в случае изменения параметров сечения (22) на значения
b ( z ) = b 01 = 0,4 м, b 2( z ) = b02 = 0,3 м,
117 b (z) = b03 = 0,4 м, h = - м, h = -м, h = — м в условиях тех же самых нагрузок (23) график перемещений и деформаций примет вид, представленный на рис. 10, 11. Как видно из указанных рисунков, деформация в каждом слое не превышает предельных значений.
-o.oooi-
-0,0002
-0,0003
-0,0004
-0,0005-
0,0003
0,0002
0,0001-
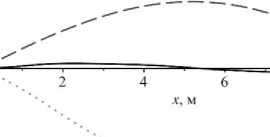
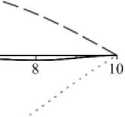
Рис. 10. Изменение величины перемещений в сечении шарнирно-опертого с обоих концов стержня
Fig. 10. Change in the magnitude of displacements in the cross section of a rod pivotally supported from both ends
Тот же самый эффект можно получить, если, например, увеличивать следующие параметры сечения стержня:
Ь ( z ) = b01 = 0,6 м, b 2( z ) = b02 = 0,5 м,
1,2,3 b ( z ) = b03 = 0,6 м, h = - м, h = —м, h = - м.
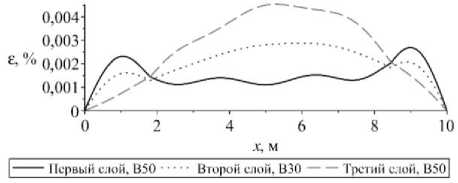
б
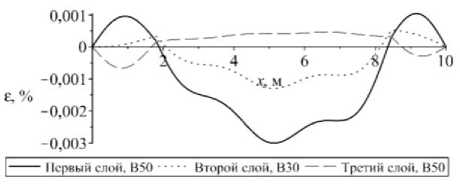
Рис. 11. Изменение величины: а – максимальной; б – минимальной деформации в сечении шарнирно-опертого с обоих концов стержня
Fig. 11. The change in the value of a ) maximum, b ) minimum deformation in the cross section of the rod pivotally supported from both ends
Из рис. 12, 13 видно, что деформация, так же как и в предыдущем случае, не превышает предельные значения.
-0,0001
-0,0002
-0,0003 м -0,0004 0,0005 -0,0006 -0,0007
---"oW--V-0..... ^оМ
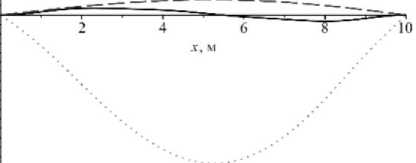
Рис. 12. Изменение величины перемещений в сечении шарнирно-опертого с обоих концов стержня
Fig. 12. The change in the magnitude of displacements in the cross section of a rod pivotally supported from both ends
Выбор подходящего варианта из возможных конфигураций сечения стержня, способных выдержать приложенные нагрузки, может быть обусловлен массой стержня, сложностью изготовления, ценой материалов и т.д.
В случае, когда приложенные усилия к стержню располагаются в одной плоскости, при условии наличия соответствующей симметрии поперечного сечения стержня, имеет место случай плоского изгиба. Рассмотрим для определенности случай продольно-поперечного изгиба в плоскости OXZ (рис. 14), где e,e2,e3 - единичные векторы с началом в начале координат, направленные вдоль осей OX , OY , OZ соответственно.
б
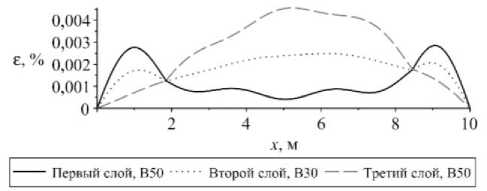
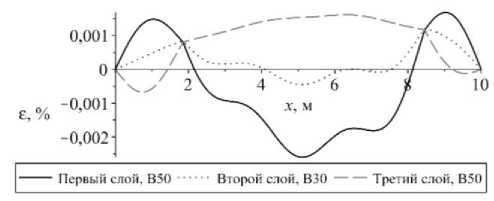
Рис. 13. Изменение величины: а – максимальной; б – минимальной деформации в сечении шарнирно-опертого с обоих концов стержня
Fig. 13. The change in the value of a ) maximum, b ) minimum deformation in the cross section of the rod pivotally supported from both ends
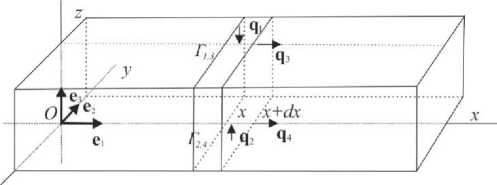
Рис. 14. Случай продольно-поперечного изгиба
Fig. 14. The case of longitudinal-transverse bending
Рассмотрим элемент стержня, выделенный двумя поперечными сечениями с координатами x и x+dx , где dx – достаточно мало.
Обозначим через R главный вектор и M главный момент всех сил относительно начала координат. Причем справедливо
R = R 1 + R 2 , R 1 = JJ о dS , R 2 = E J q k d Y k + EJJ q sk dS k , Sk Г kkSk
M = Mj + M2 , Mj = JJ r X о dS ,
S
M2 =EJr x qkdyk +EJJr X qskdSk, kГk kSk qsk = Pk g = Pk ( gx el + gy e2 + gz e3 ) , где R , M – главный вектор и главный момент внутренних сил; R,, M2 – главный вектор и главный момент внешних сил; σ – вектор напряжения, действующий в соответствующих точках сечения; q – вектор распределенной внешней силы, действующей вдоль кривой Г; q4 - вектор распределенной массовой силы, действующей в сечении к-го слоя стержня; g - вектор ускорения свободного падения; pt - плотность к -слоя стержня.
Положим, что векторы r , о , q , q4 разлагаются в базисе e , e2 , e следующим образом:
r = x e. + y e2 + z e , о = ст, e, + ст, e + ст, e, ,
1 2 3 Л 1 у 2 Z 3
qk = q^x ei+ qky e2+ qz e, qk qskxe + qsky e2 + qskze , откуда получим выражения для главных векторов и моментов:
М 1 =Я ( У % z - z % у ) dS e i +
S
+ Я ( z % x - X % z ) dS e 2 - Я ( У % x — x % y ) dS e 3 ,
SS
M 2 = Z J ( yq >z - zq >y d y k e - Z J ( xq >z - zq ^ ) d y k e 2 + kГ k kГ k
+Z J ( xqy- yq^ d yk e + k Гk
+ZJJ( yqskz- zqs.) dSk e - k Sk
-Z JJ ( xq^< - zq skx ) dS k e 2 +Z JJ ( xq sky - yq- ) dS k e 3 ■ kS k kS k
В настоящей работе будем полагать, что моменты внутренних сил, вызванные действием напряжений %, % , равны нулю:
JJ ( у % - z % ) ds = 0, JJ x % = 0, JJ x сту ds = 0. S SS
В случае, когда поперечное сечение имеет вид такой же, как и на рис. 1, и нагрузки qj, q2, q3, q имеют вид qi = qe, q2 = q2e3, q = q3ei, q4 = q4ei и приложены к верхней и нижней граням стержня (см. рис. 14), соотношения примут вид
3 h i b i ( z )
Ri = Z J dz J %* + i=i hi-i - b ( z)
3 h i b i( z ) 3 h b i( z )
+ ZJ dz J %dVe.' +ZJ dz J %zidye3, i=1 hi-i — bi(z) i=i hi-i -bi(z)
R 2 = q dx ,
3 h i м z ) 3 h b i ( z )
Mi = Z J dz J z%xidye2 - Z J dz J y%•d’1'- i=i hi-i - b( z) i=i hi-i - bi( z)
M2 =
^ b(0) bn(hn)
J yq 2 dy + J yq i dy I e -
I-b(0) - bn (hn)
^ bn (hn) b(0)
-
- J xqdy + J xqdy I e2 +
-
V- bn (hn) - bi (0)
bn (hn) ( bn (hn) b(0)
+ h n J q 3 dy e 2 - J yq 3 dy + J yq 4 dy I e 3 +
-
- bn (hn) I-bn (hn) - b(0)
3 h i b i( z )
+Z Jdz J (yqskz - zqsky) dye - i=i hi- - b( z)
3 h b i ( z )
-
- Z J dz J ( xq skz - zq skx ) dy e 2 +
i =i h,-] - b ( z )
3 h i b i ( z )
+Z J dz J ( xq $ky - yq^k x ) dy e 3 ■ i =i h,-] - b ( z )
Выражения примут более простой вид, если положить, что вектор ускорения свободного падения g направлен вдоль осей OX или OZ . Тогда получим, что составляющая вектора массовой силы q ^ = 0. Если поперечные и продольные нагрузки симметричны относительно плоскости OXZ (функции qx , q 2, q 3, q4 являются четными функциями относительно переменной у ), тогда будут отсутствовать крутящие моменты и проекции изгибающих моментов на ось OZ внешних распределенных сил, т.е.
b i (0) b n ( h n )
J yq^dy = 0, J yqdy = 0,
- b i (0) - b n ( h n )
3 h i b i ( z )
Z J dz J ( yq skz - zq sky ) dy = 0, i = i h i - - b i ( z )
b n ( h n ) b (0)
J yq 3 dy = 0, J yq 4 dy = 0,
- b n ( h n ) - b i (0)
3 h i b i ( z )
Z J dz J ( x q sky - yq skx ) dy = 0 ,
*=i h i - - b i ( z )
и проекция главного вектора внешних сил на ось OY равна 0:
3 h i ЬЛ z )
Z J dz J q siy dy = °- i = i h i - 1 - b i ( z )
Также будут равны нулю проекции сил и моментов внутренних сил:
3 h i bi ( z ) 3 h i bi ( z )
Z J dz J % y-d y = 0 , Z J dz J y % xi dy = 0- i = 1 h i - 1 - b , . ( z ) i = 1 h,. - i - b i ( z )
В этом случае имеем задачу продольно-поперечного изгиба стержня.
Учитывая, что проекция главного вектора внутренних сил Rj на ось OX есть продольное усилие N, на ось OZ есть перерезывающая сила Qz, а проекция главного момента внутренних сил M на ось OY есть изгибающий момент M , получим
R = N + Qze3, M = Mye2, q = qxe + qzез, M, = Mye2, m = mye2, где
3 hi bi ( z ) 3 hi bi ( z )
N = E J dz J CT x dy , Q z = E J dz J CT zi dy , ‘= 1 h - 1 - b i ( z ) i = 1 h - 1 - M z )
3 hi bi ( z )
My = E J dz J z ct x dy , i = 1 h i — i - b i ( z )
b 1 (0) b n ( h n ) 3 h i b i ( z )
q x = J q з dy + J q 4 dy + E J dz J q sx dy ,
-
- W) — b n ( h n ) 1=1 h - - b i ( z )
b 1 (0) b n ( h n ) 3 h i b i ( z )
q z = J q 2 dy + J q , dy + E J dz J q sz dy ,
-
- b (0) - b n ( h n ) i =1 hM - b i ( z )
b n ( h n ) b 1 (0)
my = - J xqdy - J xqTdy +
-
- b n ( h n ) - b (0)
bn ( hn ) 3 hi bi ( z )
+ h n J q з dy - EJ dz J ( xq skz - zq skx ) dy •
-
- b n ( h n ) i =1 h - - b , (z )
Из условия равновесия отсеченной части dR
Rj + — 1 dx - Rj + R2 = 0 , R = q dx,
1 dx 1 22
d M d R
M + dx - M + (x + dx)e x (R + dx) - xe x R = 0, dxdx откуда, отбросив члены второго порядка получим:
dR
+ q = 0 , + e. x R = 0, dxdx dN dQdM
—+qx =0, +qz =0, -^m+my + Qz dx dxdx d2Mdm
-
-rr y -+- q z = 0-
- dx2
Положим, что закон изменения нагрузок сечения имеют вид малости,
= 0,
и форма
q1 t11 + t12X, q2 t21 + t22x, q3 t31 + t32 x, q4 t41 + t42X, b (z) = b01, b (z) = b02, b, (z) = b03
и сила тяжести направлена вдоль оси стержня, тогда получим:
q x = 2 b 01 ( 1 31 + 1 32 x ) + 2 b 03 ( 1 41 + 1 42 x ) + 2 g x E Pb 0i ( hi - h -1 ), =1
qz = 2b01 (t21 + t22x) + 2b03 (t11 + t12x)’ my = -2b03 (tux + tnx2) - 2b0j (t21x + t22x2) +
-
+ 2 b 03 h 3 ( t 31 + t 32 x ) + g x E P i b 0i ( h , 2 - h i - 1 )•
i = 1
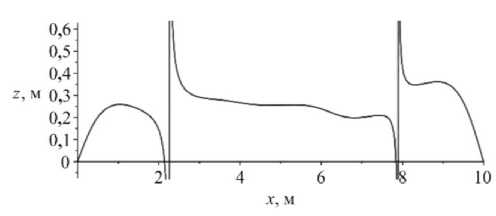
Координату z нейтральной линии можно определить из соотношения
£ 0 ( x ) + Z К y ( x ) = 0-
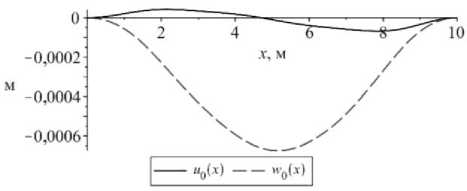
Результаты расчета стержня при N = 7, первый слой которого реализован из бетона марки B50, второй – B10, третий – B30, с параметрами boi = b03 = 0, 4 M, b02 = 0,3 M, h = “ M,
23 h = — M, h = — M, tn = 0, t12 = -6 кН/m3 , t21 = 0, t22 = 2 кН/м3, t31 = 0, t32 = -3 кН/м3, t41 = 0, t42 =-5,5 кН/м3,
P1 = P2 = P3 = 1800 кг/м3, приведены на рис. 15, 16.
б
Рис. 15. Изменение: а – величины перемещений; б – координаты нейтральной линии в сечении защемленного с обоих концов стержня
-
Fig. 15. The change of a ) the magnitude of displacements, b ) the coordinates of the neutral line in the cross section of the rod clamped at both ends
Как видно из рис. 16, а , деформация достигает предельного значения в середине стержня в третьем слое. Повысить несущую способность можно, заменив материал в третьем слое стержня на бетон марки B50 при тех же самых нагрузках. Решение, соответствующее данному случаю, изображено на рис. 17, 18.
Показанные примеры иллюстрируют, что на способность многослойных стержней из тяжелых бетонов выдерживать приложенные нагрузки значительно влияют способы закрепления стержней, форма поперечного сечения стержня, материал каждого слоя стержня.
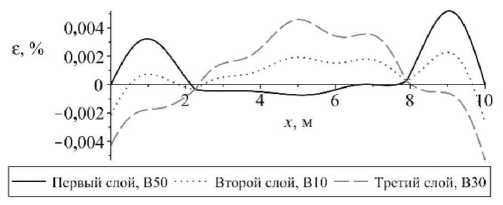
а
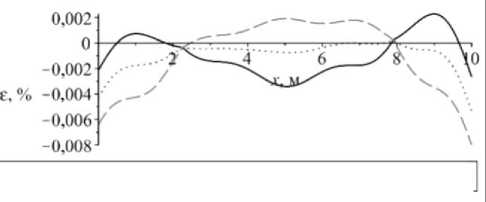
----Первый слой, В50...... Второй слой. В10--Третий слой. ВЗО
б
Рис. 16. Изменение величины: а – максимальной; б – минимальной деформации в сечении защемленного с обоих концов стержня
-
Fig. 16. The change in the value of a ) maximum, b ) minimum deformation in the cross section of the rod clamped at both ends
б
а
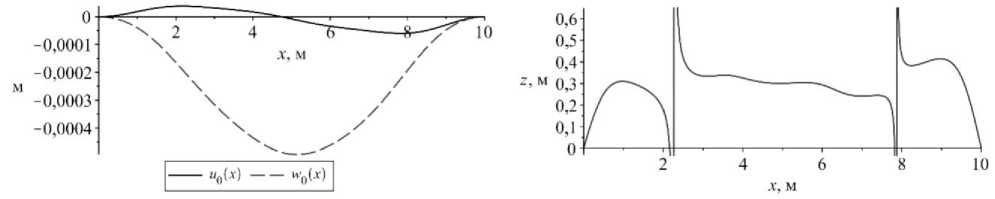
Рис. 17. Изменение: а – величины перемещений; б – координаты нейтральной линии в сечении защемленного с обоих концов стержня
-
Fig. 17. The change of a ) the magnitude of the displacements, b ) the coordinates of the neutral line in the cross section of the rod clamped at both ends

б
Рис. 18. Изменение величины: а – максимальной; б – минимальной деформации в сечении защемленного с обоих концов стержня
-
Fig. 18. The change in the value of a ) maximum, b ) minimum deformation in the cross section of the rod clamped at both ends
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-01-00038-а.
Список литературы Предельное состояние бетонных и железобетонных стержней при сложном и продольно-поперечном изгибе
- Мищенко А.В., Неимировский Ю.В. Нелинейное деформирование бетонных элементов при продольно-поперечном изгибе // Известия вузов. Строительство. – 2013. – № 4. – С. 5–12.
- de la Rosa Garsia P., Esminella A.C., Garsia M.N.C. Bending reinforcement of timber beams with composite carbon fiber and basalt fiber materials // Composite, Part B: Engineering. – 2013. – Vol. 55. – Р. 528–536.
- Немировский Ю.В. Метод расчета композитных стержневых систем из разномодульных материалов // Фунда-ментальные и прикладные проблемы современной механики: материалы V Всерос. науч. конф. – Томск, 2006. – С. 288–290.
- Гемлеринг А.В. Расчет стержневых систем. – М.: Строительство, 1974. – 208 с.
- Лукаш П.А. Основы нелинейной строительной механики. – М.: Строительство, 1974. – 208 с.
- Петров В.В. Нелинейная инкрементальная строительная механика. – М.: Инфра-Инженерия, 2014. – 480 с.
- Немировский Ю.В., Болтаев А.И. Диаграммы деформирования бетонов и железобетонов // Вестник Белгород-ского государственного технологического университета им. В.Г. Шухова. – 2015. – № 6. – С. 125–129.
- Немировский Ю.В., Батурин А.А. Метод расчета де-формативности и прочности однотавровых и двутавровых железобетонных стержней // Известия вузов. Строительство. – 2015. – № 10. – С. 82–93.
- Крусь Ю.А. Трансформирования диаграмм деформирования бетона при центральном сжатии и растяжении // Из-вестия вузов. Строительство. – 2008. – № 7. – С. 113–122.
- Адищев В.В., Демешкин А.Г., Роот В.В. Экспериментальное исследование процесса возникновения трещин нормального отрыва в изгибаемых армированных элемен-тах // Известия вузов. Строительство. – 2012. – № 3. – С. 121–126.
- Прогнозирование поведения железобетонных конструкций при сложных воздействиях природного и техноген-ного характера / В.О. Алмазов, А.В. Забегаев, Н.Н. Попов, С.В. Расторгуев [и др.] // Известия вузов. Строительство. – 1994. – № 11. – С. 10–15.
- Nemirovskii Y.V., Mishchenko A.V., Terletskii R.F. Dynamic analysis of composite rods under thermal and force loads // Journal of Mathematical Sciences. – 2017. – Vol. 223. – No. 1. – Р. 87–102.
- Немировский Ю.В. Допредельное деформирование гибридных армированных бетонных конструкций // Вестник Чувашского государственного педагогического университета им. И.Я. Яковлева. Серия: Механика предельного состояния. – 2018. – № 3(37). – C. 26–37.
- Маилян Л.Р., Иващенко Е.И. Расчет железобетонных элементов на основе действительных диаграмм деформирова-ния материалов. – Ростов н/Д: Изд-во Ростов. гос. строит. ун-та, 2006. – 222 c.
- Горшков А.Г., Трошин В.Н., Шалашилин В.И. Сопротивление материалов: учеб. пособие. – 2-е изд., испр. – М.: ФИЗМАТЛИТ, 2005. – 544 с.
- Иванов В.Н. Вариационные принципы и методы решения задач теории упругости: учеб. пособие. − М.: Изд-во РУДН, 2004. – 176 с.
- Голоскоков Д.П. Построение базиса для одномерных краевых задач в системах символьных вычислений // Про-странство, время и фундаментальные взаимодействия. – 2017. – Вып. 1. – С. 77–85.
- Самарский А.А., Гулин А.В. Численные методы. – М.: Наука, 1989. – 432 c.
- Пащанин А.А. Развитие методики расчета прочности железобетонных балок с использованием объемных конечных элементов: дис. … канд. техн. наук: 05.23.01. – М., 2011. – 179 с.
- Пащанин А.А. Расчет экспериментальных балок при действии поперечных сил с использованием объемных конеч-ных элементов // Бетон и железобетон. – 2011. – Вып. 6.
- Расчет прочности и трещиностойкости железобетон-ных элементов при совместном действии продольных сил, изгибающих и крутящих моментов / В.С. Плевков, И.В. Бал-дин, С.В. Балдин, Р.А. Плевков // Вестник Томского государ-ственного архитектурно-строительного университета. – 2018. – № 3. – С. 133–146.
- Балдин С.В. Прочность и трещиностойкость железо-бетонных элементов при совместном действии изгибающих моментов, продольных и поперечных сил от статического и кратковременного динамического нагружения: дис. … канд. техн. наук. – Томск, 2013. – 256 с.
- Иващенко Е.И. Разработка методов расчета железо-бетонных элементов на основе действительных диаграмм де-формирования материалов с учетом фактического изменения площади их поперечных сечений: дис. … канд. техн. наук. – Воронеж, 2006. – 230 с.
- Продольно-поперечный изгиб балки. Решение в различных программных комплексах / А.В. Савченко, А.В. Иос-кевич, Л.Ф. Хазиева, А.А. Нестеров, В.В. Иоскевич // Строи-тельство уникальных зданий и сооружений. – 2015. – № 11(38). – С. 89–105.
- Gorynin G.L., Nemirovskii Yu.V. Longitudinal–Trans-verse bending of layered beams in a three-dimensional formulation // Journal of Applied Mechanics and Technical Physics. – 2004. – No. 45(6). – P. 885–893.
- Плевков В.С., Колупаева С.Н., Кудяков К.Л. Расчетные диаграммы нелинейного деформирования базальто-фибробетона при статических и кратковременных динамических воздействиях // Вестник Томского государственного архитектурно-строи-тельного университета. – 2016. – № 3. – С. 95–110.
- Горохов М.С. Математическая модель проектирования железобетонного корпуса стоечного судна в задаче обоснования его системы набора // Вестник Волжской государственной академии водного транспорта. – 2016. – № 46. – С. 63–71.
- Influence of continuous plastic fibers reinforcement ar-rangement in concrete strengthened / F.J. Baldenebro-Lopez [et al.] // IOSR Journal of Engineering. – 2014. – Vol. 04, iss. 04. – P. 15–23.
- Thorhallsson E.R., Snaebjornsson J.T. Basalt Fibers as New Material for Reinforcement and Confinement of Concrete // Solid State Phenomena. – 2016. – Vol. 249. – P. 79–84.


