Предельные биполярные последовательности для робастного маркирования цифровых аудиосигналов по методу лоскута

1. Введение. Широкое распространение и использование цифрового аудиоконтента остро ставит вопрос о необходимости его стеганографической защиты для доказательства авторского права, права собственности, возможности отслеживания сделок и оплаченной рекламы, контроля целостности и решения других задач [1, 2]. Это, в свою очередь, требует развития робастных методов цифрового маркирования и построения аудиостегосистем, устойчивых к атакам, действию помех и преобразованиям. Целью возможных атак может быть удаление, разрушение или нелегитимное извлечение внедренного цифрового маркера (цифрового водяного знака).

Существует достаточно большое количество робастных методов маркирования цифровых аудиосигналов, связанных с погружением цифровых водяных знаков или скрытием передаваемой аудиоинформации [1, 2]. Одним из наиболее используемых и достаточно устойчивых является метод лоскута (от англ. patchwork). Этот метод представляет собой статистический метод маркирования цифровых объектов [3, 4, 5]. Принцип маркирования методом лоскута состоит в следующем. В цифровом объекте в соответствии со стегоключом случайным образом выбирается пара одинаково распределенных элементов. Затем амплитуда одного элемента из каждой пары увеличивается на определенную величину, тогда как амплитуда другого элемента этой пары уменьшается на такую же величину. Путем такой модификации амплитуд можно закодировать, например, один бит внедряемого цифрового маркера (цифрового водяного знака). Этот процесс случайного выбора пар с последующим изменением амплитуд элементов повторяется достаточное количество раз для того, чтобы обеспечивалась статистическая устойчивость внедренного маркера к помехам и предполагаемым атакам на маркированный цифровой объект. Реализация метода лоскута основана на применении биполярных последовательностей.

Метод лоскута и принципы, лежащие в его основе, широко используются для маркирования цифровых аудиосигналов (речь и музыка), цифровых изображений и видео, а также в кодах компьютерных программ [6 – 16]. При этом робастность маркирования методом лоскута обеспечивается применением специальных биполярных последовательностей при формировании и внедрении маркера в покрывающий объект – цифровой аудиосигнал, и корреляционного детектирования при обнаружении и извлечении маркера (выделении информационных битов маркерной последовательности).

В последние годы получило широкое развитие маркирование цифровых аудиосигналов методом лоскута с использованием специальных расширяющих биполярных последовательностей для решения задач, связанных с использованием цифровых водяных

_______DIGITAL INFO_RMATIO_N TELECO_MM_UNICATION TEC_HNO_LOGIES_______ знаков, скрытием передаваемой аудиоинформации, позиционированием маркированными аудиосигналами нелегитимного приемного устройства. В статьях [17 – 21] изложен традиционный подход к маркированию цифровых аудиосигналов по методу лоскута в частотной области Фурье, когда маркированный аудиосигнал предполагается передавать через воздушный аудиоканал или радиоканал. В этом случае маркер формируется из псевдослучайной биполярной числовой последовательности с почти равновероятным распределением элементов (1 и -1 ) и из расширяющей ее последовательности определенного вида. При этом корреляционные свойства расширенной маркерной последовательности практически не зависят от соответствующих свойств исходной последовательности, а определяются корреляционными свойствами расширяющей    биполярной последовательности (РБП). Одно из свойств автокорреляционной функции (АКФ) расширяющей биполярной последовательности – абсолютное значение величины отношения максимума АКФ к её минимуму при этих условиях с высокой точностью приближается к 2. Это позволяет использовать данное свойство как критерий при выборе специальных РБП и построении на их основе специальных маркерных последовательностей с улучшенными корреляционными свойствами, повышающими качество детектирования и устойчивость маркирования цифровых аудиосигналов.

Другие особенности и свойства АКФ расширенной маркерной последовательности накладывают ограничения на выбор расширяющей последовательности при решении задачи позиционирования маркированными аудиосигналами приемного устройства. В работах [21, 22] показано, что для этой задачи наилучшая длина расширяющей последовательности равна двум разрядам. Увеличение длины расширяющей последовательности негативно сказывается на точности определения местоположения нелегитимного приемника с помощью приема и передачи маркированных аудиосигналов.

В статьях [23, 24] предлагается метод маркирования аудиосигналов с использованием выбранных из эвристических соображений расширяющих биполярных последовательностей с улучшенными корреляционными свойствами, повышающими качество детектирования, которым свойственно большее, чем два, по абсолютному значению отношение максимума ее АКФ к минимуму этой функции. Повышение качества детектирования происходит вследствие того, что увеличение абсолютного значения этой величины

_{_}ЦИ_{_}ФРОВЫЕ ИН_{_}ФОР_{_}МАЦ_{_}ИОН_{_}НО-ТЕЛЕКОМ_{_}МУНИКАЦИ_{_}ОНН_{_}ЫЕ ТЕХНОЛО_{_}ГИИ_{_} обычно приводит к увеличению устойчивости к атакам, и, в частности, к атаке аддитивным белым гауссовским шумом при использовании корреляционного детектора.

В связи с этим представляется актуальной задача разработки математического аппарата построения таких специальных биполярных последовательностей с улучшенными корреляционными свойствами, у которых по абсолютному значению отношение максимума автокорреляционной функции к её минимуму будет максимально возможным.

Целью данной работы является разработка методов поиска и построения нового класса последовательностей – предельных расширяющих биполярных последовательностей, у которых автокорреляционные функции обладают максимально возможными по абсолютному значению отношениями максимума к минимуму, и применение которых повышает устойчивость цифрового маркирования.

Для достижения этой цели:

• -    Исследованы особенности АКФ расширяющих биполярных последовательностей и сформированных на их основе маркерных последовательностей, используемых при традиционном маркировании цифровых аудиосигналов. Предложены специальные функции для построения РБП с улучшенными корреляционными свойствами для робастного маркирования и предельных биполярных последовательностей, АКФ которых обладают максимально возможными по абсолютному значению отношениями максимума к минимуму. Сформулированы и доказаны теоремы и следствия из них о существовании верхней границы минимальных значений автокорреляционных функций таких последовательностей и о значениях первого и второго лепестков АКФ. На этой основе дано строгое математическое определение предельных биполярных последовательностей.

• -    Разработаны два метода поиска и построения предельных биполярных последовательностей: с использованием рационального перебора и на основе введенных порождающих функций, функционально связанных с такими последовательностями.

• -    Проведено компьютерное моделирование по оценке значений абсолютной величины отношения максимума к минимуму автокорреляционной и взаимной корреляционных функций исследуемых биполярных последовательностей для наихудших условий извлечения маркерных последовательностей (слепой прием).

• 2.    Традиционное маркирование с использованием расширяющих биполярных последовательностей. Традиционно маркер формируется из псевдослучайной биполярной числовой последовательности:

В этом случае искажающим воздействием (шумом) становился сам покрывающий цифровой аудиосигнал.

Теоретический вклад настоящей работы в решение задачи робастного маркирования цифровых аудиосигналов по методу лоскута заключается в разработке математического аппарата для построения предельных расширяющих биполярных последовательностей с улучшенными корреляционными свойствами, более устойчивых к действию помех и искажающих воздействий при обнаружении и извлечении цифровой маркерной последовательности.

a = ( а 1 , a ₂,..., U n _a ) , a e { 1, - 1 } ,

где N _α – длина последовательности. После формирования последовательности α её элементы расширяются путем подстановки вместо них последовательности следующего вида:

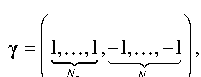
γ

где N _П – положительное целое число, определяющее половину длины расширяющей последовательности.

Затем формируется маркерная последовательность:

m = ( №i, m 2,..., m 2 n п na ) = a 0 Y, где 0 - оператор кронекерова произведения,

I i ^{- 1} I

/   - \ |--- | mod 2

m_t = ( - 1 ) L ^N п J a

где L x J — ближайшее целое, меньшее или равное числу x .

Прежде чем, перейти к анализу корреляционных свойств маркерной последовательности, определим АКФ произвольной вещественной последовательности:

Р = ( Pi, P 2 , — , P l ) ,                              (5)

как дискретную функцию от целочисленной переменной k , удовлетворяющую следующему равенству:

L fАКФ (Р, k ) = £PiPi-k ,                           (6)

i =1

где числа p_l являются элементами вещественной последовательности p , когда индекс l e { 1,2, — , L } , но для сокращения обозначений будем считать P_l = 0, когда индекс l ^ { 1,2, — , L } .

Использование расширяющих последовательностей γ вида, описываемого равенством (2), приводит к тому, что у АКФ сформированной маркерной последовательности m в соответствии с (3) появляются большие по амплитуде отрицательные значения. Это уменьшает абсолютное значение отношения максимума АКФ к её минимуму по сравнению с таким же значением АКФ для биполярной последовательности α . При этом абсолютное значение этого отношения оказывается приблизительно равным два в тех случаях, когда исходная псевдослучайная последовательность α генерируется таким образом, что вероятности появления 1 и - 1 оказываются почти равными.

Это свойство АКФ биполярной последовательности, используемой при традиционном маркировании, можно обосновать с помощью следующих рассуждений. Когда в псевдослучайных биполярных последовательностях а вероятности появления 1 и - 1 приблизительно одинаковые, тогда можно получить оценку максимального падения АКФ маркерной последовательности m , опираясь на среднее значение АКФ маркерной последовательности m , вычисленное для единичного сдвига от центрального значения АКФ маркерной последовательности m . Действительно, значение АКФ маркерной последовательности m , получаемое при единичном сдвиге маркерной последовательности m относительно центрального значения АКФ, включает в себя все подстановочные (расширяющие)

последовательности ( 1, - 1 ) , значит, падение значения АКФ окажется максимальным. Среднее значение на отдельную подстановку (в зависимости от результатов соседних подстановок) можно вычислить, исходя из значений для каждого из возможных вариантов, составляющих значения АКФ. С учетом симметрии АКФ возможны два варианта составляющих значения, как показано на рисунке 1. Без учета - четыре варианта составляющих, два из которых будут давать такой же вклад в значение АКФ, какой дают элементы другой пары составляющих.

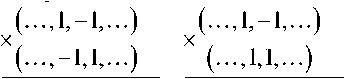
вклад в значение АКФ равен О

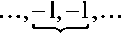
вклад в значение АКФ равен -2

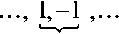
Рис. 1. Составляющие значения АКФ

Так как таких составляющих будет в среднем одинаковое количество, то, исходя из них, среднее арифметическое значение оказывается равным единице со знаком минус, что указывает на падение центрального значения АКФ в 2 раза. То есть, если центральное значение АКФ псевдослучайной последовательности после подстановки расширяющей последовательности ( 1, - 1 ) , равно X, то минимальное значение в среднем будет равно - X /2.

Например, последовательность Баркера длиной 7:

^а = ( ^{1,1,1, - 1, - 1,1, - 1} ) ,                               (7)

после подстановки последовательности y = ( 1, — 1 ) , станет маркерной последовательностью:

m = ( 1, - 1,1, - 1,1, - 1, - 1,1, - 1,1,1, - 1, - 1,1 ) ,                    (8)

у которой максимум АКФ равен 14, а минимум -7 и, следовательно, по абсолютной величине их отношение равно |14/ ( - 7 )| = 2 .

Исходя из этих рассуждений и результатов проведенного моделирования, можно сделать следующие выводы относительно особенностей и свойств АКФ маркерной (расширенной) последовательности, сформированной в соответствии с равенствами (1)– (3). При традиционном маркировании значение этой АКФ оказывается минимальным на «расстоянии» одного сдвига относительно центрального значения, что связано с длиной расширяющей последовательности ( 1, - 1 ) . Максимальное значение АКФ маркерной последовательности m зависит от длины расширяемой псевдослучайной последовательности α и от длины расширяющей последовательности ( 1, - 1 ) . Тогда как минимальное значение АКФ маркерной последовательности m тем ближе по абсолютному значению к половине центрального значения, чем больше длина псевдослучайной последовательности α и чем более равновероятным является появление 1 и - 1 в ней. При выполнении последнего условия, когда в качестве расширяемой последовательности α используется псевдослучайная биполярная последовательность, у которой вероятности появления 1 и - 1 почти равны, АКФ расширенной последовательности m будет определяться корреляционными свойствами расширяющей последовательности γ , а не корреляционными свойствами расширяемой последовательности α . И еще одно важнейшее свойство АКФ – абсолютное значение величины отношения максимума АКФ к её минимуму с высокой точностью приближается к 2. Это позволяет сформулировать критерии для поиска расширяющих биполярных последовательностей γ , обладающих улучшенными корреляционными свойствами и большей устойчивостью.

С учетом выявленных выше свойств АКФ расширенной биполярной последовательности и в развитие статей [23, 24] далее предлагается метод построения специальных расширяющих биполярных последовательностей для робастного маркирования, позволяющий обеспечить большее, чем 2 по абсолютному значению отношение максимума АКФ маркерной последовательности m к минимуму этой функции.

• 3.    Предельные биполярные последовательности для робастного маркирования. Если вместо традиционной расширяющей последовательности у = ( 1, - 1 ) в равенстве (3) использовать расширяющую последовательность вида:

Y = Ф ® Y трад , (9)

где:

• ^Y трад - ( 1, ^{- 1 )} .

  
  

При этом, когда для формирования γ применяется специально выбираемая биполярная последовательность:

ф ^- ( ф_р Ф 2 , _ , фу ф ) , ф е { 1, — 1 } ,                       (11)

то можно обеспечить превышающее 2 значение абсолютной величины отношения максимума АКФ к её минимуму у маркерной последовательности m .

Использование биполярной последовательности γ вида (9), вместо биполярной последовательности вида (2), приводит к тому, что маркерная последовательность m уже не будет определяться уравнением (3), а будет с учетом (1) удовлетворять следующему равенству:

где:

m ^- ( т,,m 2 , _ ,m 2 N ф N а ) ^{- а} 0 Y ,

mi

. ( i -1 ) mod 2

Фг а .

’                         ^r ( I -11       . .. 1 . I .-1 I

— mod Nm +1  2_L Li ф            +

W                  ^ X N ф J

Например, если:

ф - (-1,-1,1,-1), то получится расширяющая последовательность:

Y ^- (^{- 1,1, - 1,1,1,} - 1, ^{- 1,1} ) ,

у которой максимум АКФ равен 8, а минимум - 3, то есть, в этом случае у последовательности γ значение абсолютной величины отношения максимума АКФ к её минимуму равно 1- 8 / 3| - 2.667 .

Выполнив подстановку этой последовательности у вместо элементов последовательности Баркера длины 7:

^а - ( 1,1,1, — 1, — 1,1, — 1 ) ,                               (16)

будет получена биполярная последовательность длиной 56:

m = ( - 1,1, - 1,1,1, - 1, - 1,1, - 1,1, — 1,¹,¹, - 1, - 1,1, ^- 1,1, - 1,1,1, - 1, - 1,1,1, - 1,1, - 1, - 1,1,1, - 1, 1, - 1,1, ^- 1, — 1,1,1, ^- 1, ^{- 1,1,} — 1,1,1, ^{- 1, - 1,} l-,^{1, -} 1,1, - 1, — ид, ^{- 1} ) ,

у которой максимум АКФ равен 56, а минимум - 21 (рисунок 2). Следовательно, у последовательности m абсолютное значение отношения максимума АКФ к минимуму этой функции равно |- 56/21| - 2.667 , что больше на 33%, чем в случае, если бы вместо последовательности (15) использовалась последовательность у трад , применяемая в традиционном маркировании (рисунок 3). Напомним, что при традиционном подходе значение этого отношения с высокой точностью приближается к 2. 60

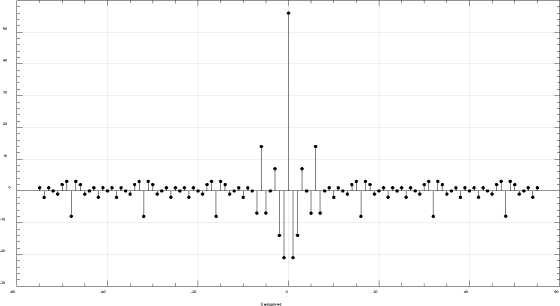
Рис. 2. График автокорреляционной функции маркерной последовательности (17), основанной на специальной расширяющей последовательности Y - ( 1, - 1, - 1,1,1, - 1, - 1,1 ) .

-5

-10

-20

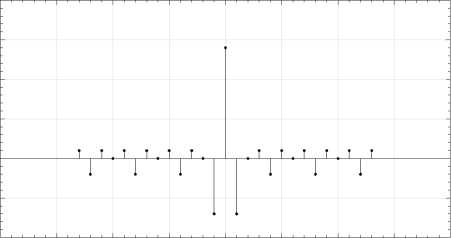
Рис. 3. График автокорреляционной функции маркерной последовательности (8), основанной на традиционной расширяющей последовательности

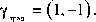
Таким образом, с учетом того, что расширяющая последовательность γ в основном определяет автокорреляционные свойства расширенной последовательности m , когда биполярная последовательность α является псевдослучайной, то требуется метод получения таких последовательности γ , у которых автокорреляционные функции имеют наибольшие минимумы среди минимумов автокорреляционных функций всех прочих удовлетворяющих равенству (9) биполярных последовательностей такой же длины.

По определению значение АКФ f _AK. ( у , k ) последовательности у , описываемой формулой (9), когда смещение k принадлежит множеству:

{-2Nф + 1,-2Nф + 2, —,-1,0,1,2,^,2Nф - 1},(18)

удовлетворяет следующему равенству:

fАК.(у,к)=2£'k(-Гя-чиНУ1k| ■■

=1                  [ 2 J[

² N Ф-I k       Ф ш Ф

£ ( — 1 ) ² -+| k ^{- 2}

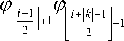
i =1

где |х| - абсолютное значение числа x, а ^x J - ближайшее целое, меньшее или равное числу x .

Полезно эту АКФ представить в следующем виде:

2 zk. , если k mod 2 = 0,

^f АКФ ( Y , ^k M- z k -1 ^- z | k -2| , если ^k mod ² =1 и ^k * ^{2 N} Ф - ¹

2        [ 2 J ⁺ 1

- z_k -1 , если k = 2 N ф - 1, 2

где:

N ф - j zj = z -j = E ^i^i+j, j е{0,1,., NP - 1}-                 (21)

i =1

При этом, учитывая, что ^ i е { 1, - 1 } , будет выполняться следующее равенство:

z 0 = N ф .                                  (22)

Так как конкретные значения z j и z - j (при j е { 1,2,..., N _ф - 1 } ) будут определяться элементами последовательности φ , использованной при формировании последовательности γ , то для z_j и z - j , когда j е { 1,2, . , N _ф - 1 } , можно указать лишь множества потенциальных значений:

zj,z-je{±( a + j-1), ±( a + j + 1), ±( a + j + 3), •••’ ±( Nф -j)},     (23)

где:

a = ( N _ф - 1 ) mod2.

Следовательно, количество различных автокорреляционных функций, соответствующих одному и тому же Nφ , меньше количества последовательностей γ . Поэтому всё множество последовательностей γ , соответствующих одному и тому же Nφ , можно поделить на непересекающиеся подмножества, в которые попадут последовательности, имеющие одинаковые автокорреляционные функции.

Теорема 1 (О существовании верхней границы для минимального значения АКФ биполярной последовательности у ). Среди всех биполярных последовательностей φ , определенных равенством (11) и имеющих одинаковую длину N _φ , нет такой, которая позволяет получить в соответствии с правилом (9) биполярную последовательность γ , у которой АКФ имеет минимум, который больше величины:

N φ

—

—

N φ ,

то есть для всех таких биполярных последовательностей γ одинаковой длины справедливо неравенство:

m i nfA™ ( Y , k ) ^

N φ

—

— N ф .

Доказательство. Так как для N _ф = 1 условие этой теоремы выполняется, поэтому ниже предлагается доказательство для N _ф >  1.

Предположим обратное – а именно, что среди биполярных последовательностей φ , определяемых равенством (11), существует такая последовательность, обозначим ее φ ˆ , из которой в соответствии с правилом (9) получается биполярная последовательность γ ˆ , у которой АКФ имеет минимальное значение, которое больше величины (25). В таком случае автокорреляционная функция f _АКФ ( Y , к ) (19), (20) последовательности у, имея максимум, равный

2 z ₀ = 2 N _ф , имеет минимум, который больше ¹ :

N ф - 1

-

N φ .

Значит, для этой АКФ обязательно выполняются следующие два неравенства:

f

АКФ

^— z 0

—

z 1 >

N φ

—

—

N φ ,

f

АКФ

(Y,2) = 2 z1 >

N φ

—

—

N φ .

Исходя из того, что z0 = Nф, неравенство (28) позволяет заключить, что z1 должно удовлетворять следующему неравенству:

zi < —

N , — 1

Тогда как на основании неравенства (29) получается, что:

z ₁

N ф — 1

> ----

—

N φ

Следовательно, величина z ₁ должна принадлежать диапазону:

N ф — 1

—

N φ

< Z1 < —

N ф — 1

Нетрудно показать, что расстояние между правой и левой границами этого диапазона удовлетворяет равенству:

—

N ф — 1

N ф — 1

—

N φ

1 + 3

J Nф — 11 1 3

где { a } - это дробная часть вещественного числа a . Так как в данном случае выполняется равенство:

N

—

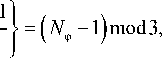
то,

1 + 3

J Nф —1I 1 3

Таким образом, возможны три ситуации:

1 + 3

N φ

—

1/2, если N ф е { 1,4,7, ™ } , 1,если N ф е { 2,5,8, ™ } , 3/2,если N ф е { 3,6,9, ™ } .

В первом и во втором случае, когда расстояние между границами неравенства (32) равно 1 2 и 1, соответственно, не существует подходящих целочисленных значений z1 . Однако, в третьем случае, расстояние между границами неравенства (32) становится наибольшим и оказывается равным 32. Например, когда

N = 9 , тогда —< z. <— 2, или, когда N = 12, тогда —< z <— 3.

φ                       2 1                               φ                       2 1

Можно предположить, что, когда Nф е{3,6,9,™}, подходящим значением для z1 является:

N ф - 1

N φ

где Р а "| - ближайшее целое, большее или равное вещественному числу a . Но, в тех случаях, когда число N _φ четно, тогда и величина (36) является четной, однако, в таком случае z ₁ не может принимать четные значения (23). И наоборот, когда величина (36) нечетная, тогда и число N _φ также является нечетным, но в таком случае z ₁ не может принимать нечетные значения. Следовательно, во всех этих случаях z ₁ не может принять значение равное величине (36).

Таким образом, среди биполярных последовательностей φ , определяемых равенством (11), нет такой последовательности φ ˆ , из которой в соответствии с правилом (9) получается биполярная последовательность γ ˆ , у которой АКФ имеет минимум, больше величины (25).

Следствие из Теоремы 1 (О предельной величине верхней границы отношения по абсолютному значению максимума АКФ биполярной последовательности γ к минимуму этой функции). В пределе с увеличением длины N _φ последовательности φ , абсолютное значение отношения максимума к минимуму АКФ последовательности γ равно 3.

Действительно, проведя преобразования, получим:

lim

N , — 1

= lim

N ф ^“

6 N φ

= 3,

- 2 N - 1 - 3 ^φ

где { а } - это дробная часть числа a .

Определение. Предельной биполярной последовательностью γ, удовлетворяющей равенству (9), называется такая (обозначим ее Y„), У которой АКФ имеет минимальное численное значение, равное величине (25):

m ^ k n ^С АКФ ( Y „ , k ) =

N ф - 1

-

N φ .

Исходя из равенства (38) можно заключить, что у предельных последовательностей у „ автокорреляционные функции такие, что для всех k из множества (18) выполняются неравенства:

^f АКФ ( Y „ , k ) ^

N φ

—

— N ф ,

которые, с учетом равенства к следующим (когда Nф > 1):

(20) и z ₀ = N _ф , можно свести

N ф — 1

—

j —1 ^,

где j е { 1, _ , N ф ^— 1 } .

Автокорреляционные функции всех предельных биполярных последовательностей у „ обладают общим свойством, доказательство которого приведено далее в Теореме 2.

Теорема 2 (о значениях первого и второго лепестков АКФ предельной биполярной последовательности) . АКФ предельной последовательности у „ является такой, что для неё выполняется либо равенство:

С акф ^{( Y} » ,1 )

N ф — 1

N φ ,

либо равенство:

^f АКФ ^{( Y} » ,

N ф - 1

N φ ,

но не оба сразу.

Доказательство. Так как для N _ф = 1 условие этой теоремы выполняется, поэтому ниже предлагается доказательство для N _ф >  1.

Предположим обратное, что для любой предельной последовательности у„ при выполнении:

minfA™ ( 7 » , ^к ) =

N ф — 1

N φ ,

для всех к е { 3,4, ^ ,2 N _ф - 1 } выполняется неравенство:

^f АКФ ( Y „ , ^к ) ^

N ф — 1

- N ф ,

но для всех к е { 1,2 } выполняется либо неравенство:

^f АКФ ( Y „ , ^к ) >

N _Р — 1

N φ ,

либо равенство:

^f АКФ ( Y „ , ^к ) =

N ф — 1

N φ .

Если для всех к е { 1,2 } выполняется неравенство (45), то в таком случае z ₁ должно удовлетворять двойному неравенству (32), для которого при доказательстве Теоремы 1 было показано, что не существует такого z ₁ , который удовлетворял бы ему.

Теперь, если будет опровергнуто равенство:

fакф (Y„,1) = fАКФ (Y» ,2),(47)

то теорема будет доказана. Предположим обратное, что равенство (47) выполняется, тогда выполняется и равенство:

-z0 - Z1 = 2zr

В таком случае, с учетом равенства z ₀ = N _ф , будет:

N z i =- -Л.(49)

Так как z ₁ является целым числом, то это равенство не может выполняться для значений N _φ не кратных 3. Тогда, рассмотрим только такие значения N _φ , которые кратны 3 – в таких случаях отношение справа от знака равенства (49) будет целым числом. Во-первых, это отношение будет равно нечетному числу, когда N _φ равно нечетному числу, кратному 3. Во-вторых, это отношение будет равно четному числу, когда N _φ равно четному числу, кратному 3. Но при нечетном N _φ число z ₁ может быть только четным (23), и, наоборот, – при четном N _φ число z ₁ может быть только нечетным. Значит, равенство f _AKO ( y „ ,1 ) = f _AK® ( Y » ,2 ) также не выполняется.

Следствие из Теоремы 2. У предельных последовательностей Y „ , когда N _ф >  1, автокорреляционные функции такие, что:

z i =1

N ф — ¹

- 1, если ( N _ф + 1 ) mod3 = 0,

N φ

иначе.

Доказательство.

Когда для АКФ предельной

последовательности y „ выполняется равенство:

f

АКФ

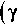
да ,

N φ

—

—

N φ ,

тогда:

^— z 0 ^— z 1 -

N ф — 1

—

N φ .

В таком случае, с учетом равенства z0 - Nф, будет выполняться равенство:

zi - —

N ф — 1

Однако это равенство, учитывая свойство (23), может выполняться только, когда четность числа Nф — 1 совпадает с четностью числа

N _v — 1

то есть равенство (53) выполняется только для тех чисел

N _φ , для которых выполняется равенство:

( ^N ф ^— 1 ) mod^{2 -}

N ф — 1

mod 2.

Таковыми являются числа   Nф е{1,3,4,6,7,9,10,12,13,...}. Этим доказана нижняя половина кусочно-определенного равенства (50).

Теперь докажем верхнюю половину (50). Когда для АКФ предельной последовательности у „ выполняется равенство:

^f АКФ ^{( Y} да ,2 ) ^-

N ф — 1

—

N φ ,

тогда:

z ₁

N ф - 1

— Nф

.

С одной стороны, правая часть равенства (56) принимает целые значения, только когда N _ф е { 2,5,8,11,14,17,20,... } , то есть когда:

( N _ф + 1 ) mod3 = 0.

С другой стороны, учитывая свойство (23), равенство (56) может выполняться, только когда четность числа N _ф - 1 совпадает с четностью правой части равенства (56) числа, то есть для таких положительных целых чисел N _φ , для которых выполняется равенство:

( N ф ^— 1 ) ^mod2 =

N ф — 1

—

N φ

mod 2.

Но это равенство как раз и выполняется, когда N _φ удовлетворяет равенству (57). При этом, когда N _φ удовлетворяет равенству (57), тогда выполняется равенство:

N φ

— 1

—

N φ

N , — 1

— 1.

Действительно, если вычесть из левой части этого равенства правую, то получается следующее равенство:

N φ

— 1

—

N φ

N ф — 1

1 — 3

N φ

—

где { a } - это дробная часть числа а . Но,

N ф — 1

= 1,

когда N _φ удовлетворяет равенству (57). Значит, когда N _φ удовлетворяет равенству (57), будет выполняться равенство:

1 - 3

N , — 1

= 0.

Следовательно, когда N _φ удовлетворяет равенству (57), тогда выполняется равенство (59). Тем самым доказана верхняя половина кусочно-определенного равенства (50).

Следует отметить, что с формальной точки зрения, величина z ₁ не определена, когда N _ф = 1 (21). Но если принять, что z 1 = 0 , когда N _ф = 1, то (50) будет выполняться и для случая N _ф = 1.

• 4.    Метод поиска полного множества предельных последовательностей на основе рационального выбора. Равенство (50) с учетом равенства (21) можно представить в следующем виде:

  N , -1

  2>- =]

  =1

  
  

  ^N , - ¹

  
  

  - 1, если ( N _ф + 1 ) mod3 = 0,

  
  

  _-

  
  

  N φ

  
  

  _-

  
  
  
  
  
  
  
  

  ^,

  
  

  иначе.

  
  

Поэтому, опираясь на Следствие из Теоремы 2, можно сказать, что при поиске предельных последовательностей у „ можно ограничиться только множеством Φ из таких биполярных последовательностей φ длиной N _φ , для которых выполняется кусочно-определенное равенство (63).

С учетом равенства (21) числа z _j можно определить как сумму элементов последовательности следующего вида:

^v j = ( v\,_P v 2. , , - , vv ф - j , j ) ,                            ⁽⁶⁴⁾

где:

v_l,i= V i V i + j .                                       (65)

Так как v i e { 1, - 1 } , то v i j e { 1, - 1 } .

Важно отметить, что элементы последовательности v _j , когда j >  2, можно вычислить по элементам двух предыдущих последовательностей v j 1 и v j _{- 2} следующим образом:

v , j = V , j -1 V +1, j -2 V +1, j -1 .

Действительно, произведение справа от знака этого равенства совпадает с правой частью равенства (65):

= V i V i + j - 1 V i + 1 V i + j = V i V i + j .

^V _v-1 v i -+1, _y -2 v i -+1, _y -1 = V i V i + j - 1 V i + 1 V i + 1 + j - 2 V i + 1 V i + 1 + j - 1

Любой вектор v ₁ связан с двумя биполярными последовательностями φ . При этом эти две последовательности определяют две последовательности γ , у которых совпадают автокорреляционные функции. Так, когда известен вектор v ₁ , тогда восстановить элементы упомянутых двух биполярных последовательностей φ , с которыми он связан, можно по следующему правилу:

• 1)    Прямая последовательность ф : пусть v 1 = - 1, тогда:

i -1

V =- n V / ,1 , i e { 2,3, ^ ,N ф } .                     (67)

l =1

• 2)    Инвертированная прямая последовательность φ : пусть

• V 1 = 1, тогда:

  -1

V i = n V i ,1 , i e { 2,3, ^ ,N ф } .                         (68)

i =1

Таким образом, множество Φ соответствует множеству V ₁ из таких последовательностей v ₁ , у которых сумма элементов равна числу z 1 , удовлетворяющему равенству (50). А так как v i j е { 1, - 1 } , то мощность множества V ₁ равна биномиальному коэффициенту:

N ф ^{- 1 +} z 1

I Vil = C где:

ⁿ ф ^{- i +} z i

C N _φ

- 1

( ^N ф - 1 ) !

.

( N -1 + гЛ NN -1 - гЛ

φ 1 ! φ 1 !

I 2 Л 2 У

Если некоторая последовательность v1 е V1 связана с последовательностью φ , которая в свою очередь определяет предельную последовательность у„ , тогда сумма элементов каждой из последовательностей множества   {v1, v 2,..., vN

1 } удовлетворяет

- 1

двойному неравенству (40).

А теперь, для примера выполним поиск всех предельных последовательностей у „ для N _ф = 4 • Поиск представлен в виде следующей последовательности действий:

• 1)    Так как N _ф = 4, то, в соответствии с равенством (50), выполняется следующее равенство: z 1 = - 1.

• 2)    Так как N _ф = 4 и z 1 = - 1, то поиск подходящих последовательностей v 1 длиной N _ф - 1 = 3 , следует вести среди всех таких биполярных последовательностей, у которых сумма элементов равна - 1.

• 3)    В соответствии с равенством (69), множество V ₁ проверяемых последовательностей v 1 , длиной N _ф - 1 = 3 , имеет мощность |V 1| = 3.

С учетом того, что в это множество должны войти все последовательности v 1 длиной 3, у которых сумма элементов равна - 1, то оно будет следующим:

V = { ( - 1, - 1,1 ) , ( - 1,1, - 1 ) , ( 1, - 1, - 1 ) } .

• 4)    Определим по формуле (66) для каждой из этих трех последовательностей последующие за ними последовательности v ₂ и v ₃ : для последовательности v 1 = ( - 1, - 1,1 ) , это будут: v ₂ = ( 1, - 1 ) и v ₃ = 1; для последовательности v 1 = ( - 1,1, - 1 ) : v ₂ = ( - 1, - 1 ) и v ₃ = 1; для последовательности v 1 = ( 1, - 1, - 1 ) , последующими будут: v ₂ = ( - 1,1 ) и v ₃ = 1.

• 5)    Так как сумма элементов последовательности v j равна величине z j , то можно проверить, определяет ли какая-то из последовательности множества V ₁ предельную последовательность Y „ . Учитывая, что z 1 = - 1 и, что у предельных последовательностей Y „ выполняются двойные неравенства (40). Следует проверить выполняются ли два двойных неравенства:

3              3

— < z, < 4, — < z3 < 3 - z..

2      ²           2      ^{3         2}

• -    Выполним проверку для вектора v 1 = ( - 1, - 1,1 ) .

Суммы элементов векторов v ₂ и v ₃ равны z ₂ = 0 и z ₃ = 1, соответственно. Оба двойных неравенства удовлетворяются. Следовательно, вектор v 1 = ( - 1, - 1,1 ) успешно проходит проверку, так как определяет предельные последовательности у „ .

• -    Выполним проверку для вектора v 1 = ( - 1,1, - 1 ) .

Суммы элементов векторов v ₂ и v ₃ равны z ₂ = - 2 и z ₃ = 1, соответственно. Первое двойное неравенство не удовлетворяются. Следовательно, вектор v 1 = ( - 1,1, - 1 ) не проходит проверку, так как не определяет предельные последовательности у „ •

• -    Выполним проверку для вектора v 1 = ( 1, - 1, - 1 ) .

Суммы элементов векторов v ₂ и v ₃ равны z ₂ = 0 и z ₃ = 1, соответственно. Оба двойных неравенства удовлетворяются. Следовательно, вектор v 1 = ( 1, - 1, - 1 ) успешно прошел проверку, так как определяет предельные последовательности у „ •

• 6)    Используя вектора, которые прошли проверку, восстановим по правилам (67) -(68) биполярные последовательности Ф ^:

  - Для вектора v 1 = ( - 1, — 1,1 ) :

• •    прямая последовательность ф 11 = ( - 1,1, - 1, - 1 ) ;

• •    инвертированная прямая последовательность ^Ф 1,₂ = ( 1, ^{- 1,}1,1 ) .

  - Для вектора v ₁ = ( 1, - 1, - 1 ) :

• •    прямая последовательность ф ₂₁ = ( - 1, - 1,1, - 1 ) ;

• •    инвертированная прямая последовательность ф 2,2 = ( 1,1, - 1,1 ) .

Видно, что последовательность ф ₂₁ получается из последовательности ф 1 1 путем обращения порядка всех элементов, тогда как последовательность ф _{2 2} получается из ф 1 1 путем обращения порядка элементов с последующим инвертированием их значений. А так как последовательность ф 1 ₂ получается из последовательности Ф 1 1 путем инвертирования значений всех элементов, то, получается, что все три последовательности ф ₁₂ , ф ₂₁ и ф ₂₂ можно получить из ф_1р

• 7)    Теперь по последовательностям ф 1 1 , ф ₁₂ , ф ₂₁ и ф ₂₂ , в соответствии с правилом (9), вычислим биполярные последовательности, которые являются предельными:

Y „,_ц = ( - 1,1,1, - 1, - 1,1, - 1,1 ) ,

Y „_д,2 = ( 1, - 1, - 1,1,1, - 1,1, - 1 ) ,

Y „,2_Д = ( - 1,1, - 1,1,1, - 1, - 1,1 ) ,

Y „ ,2,2 = ( 1 - 1,1, — 1, — 1,1,1, — 1 ) .

Все эти четыре последовательности имеют одну и ту же автокорреляционную функцию f _АКФ ( y „ , k ) :

• ^{- 1,2}, ^{- 1,}0, 1, - 2, - 3, 8, ^{- 3, - 2,}1,0, - 1,2, ^- 1.

• 5.    Метод    построения предельных биполярных

последовательностей с использованием порождающих функций. С ростом величины N _φ возрастает и мощность множества V ₁ (69) последовательностей-кандидатов, среди которых находятся те, которые связаны с предельными последовательностями у „ ■ Поэтому если найти функциональную зависимость между предельными последовательностями и значениями специальных функций, которые далее называются порождающими, то можно будет сразу определять некоторое подмножество предельных последовательностей для любого заданного значения N _φ (без необходимости выполнения поиска предельных последовательностей на основе рационального перебора).

Каждой биполярной последовательности φ (11) можно сопоставить целое неотрицательное число a , по следующему правилу:

N φ

i =1

N а = ^

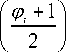
Например, биполярной последовательности ф = ( 1, - 1, - 1, - 1,1 ) , будет сопоставлено число а = 17.

Среди целых неотрицательных чисел a , в контексте решения задачи нахождения предельных последовательностей у „ , особый интерес представляют такие целые неотрицательные числа, которые соответствуют последовательностям φ , лежащим по правилу (9) в основе предельных последовательностей у „ • Например, когда N _ф = 5, тогда такие целые числа а образуют последовательность: 5,9,11,13,18,20,22,26. Видно, что минимальным среди них является число 5, значит, числа с 1 по 4 не связанны с предельными последовательностями.

Целое неотрицательное число a , соответствующее биполярной последовательности φ , определенной равенством (11) и имеющей длину N _φ , которая позволяет получить в соответствии с правилом (9) биполярную последовательность, которая является предельной последовательностью у „ , можно вычислить с помощью следующей рекуррентной функции:

f . ( N ф и

f , ( N _p - 1 ) , если N ф e { 3,6,9, ^ } , 2f 1 ( N ф - 1 ) , если N _ф e { 4,7,10, ^ } , 2f 1 ( N ф - 1 ) + 1, если N , e { 2,5,8, ^ } , 0, если N ф = 1.

Например, пусть N _ф = 19, тогда:

a = f (19 ) = 2f (18) = 2 (f (17)) = 2 (2f (16) +1) = = 2 (2 (2f (15)) +1) = ...= 2730.

В двоичном представлении в девятнадцатиразрядной двоичной сетке (так как N _ф = 19) это число выглядит так:

2730 ₁₀ = 0000000101010101010 2 .

биполярная

Значит, искомая биполярная последовательность будет:

^ф = (^{- 1, - 1, - 1, - 1, - 1, - 1, - 1,1, - 1,} 1, ^{- 1,}1, ^- 1,1, ^- 1,1, ^- 1,1, ^- 1 ) .

Этой последовательности φ соответствует последовательность:

Y = (^{- 1,1}, ^{- 1},1, ^{- 1,1}, ^{- 1,1}, ^{- 1},1, ^{- 1,1}, ^{- 1,1},

1, — 1, ^- 1,1,1, — 1, — 1,¹,¹, ^- 1, ^- 1,1,                           (76)

1, ^{- 1,} — 1,1,1, ^{- 1,} — 1,1,1, ^{- 1, - 1,1} ) ,

_{_______}DIGITAL INFO_{_}RMATIO_{_}N TELECO_{_}MM_{_}UNICATION TEC_{_}HNO_{_}LOGIES_{_______} у которой абсолютное значение отношения максимума к минимуму АКФ равно:

2 N φ

N — 1

—--N

3 ^φ

³⁸ = 2,92 ,

что является максимально достижимым значением, когда N _ф = 19 в формуле (26). Значит последовательность (76) является предельной последовательностью.

Важно отметить, что числа, получаемые из значения f 1 ( N _ф ) , путем инвертирования всех двоичных разрядов, путем обращения всех двоичных разрядов, а также путем обращения и инвертирования всех двоичных разрядов также соответствуют последовательностям φ , определяющим предельные последовательности у „ • Например, если такие операции выполнить с числом f 1 ( 19 ) = 2730 , представленном в 19-разрядной сетке, соответственно получатся следующие числа: 521557 , 174720 , 349567 . Этим трем числам, также как и числу 2730 (73) -(77), соответствуют предельные последовательности у „ • И все они будут иметь одинаковые автокорреляционные функции.

Когда N _ф е { 1,2,3,4 } , тогда с помощью порождающей функции f i ( N _ф ) , определенной равенством (72), можно получить все возможные предельные последовательности у _у . Однако, когда N _ф >  5, среди предельных последовательностей у „ появляются такие, которые уже не получаются с помощью порождающей функции f 1 ( N _ф ) . Так, например, при N _ф = 5 существует предельные последовательности у ^ , связанные с числами 9, 13, 18, 22, тогда как с помощью порождающей функции f 1 ( N _ф ) можно получить числа: 5, 11, 20, 26. Число 9 является вторым по порядку в этой последовательности из 8 чисел. Если проанализировать вторые по порядку числа для N _ф >  5 , можно получить вторую порождающую функцию:

f 2 ( N ф - 1 ) , если N ф е { 6,9,12, ^ } , f ( N      2f 2 ( N ф - 1 ) , если N , е { 7,10,13, ^ } , 2   "      2f 2 ( N ф - 1 ) + 1, если N ф е { 8,11,14, _ } , 9, если N ф = 5.

(78)

Функции f 1 ( N _ф ) (для значений N _ф е { 1, ^ ,10000 } ) и f ₂ ( N _ф ) (для значений N _ф е { 5, _ ,10000 } ) успешно прошли проверку на то, что они действительно вычисляют подходящие числа a , с помощью которых можно получить предельные последовательности у „ • Таким образом, с помощью порождающих функций f ₁ и f ₂ можно получать предельные последовательности в тех случаях, когда вычислительная сложность поиска предельных последовательностей в соответствии с предложенным выше методом неприемлемо велика.

• 6.    Результаты компьютерного моделирования. Выше было доказано, что абсолютное значение отношения максимума АКФ маркерной последовательности m к минимуму АКФ, когда используется предельная последовательность у _т , превышает число 2 и в пределе равно 3. В то время как абсолютное значение этого отношения, когда используется традиционная расширяющая последовательность γ _трад при построении маркерной последовательности m , с достаточно высокой точностью равно 2. Применение предложенных предельных последовательностей с улучшенными корреляционными свойствами позволяет повысить качество детектирования и, как следствие, устойчивость маркирования цифровых аудиосигналов к действию помех, преобразованиям и деструктивным воздействиям.

Важно выполнить экспериментальную оценку того, насколько применение предельных биполярных последовательностей отражается на корреляционных свойствах извлекаемого из стегоаудиосигнала маркера для наихудших (и часто реальных) условий приема, характеризующих прежде всего слепой прием. Напомним, что при слепом приеме аудиосигнал, в который внедряется маркер, неизвестен авторизованному получателю. В этом случае в процессе обнаружения и извлечения маркера из стегоаудиосигнала исходный (покрывающий) аудиосигнал становится шумом, влияющим на качество корреляционного детектирования.

Для этого необходимо, прежде всего, оценить то, насколько при слепом приеме изменяется взаимная корреляция между извлеченной из маркированного аудиосигнала последовательностью и внедренной маркерной последовательностью m при варьировании тех или иных параметров , а также провести сравнительную оценку абсолютных значений отношений максимумов к минимумам взаимных корреляционных функций (ВКФ), характеризующих эту корреляцию, для традиционно используемой последовательности γ _трад и предложенной предельной последовательности γ _∞ .

В процессе проведенного компьютерного моделирования в качестве покрывающих аудиосигналов использовались 100 популярных музыкально-песенных композиций из различных направлений музыки. Маркированные аудиосигналы не подвергались никаким дополнительным цифровым преобразованиям. Поэтому исходный цифровой аудиосигнал в условиях слепого приема выступал единственным искажающим воздействием (шумом). Варьируемым параметром была сила внедрения маркера, определяющая коэффициент масштабирования амплитуды частотной составляющей спектра Фурье блока отсчетов при внедрении элементов маркера. Оценивались два показателя – отношение сигнал-маркер и абсолютное значение отношения максимума взаимной корреляционной функции к ее минимуму. Оба этих показателя позволяли делать выводы об устойчивости (в условиях слепого приема) маркерных последовательностей, сформированных на основе предельных последовательностей γ _∞ , и традиционно используемых маркерных последовательностей, основанных на γ _трад .

Для внедрения, обнаружения и извлечения маркерной последовательности методом слепого приема использовались процедуры, предложенные в работе [24].

При формировании маркерных последовательностей m для компьютерного моделирования последовательность α представляла собой биполярную последовательность длиной 64449 элементов, получаемую в результате кронекерова произведения двух псевдослучайных последовательностей:

α= α1⊗ α2, где α1 – это биполярная последовательность Касами (длиной 1023 элемента), α2 – это биполярная последовательность Голда (длиной 63 элемента). В качестве расширяющей последовательности использовалась либо биполярная последовательность γтрад , определяемая равенством (10), соответствующая традиционному методу формирования маркерной последовательности по правилу (3), либо предельная биполярная последовательность:

Y„ = (1,-1,-1,1,-1,1,-1,1,-1,1,1,-1,-1,1,-1,1,1,-1,-1,1,1,-1, -1,1,1 - 1), соответствующая предлагаемому робастному методу формирования маркерной последовательности по правилу (12).

В результате, при использовании традиционного подхода к формированию маркерной последовательности вычисленное абсолютное значение отношения максимума АКФ к её минимуму составило:

= 2.001,

а при использовании предлагаемого подхода с использованием предельных биполярных последовательностей, это отношение равнялось:

= 2.889.

Поскольку при слепом приеме покрывающий аудиосигнал становится шумом для процесса извлечения внедренных маркеров и вычисления ВКФ, то абсолютные значения этих отношений для ВКФ будут определяться отношением сигнал-маркер, которое в свою очередь, зависит от силы внедрения элементов маркера.

Результаты компьютерного моделирования по оценке абсолютной величины отношения максимума ВКФ к ее минимуму в зависимости от основных параметров маркирования представлены в Таблицах 1 и 2. Приняты следующие обозначения столбцов таблицы: [А] – сила внедрения маркера; [Б] – среднее значение отношения сигнал-маркер (единица измерения – дБ); [В] – среднее значение абсолютной величины отношения максимума ВКФ к минимуму этой функции, характеризующей корреляцию между извлеченной последовательностью и внедренной маркерной последовательностью.

Традиционно считается [25, 26, 27, 28], что, когда отношение сигнал-маркер больше 20 дБ, тогда акустические артефакты, появляющиеся в результате внедрения маркера в аудиосигнал, будут

_{_______}DIGITAL INFO_{_}RMATIO_{_}N TELECO_{_}MM_{_}UNICATION TEC_{_}HNO_{_}LOGIES_{_______} не слышимы человеческим ухом. Поэтому при моделировании максимальная сила внедрения равнялась 0.1, что обеспечивает отношение сигнал-маркер больше 20 дБ.

Анализ полученных результатов показал, что при силе внедрения 0.1 абсолютное значение величины отношения максимума ВКФ к ее минимуму уменьшается по сравнению с этим же показателем, полученным для АКФ (2.001), почти на 0.12 (традиционное маркирование), тогда как для робастного маркирования, основанного на использовании предельной последовательности, это отличие составляет всего лишь около 0.05 (при значении для АКФ, равном 2.889). Традиционный маркер становится не отличим от белого шума, когда сила внедрения будет меньше 0.01, тогда как маркер, построенный на основе предельной последовательности, будет не отличим от белого шума только тогда, когда сила внедрения будет меньше 0.003.

Таким образом, при слепом приеме маркирование цифровых аудиосигналов с использованием предельных биполярных последовательностей, по сравнению с традиционным маркированием, не только обеспечивает большее по абсолютной величине отношение максимума ВКФ к ее минимуму, но и является на порядок более устойчивым к искажающему воздействию покрывающего аудиосигнала.

Таблица 1. Результаты моделирования для случая, когда использовалась традиционная биполярная последовательность у = (1, -1)

[A]	[Б]	[В]
0.1	22.6537914407729	1.89400133362661
0.09	23.5689087161114	1.88940377072308
0.08	24.5919137027463	1.88378546192023
0.07	25.7516863726654	1.87676523118745
0.06	27.0905201404766	1.86774872443684
0.05	28.6739760385219	1.85576203481233
0.04	30.6118656605248	1.83912315246444
0.03	33.1099713242667	1.80857006872274
0.02	36.6298991976145	1.66904242496330
0.01	42.6405797512073	1.22115540454256
0.009	43.5527289528179	1.17197219241071
0.008	44.5716571653026	1.12916956984856
0.007	45.7256236763519	1.09483301588215
0.006	47.0558026726118	1.06745248183093
0.005	48.6255673720736	1.04974406741366
0.004	50.5399521171489	1.03956744534308
0.003	52.9924466534771	1.03586059278761
0.002	56.4032438747814	1.03275100298008
0.001	62.0084277052975	1.03056260054767

Таблица 2. Результаты моделирования для случая, когда использовалась предельная биполярная последовательность

Y „ = ( 1, - 1, - 1,^{1, - 1,1, - 1,1, - 1,1,1, - 1,} — 1,1,—МД, ^{- 1,}—МД, ^{- 1,} — 1,1,1 ^- 1 ) .

[A]	[Б]	[В]
0.1	22.9756767301182	2.84137761957072
0.09	23.8908264049154	2.83731141890393
0.08	24.9138766626027	2.83226677555242
0.07	26.0737153223891	2.82584064373021
0.06	27.4126506827211	2.81737334369541
0.05	28.9962748847080	2.80570558153818
0.04	30.9344738175417	2.78840201614555
0.03	33.4332456738216	2.75516799839706
0.02	36.9550626144124	2.67636860609201
0.01	42.9756178969781	2.44763217519363
0.009	43.8907537349459	2.39680709039650
0.008	44.9137846437648	2.33405951225665
0.007	46.0735950750664	2.24683845587408
0.006	47.4124869330215	2.10918146136329
0.005	48.9960389735402	1.90539412353207
0.004	50.9341050426052	1.64397752034035
0.003	53.4325898308898	1.33580638954599
0.002	56.9535867943209	1.10082579442145
0.001	62.9697239736851	1.00904942996361

• 7.    Заключение. В статье разработан математический аппарат для поиска и построения предельных биполярных последовательностей, используемых при решении задачи робастного маркирования цифровых аудиосигналов по методу лоскута. Предельные биполярные последовательности определены как расширяющие последовательности с улучшенными корреляционными свойствами, у которых автокорреляционные функции обладают максимально возможными по абсолютному значению отношениями максимума к минимуму.

Сформулированы и доказаны теоремы и следствия из них: о существовании верхней границы минимальных значений автокорреляционных функций предельных биполярных последовательностей и о значениях первого и второго лепестков АКФ. На этой основе дано строгое определение предельных биполярных последовательностей и показано, что в пределе значение абсолютной величины отношения максимума АКФ таких последовательностей к её минимуму стремится к 3. Разработаны метод поиска полного множества предельных биполярных последовательностей на основе рационального перебора и метод построения предельных биполярных последовательностей произвольной длины с  использованием порождающих функций.

Представлены результаты компьютерного моделирования по оценке значений абсолютной величины отношения максимума к минимуму автокорреляционной и взаимной корреляционных функций исследуемых биполярных последовательностей для наихудших условий приема – слепого приема. Их анализ показал, что предложенные предельные биполярные последовательности характеризуются лучшими корреляционными свойствами в сравнении с традиционно используемыми биполярными последовательностями и обладают большей устойчивостью.