Предельные деформации термоупругих плоских конструкций с криволинейным армированием

Введение. Современные волокнистые композиты являются неоднородными анизотропными материалами. Упругость и неупругость волокнистых композитов определяется типом арматуры (стекло-, боро-, угле- и органоволокна) и матриц (полимерных, углеродных, металлических, керамических), степенью их взаимодействия в композите, а также углом нагружения относительно направлений армирования. Композиты обладают двумя уровнями неоднородности -микронеоднородностью (монослой, составленный из волокон и связующего) и макронеоднородностью (слоистая структура, составленная из монослоев, с произвольной укладкой по толщине пакета). Отсюда два направления в механике композитов: микро-и макромеханика. Сочетанию микро- и макроструктур композита в задаче оптимизации посвящена недавняя работа коллектива зарубежных авторов [1]. Для зарубежной литературы характерно наличие большого количества работ по композитам, описывающих гиперупругость при условии конечных деформаций, например [2; 3]. Структурно-неоднородная среда по своему физико-механическому поведению значительно богаче однородного материала. Разнообразие возможных ситуаций в процессе деформирования и разрушения композитов делает изучение этих материалов привлекательным для специалистов из разных областей механики твердого тела. Например, в волокнистых композитах на уровне армирующих элементов всегда имеются микродефекты - трещины, обусловленные не только несовершенством технологии, но и отступлением от идеализированной модели материала. Центральным моментом в механике волокнистых композитов является существенный учет структуры материала на уровне армирующих элементов - обстоятельство, не характерное для классической механики твердого тела. На уровне армирующих элементов создаются механические свойства материала; управляя укладкой волокон, можно в определенных пределах управлять полями сопротивления материала, «подстраивая» их под действующие усилия. Общий подход построения механики волокнистых композитов представлен в монографии [4].

В настоящее время возможности существенного прироста прочностных характеристик сталей, алюми- ниевых, титановых и магниевых сплавов практически исчерпаны, и поэтому для значительного улучшения технических параметров в объектах ответственного назначения необходимо использовать разнообразный спектр современных композитных материалов, сочетающих высокую удельную прочность и жесткость с другими ценными качествами: высокой технологичностью изготовления конструкций из них, повышенной стойкостью к агрессивным средам.

В современной аэрокосмической промышленности широко используются тонкостенные элементы из волокнистых композитных материалов. Волокнистое армирование позволяет применять новые принципы проектирования и изготовления изделий, основанные на том, что материал и изделие создаются одновременно в рамках единого технологического процесса. В результате получается изделие с новыми уникальными эксплуатационными качествами. До недавнего времени армирование осуществлялось преимущественно прямолинейными волокнами. Такие структуры армирования не могут быть эффективны для конструкций с большими градиентами полей напряжений и деформаций в зоне отверстий и переходных элементов, часто встречающихся при создании реальных объектов. В этом случае необходимо создавать конструкции со специальными криволинейными структурами армирования, согласованными с реальными требованиями эксплуатации соответствующих изделий.

Постановка задачи. В работах [5; 6] сформулирована плоская задача армированной среды в криволинейных ортогональных координатах ( ^ , ц ), которая включает уравнения равновесия, обобщенный закон Дюамеля-Неймана в условиях термоупругого анизотропного деформирования [7-9], соотношения для напряжений в волокне на основе структурной модели [10]. Пусть армирование выполнено k семействами волокон, ф m - углы армирования m -м семейством волокон ( m = 1, ..., k ), являются непрерывными функциями координат, е _m -деформация в волокне, го _m - интенсивность армирования m -м семейством волокон. Деформации в волокне определим по структурной модели [10]

2             2                          о

^S 11 l m 1 ^+S 22 l m 2 ^{+ S} 12 l m 1 l m 2 = ^S m ,

где l m I = cos ф m , l m 2 = sin ф m , a m — коэффициент линейного температурного расширения материала m -го семейства волокон; Т - заданная постоянная температура. Напряжение в волокне о _m находим по формуле

a34 = — m1 LT + стm tom sin фm cos фm ’

E m, = a-----

¹      1 — v ²

^m 2

E

= a -----, 1 + v

СТm = Em (611 cos2 фm + 6 " sln' Фm + + e12 cos фm sin фm ) + CTm ,

где E_m - модуль Юнга материала m -го семейства волокон; ст m = E_m a ^a_mT . Связь напряжений a ,j и дефор

L^T =a ^c (1 + v ) T .

При наложении дополнительных условий постоянства сечений волокон, что соответствует условиям технологического процесса, интенсивность армирования to _m удовлетворяет следующим соотношениям [11]

маций риала

С ) для запишем

неоднородного армированного мате-k в виде стij = a ст ) + Z стт tomlmik) ’ m=1

c где напряжения в связующем стг) определим по фор-

мулам с учетом поля температур [7]:

ст С

E

(1 -v ² )

E

ст) = (1 + V)S ij ’ j = 3 - i ’ i = 1 2’

где E , v , a ^c — соответственно модуль Юнга, коэф

фициент Пуассона и коэффициент линейного темпе

ратурного расширения связующего материала;

k

a = 1 —Z® m — m=1

удельная интенсивность прослоек

связующего между армирующими слоями. Напряжения с учетом структурных характеристик имеют вид [5; 6]

^ст 11 = ^a11 ^S 11 ^{+ a}12 ⁶ 22 ^{+ a}12 ⁶ 12 ^{+ a} 14 ’ ^ст 22 = ^a12 ⁶ 11 ^{+ a} 22 ^S 22 ^{+ a} 23 ^S 12 ^{+ a} 24: ^ст 12 = ^a13 ⁶ 11 ^{+ a} 23 ^е 22 ^{+ a} 33 ^е 12 ^{+ a} 34 ^.

Приведем коэффициенты в (3) a j , i = 1,3, j = 1,4,

учитывающие все структурные характеристики и влия

ние поля температур:

* m

• ^a11 = ^m 1 + Z ^Em ^to m ^cos 4 ф m ’

m = 1

*

m

• a12 = Vm1 + Z Em tom sin2 фm COs2 Vm ’

m = 1

*

m

• a13 =Z Em tom cos3 фm sin фm ’

m = 1

* m

• ^a 22 = ^m 1 ⁺ Z ^Em ^to m ^sin 4 ф m ’

m = 1

*

m

• a23 =Z Em tom cos фm sin3 фm ’

m = 1

*

m

• ^a 33 = ^m 2 ⁺ Z ^Em ^to m ^sin 2 ф m ^COs 2 ф m ’

m = 1

• ^a 14 =^{— m} 1 L^T +^ст m to m ^cos 2 ф m ’

• a 24 = — m 1 L T + ст m to m sin ² ф _m ,

— (H2tom COs фm ) + ^(H1tom sin фm ) = °.

Sc,Sp

Интенсивность to _m определяется из (5) после вычисления углов армирования при задании уравнений конкретных траекторий армирования и начальных условий выхода арматуры. В работе [12] построены изогональные траектории к данным семействам плоских кривых, что расширяет многообразие непрерывных криволинейных траекторий.

В рамках прямой задачи (известна структура армирования) замкнутая разрешающая система формулируется относительно компонент тензора деформации, поставлена краевая задача в криволинейных координатах [5; 6]. Коэффициенты системы и краевых условий содержат все структурные характеристики композита: заданные углы армирования, интенсивность армирования, механические характеристики материалов связующего и арматуры. В случае осесимметрической задачи (концентрическое кольцо) армирование проводится одним, двумя и тремя семействами волокон, представляющих собой алгебраические спирали и им изогональные траектории [12]. Разрешающая система формулируется в перемещениях и приводит к краевой задаче для системы обыкновенных дифференциальных уравнений относительно радиального и окружного перемещений. Особенность полученной системы состоит в том, что она является системой, неразрешенной относительно старшей производной. На основе монографии [13] для такой системы разработан новый эффективный численный метод, учитывающий особенности армированной среды и уменьшающий ошибки численного счета [14]. Такой подход позволяет решать задачи о криволинейно армированных вращающихся дисках, являющихся элементами конструкций ответственного назначения [15].

Анализ признака «расход арматуры». Для анализа эффективности конструкции вводится характеристика армирования - расход арматуры [11]. Обозначим ее символом В . Для армирования кольцевой пластины двумя семействами волокон в полярной системе координат расход арматуры определяется по формуле

R 2

B = J R ( to 1 ( R ) + to ₂ ( R )) dR , R 1

где R - линейный размер пластины, R е [ R 1 , R ₂ ]; ю 1 - интенсивность армирования первым семейством

волокон; ю₂ — интенсивность армирования вторым семейством волокон. Проводится анализ зависимости B от начальных стадий технологического процесса -начальных интенсивностей армирования двумя семействами армирующих волокон для различных структур армирования.

Интенсивности армирования для данных структур найдены в аналитическом виде как решение задачи Коши дифференциальных уравнений, представляющих условия постоянства сечений волокон (5). Они определяются по следующим формулам для армирования семейством логарифмических спиралей и семейством «спицы велоколеса»:

« 10 4R

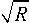
« 20 V R ( R ² - ( R i sin 0 0 ) ² ) ⁴

« 2 =-------------------Г"

RK ( R ² - ( R i sin 0 0 ) ² ) ⁴

Для армирования вдоль траекторий семейства спирали Архимеда интенсивность имеет вид

« 30 V ^R i + ^R tg %

«3 =-------1     2

^R V¹ + tg ² ^ 0

, для траекторий, изогональ-

ных к семейству логарифмических спиралей, интенсивность армирования задается формулой

« ₄

« 40 V ^R 1

---;=—, где

V R

« 10 , « 20 , « 30 , « 40

начальные ин

тенсивности армирования семействами волокон;

0 ₀ , р ₀ - начальные углы выхода арматуры.

На рисунке в осях интенсивностей армирования « I , « ₂ показано влияние выбранных начальных условий технологического процесса (в соответствии с таблицей) на признак В «расход арматуры» для различных криволинейных структур армирования.

Развиваемый подход в рамках единой вычислительной схемы позволяет управлять свойствами волокнистого композита, создавать эффективные и рациональные проекты для плоских конструкций как элементов конструкций ответственного назначения.

Сформулированная плоская задача армированной среды в криволинейных ортогональных координатах позволяет решать и обратную задачу по определению эффективной рациональной структуры, если к ней добавить требования равнодеформируемости волокон или равнотрещиностойкости в связующем по критерию Баландина [16].

Постановка задачи об армированной пластине с равной трещиностойкостью связующего. Рассматривается пластина, полученная из набора прослоек связующего и прослоек арматуры, симметричных относительно срединной поверхности. Прослойки тонкие, поэтому реализуется плоское напряженное состояние. Пусть температура T = const постоянная по толщине пластины.

Запишем полные деформации ^en, ^е 22 , ^е 12 в декартовой системе координат как сумму механических и тепловых деформаций:

mech с_Т mech cj mech cj

^Ь 11 = ^Ь 11 ^ ^u T , ^ь 22 = ^ь 22 ^ и. T , ^ь 12 = ^ь 12 ^ и. T .

Параметры технологического процесса

« 01 — начальная интенсивность армирования первого семейства волокон	« 02 — начальная интенсивность армирования второго семейства волокон	0 0 — начальный угол выхода семейства «спицы велоколеса»
0,3	0,3	л /4
0,05	0,376	л /12
0,1	0,318	5 л /4
0,51	0,18	7 л /4

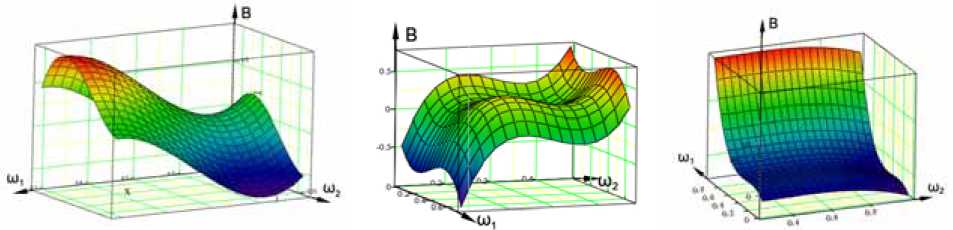
б

в

Расход арматуры В (ось аппликат) для: а - структуры армирования «семейство логарифмических спиралей» и «спицы велоколеса» ; б - структуры «семейство спиралей Архимеда» и «спицы велоколеса»; в - семейства логарифмических спиралей и им изогональных траекторий

Потенциальная энергия в прослойках изотропного связующего равна ттт _ c mech , с mech , с mech

W = ⁰ 11 ⁸ 11    +^ 22 ^ 22   ⁺ 2 ^ 12 ^ 12 ’

где напряжения в связующем заданы соотношениями

8 ,              . , 8.

—(№1cos Ф1)+ — (№1 sin Ф1) = 0, 8x8

8 ,               . , 8.

— (№2 cOs Ф2) + — (№2 sin Ф2) = 0. 8x8

_ с     1 _mech , j _mech

⁰ 11 = а _пе_п  ⁺ a 12 S 22   =

= dпеп + d12822 - (d11 + d12)aT, с — /7 Cmech л mech _ 022 = d11822   + d12S11   =

= ^d 12 ^S 11 ^{+ d} 11 ^S 22 ^{- ( d} 11 ^{+ d} 12 ^{) a T} ’

⁰ 12 = ^d 13 ^S 12 -

С учетом (6) потенциальная энергия запишется как

W = ^b 11 ^S 11 ^{+ b} 12 ⁸ 22 ^{+ b}13 ⁸ 12 ^{+ b} 14 ⁸ 11 ⁸ 22 ⁺

^{+ b} 15 ⁸ 11 ^{+ b}16 ⁸ 22 ^{+ b} 17 = W c = ^const

Коэффициенты в (7) для изотропного связующего имеют вид

г, _ г, _ Е к _ Е b11 = b12 =     2 ’ b13 =     , V

1 -V ²        2(1 + v )

^b 14 =

2 v Е

1 - v ² ’

b 15

2 a ^cT v E

1 - v ² ’

,      2 Ea cT , b16 =-  ---T’ b17

1 -v ²

2 ( a ^cT ) ² E

1 - v

Совокупность уравнений (7)-(10) позволяет решить задачу о нахождении направлений армирующих слоев рассматриваемой пластины в условиях термоупругого деформирования, т. е. решить обратную задачу с дополнительным условием равной трещино-стойкости связующего. При введении начальных условий на интенсивности армирования и краевых условий на внешнем контуре получаем замкнутую систему по определению траекторий армирования.

Заключение. Развиваемый подход в рамках единой вычислительной схемы позволяет управлять свойствами волокнистого композита, создавать эффективные и рациональные проекты для плоских конструкций как элементов конструкций ответственного назначения.

Acknowledgments. The work was performed with the financial support of the Russian Foundation for Basic Research (grant №14-01-90400 Ucr_a).

Условие совместности деформаций в декартовой системе координат имеет вид

52еп 8 2S22

„ 2 + „ 2 = n п ■

8у2    8x2