Предельные характеристики оптико-механических систем со сканированием

В основе работы современных оптикомеханических систем со сканированием заложен оптико-корреляционный принцип определения направления на оптический излучатель. Последний заключается в измерении рассогласования во взаимном положении изображения излучающего объекта и изображения его маски при непрерывном колебании или пульсации последней по измеряемой координате [1]. Технологически сам процесс сканирования условно можно разбить на два этапа. На первом этапе в режиме поиска производится вывод маски на заданную координату за счет вращения или шагового перемещения ее с помощью исполнительного двигателя углового движения, а на втором – осуществляется колебательное или пульсирующее движение относительно оптической оси.

Однако, как известно, получение периодических видов движения маски требует при использовании серийных электродвигателей наличия механического преобразователя движения, что существенно ограничивает частоту сканирования, вносит существенный вклад в погрешность ориентатора, снижая как его надежность, так и надежность всей системы в целом [2, 3].

Данные недостатки сканирующих систем могут быть существенно снижены, если в качестве

Законы движения маски объекта

Таблица 1

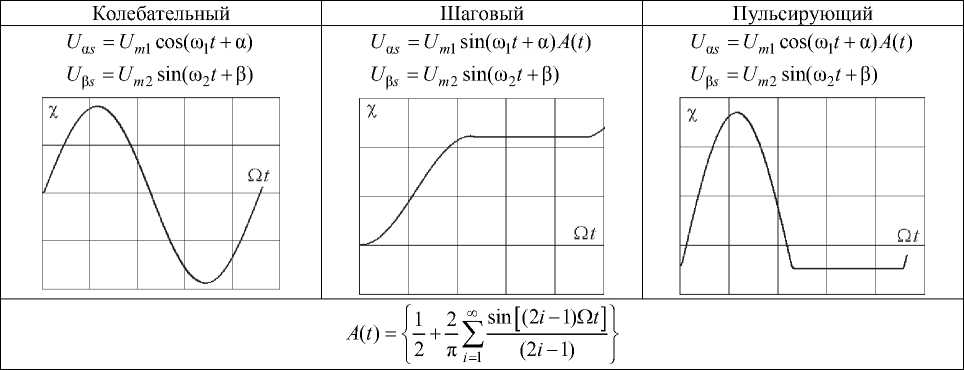
Примечание. U m 1 , U m 2 – амплитудные значения фазных напряжений; ω 1 , ω 2 , α, β – круговые частоты и начальные фазы напряжений питания; Ω – частота шага или сканирования; А ( t ) – импульсная функция.

исполнительного двигателя движения маски объекта использовать двухфазный асинхронный двигатель (АД), работающий непосредственно в режиме периодического движения за счет фазовой модуляции питающих напряжений или токов с использованием прерывания по одной из его обмоток [4–6]. Как показывает практика, такие без-редукторные электроприводы обеспечивают плавное регулирование на ходу амплитуды, частоты и фазы практически во всей или части области сканирования и, кроме того, позволяют создавать многокоординатные движения рабочего элемента самых разнообразных законов.

В соответствии с [7] в табл. 1 представлены фазные напряжения статорных обмоток асинхронного двигателя для формирования требуемых периодических законов движения χ( t ).

Функциональная схема электропривода сканатора

На рис. 1 представлена функциональная схема электропривода (ЭП) оптико-механического ска- подвижного элемента двигателя χ(t) в поле обзора осуществляется в соответствии с состояниями ключей SA1 и SA2 (рис. 1). С целью устранения влияния девиации частоты сети на частоту сканирования задание частоты Ω осуществляется от прецизионного источника питания, согласно тому, как это было предложено в [8].

Предельные характеристики электропривода сканатора

Предельными характеристиками электродвигателя сканатора будут являться поверхности его предельного динамического состояния, которые определяются либо в сило-кинематических

, dx d n x,_м ам^ dM,

„ М ^d ( X ^M эм )   dⁿ ( X ^M эм ) ■ _M   ^dM эм    ^d"^M эм

χ эм, dt , ... dtn;Mэм, dt ,... dtn координатах.

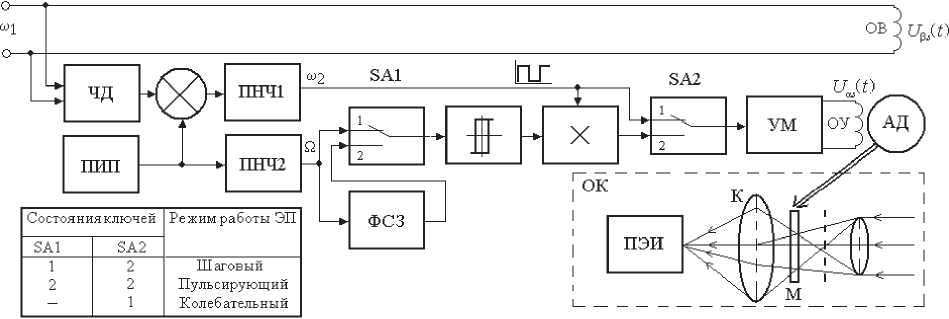
Рис. 1. Функциональная схема электропривода оптико-механического сканатора

натора, выполненного на базе двухфазного АД, работающего непосредственно в режимах периодического движения согласно алгоритмам, представленным в табл. 1.

Она содержит: частотный демодулятор (ЧД), преобразующий частоту сети ю 1 в пропорциональный уровень постоянного напряжения; прецизионный источник питания (ПИП), выполняющий роль задатчика частоты шага или частоты сканирования Ω; сумматор, формирующий напряжение, пропорциональное частоте ю ₂ = ® 1 +Q; два преобразователя «напряжение-частота» (ПНЧ1, ПНЧ2); компаратор; электронные ключи SA1 и SA2; фазосдвигающее звено (ФСЗ); усилитель мощности (УМ) и оптический коррелятор (ОК). Последний включает в себя конденсатор (К), формирующий корреляционное световое пятно на фоточувстви-тельную площадку приемника энергии излучения (ПЭИ) и маску объекта (М).

Формирование требуемого закона движения

Они совместно с нагрузочными характеристиками и целевой задачей позволяют осуществлять выбор или проектирование исполнительного двигателя, например, как это представлено для электродвигателя постоянного тока в работах [9, 10].

Так, при токовом питании первичного и вторичного элементов исполнительного двигателя, когда он работает в режиме источника периодического силовозбуждения, предельная характеристика будет представлять собой плоскость, перпендикулярную к оси М эм на уровне его максимального значения М эм, max . Такой подход является корректным, так как в этом случае развиваемое двигателем усилие не зависит от параметров движения.

Для получения предельных характеристик сканирующей системы, используемой в качестве источника периодического перемещения или мощности, воспользуемся системой уравнений обобщенного электромеханического преобразователя энергии, записанной через потокосцепления [10]:

U a s = Y r Y a s - Y m Y a r + d ^ a s । dt ;

Ups = Yr Y- s -Ym Y- r + d Y- s / dt;

Uar = Ys Yar - Ym Yas + d Yar I dt + ^Ypr;

‘ U p r = Y s Y p r -Y m Y p s + d Y p r I dt - r ; (1)

Mэм = Y m (YpsYar -Yas Yp r ) = = Mн (J^dt, ^, d^ / dt), где Uas, Ues, Uar, Uer; Yas, Yes, Yar, Yer - соответственно напряжения и фазные потокосцепления в обмотках статора и ротора по осям a и в; £ -обобщенная скорость подвижного элемента скана-тора; Мэм и Мн – обобщённые электромагнитное усилие и нагрузка; yr, Ys, Ym, Y’m — коэффициенты, определяемые выражениями:

^Y _r = L a _rR s ¹ ( L _a s^L _{a r} ^{- M} 2 ) ^;

Y m = MR_S I ( L a _SL a r - M 2 ) ;

ys = lasRr । (lasLar -m2);

Y m = MR r I ( L a s L a r - M ² ) .

Здесь R s , R r , L α s , L α r – активные сопротивления и полные индуктивности фазных обмоток; M – взаимоиндуктивность между статорными и роторными обмотками двигателя.

Проводя четырехкратное дифференцирование М _эм во времени t и выразив производные от пото-косцеплений через коэффициенты системы (1), можно записать

M эм

= Y m ( Y p s Y a r

Y a s Y p r ) ;

dM эм 22

, „ = A 1,n ^Y a s ⁺ A 2, n ^Y B s ^{+ n}

<+ A 3, n Y a r + A 4, n Y ^ r +

+A5, n (YpsYar -Yas Yp r ) +

+ А б, n ( Y a s Y a r +Y p s Y_p r ) + A 7, n

где n = 1, 2, 3, 4 – порядок дифференцирования, А i,n – коэффициенты, определяемые параметрами двигателя, источниками питания и движения подвижного элемента двигателя.

Если коэффициенты системы (2) определены через максимальные значения напряжений питания обмоток исполнительного двигателя, то в параметрическом виде система представляет собой предельную характеристику с параметрами Y_{a s} , Y p _s , Y_{a r} , Y p _r . Однако получить аналитически точную предельную характеристику в явном виде невозможно, поскольку для определения из четырех последних уравнений системы (2) потокосцепле-ний через производные от электромагнитного момента с целью последующей подстановки их в первое уравнение необходимо решать алгебраическое уравнение восьмой степени.

С целью облегчения решения поставленной задачи предлагается предельную характеристику искать в виде следов на плоскостях М эм - ^ (предельная механическая характеристика), М _эм – d М эм / dt (предельная пусковая характеристика), d М _эм/ dt - ^ (предельная характеристика холостого хода) и т. д., поскольку соответствующие переменные в системе уравнений (2) приравниваются к нулю. Для сопоставления предельной характеристики двигателя с нагрузочной поверхностью или линией, последние также представляют в виде следов или проекций на тех же плоскостях.

Однако если закон движения сканирующей системы представляет собой достаточно сложное движение, такое сопоставление может внести существенную ошибку, особенно в том случае, если нагрузочная поверхность или линия частично находится вне объема предельной характеристики, а на следах это не проявляется. Очевидно, что тогда представление предельной характеристики следами неприемлемо и поставленную задачу следует искать с помощью численных методов математи- ческого моделирования.

Установлено, что процесс построения предельной характеристики можно существенно упростить, если считать, что исполнительный двигатель спроектирован «корректно». Тогда при максимальных допустимых значениях напряжений питания в нем формируется круговое магнитное поле, максимальное по величине и не насыщающее магнитопровод. В этом случае максимальные значения потокосцеплений обмоток статора и ротора (Ysm, Yrm) будут определяться как

Y 2 m =Y a s + Y p s - const,

Y 2 m =Y a r +Y p ² r - const.

Исходя из вышесказанного и введя обозначе- ния p = YrmIYsm, Ys = YasIYsm, Yr = YarIYsm, первые четыре уравнения системы (1) принимают вид

Y r s + Y mLr +

t

_Y ^{d Y} s = s dt

^- Y r

+

+y m^ (p^{2 Y 2})( 1 -^Y2) + U⁵- ^ ( 1 ^{Y :}) ;

Y d^r = -v fц2 -Y2'l + Y /fl-Y2! + А r dt Y s (p 1 r ) + Y m 1 s (1 1 s ) +

+;» r        + U ^ r - ,/(1 -^) .

sm

Исключив из системы (3) производные по по-токосцеплениям, после алгебраических преобразований получим

«1* 2 - bl (*r )*s + C (*r) f3^+dl - 0;

• • a ₂ * 2 - b ₂ ( * s ) * _r + c ₂ * _r^ ц ² -* 2 +       (4)

+d2 (*s ) = ° где значения коэффициентов системы (4) представлены в табл. 2.

Данные уравнения позволяют построить семейство кривых * s ( * _r ) или * _r ( * _s ) для различных

d х   dn х параметров движения х,     ,--- .... Для этого dt    dtn уравнения (4) преобразуются к виду (5)

На нем функциональные зависимости * s ( * _r ) и * _r ( * _s ) построены для электрической машины, имеющей следующие параметры в относительных единицах: R s = 0,084, R r = 0,088, L_s = 0,034, L_r = 0, 0 36, M = 0,032 при гармоническом законе сканир о вания.

После подстановки полученных значений в с и стему уравнений (2), з аписанную в относительных переменных * s и * r , получают предельную характеристику исполнительного двигателя.

Как правило, для большинства случаев достаточно рассмотреть только две силовых к оординаты

, Тbl (*r) - C (*r) ± Vbl2 (*r) + C (*r)(2bl (*r) + 4ai) + c2 (*r) - 4«id11

• * s ( * r ) -                                                                                    ^J ;

2al 11 bl (*r) + Cl (*r) ± Vbl2 (*r) + Cl (*r)(2bl (*r) - 4«l) + Cl2 (*r) - 4«ldl I

г /------------------------------------------------------------1                (5)

_ b 2 ( * s ) - 2 C 2 ± bb ² ( * s ) + 2 b 2 ( * s ) C 2 + C ² - 4 a 2 d 2 ( * s ) + 4 a 2 C 2 Ц ² J

* r ⁽* s > -2^ 2

[ b 2 ( * s ) + 2 C 2 ± V b ² ( * s ) + 2 b 2 ( * s ) C 2 + C ² - 4 a 2 d 2 ( * s ) - 4 a 2 C 2 Ц ² J

Таблица 2

К определению коэффициентов системы уравнений (4)

a l	l + Y r	a 2	—2 y s
b l ( * r )	Y m * r + U a s / * sm	b 2 ( * s )	Y‘ m * s + U a r / * sm — ^ (l- * 2 s )'■"
C l ( * r )	Y m ( Ц 2 — * 2 r )0,5 + U в s / * sm	C 2	- ^
d l	Y r	d 2 ( * s )	Y s Ц 2 - (l - * 2 s )0,5 ( Y m * s - U 3 r / * sm )

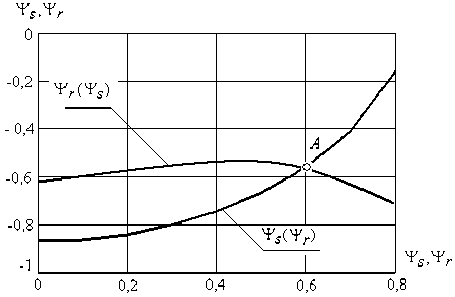
Следует иметь в виду, что кривые * _s ( * _r ) и * _r ( * _s ) в системе уравнений (5) не являются обратными функциями относительно друг друга. Кроме того, каждая из определяемых величин может иметь до четырех решений. Однако, исходя из физического смысла, при расчетах * s ( * r ) и * r ( * s ) следует учитывать только вещественные значения переменных. Такой подход приводит к определению лишь одной, максимум двух пар значений * s и * _r , как точки пересечения их кривых (точка А ). Рис. 2 иллюстрирует данное замечание.

M _эм, dM эм или M _эм, эм ^эм , которые выбирают- dt dt ²

ся в соответствии с заданием сил сопрот и вления.

Например, для первой пары координат уравнения, дающие совместно с (5) предельную характеристику, будут иметь вид

Mэм - Ym*sm [V' * VЦ2-*2 -*s VЦ-*2 1;

* s ( y r + Y s ) V Ц ² -* ²

^^^^^^B

U 3 r

sm

+

Рис. 2. К определению совместного решения кривых * _s (* r ) и * r (* _s )

dM эм dt

+* r

= Y Y^{2 2}

^Y m sm

(Yr +Y s x/l-*2 + U^

* _sm

+^* s * r + U^r-

_ * sm

^^^^^^B

-^vi-*f v *-*2 - U^ >1 ц2-*2 * sm

Заключение

Использование в оптико-механических системах со сканированием двухфазного ас и нхронного двигателя, работающего н е посредственно в режиме периодического движения за счет ф азовой мо-

дуляции питающих напряжений, позволяет существенно повысить точность и плавность динамических режимов ориентатора путем исключения дополнительных механических звеньев преобразования движения. При этом предельные характеристики обобщенного электродвигателя периодического движения в общем случае могут быть найдены только с помощью численного решения системы уравнений, описывающих работу электромеханического преобразователя энергии. Однако если считать электромагнитное поле исполнительного двигателя круговым, то при максимальных параметрах источников питания может быть использован графо-аналитический метод, основанный на результатах, полученных в настоящей работе.