Предельные распределения числа деревьев заданного объёма в лесе Гальтона - Ватсона с ограниченным числом вершин

Рассмотрим докритический или критический процесс Гальтона - Ватсона, начинающийся с N частиц. Очевидно, что такой процесс распадается на N независимых подпроцессов с одной начальной частицей. Бесконечное множество всех возможных траекторий процесса представляет собой множество лесов, состоящих из N корневых деревьев с помеченными вершинами, а распределение вероятностей на этом множестве естественным образом индуцируется ветвящимся процессом. В [13] получены предельные распределения основных характеристик случайного леса Гальтона - Ватсона, в котором число вершин равно N + n .

Будем считать далее, что число прямых потомков каждой частицы процесса Гальтона - Ватсона имеет распределение Пуассона с параметром X , 0 <  X < 1. Обозначим через $ 1 , .., $ N число частиц, существовавших за все время эволюции в подпроцессах, начинающихся c частиц 1, ..., N соответственно. Легко видеть, что $ 1 , .., $_N независимы и определяют объемы деревьев леса Гальтона - Ватсона за все время эволюции процесса. Заметим, что подмножество траекторий такого процесса при условии $ 1 + . + $_N = N + n совпадает с множеством лесов с помеченными вершинами, содержащих N корневых деревьев и n некорневых вершин, свойства таких лесов изучались в [5], [6], [7] с помощью обобщенной схемы размещения [2], [3]. В работах [10], [11] предложен аналог этого метода, где сумма независимых одинаково распределенных случайных величин ограничена сверху. Используя данную модификацию, в [9], [12] получены предельные распределения числа ячеек заданного объема

и максимального заполнения ячейки в схеме размещения частиц по ячейкам с пуассоновским распределением заполнения ячеек.

Известно [8], что введенные выше случайные величины $ 1 ,., $_N имеют распределение Бореля - Таннера:

Рк = P { £ = ^{к } X}

к - 1

¹— e ^{- Xk} ,

к = 1 , 2,..., 0 <  X <  1, i = 1,..., N .

Далее мы будем рассматривать подмножество траекторий процесса, удовлетворяющих условию $ 1 ⁺ . ⁺ $ N ^ П .

Обозначим через цг случайную величину, равную числу деревьев, содержащих ровно r вершин.

В теоремах 1 и 2 найдены предельные распределения случайной величины ц_г при N -^да.

Теорема 1 . Пусть N^» и выполнено одно из следующих условий:

• 1.    r ^w, (1 - X ) N ^ Y , 0 <  Y < ”, n / N - C > 0;

• 2.    r ^w, X - X 1 > 0,

• 3.    r - 3, X^ 0, NX ³ ^да, N - n (1 - X ) < C( XN) ^1/2 , где C - 0;

• 4.    r = 2, X^ 0, NX ⁶ ^да, ( n (1 - X ) - N )/( XN) ¹² ^да.

(1 - X ) N ^да, (1 - X ) ^1/2 ( N - n (1 - X )) <  CNⁿ, где C - 0;

Тогда

P ^ M r = ^k } = ^Г e ^- Np r ( 1 ⁺ o ( 1 ) )

равномерно относительно целых неотрицательных к, для которых ( k-Np)/(Np) ^1/2 лежит в любом конечном фиксированном интервале.

Теорема 2 . Пусть N^« , Np_r (1- p) ^да и выполнено одно из следующих условий:

(pNxr/2) слабо сходится к стандартному нормальному распределению.

Доказательство. Используя равенства

• 1.    r = 1,2, X^ 0, NX ^{2 r +2} ^да, (n (1- X )- N )/

  / ( XN) '^/;

• 2.    r > 3, Х^ 0, NX ^:^/, N - n (1- X ) < C( XN ) ^1/2 , где C > 0;

• 3.    r ^да,0 < X , <  X < X ₂ < 1, N - n (1- X ) <  C V'. где C > 0;

• 4.    r > 1 фиксировано, 0 < Х ₁ <  X <  X ₂ < 1, ( n (1- X ) - N)/N/²^;

• 5.    r > 2 фиксировано, X^1-1/r, | n (1- X ) - N |/ N ¹/² <  C , где C > 0;

• 6.    X^ 1, (1- X ) N ^да, (1- X ) ^1/2 ( N - n (1- X )) < O'. где C > 0;

m = (1- X ) ^-1 , о ² = X (1- X ) ^-3 ,           ₍₂₎

E513 = (1 + 2X) (1-X)-5              1 J и формулу Тейлора, находим, что для характеристической функции у (t) случайной величины (ZN - mN)/(о№/2) выполнено соотношение lnу (t) = -12/2 + O ((NX3 (1-X)) -1/2) = -12/2 + О (1) при любом фиксированном t. Отсюда и из теоремы непрерывности следует утверждение леммы.

Лемма 3. Пусть N ^да, (1- X ) N ^ Y , где Y - некоторая неотрицательная постоянная. Тогда распределение суммы Z_N / N слабо сходится к распределению вероятностей с плотностью

( \        ¹ f      Y ² x    1 1

g ( x ) =       ^ex P 1 Y ^— —7ГГ -       ⁽³⁾

X V 2 ^ х    [     2 2 x J

(1- X ) N ^ y , 0 <  Y < ”, n / N ² >  C > 0;

r > 2 фиксировано, X = 1-1/ r ,

( n - Nr ) /№/О-да, n = Nr + o ( N ^2/3 ).

Тогда r т          1 + О 1 )           2

P { ^ r = k } = ,----- e" ^{u /2} V ² ^ ^NP r ( 1 - P r )

равномерно относительно u = ( k-Np_r )/( Np _r (1 —p_r )) ^1/2 в любом конечном фиксированном интервале.

Для доказательства теорем 1 и 2 нам потребуются вспомогательные утверждения, которые приводятся ниже в леммах 1-5.

Лемма 1. Для к = 0,1, .„, N справедливо равенство

Доказательство. Следуя доказательству леммы 2.4.4 [3], нетрудно показать, что для характеристической функции ф ( t ) случайной величины 5 ₁ при любом фиксированном t выполнены соотношения: N lnф ( t / N ² ) ^- (-2 it ) ^1/2 при X = 1 и N ln ф (t / N² ) ^ Y - ( Y ²-2 it ) ^1/2 при Х+1. Отсюда и из теоремы непрерывности получаем утверждение леммы, поскольку exp { y - ( Y ² -2 it ) ^1/2 } является характеристической функцией распределения вероятностей с плотностью (3) [4].

Лемма 4. Пусть s ^да, sX ⁶ (1- X ) N ^да при r = 2 и sX ³ (1- X ) N ^да при r +2. Тогда распределение случайной величины ( Z_s ^{( r} ) - ms)/(os ^1/2 ) слабо сходится к стандартному нормальному распределению.

P { ^ r = к } =

² N " V ^к ,

к /а       \N— к p (1 — pr )

^P { ^ N-к ^{5 n —} кг }

P { ^ v 5 n }

^{где z}N = ⁵ 1 ⁺ ^ ^{+ 5}N , ^— к = P ^{r )} + ^ + P r — к , ^неза висимые случайные величины 5 ₁ ^{( r} ^.., 5_N ^{( r} ) имеют распределения

P {5(r>= 1} = P {51 = 1151+r}, i = 1, _, N, 1 = 1, 2,

Доказательство. Введем случайные величины п ₁, • • -, n N , равные объемам деревьев в рассматриваемом лесе Гальтона - Ватсона. Очевидно, что справедливо равенство

^{P {} П 1 = ^к 1 , -, n N = ^к^ ^} =

= P { 5 1 = к 1 ,..., 5 N = к_м | 5 1 +    + 5 N <  n }.

В [10] показано, что отсюда следует утверждение леммы.

Обозначим m = E51, о2 = D51, mr = E51 (r), ог2 = D51 (r).

Лемма 2. Пусть N ^да, X ³ (1- X ) N ^да. Тогда распределение случайной величины ( Z N - mN)/

Доказательство. Обозначим через ф_г (t ), y_r ( t ) характеристические функции случайных величин 5 ₁ ^{( r} ) , ( Z_s ^{( r} ) - m r s )/( o r s ^1/2 ) соответственно. Спра-

ведливо равенство:

V _r ( t ) = exp - —

С помощью (1) несложно показать, что mr = (m - rp)/(1-p),

°_r² = ^{o 2 (1-} p)^-1 (1- p_r ^- p_r^{(m - r ) 2 / o 2 )},    ⁽⁵⁾

E ( 5 1^{( r ))3} = (1- p r )- ¹ ((1 + 2 X )(1-X) ^-5 - r³p).

Учитывая (1), (2), находим, что имеют место соотношения:

при X ^0

m 1 = 2(1 + о(1)), mr = 1 + о(1), r > 2, о 12 = 3X/2(1 + о(1)), о22 = 6X2(1 + о(1)),(6)

Or2 = X (1 + о(1)), r > 3, при 0 < X 1 < X < X2 < 1

0 < C1 < mr, or2 < C2 < да, r > 1,(7)

при Х^-1

mr < C3(1-X)-1, Or2 = C4(1-X)-3 (1 + о(1)),(8)

здесь и далее через C 1 , C ₂ , C ₃ , ... обозначены некоторые положительные постоянные. Отсюда следует, что при выполнении условий леммы оr²s ^да и с помощью формулы Тейлора при любом фиксированном t получаем, что

p { Z N - k <  n - kr } P { ^ N <  n }

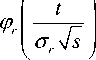
imr

or 4s

t

4 + m2

2o 2 s

t ² + 8 r ( X, t ) ,

где | d r ( X , t ) | <  C 5 E ( Z / r VOr²s ) ^3/2 . Используя (1), (5)(8) и формулу Стирлинга, нетрудно проверить, что при выполнении условий леммы s5 r ( X , t ) ^0 и из (9) находим, что sln ф_г (t /( o r s ^1/2 )) = im r st /( o r s ^1/2 ) - 1 ² /2 + о (1). Отсюда, из (4) и теоремы непрерывности следует утверждение леммы.

Лемма 5. Пусть s = N( 1- p)(1 + о (1))^да, (1- X ) N -^да. Тогда распределение суммы C_s ⁽ r ) / N ² слабо сходится к распределению вероятностей с плотностью (3).

Доказательство. Характеристическая функция случайной величины Z_s ⁽ r ⁾ / N ² имеет вид:

y ( r ) ( t ) = ( ф ( tIN² )- p r exp{ itr / N }) ^s (1- pr ) ^{- s} , где ф ( t ) - характеристическая функция случайной величины Z , . В лемме 3 доказано, что ф^N ( tN ² ) ^exp { y - ( Y ² -2 it ) ^1/2 } при любом фиксированном t . C помощью этого соотношения, формулы Тейлора и неравенства | e ix -1| < | x| находим, что

4 r ⁾( t ) =

( у - 4 у ² - 2 it ) s / N e

\ ₊ P r ⁽ У ^{-        2 )} ₊ O / 1 + rp r А

( 1 - P r ) N        I N^{2 J}

Учитывая (1) и формулу Стирлинга, нетрудно проверить, что rp r ^0 при r ^да, и, поскольку s = N ( 1- p) (1 + о (1)), получаем равенство y s ^{( r} ) ( t ) = = exp { y - ( Y ² -2 it ) ^1/2 + о (1)}. Из этого соотношения и теоремы непрерывности следует утверждение

леммы.

Докажем теорему 1. Пусть v = ( k - Np r )/( Np r ) лежит в любом конечном фиксированном интервале. При выполнении условия 1) с помощью (1) и формулы Стирлинга нетрудно проверить, что N - k = N (1- p r ) (1 + о (1)), и из лемм 3, 5 получаем

равенство

p { Z N - _k <  n - kr }

P { f N <  n }

( n - kr ) / N ²

J g (x) dx

-N^ ---------( 1 + о ( 1 ) ^{, (10)}

J g (x) dx

где ( n - kr )/ N = n / N + о (1), g ( x ) определено в (3). Следовательно,

p { Z N - k <  n - kr }

P{C < n}

Если выполнено одно из условий 2)-4) теоремы, то справедливы леммы 2 и 4, из которых получаем, что

xr

J e ^- x ^2/2 dx

1=-------- ( 1 + о (О) ,

J e ^{- x 2/2} dx

-=

где у = ( n - mN )/( oN ^1/2 ), x_r = ( n - kr - m_r ( N - k ))/( o_r ( N - k ) ^1/2 ). Используя (2), (5), несложно показать, что

у = ( n (1- X ) ^3/2 - N (1- X ) ^1/2 )/( XN) ^1/2 ,     (13)

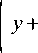
v ( m - r ) p"p _r АГ 1

^ C ^- p r ⁾ J^

x 1

vJpTkN

^{1 -} p r

( m - r ) ² p,

^{4 2} ( 1 ^- p_r )

- 1/ 2

-

- 1/2

x

Учитывая (1), (2) и формулу Стирлинга, получаем, что при выполнении одного из условий 2), 3) справедливы соотношения ( m - r ) ² p_r / о ² ^0 и x_r = у + о ( у + 1). Следовательно, x_r ^да при у ^да, а если | у I <  C , то x_r - у ^0. Отсюда и из (12) находим, что справедливо (11). Если выполнено условие 4), то с помощью (1), (2) нетрудно проверить, что x ₂ = ( у - v + о ( у + 1))/(6 X ) ^1/2 , и, поскольку у^да, легко видеть, что x ₂ ^да и из (12) следует (11).

Утверждение теоремы 1 получаем из леммы 1, соотношения (11) и приближения биномиальных вероятностей распределением Пуассона.

Докажем теорему 2. Пусть u = ( k - Np r )/( Np r (1- p_r )) ^1/2 лежит в конечном фиксированном интервале. Тогда N - k = N (1- p_r )(1 + о (1))^да и при выполнении одного из условий 1)-6) теоремы справедливы леммы 2, 4, из которых получаем (12), при этом, учитывая (5), несложно показать, что

xr

( У ⁺ u ( m ^- r ) д/ p r ( 1 ^- p r ) / ° | | l ^- p r )

/                                  2          \1/2 /                 /---------------------------\1/2 .

( i ^- p r ^- p r ( m ^- r ) / ° ² ) ( i ^- p r ^- V p r ( i ^- p r ) / N )

При X ^0, используя (1), (2), находим, что x 1 = ( у + о ( у + 1))/(1,5 X ) ^1/2 , x 2 = ( у + о ( у + 1))/(6 X ) ^1/2 , x r = у + о ( у + 1), r > 3. Отсюда и из (13) получаем, что при выполнении условия 1) теоремы x 1 , x ₂ ^да, а из (12) следует (11). Если выполнено условие 2), то x r ^да при у ^да и x r - у ^0, если |у | <  C . Из этих соотношений и (12) легко получить (11).

Также можно показать, что если справедливо одно из условий 3), 5), 6) теоремы, то p(m - r ) ² / о ² ^0 и x r = у + о ( у + 1), а если выполнено условие 4), то x r = ( у + O(u ( X -1 + r ^-1)) + о ( у ))х (1-(1- r + rX ) ² (1- X ) pX ^-1 (1- p_r ) ^-1 ) ^1/2 . С помощью этих соотношений, аналогично случаю X ^0, находим, что имеет место (11).

При выполнении условия 7) справедливы леммы 3, 5, из которых следует (10). С помощью (1)

для выбранных значений k нетрудно проверить, что ( n – kr )/ N ² = n / N ² + o (1), и из (10) получаем (11).

Если выполнено условие 8) теоремы, то y →–∞, y ³ / N ^1/2 →0, x_r = y (1 + O ( N ^–1/2 )) и, используя теорему 6.1.1 [1], получаем (12). Легко видеть, что x_r – y →0 и из (12) следует (11).

Утверждение теоремы получаем из леммы 1, соотношения (11) и асимптотики биномиальных вероятностей нормальным распределением.

Автор выражает благодарность профессору Ю. Л. Павлову за помощь в постановке задачи и обсуждении полученных результатов.

* Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант 13–01–00009.

LIMIT DISTRIBUTION OF GIVEN SIZE TREES’ NUMBER IN GALTON-WATSON FOREST WITH LIMITED NUMBER OF VERTICES