Предельные случаи релаксации, описываемые релаксационной функцией, полученной из колебательной модели релаксационной поляризации
Автор: Лукичв Александр Александрович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Научная жизнь
Статья в выпуске: 4-1 т.16, 2014 года.
Бесплатный доступ
В работе исследована релаксационная функция, полученная на основе колебательной модели недебаевской поляризации. Показано, что функция имеет два предельных случая, соответствующие различным видам поляризации. Быстрая поляризация ( t τ) линейна. Найдены границы для быстрой и медленной части релаксационной функции. Найден вид быстрой нелинейной и медленной нелинейной функций. Показано, что, вид поляризации определяется видом квазиупругой силы осциллятора. В общем случае релаксационную функцию можно представить в виде линейного и нелинейного слагаемых.
Короткий адрес: https://sciup.org/148203173
IDR: 148203173 | УДК: 537.226
Текст научной статьи Предельные случаи релаксации, описываемые релаксационной функцией, полученной из колебательной модели релаксационной поляризации
Попытки найти аналитические релаксационные функции с помощью обратного преобразования Фурье, соответствующие эмпирическим функциям КК, ДК и ГН оказались безуспешными.
Кольрауш, Вильямс и Ваттс [9] предложили эмпирическую релаксационную функцию:
(
P ( t ) = P g exp
к
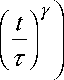
где Y — числовой коэффициент (1 < Y <0). Цифровое Фурье-преобразование от этой функции даёт спектры, близкие к распределениям ДК и ГН. Существуют и другие релаксационные функции, подобные функции (5), например, функция предложенная авторами работы [10], принципиальных отличий от (5) они не имеет.
Достаточно широко применяется термодинамический подход для объяснения релаксационной поляризации. Поскольку термодинамика по определению макроскопическая наука, то она в принципе не может объяснить микроскопические механизмы поляризации, но, в некоторых случаях, позволяет получить полезные соотношения. В работе [11] на основе кинетической теории получена следующая релаксационная функция:
^ q • t • uq ^ ф( t) = 1+-—0- т
к J
q
,
m 0 = k/m , k - коэфициент квазиупругой силы, m - масса осциллятора Y - коэффициент затухания, F ( t ) – внешняя вынуждающая сила. Это уравнение описывает заторможенный линейный осциллятор. Первое слагаемое обусловлено трением, второе – квазиупругой возвращающей силой.
Решение уравнения (7) без правой части даёт экспоненциальную релаксационную функцию, подобную функции (3). Очевидно, что Фурье-образ этой функции совпадает со спектральной формулой Дебая (1) с точностью до постоянного множителя. Отсюда был сделан вывод, что релаксационная поляризация это заторможенные колебания заряженных частиц [15, 16]. Поскольку функция Дебая не даёт точного совпадения с подавляющим большинством реальных релаксационных спектров, в работе [18] было сделано предположение, что для описания таких спектров может быть применена модель заторможенного нелинейного осциллятора, эта тема была продолжена в работе [19].
Рассмотрим частный случай колебаний осциллятора с нелинейной квазиупругой силой. В уравнении (7) представим квазиупругую силу в виде суммы линейного члена и нелинейной добавки:
здесь q – постоянная, зависящая от свойств материала, U 0 – константа, определяемая начальными условиями. Цифровое преобразование Фурье от (6) даёт растянутые частотные спектры с пиком поглощения, скошенным влево. В работах [12, 13], на основе термодинамического подхода, из других исходных посылок была получена релаксационная функция, подобная (6):
Известны, также и другие модели релаксационной поляризации, “прыжковая” модель, распределение времён релаксации [1, 2], парная модель [14] и другие. Но ни одна из них не даёт достаточно простых аналитических релаксационных или спектральных функций.
x xn f (x) = - + —, т Т1
здесь n – числовой коэффициент ( n і1). По аналогии вводим собственную частоту m 0 1 = k/m и постоянную времени т ^= Y / m 01 2 , соответствующие нелинейному слагаемому. Отношение постоянных времени т / т 1 показывает степень влияния нелинейной добавки на характер колебаний.
Уравнение заторможенного осциллятора (7) с нелинейной квазиупругой силой (8) примет вид:
1. РЕЛАКСАЦИОННАЯ ФУНКЦИЯ, ПОЛУЧЕННАЯ НА ОСНОВЕ КОЛЕБАТЕЛЬНОЙ МОДЕЛИ
В работах [15, 16] было показано, что спектральная формула Дебая (1) вытекает из решения уравнения линейного осциллятора. Если сила трения больше силы инерции осциллятора, в уравнении осциллятора можно пренебречь слагаемым, ответственным за инерцию. В этом случае мы получаем вырожденное уравнение для линейного осциллятора [17]
dx 1 1 F ( t )
— + - X + — x n = —^у. (9)
dt т т х m m 2
Это уравнение Бернулли, его решение известно [20]:
x ( t ) = I C • exp | ( n - 1) - I - — к к т J т х
s
= C n -1
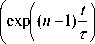
-
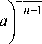
,(10)
здесь С – константа, определяемая начальными условиями, а = т / C• т 1 [19]. Нормировка функции (10) даёт:
^ ( t) =
dx 1 F ( t ) — + - x ==^-dt т m m 2 ’
1 [ 1 — a ] n - 1
expI (n -1) t I - a к т)
n - 1
. (11)
здесь х - координата осциллятора, т =2 Y / m 0 -постоянная времени, to 0 - собственная частота,
Таким образом, получена нелинейная релаксационная функция. Поскольку т и т 1 положительны, то для того, чтобы функция (11) была рацио-
нальной необходимо чтобы а< 1, или т 1 > т . Легко заметить, что при а= 0 функция (11) превращается в простую экспоненциальную функцию.
-
2. РАЗЛИЧНЫЕ РЕЖИМЫ ПОЛЯРИЗАЦИИ, ОПИСЫВАЕМЫЕ НЕЛИНЕЙНОЙ РЕЛАКСАЦИОННОЙ ФУНКЦИЕЙ
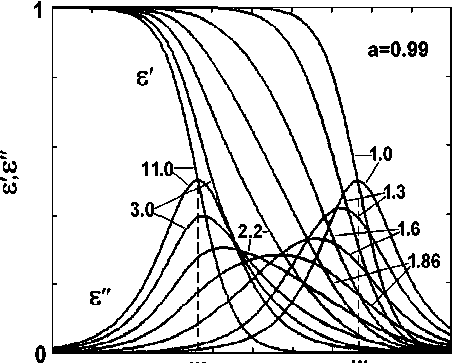
На рис. 1 [19] показаны частотные спектральные функции, полученные с помощью цифрового преобразования Фурье от функции (11). Преобразование Фурье не позволяет получить спектральную функцию в аналитическом виде.
Как видно из рис. 1, при n —— 1 и при n >10 cпектральная функция совпадает по форме с дебаевской [19]. В интервале 1< n <10 с ростом n происходит трансформация спектра, от дебаевского ( n = 1), до растянутого спектра с пиком поглощения, скошенным влево (1< n <1.9), далее до сильно растянутого с симметричным пиком ( n = 1.9), далее до растянутого спектра с пиком, скошенным вправо (1.9< n <10), и вновь до дебаевского спектра ( n >10). Наличие двух пиков в частотном спектре позволяет сделать предположение, что релаксационная функция (11) описывает два различных релаксационных процесса, при малых n ( n = 1), и при больших n ( n >10), при промежуточных значениях n , по всей видимости, имеется наложение этих двух процессов.
С математической точки зрения, линеаризацию спектра при n — 1 и при n >10 можно объяснить исходя из свойств уравнения (9). При n =1 уравнение (9) описывает линейный осциллятор с постоянной времени
* тт
т =---- т + Т1
То есть, при n —— 1 функция (11) асимптотически стремится к линейной функции (4) c постоянной времени т * . Линеаризацию спектра при n >10 можно объяснить следующим образом. Поскольку смещение заряженной частицы невелико ( x <<1), то при n >>1 в уравнении (9) член xn становится пренебрежимым по сравнению x . Уравнение (9) становится линейным и описывает колебания с характеристическим временем т , Также, если рассмотреть функцию (11), при n >10 и t~ т можно пренебречь параметром а , который будет мал по сравнению с экспонентой. При этом функция (11) трансформируется в простую экспоненциальную.
На рис. 2 показаны графики функции (11), по оси амплитуд использован логарифмический масштаб. График простой экспоненциальной функции вида (3) в таких координатах будет прямой линией. Сравним графики на рис. 1 и 2. Как видно из рисунка, при n =1 релаксационная фун-
w1 w2
W
Рис. 1. Спектральные функции, полученные с помощью цифрового преобразования Фурье от функции (11) для различных значений n при а =0.99.
Значения n указаны цифрами на графиках
кция линейна, этой функции соответствует дебаевский спектр (рис. 1). При n незначительно превышающем 1, график функции (11) становится нелинейным, спектр также отличается от дебаевского, пик поглощения имеет левую асимметрию.
При n =11 график релаксационной функции имеет протяженный линейный участок, приблизительно в пределах t =0,2- т - т . Очевидно, что в этом диапазоне функция (11) является простой экспонентой. Быстрая часть функции ( t <0,2^ т ) нелинейна. Очевидно, что при больших n функцию (11) можно представить в виде суммы линейной функции и незначительной нелинейной добавки. Спектральная функция при n >10 имеет дебаевскую форму, отсюда следует, что форма спектральной функции определяется только медленной частью релаксационной функции.
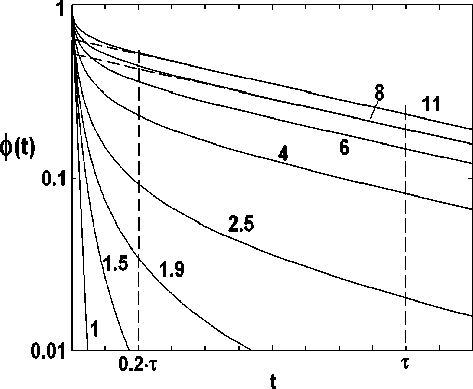
Рис. 2. Зависимость логарифмической амплитуды релаксационной функции (11) от времени для различных значений n .
Значения n указаны цифрами на графиках
Как следует из рис. 2 медленная часть функции заключена в диапазоне приблизительно 0,2^ Т < t < 2 т . Найдём более строгое условие, ограничивающее медленную часть функции (11). Слагаемым а можно пренебречь, если экспонента превышает это слагаемое по крайней мере в 10 раз, т.е. exp(( n -1)- t/ т )>10- a . Для а =0.99 и n =10 получаем t >0.26 т . Верхний предел интервала можно оценить, интегрируя функцию (11) в пределах от 0 до ^ , и от 0 до верхнего предела интервала. Интегрирование показывает, что значения интегралов отличается не более чем на 5% при верхнем пределе 3^ Т . Цифровое преобразование Фурье показывает, что различие в 5% не оказывает заметного влияния на форму спектра. Таким образом, медленная часть функции (11), определяющая форму частотного спектра находится в интервале 0,26 Т < t < 3- Т .
Из сказанного следует, что при малых n ( n >1) функция (11) является нелинейной, асимптотически стремящейся к линейной при n ^ 1. Найдём вид функции, совпадающей с (11) при малых значениях n . Как следует из рис. 2, функция (11) при малых n имеет заметную амплитуду только в области t <0.1- т . В этом случае справедливо условие t << Т , это позволяет экспоненту в функции (11) разложить в ряд в окрестности нуля:
^( t) =----1—f
[ 1 — a ] n - 1
( n - 1) - + 1
n - 1
a
^^^^^^~
, (13)
Т
Таким образом, мы можем представить функцию (11) в виде суммы линейной функции вида (3) и функции (13). Несложно заметить сходство функций (13) и (6). Графики функции (13) для различных n показаны на рис. 3, на рисунке использован логарифмический масштаб по времени. Там же для сравнения пунктиром показаны графики функции (11).
Рисунок показывает, что в интервале 1<‘ n <2 функции (11) и (13) совпадают практически полностью. Быстрые части функций (11) и (13) при t < Т 1 полностью совпадают для любого n . Сравнение графиков функции (13) со спектральной функцией (рис. 1) показывает, что функция (13) описывает спектры с левой асимметрией. В области t ~ т функция (13) даёт явно завышенные значения, поскольку разложение производилось в окрестности нуля. Из рисунка следует, что в интервале 1<п < 2 функция (13) с достаточной точностью совпадает с функцией (11).
-
3. ЗАКЛЮЧЕНИЕ
Таким образом, показано, что релаксационная функция (11) описывает различные режимы
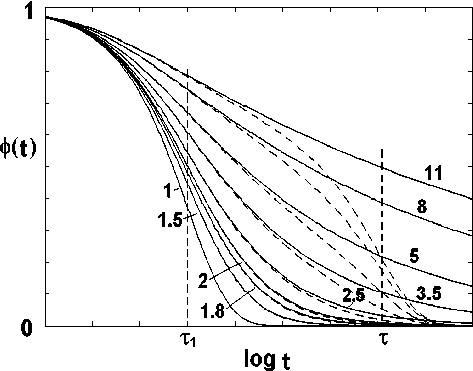
Рис. 3. Графики функции (13) в зависимости от логарифмического времени для различных значений n при а =0.99. Значения n показаны цифрами на графиках. Пунктиром построены графики функции (11) для тех же значений n и а
поляризации, при 1< n < 2 поляризация нелинейна, при 1< n < 2 релаксационный процесс представляет собой сумму линейного и нелинейного процессов, при n >10 поляризация линейна. Из рис. 1 следует, что частотные спектры можно разделить на два различных типа, по типу симметрии пика поглощения: с левой асимметрией и правой асимметрией. Для спектров с левой асимметрией преобладает нелинейный процесс, для правой асимметрии – линейный. В литературных источниках несложно найти экспериментальные спектры обоих типов. Из анализа доступных экспериментальных материалов можно сделать вывод, что для определённого материала наблюдается дисперсия только одного типа, либо с левой асимметрией, либо с правой. Материалы, показывающие при изменении внешних условий (температура, давление) спектры, с изменяющейся симметрией, обнаружить не удалось. Отсюда следует достаточно очевидный вывод, что вид колебаний заряженных частиц определяется структурой материала.
Как следует из сказанного, характер поляризации существенно зависит от параметра n . Это означает, что поляризация определяется видом квазиупругой силы, или формой потенциальной ямы, которая может быть найдена как интеграл от силы.
Проведённый выше анализ позволяет установить связь между колебательной моделью релаксационной поляризации изложенной в работах [19, 20], и термодинамической [12-14]. Термодинамическая модель описывает частный случай релаксационной поляризации, соответствующий малым значениям n для колебательной модели.
Список литературы Предельные случаи релаксации, описываемые релаксационной функцией, полученной из колебательной модели релаксационной поляризации
- Raju G.G. Dielectrics in electric fields. Marcel Dekker, New York, Basel. 2003.
- Поплавко Ю.М. Физика диэлектриков. Киев: Вища школа, 1980.
- Yu. Feldman, A. Puzenko, Ya. Ryabov, in: Advances in Chemical Physics, 133, Part A, Fractals, diffusion and relaxation in disordered complex systems, Ed. Yu. P. Kalmykov, Wiley&Sons, 2006. P. 1-125.
- Дебай П. Полярные молекулы: пер. с нем. М.-Л.: ГНТИ, 1931.
- Cole K.S., Cole R.H. Dispersion and absorption in dielectrics. J. Phys. Chem. v. 9, 1941. pp. 341-351.
- Davidson D.W., Cole R.H. Dielectric relaxation in glycerol, propylene glycol and n-propanol. J. Chem. Physics, v. 19, 1951. pp. 1484-1490
- Havriliak, S. Negami S. A complex plane analysis of a-dispersion in some polymer systems. J. Polym. sci. C, v. 14, 1966. pp. 99-117.
- Губкин А.Н.//Изв. ВУЗов, Физика, 1979, № 1. C. 56-73.
- Williams, G., Watts, D.C. Non symmetrical dielectric relaxation behavior arising from a simple empirical decay function//Trans. of the Faraday Soc. v. 66, 1970. pp. 80-85.
- Govindaraj G., Murugaraj R. A new amomalous relaxation function and electrical properties of disordered materials//Material Science and engineering, v. B77, 2000. pp. 60-66.
- Zon B.A. Nonlinear model of non-Debye relaxation//arXiv: 1003.3917v. 8 p.
- Tsallis C. Anomalus distribution, non-linear dynamics, and nonextensivity//Physica D, v. 193, 2004. pp. 3-34.
- Brouers F., Sotolongo-Costa O., Weron K. Burr, Levy, Tsallis//Physica A, v. 344, 2004. pp. 409-416.
- Ngai K.L. A schematic description of the dynamics of glass transition by the coupling model. in S.J. Rzoska, V.P. Zhelezny (eds.) Nonlinear dielectric phenomena in complex liquids, Kluwer academic Publishers, Netherlands, 2004. p. 247-258.
- Костюков Н.С., Лукичёв А.А. Связь гармонических функций с формулами Дебая для частотной зависимости//Электричество. 2002, № 1. с. 55-58.
- Лукичёв А.А., Ильина В.В. О возможности построения единой модели резонансной и релаксационной поляризации//Электронный журнал "Исследовано в России", 171, 2005. C. 1778-1792. http://zhurnal.ape.relarn.ru/articles/2005/171.pdf
- Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Наука, 1991. 568 с.
- Лукичёв А.А. Моделирование спектральных функций осциллятора с кубической нелинейностью возвращающей силы.//Известия Самарского научного центра РАН, т. 11, 2009, № 5. с. 46-48.
- Lukichev A.A. Relaxation function for the non-Debye relaxation spectra description//Chemical Physics, 2014, v. 428. pp. 29-33.
- Зайцев В.Ф., Полянин А.Д. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 2001.


