Предельные теоремы для случайных матриц
Автор: Тихомиров А.Н.
Журнал: Известия Коми научного центра УрО РАН @izvestia-komisc
Рубрика: Физико-математические науки
Статья в выпуске: 3, 2010 года.
Бесплатный доступ
Приводится обзор результатов по предельным теоремам для случайных матриц, полученных за последние 10 лет в совместных исследованиях А.Н. Тихомирова и немецкого математика профессора Ф. Гётце. Рассматриваются скорость сходимости к полукруговому закону, скорость сходимости к распределению Марченко- Пастура, метод СтеЙва для случайных матриц, доказательство кругового закона и предельные теоремы для степеней и произведений случайных матриц.
Случайные матрицы, полукруговой закон, вигнеровские матрицы
Короткий адрес: https://sciup.org/14992401
IDR: 14992401 | УДК: 519,2
Текст научной статьи Предельные теоремы для случайных матриц
Теория случайных матриц – активно развивающаяся в последние десятилетия область математики. В начале 50-х гг. прошлого столетия Вигнер предложил использовать матрицы большой размерности, элементы которых суть гауссовские случайные величины, для описания дискретной части спектра гамильтониана взаимодействия элементарных частиц тяжелых атомов. Это дало толчок к развитию теории случайных матриц, нашедшей широкое применение в различных областях знаний. Значительный прогресс в изучении асимптотики поведения спектра случайных матриц был достигнут буквально в последние годы. В настоящей статье мы попытаемся отразить некоторые результаты, полученные автором совместно с Ф. Гётце (F. Götze, Германия), С. Г. Бобковым (Миннесота, США) и учениками Н. Алексеевым и Д. Тимушевым, рассмотрим вигнеров-ские ансамбли, т.е. совокупность эрмитовых матриц с независимыми (с точностью до симметрии) элементами, и ансамбли выборочных ковариационных матриц. Будут приведены также результаты о поведении спектра неэрмитовых матриц с независимыми элементами. Нас будет интересовать асимптотическое поведение прореженных матриц, возникающих, например, в задачах описания цензурированных статистических данных большой размерности. Также мы рассмотрим одно из новых направлений в теории случайных матриц – изучение сингулярного спектра степеней и произведений случайных матриц с независимыми элементами (без предположений симметрии) и собственного спектра произведения случайных матриц.
1. Вигнеровские случайные матрицы
В 1955 г. Вигнер в работе [1] доказал, что математическое ожидание эмпирического распределения, определенного на множестве собственных чисел симметричной случайной матрицы, элементы которой независимые (с точностью до симметрии) случайные величины, принимающие значения +1 или -1 с вероятностью 1/2, сходится при неограниченном росте размерности матрицы к распределению с плотностью, график которого представляет полуокружность радиуса 2. Этот результат получил в дальнейшем название полукругового закона, а соответствующее распределение называют полукруговым распределением. Полукруговой закон был распространен на очень широкие классы случайных матриц. Так, уже в 1958 г. Вигнер в работе [2] доказал полукруговой закон для симметричных случайных матриц с субгауссовскими элементами (случайная величина £ называется субгауссовской, если существует такая положительная постоянная р > 0, что для любого x > 0 Pr{|С| > x} 6 exp{-px2}). Гренандер (см., например, Гирко [3]) показал, что эмпирическое спектральное распределение случайной матрицы (равномерное распределение на множестве собствен- ных чисел матрицы) сходится по вероятности с ростом размерности матрицы к полукруговому распределению. Арнольд в работе [4] доказал сходимость почти наверное эмпирической спектральной функции распределения симметричной случайной матрицы к полукруговому распределению. Окончательно было показано, что слабый полукруговой закон (сходимость по вероятности эмпирической спектральной функции распределения к полукруговому распределению) имеет место, если элементы матрицы независимы, имеют одинаковые математические ожидания и дисперсии и удовлетворяют условию Линде-берга (см., например, Гирко [3]).
Приведем формальное описание упомянутых выше результатов. Пусть ξ jk , 1 6 j 6 k треугольный массив независимых случайных величин (вещественных при j = к и, возможно, комплексных при j < к ) с E j = а и дисперсией E I j - a| 2 = ст 2 , где a – произвольное комплексное число, а σ – произвольное положительное число. Рассмотрим последовательность матриц
( X 11 X 12 ■■■ X 1 n- 1 X 1 n \
X 21 X 22 ••• X 2 n- 1 X 2 n j
,
··· ··· ··· ···
Xn 1 Xn2 ••• Xnn-1 Xnn/ где Xjk = j и Xkj = j для 1 6 j 6 к. Заметим, что матрицы X(n) обладают свойством эрмито-вости (они симметричны, если все элементы вещественны или эрмитово сопряженные, если элементы комплексные, т. е. X(n) = X(n), где X(n) означает транспонированную и комплексно сопряженную матрицу X(n) ). Собственные числа таких матриц вещественны и мы обозначим их в порядке возрастания: а1n) 6 ■ ■■ 6 АПп). Определим эмпирическую спектральную меру матрицы X(n), приписав каждому значению Аjn) вероятность 1 /п и соответствующую этой мере эмпирическую спектральную функцию распределения
1 n
F n ( x ) = п Е I {A j < x},
П j =1
где I {A} означает индикатор события A . Символом F n ( x ) обозначим математическое ожидание функции F n ( x ) , F n ( x ) = E F n ( x ) . Пусть G ( x ) -функция распределения полукругового закона с параметром ст = 1 , т.е. функция распределения с плотностью
g ( x ) = G ( x ) = E V4 — x 2 I {|x | 6 2 }.
2 n
Определение 1. Будем говорить, что к последовательности случайных матриц X ( n ) применим
-
• полукруговой закон Вигнера , если
lim n^^ F n ( x ) = G ( x ) ,
-
• слабый полукруговой закон , если
plim n^^ F n ( x ) = G ( x ) (сходится по вероятности) ,
-
• усиленный полукруговой закон , если
Plim n^^ F n ( x ) = G ( x ) (сходится почти наверное) .
Заметим, что усиленный полукруговой закон влечет за собой слабый полукруговой закон, а из слабого полукругового закона следует, в свою очередь, полукруговой закон Вигнера. Мы приведем основной результат о применимости полукругового закона к случайным матрицам.
Теорема 1. Пусть случайные величины j, 1 6 j 6 k независимы, имеют одинаковые математические ожидания E j = а и одинаковые дисперсии E Ij - al2 = ст2 для некоторого ст > о. Предположим, что случайные величины ξjk удовлетворяют условию Линдеберга nn
L n ( т ):=^nE Е x 2 dF jk ( x ) ^ 0 ,
п(п +1) j=1k=j_ >тvn} J когда n → ∞, где Fjk (x) = Pr {j I < x}. Тогда последовательность матриц X(n) удовлетворяет слабому полу-круговому закону.
Этот результат был впервые получен Пасту-ром в работе [5]. Гирко (см. [3]) при близких предположениях доказал усиленный полукруговой закон. Теорема 2. Пусть случайные величины ^ jk , 1 6 j 6 k независимы, имеют одинаковые математические ожидания E ^ jk = а и одинаковые дисперсии E l j — al 2 = ст 2 для некоторого ст > о . Предположим, что случайные величины ξ jk удовлетворяют модифицированному условию Линдеберга
1n 2
1уn (т) := — max j x2dFjk (x) ^ 0, когда n → ∞, где Fjk (x) = Pr {j I < x}. Тогда последовательность матриц X(n) удовлетворяет усиленному по-лукруговому закону.
Не умаляя общности, мы будем считать в дальнейшем, что ст 2 = 1 . Скорость сходимости в полукруговом законе одним из первых начал изучать Гирко (см. [3]). Основной метод исследования скорости сходимости в полукруговом законе, предложенный им, – это использование преобразования Стилтьеса. Надо заметить, что данное преобразование в теории случайных матриц впервые использовали Марченко и Пастур в 1967 г. [6] для доказательства сходимости эмпирической спектральной функции распределения некоторых случайных операторов. Гирко была найдена одна из первых оценок расстояния по Колмогорову между функциями распределения через их преобразование Стилтьеса. В 1993 г. Бай [7] улучшил результат Гирко, получив более точную оценку расстояния по Колмогорову между функциями распределения через преобразования Стилтьеса и, благодаря этому, более точную оценку скорости сходимости. В качестве меры скорости сходимости в полукруговом законе Вигнера мы введем расстояние по Колмогорову между математическим ожиданием эмпирической функции распределения и функцией распределения полукругового закона
-
△ n := sup lF n ( x ) - G ( x ) |. x
В 2002 г. независимо были получены оценки вида △ n = O ( n - 1 / 2 ) одновременно в трех работах: Гир-ко [8], Бай и соавторы [9], Гётце и Тихомиров [10]. Во
всех работах использовались разные подходы. Следует отметить, что оценка, полученная в работе Гёт-це и Тихомирова [10], давала более точную зависимость от моментов распределения случайных матриц. Кроме того, Гётце и Тихомировым была получена оценка скорости сходимости в слабом полукру-говом законе лучше по порядку зависимости от n , чем в работе Бая и соавторов. Гирко не рассматривал скорость сходимости в слабом полукруговом законе. Также в работе [10] было получено более точное неравенство для оценки расстояния по Колмогорову между функциями распределения через их преобразования Стилтьеса. Ниже мы приведем эти результаты более детально. В качестве меры скорости сходимости в слабом полукруговом законе рассмотрим величину
Д n := E sup IF n ( x ) - G ( x ) |.
x
Очевидно, что Д n 6 Д n . Мы приведем сначала неравенство, позволяющее оценивать близость между функциями распределения через их преобразования Стилтьеса. Дадим определение преобразования Стилтьеса.
Определение 2. Для любой случайной величины ξ с функцией распределения G ( x ) определим преобразование Стилтьеса равенством
S G ( ^ )= E 1М
∞
= L dG ( x ' •
где z = u + V— 1 v , v > 0 .
Определим для любых функций распределения F и G расстояние Леви как
L ( F, G ) = inf {5 > 0 : F ( x — 8 ) — 8 6 G ( x )
6 F ( x + 8 ) + 8, Vx € R }. (1)
В работе Бобкова, Гётце и Тихомирова [11] доказано следующее неравенство.
Теорема 3. Пусть F и G произвольные функции распределения. Существует такая универсальная постоянная c> 0, что для любых 0 < v0 < v1 выполнено cL(F, G) 6 vо + vо supIm(Sg(x + V—1 vo))
x
+
∞
∞
IS f ( u + V— 1 v ) — S g ( u + V— 1 v ) | du
+ sup xE [a +2vо ,в — 2vо]
v 1
( S F ( u + V— 1 v )
v 0
— Sg (u + V 1 v)) dv где a < в выбраны так, чтобы G (a) 6 v0 и G (в) > 1 — v 0.
В частности, в случае, если G распределение полукругового закона, то теорема 3 влечет следующий результат.
Теорема 4. Если G функция распределения стандартного полукругового закона, F – функция распределения, то существует такая универсальная постоянная c > 0, что для любых vi > v0 > 0 выпол- нено csup IF(x) — G(x)|
x
6 sup
XE [ - 2 , 2]
v 1
( Sf (x + V—1 v) — Sg (x + V—1 v)) dv v0
+ / IS F ( u + V— 1 v i ) — S g ( u + V— 1 v i ) Idu + v о .
-∞
Последнее неравенство было доказано в работе Гётце и Тихомирова [10]. С применением теоремы 4 получен целый ряд оценок скорости сходимости в полукруговом законе Вигнера и слабом полукруго-вом законе.
Теорема 5. Пусть случайные величины j , 1 6 j 6 k независимы и имеют нулевые математические ожидания и единичные дисперсии
E j =0 U E j 1 2 = 1 .
Кроме того, предположим, что выполнено условие sup E I^ jk 1 4 =: M 4 < ro.
1 6 j 6 k
Тогда найдется такая универсальная постоянная
C > 0 , что
Д n 6 CM 4 2 n - 2 . (2)
Если дополнительно предположить, что sup E Ij12 =: M12 < ro, i6j6k то найдется такая универсальная постоянная C > 0, что
Д * 6 CM 69 n - 2 . n 12
Преимущество оценки (2) состоит в том, например, что из нее непосредственно вытекает оценка скорости сходимости в полукруговом законе Вигнера для прореженных (sparse) матриц. В частности, мы имеем следующий результат. Пусть е jnk ) 1 6 j 6 k 6 n последовательность треугольных массивов, независимых при каждом фиксированном n , бернул-лиевских случайных величин (принимающих значения либо 0 , либо 1 ) с E е jn ) = p n с некоторым параметром 0 < p n 6 1 . Относительно случайных величин е jn \ 1 6 j 6 k 6 n предположим также, что они не зависят от совокупности случайных величин ξ jk , 1 6 j 6 k . Определим прореженные матрицы как эрмитовы матрицы
-
( 6 ) v( е ) v( е ) v( е
/ X 11 X 12 ■■■ X 1 n- 1 X 1 n
, , 1 V( е ) v( е ) v( е ) v( е )
х ( е ) = X 21 X 22 • • • X 2 n- 1 X 2 n ,
VnPn ............ ’
( e ) V)e ) V)e ) V)e
\ Xn 1 X n 2 ••• X nn- 1 X nn )
( ^ ) -( n ) V( ^ ) V"( ^ )
где X jk = £ jk ^ jk и X kj = X jk для 1 6 j 6 k . Чтобы не загромождать обозначения, мы не отразили зависимость от n в обозначениях случайной величины X ( ! ) . Обозначим A ( e ) 6 • • • 6 А Пе ) собственные числа jk 1
матрицы X ( e ) и определим эмпирическую спектральную функцию распределения матрицы Х ( е )
n
Fn6)(x ) = 1 V I {A (6) Математическое ожидание эмпирической спектральной функции распределения прореженной матрицы обозначим Fnе) (x) = E FnE)(x). Положим An) := supx\FnE)(x) - G(x) |. Оценки скорости сходимости в полукруговом законе Вигнера для таких матриц дает следующая теорема. Теорема 6. Пусть случайные величины j, 1 6 j 6 k независимы и имеют нулевые математические ожидания и единичные дисперсии E j =0 U E j 12= 1. Предположим, что npn → ∞, когда n → ∞. Кроме того, предположим, что выполнено условие sup E I^jk 14 =: M4 < ro. 16 j 6 k Тогда найдется такая универсальная постоянная C > 0, что △n) 6 CM42(npn) - 2. Доказательство теорем 5 и 6 приведено в работе [10], а оценки скорости сходимости при более слабых ограничениях на моменты элементов матрицы получены в статье [12]. Теорема 7. Пусть случайные величины j, 1 6 j 6 k независимы и имеют нулевые математические ожидания и единичные дисперсии E j =0 и E j 12= 1. Кроме того, предположим, что выполнено условие sup E j 12+5 6 M2+5 < ro j,k для некоторого 8 e (0,2 . Тогда 2δ △n 6 cm,:j n-2+. Оценки, приведенные в теоремах 5–7, являются наилучшими из известных, но вопрос об их оптимальности остается открытым. Для некоторых классов распределений элементов матрицы X удается получить лучшие по порядку зависимости отn оценки скорости сходимости в полукруговом законе Вигнера, а также в слабом полукруговом законе. Приведем следующие определения для гауссовских ансамблей. Определение 3. Пусть элементы эрмитовой (или вещественной симметричной) матрицы независимы (с точностью до симметрии) и имеют гауссовское распределение с нулевым средним, при этом диагональные элементы имеют дисперсию 2ст2, а внедиагональные - ст2. Тогда говорят, что матрица принадлежит гауссовскому унитарному (ортогональному) ансамблю GUE (gOe) с ст2= 1. Для случайных матриц из гауссовских ансамблей удается получить оптимальные оценки скорости сходимости в полукруговом законе Вигнера. Теорема 8. Пусть случайная матрица X принадлежит GUE (GOE). Тогда существует такая постоянная C > 0, что △ n 6 C Случай гауссовского унитарного ансамбля был рассмотрен в работе Гётце и Тихомирова [13], а случай гауссовского ортогонального ансамбля – в работе Тимушева, Тихомирова, Холопова [14]. Оценку скорости сходимости в полукруговом законе Вигнера лучше по порядку зависимости от размерности матрицы, чем O(п-2) удается получить не только для случайных матриц из гауссовских ансамблей. Так, например, оценку удается улучшить для матриц, распределение элементов которой имеет невырожденную гауссовскую компоненту. Теорема 9. Пусть j = njk + aZjk, где a > 0, а случайные величины njk, 1 6 j 6 k независимы в совокупности и не зависят от случайных величин Zjk. Случайные величины Zjk, 1 6 j 6 k — независимые в совокупности гауссовские величины с нулевым средним, причем, если j < k, то ζjk – комплексные с независимыми вещественной и мнимой частью с дисперсией равной 1, если j = k, то Zjk суть вещественные гауссовские величины с нулевым средним и дисперсией равной 2. Пусть sup E Ij Ip 6 Mp < ro для любого p > 1. j,k Тогда для любого v > 0 найдется такая постоянная C(a, v), зависящая лишь от а и v, что △n 6 C(a, v)п-3 + v. Этот результат был получен в совместной работе Гётце, Тимушева и Тихомирова [15]. Улучшить оценку скорости сходимости в полукруговом законе Вигнера и слабом полукруговом законе удается еще для одного класса распределений. Определение 4. Говорят, что вероятностная мера µ на Rd удовлетворяет неравенству типа Пуанкаре с константой ст2, если для любой ограниченной гладкой функции наRd с градиентом ∇g, выполнено нера- венство Var (g) 6 ст2 j I^gI2d^. Теорема 10. Пусть случайные величины ξjkодинаково распределены и их распределение удовлетворяет неравенству типа Пуанкаре на вещественной прямой. Тогда найдется такая постоянная C, что △ n 6 Cn-3 и △ n 6 Cn3log2(n + 1) . Последний результат был получен в совместной работе Бобкова, Гётце и Тихомирова [11]. В этом параграфе мы будем предполагать, что задан двумерный массив независимых случайных величин ^jk, 1 6 j,k, с E ^jk = 0 и E Ij 12= ст2. Величины ^jk могут быть комплексными. Пусть n,p > 1. Рассмотрим прямоугольную матрицу n × p X11 X12 • • • X21 X22 • • • . Xn 1 Xn 2 • • • X1p-1 X1p X2p-1 X2p ··· ··· Xnp-1 Xnp где Xjk = j для всех 1 6 j 6 n и для всех 1 6 к 6 p. Определим выборочную ковариационную p × p матрицу равенством W = X * X. Впервые такие матрицы рассмотрел для гауссовских величин Уишарт (Wishart) в 1928 г. в работе [16]. Он нашел совместное распределение элементов матрицы W в случае, когда случайные величины ξjk гауссовские. Это распределение впоследствии стало называться распределением Уишарта, а матрицы иногда тоже называют матрицами Уишарта. Поскольку матрица W неотрицательно определена, ее собственные числа неотрицательны. Обозначим их в порядке убывания 0 6 sр 6 ■■■ 6 s 1 и определим эмпирическую спектральную меру, приписав каждому собственному значению вероятность 1 /n. Определим также эмпирическую спектральную функцию распределения матрицы W равенством p F„,p(x) = p Z?{sj Математическое ожидание эмпирической спектральной функции распределения обозначим F„,p(x) = EFn,p(x). При изучении асимптотики спектральных функций распределения матрицы W представляет особый интерес случай, когда p меняется в зависимости от n, причем так, что, например, существует предел y = lim„ ^ „. В 1967 г. Марченко и Пастур в работе [6] в предположении, что случайные величины j имеют 4-й момент, показали, что распределение F„,p(x) сходится к распределению Gy (x), которое имеет плотность dGy(x) = 5(x)(1 - y)+ + -±- V(x — a)(b — x), dx 2Пyx где 5(x) - дельта-функция Дирака, a = (1 - Vy)2, b = (1 + Vy)2. Здесь мы использовали обозначение a + = max {a, 0}. Распределение Gy (x) называют распределением Марченко-Пастура с параметром y. Заметим, что распределение Марченко-Пастура имеет скачок в 0 величиной 1 - y при 0 6 y 6 1. Поскольку ненулевые собственные числа матриц X∗X и XX∗ совпадают, не умаляя общности, мы можем считать, что y > 1. Имеет место следующая теорема. Теорема 11. Пусть семейства случайных величин j 1 6 j 6 n, 1 6 к 6 p (j = ^(к)) независимы при каждом фиксированном n , имеют нулевое математическое ожидание и единичную дисперсию. Предположим далее, что p = p(n) меняется с ростом n так, что lim„^^ „ = y и случайные величины удовлетворяют условию Линдеберга, т. е. для любого т> 0 выполнено следующее: L„ (т) Тогда np П^ЕЕEj12I {j1> т Vn} ^0• n j=1 к=1 sup |F„p(x) — Gy (x) | ^ 0, когда n ^ x. x Более того, функция распределения F„p (x) сходится к распределению Марченко-Пастура Gy (x) по вероятности. Доказательство этого результата можно найти, например, в работе Бая [17]. Скорость сходимости спектральной функции распределения к распределению Марченко-Пастура изучалась несколькими авторами. Так, один из первых результатов получен Баем в 1993 г. [18] и позднее уточнялся им же с соавторами. В 2003 г. независимо Баем и соавторами [19] и Гётце и Тихомировым [20] была получена оценка скорости сходимости вида Д „р = supx\F„p(x) — Gy(x) | = O(n- 2) в предположении конечности восьмого момента у элементов матрицы X. Скорость сходимости по вероятности Д „р = E supx\F„,p(x) — Gy(x) | = O(n-2) в упомянутой работе Гётце и Тихомирова [20] доказана в предположении конечности 12 моментов у элементов матрицы X. Эти оценки улучшены и дополнены в работе Гётце и Тихомирова [21] и работе Тихомирова [22]. Окончательно можно сформулировать следующий результат. Теорема 12. Пусть семейства случайных величин j 1 6 j 6 n, 1 6 k 6 p (j = ^jk)) независимы при каждом фиксированном n, имеют нулевое математическое ожидание и единичную дисперсию. Предположим далее, что p = p(n) меняется с ростом n так, что „ = y > 1. Пусть для некоторого 0 <5 6 2 M2+5 := sup E lj l2+5< х. j,k,n Тогда найдется такая постоянная C = C (5), зависящая от δ, что δδ д„р 6 cm2++5n-2+ • Результат для 5 = 2 получен в работе Гётце и Тихомирова [21], общий случай (0 < 5 < 2) рассмотрен в работе Тихомирова [22]. Приведенные оценки являются наилучшими из известных, но вопрос об их оптимальности, также как и в случае полукруго-вого закона, остается открытым. Лишь для гауссовских матриц удается получить оптимальные оценки скорости сходимости вида Д„р = O(n-х) и то, пока известна эта оценка лишь для матриц из так называемого унитарного ансамбля Лагерра, т.е. для таких матриц, элементы которых комплексные нормально распределенные случайные величины с независимыми и одинаково распределенными вещественной и мнимой частью, см. работу Гётце и Тихомирова [13]. В этом параграфе мы приведем дифференциальные уравнения, характеризующие полукруговой закон рапределения и распределение Марченко-Пастура. На основе этих уравнений разработан метод, позволяющий доказывать сходимость к соответствующему распределению не только для матриц с независимыми элементами, но и с элементами, удовлетворяющими некоторым условиям зависимости. Пусть C(R) (соответственно Cx(B), B с R) означает класс непрерывных функций на вещественной прямой R (соответственно, класс дифференцируемых функция на B, с ограниченной первой производной на любом компактном подмножестве B). Вве- дем в рассмотрение класс функций • для любого т> 0 C{-2,2} := {f : R ^ R : f G C \ {-2, 2}; limsup lyf (y)| < го; limsup |4 - y2||f‘(y)| < C}. |y|^^ y^± 2 Теперь мы можем сформулировать одно из основных утверждений данного параграфа. Утверждение 1. Случайная величина ξ имеет функцию распределения полукругового закона G (x) с плотностью g(x) = G‘(x) = 2ПV4 - x2i{x| 6 2} тогда и только тогда, когда для любой функции f g C{_2 2} выполнено равенство E (4 - 5 2) f ‘ (x) - 3E 5f (5 )=0. 3.1. Уравнение Стейна для случайных матриц Пусть W означает симметричную случайную матрицу с собственными значениями A1 6 • •• 6 An. Если W = U- 1AU, где U - ортогональная матрица и Λ – диагональная матрица, то по определению f (W) = U -1 f (Л)U, где f (Л) = diag (f (A1),..., f (An)). Теорема 13. Пусть дана последовательность случайных матриц Wn размерности n × n таких, что для любой функции f G C{-2,2} n- 1E (4In - Wn) f ‘(W - n) - 3n- 1E Tr Wnf (Wn) ^ 0, когда n → ∞. Тогда выполнен полукруговой закон Вигнера, т. е. △n := sup Fn(x) - G(x)| ^ 0, когда n ^ ro. x Полукруговой закон Вигнера для случайных матриц с мартингальной структурой зависимости элементов. Пусть дан треугольный массив случайных величин ξjk, 1 6 j 6 k, имеющих нулевые средние E 5jk = 0 и конечные дисперсии E I5jk|2= ^2k. Для любых 1 6 j 6 k 6 n введем ст-алгебры F(jk) = CT{^iq, 1 6 l 6 q 6 n, (lq) = (jk)}, и F(j) = a{^lq, 1 6 l 6 q 6 n, (l) = (j)}. Введем также в рассмотрение дробь Линдеберга для случайных матриц, определив ее равенством Ln (Т) = A EE E j 12I {j \ > TVn}, T > 0. Tl j=1 k = j Определим усеченные случайные величины 5(k) = 5jk I {j 1 > TVn}- E 5jk I {I5jk I > TVn}, (^jkУ = E (5jT))2. (3) Мы сформулируем основную теорему этого параграфа. Теорема 14. Предположим, что случайные величины ^jk, 1 6 j 6 k удовлетворяют следующим условиям: • для любого T > 0 e {5jTk) IF(jk)} = 0; • существует C < ∞, такая что max max — > ст „7 6 C; 16n<^ 16j6n n j nn e n1 := A EE E |e {(533T ))2|F( j)} - (азT ))2| ^ 0, n2 j j j=1 k=1 при n ^ го; • для любого T > 0 n e(2):= E E E E {((^(T))2 - E (^(T))2) n n3 2-^ | pvsjk ’ jkjk ’ ’ j=116k=16 n X ((5 (T ))2- E (^ (T ))2) I F(j )}E 0, при n ^ro; (5) jj • существует a > 0 такое, что nj=1 k=1 • для любого фиксированного t > 0 Ln (т) ^ 0, при n ^ го. Тогда △n = sup I Fn (xct) - G (x) I ^ 0. x 3.2. Метод Стейна для выборочных ковариационных матриц Доказательство утверждений, приведенных в этом параграфе, можно найти в статье Гётце и Тихомирова [23]. В настоящем параграфе мы приведем уравнения, аналогичные изложенным в предыдущем параграфе, характеризующие распределение Марчен-ко-Пастура. Пусть gy (x) и Gy (x) обозначают соответственно плотность и функцию распределения Мар-ченко-Пастура с параметром y. Введем в рассмотрение, как и ранее, класс функций C{a,b} = {f : R ^ R,f G C1(R \{«,b}); lim sup xf (x) < го, |x|→∞ limsup I(x - a)(b - x)|2 | f ‘(x)| < ro}. (6) x→b+2a±b-2a Следующее утверждение содержит характеризацию распределения Марченко-Пастура с помощью дифференциального уравнения типа Стейна. Утверждение 2. Случайная величина ξ имеет распределение Марченко-Пастура с параметром y тогда и только тогда, когда для любой функции f ∈C{a Ь} выполнено следующее равенство: E (5 - a)(b - 5)5f ‘(5) - 3E 5(5 - a+b) f (5) = 0. Рассмотрим теперь выборочную ковариационную матрицу W = X*X с собственными числами s2 > ••• > sn. Критерий сходимости математического ожидания спектральной функции распределения матрицы W к распределению Марченко-Пастура дает следующая теорема. Теорема 15. Пусть последовательность случайных матриц W такова, что для любой функции f ∈ C{a b, выполнено следующее: 4. Круговой закон n-1E Tr(W n - a In)(bIn - Wn )W nf ‘ (Wn) - 3n- 1E Tr Wn (Wn - a+b In) f (Wn) ^ 0, когда n → ∞. (7) Тогда Дn = sup iFn(x) - Gy (x)I ^ 0, x где y = a+b - 1. Опираясь на этот критерий можно доказать следующую теорему. Теорема 16. Пусть p = p(n) зависит от n так, что y = n G (0, 1]. Предположим, что случайные величины fjk, 1 6 j 6 n, 1 6 k 6 p удовлетворяют следующим условиям: • для любого т > 0 e {fjk’ IF(jk’} = 0; • существует такая C < ∞, что Пусть Xij, 1 6 i 6 n, 1 6 j 6 n, совокупность таких независимых случайных величин, что EXij = 0 и EXij = 1. Определим матрицу X = X11 1 X 21 X12 X 22 n \ Xn 1 Xn 2 X1n X 2 n . . . Xnn Обозначим A 1, ...,An собственные числа мат- 1n max max — \ 16n<^ 16j6n n "ji 6 C; рицы X и определим ее эмпирическую спектральную функцию распределения Fn(x,y) = n En=11{ReAk 6 x, Im Ak 6 y1. Будем говорить, что для матрицы X выполнен круговой закон, если ожидаемая спектральная функция распределения E Fn(x,y) сходится при n ^ го к функции равномерного распределения в единичном круге F (x, y), т.е. к функции распределения с плотностью f (x, у) = ПI{x2+ у26 1}(x,y). Описанные ансамбли случайных матриц впервые были введены в работе Жи-нибра (Ginibre) [38]. Им получены совместные распределения для собственных чисел A 1,..., An в слу- • для любого т > 0 np £“’ := EE E^ <(fj" j’ 1- ("j"’Ф 0, j=1k=1 при n ^ ro; • для любого т > 0 n «n2’ :=n E E E^ {«fjTV j=116k=16 p (TЛ2,иУС(t Л2 T? (TЛ2№(j ’ } I 0 -E (fjk ) )((fji ) - E (fjk ) )F | ^ 0, при n ^ ro; чае когда Xjk независимые гауссовские величины. Впоследствии соответствующие матрицы получили название ансамблей Жинибра. Мета (Mehta) в 1967 г. [25], опираясь на работу Жинибра показал, что для матриц из ансамбля Жинибра, элементы ко- и n «: = j E E E^ {«jk’)2 j=116k=16 p E (т)(T’^Шт/T’'I2 - E t’323IIF(j’} I 0 E (njk ) )((njl ) E (njk ) )IF J£ 0, при n → ∞, где 4njT’ := E (fjT’ IF(jk’); • существует такое " > 0, что £ n4) := n2^ j-" - "2 | ^ 0, при n .; nj=1 k=1 • для любого фиксированного т > 0 Ln (т) ^ 0, при n ^ го. Тогда Дn = sup Fn (x") - Gy (x"- 1) | ^ 0. x Доказательство всех приведенных в данном параграфе утверждений можно найти в работе Гёт-це и Тихомирова [24]. торых комплексные гауссовские величины с независимыми вещественной и мнимой частью, выполнен круговой закон. Пастур в работе 1973 г. [26] выдвинул гипотезу, что круговой закон должен быть выполнен для матриц, элементы которых независимы, имеют нулевые средние и конечную дисперсию. Гирко в работе 1984 г. [27] предложил метод исследования асимптотического поведения функции EFn(x,y), опирающийся на подходы, развитые для исследования асимптотики спектра эрмитовых матриц. Им был доказан круговой закон для матриц, элементы которых имеют конечные моменты восьмого порядка и ограниченную плотность распределения. Многие авторы утверждали, что доказательство Гирко некорректно (точнее, оно было неполным). В 1997 г. Бай [28], опираясь на работу Гирко, привел полное доказательство кругового закона, но все при том же весьма ограничительном предположении существования плотности у элементов матрицы. А это значит, исключались даже такие простые матрицы, как матрицы, элементы которых принимают с равными вероятностями значения ± 1. Основной результат, полученный в работе Гётце и Тихомирова, можно сформулировать следующим образом. Пусть 0 < pn 6 1. Введем в рассмотрение бернуллиевские случайные величины sjk, принимающие значения 0 и 1 с вероятностью pn = Pr{ejk = 1}. Определим матрицу X( е ’ = / £ 11X11 £ 21X 21 . . . £n1Xn1 £ 12 X12 £ 22 X 22 . . . £n 1 Xn 2 £ 1 nX 1 n \ £ 2 nX 2 n . . . εnn Xnn Обозначим a1е’,..., An’ собственные числа матрицы X(е’. Пусть fSе’(x,y) = n ^n=1I{Re Aj < x, ImAj < y} и Fn5’(x,y) = E fSe’(x,y) означают соответственно выборочную и ожидаемую спектральную функцию распределения матрицы X(5). Теорема 17. Пусть Xjk, j,k = 1, ...n, независимые случайные величины, такие что E Xjk = 0, E Xjk |2= 1 и существует такая неубывающая функция ф(x), что ^x невозрастающая неотрицательная функция и ф (x) = O (ln8x), и E |Xjk |2ф(Xjk) 6 C < x. Пусть также np- = O (ln2n). Тогда Fn5)(x,y) ^ F(x, y) при n ^ x. (8) Заметим, что при pn = 1 мы получим обычный круговой закон. Наш результат показывает, что этот закон сохраняется и для прореженных матриц с вероятностью прореживания не меньше чем cn1ln2n. Заметим также, что если вероятность прореживания меньше, чем (1 - y)n-1ln n для любого положительного y > 0, то матрица X(5) необратима с положительной вероятностью. Приведенные результаты опубликованы в статье Гётце и Тихомирова [30]. Усиленный круговой закон при аналогичных моментных предположениях был доказан также в работах Тао и Ву [31]. 5. Произведения и степени случайных матриц В настоящем параграфе мы сформулируем некоторые обобщения теоремы Марченко-Пастура на случай произведений и степеней случайных матриц. Также приведем формулировку теоремы о предельном поведении эмпирической функции распределения произведения случайных матриц. Оказывается, спектр произведения независимых случайных матриц с независимыми элементами асимптотически ведет себя так же, как и спектр степени матрицы с независимыми элементами, или как степень величины, равномерно распределенной в единичном круге комплексной плоскости. В этом случае мы можем говорить об «обобщенном» круговом законе. Итак, пусть Xj(V), v = 1,...,m, j,k = 1,..., массив независимых в совокупности комплексных случайных величин с EXj(V) = 0 и EIXjV) |2= 1. Пусть n = p0, и пусть p 1, ■■■ ,pm натуральные числа такие, что pv > p о для всех v = 1 ,...,m. Определим матрицы X(V) размерности pV- 1 х pv для v = 1,..., m и будем называть ее эмпирической спектральной функцией распределения матрицы W, n Fn (x) = ' 52 I {s2 n j=1 Нас будет интересовать асимптотическое поведение математического ожидания эмпирической спектральной функции распределения Fn(x) = E Fn(x). Чтобы описать предельную функцию распределения для функций Fn (x) мы определим преобразование Стилтьеса на множестве функций распределения. Пусть ym = (y 1 ,...,ym), где yi e (0, 1] некоторый параметрический вектор. Ведем в рассмотрение функцию распределения Gy(x), преобразование Стилтьеса которой sy (z) удовлетворяет уравнению m 1 + zsy(z) + (-1)m П(yj - 1 - zsy(z)) = 0. (1) j=1 Уравнение (1) имеет единственное решение с неотрицательной мнимой частью, удовлетворяющее условию - limv^rovV—1 s(vV—1) = 1, и тем самым однозначно определяет преобразование Стилтьеса sy (z) и функцию распределения Gy(x). Заметим, что при m = 1 функция распределения Gy(x) - это просто функция распределения Марченко-Пастура с плотностью g y( x ) = Пу ^(x — a)(b — x)I{x e [a, b]} с a = (1 — Vy)2и b = (1 + Vy)2. Один из основных результатов нашей статьи представляет следующая теорема. Теорема 18. Предположим, что для всех v = 1, . . . , m выполнены условия lim — = yV e (0, 1]. n→∞ pν Далее, пусть для случайных величин Xj(V), v = 1,..., m, j, k = 1,... выполнено условие Линдеберга, т.е. для любого т > 0 дробь Линдеберга X(V) = — Vpv X(V) X11 X(V) X21 . . . X(V) Xpν-1 X(V) X12 X(V) X22 . . . X(V) Xpν-1 X X ( V ) 1 Pv ( V ) 2 Pv \ X( V ) i Xpν-1pν Введем в рассмотрение n × pm матрицу W := П X("). V = 1 Обозначим через s 1 > s2 > ■■■ > sП собственные числа матрицы V = WW* (si, i = 1 ,...,n, - сингулярные числа матрицы W). Здесь и далее A∗ обозначает комплексно сопряженную матрицу A. Функцию равномерного распределения на множестве квадратов сингулярных чисел матрицы W обозначим Fn (x) Ln(т) : = pν-1 pν max — 52 52e X( v ) ।21 {|xj V) i > т vn} ^ 0, 6ν6m np jk jk j=1 k=1 при n → ∞. Тогда функции распределения Fn (x) слабо сходятся к функции распределения Gy (x) с y = (y 1 ,...,ym). Более того, поскольку Gy (x) непрерывная функция распределения, имеет место предельное соотношение Дn = sup |Fn(x) — Gy (x) | ^ 0 при n ^ x. x Замечание 1. При m = 1, как следствие теоремы 18, мы получим теорему Марченко-Пастура о сходимости спектральной функции распределения выборочной ковариационной матрицы. Замечание 2. Особый интерес представляет случай yi = 1 для всех i = 1,...,m. При таком предположении предельным распределением сингулярного спектра произведения матриц будет так называемое распределение Фусса-Каталана, т. е. распреде- ление, моменты которого суть числа Фусса-Каталана C ^К .. Оказывается, предельным распределением сингулярного спектра степени случайной матрицы с независимыми элементами будет также распределение Фусса-Каталана. Именно, рассмотрим квадратную матрицу X = -n (Xj,k) порядка n, где Xjk, j,k = 1 ,...,n независимые случайные величины, и ее m-ю степень W = Xm. Пусть Hn(x) - эмпирическая спектральная функция распределения матрицы WW∗ и Hn(x) = EHn(x) - математическое ожидание эмпирической спектральной функции распределения. Пусть G(x) = Gy0(x), где yо = (1, 1,..., 1). Имеет место следующий результат. Теорема 19. Пусть элементы матрицы X суть независимые случайные величины с нулевым средним и единичной дисперсией. Предположим, что существует такая постоянная C, что supj,k E \Xjk\4 6 C и n Ln(т) := n2E E Xjk 141{IXjk I > ^n} - 0, j,k = 1 при n → ∞. Тогда △ n := sup Hn(x) — G(x) | ^ 0 при n ^ ro. x Распределения Фусса-Каталана возникали ранее в работах по свободной вероятности. В частности, Оравец [32] показал, что степени и произведения так называемых свободных R-диагональных элементов имеют распределение Фусса–Каталана. Таким образом, результаты замечания 2 и теоремы 18 дают соответствующую матричную модель. Случай квадратных гауссовских матриц (y 1 = • • • = ym = 1) был рассмотрен Баника (Banica) и др. [33] (см. Теорему 6.1 в [33]), а также в работе Шпайхера (Speicher) и Минго (Mingo) [34]. В заключение мы обсудим собственный спектр произведения неэрмитовых случайных квадратных матриц. Будем считать, что n = p0= p 1 = • • • = pm• Пусть матрица W = П1= X(V) • Обозначим А 1, ...,An собственные числа матрицы W. Рассмотрим эмпирическую спектральную меру мnm) матрицы W, определенную как равномерное распределение на множестве собственных чисел А 1,..., An. Пусть ^nm) означает математическое ожидание эмпирической спектральной меры матрицы W. Для любого борелевского множества B cR2определим меру vnm)(B) = Eмnm)(B)• Введем в рассмотрение случайную величину ξ на комплексной плоскости, равномерно распределенную в единичном круге. Обозначим G(m)(x,y) функцию совместного распределения вещественной и мнимой части случайной величины ^m, а символом Gnm)(x, у) обозначим функцию распределения, соответствующую мере vnm) на плоскости. Тогда имеет место следующая теорема. Теорема 20. Пусть для независимых в совокупности случайных величин Xj V), v = 1,..., m, j, k = 1,... существуют такие постоянные C > 0 и 8 > 0, что EIXjk12+5 6 C для всех j, k > 1. Тогда △ n := sup IGnm)(x,y) — G(m)(x,y)|^ 0 при n → ∞. x,y Замечание 3. При m = 1, как следствие теоремы 20, мы получим известный круговой закон для случайных матриц. Приведенные в этом параграфе результаты частично опубликованы в работах [35] и [36]. Работа частично поддержана грантами РФ-ФИ№ 09-01-12180-офи_м и РФФИ–ННИО № 09-01-91331-ННИО_а, а также грантом поддержки ведущих научных школ РФ № НШ-4472.2010.1.2. Выборочные ковариационные матрицы
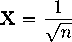
3. Метод Стейна для случайных матриц
Список литературы Предельные теоремы для случайных матриц
- Wigner, E. Characteristic vectors of bordered matrices with infinite dimensions//Ann. Math., 1955. Vol. 62. P. 548-564.
- Wigner E. On the distribution of the roots of certain symmetric matrices//Ann. Math., 1958. Vol. 67. P. 325-327.
- Гирко В.Л. Спектральная теория случайных матриц//Успе
- Arnold L. On the asymptotiv distribution of the eigenvalues of random matrices//J. Math. Anal. Appl., 1960. Vol. 20. P. 262-268.
- Пастур Л.А. О спектре случайных матриц//ТМ
- Марченко ВА. Пастур ЛА. Распределение собственных чисел в некоторых ансам
- Bai Z.D. Convergence rate of expected spectral distributions of large random matrices. Part 1. Wigner matrices//Ann. Probab., 1993. Vol. 21. No. 2. P. 625-648.
- Girko V.L. Extended proof of the statement: Convergence rate of the expected spectral functions of symmetric random matrices tin is equal to O(n-1/2) and the method of critical steepest descent//random Operator and Stoch. Equations, 2002. Vol. 10. P. 252-300.
- Bai Z.D., Miao B., Tsay J. Convergence rates of spectral distributions of large Wigner matrices//Intern. Math. J., 2003. Vol. 1. P. 65-90.
- Gotze F. and Tikhomirov A.N. Rate of con vergence to the semi-circular law//Probab. Theory Relat. Fields, 2003. Vol. 127. P. 228 27
- Bobkov S.G., Gotze F., Tikhomirov, A.N. On concentration of empirical measures and con vergence to the semi-circle law//Journal of Theoretical Probability, 2010. Vol. 23. No. 3. P. 792-823
- Tikhomirov A.N. On the rate of convergence to the expected spectral distribution function of a Wigner matrix to the semi-circular law//SIBAM, 2009. Vol. 19. No 3. P. 211-223.
- Gotze F.; Tikhomirov A.N. The rate of convergence for spectra of GUE and LUE matrix ensembles//Cent. Eur. J. Math., 2005. Vol. 3. No. 4. P. 666-704.
- Тимушев ДА., Тихомиров АН., Холопов А.А. О точности приближения спектра GOE полукру-говым
- Gotze F., Tikhomirov A., Timushev D. Rate of convergence to the semi-circle law for the deformed Gaussian unitary enssemble//Cent.Eur. J. Math., 2007. Vol. 5. No. 2. P. 305-334.
- Wishart J. The generalised product moment distribution in samples from a normal multivariate population//Biometrika, 1928. Vol. 20A. P. 32-52.
- Bai Z.D. Methodologies in spectral analysis of large dimensional random matrices, a review//Statistica Sinica, 1999. Vol. 9. P. 611-677.
- Bai Z.D. Convergence rate of expected spectral distributions of large random matrices. Part II. Sample covariance matrices//Ann. Probab., 1993. Vol. 21. No. 2. P. 649-672.
- Bai Z.D., Miao B., Yao J. Convergence rates of spectral distributions of large sample covariance matrices//SIAM J. Matrix Anal. Appl., 2003. Vol. 25. No. 1. P. 105-127.
- Gotze F., Tikhomirov A.N. Rate of convergence in probability to the Marchenko-Pastur law//Bernoulli, 2004. Vol. 10. No. 3. P. 503-548.
- Gotze F., Tikhomirov A.N. The rate of conver gence of spectra of sample covariance matrices//Теория вероятн. и примен., 2009.
- Tikhomirov A.N. On the rate of convergence to the expected spectral distribution function of sample covariance matrices to the Marchenko-Pastur distribution//SIBAM, 2009. Vol. 19. No. 4. P. 277-286.
- Gotze F., Tikhomirov A.N. Limit theorems for spectra of random matrices with martingale structure//Теория вероятн. и примен., 2007. Т
- Gotze F., Tikhomirov A.N. Limit theorems for spectra of positive random matrices under dependence//Зап. науч. сем. ПОМИ, 2004. Т.
- Mehta M.L. Random Matrices. 2nd ed., San Diego: Academic Press, 1991.
- Pastur LA. Спектры случайных самосопряженных операторов//Ус
- Гирко В.Л. Круговой закон//Теория вероятн. и
- Bai Z.D. Circular law//Ann. Probab., 1997. Vol. 25. P. 494-529.
- Gotze F., Tikhomirov A.N. On the circular law//http://arxiv.org/abs/math/0702386.
- Gotze F., Tikhomirov A.N. The Circular Law for Random Matrices//Ann. Probab., 2010. Vol. 38. No. 4. P. 1444-1491.
- Tao T., Vu V. Random Matrices: The circular Law//Commun. Contemp. Math., 2008. Vol. 10. No. 2. P. 261-307.
- Oravecz F. On the powers of Voiculescus circular element//Studia Math., 2001. No. 1. P.85-95.
- Banica, T. Belinschi, S. Capitaine, M., Collins, B. Free Bessel laws//Preprint arXiv:0710.5931.
- Mingo JA., Speicher R. Sharp Bounds for Sums Associated to Graphs of Matrices//Preprint arXiv:0909.4277.
- Алексеев Н.В., Гётце Ф., Тихомиров АН. О сингулярном спектре степеней и произве
- Alexeev N., Gotze F., Tikhomirov A. Asymptotic distribution of singular values of powers of random matrices//Lithuanian Math. J., 2010. Vol. 50. No 2. P. 121-132.
- Bai Z.D., Silverstein J. Spectral analysis of large dimensional random matrices. Mathematics Monograph Series 2. Beijing: Sciences Press, 2006.
- Ginibre J. Statistical ensembles of complex, quaterninon, and real matrices//J. Math. Phys., 1965. Vol. 6. P. 440-449.


