Predicting Post-craniectomy ICP: A Comprehensive Compartmental Model including Decompressive Craniectomy

Published Online March 2011 in MECS

Many brain pathologies (such as traumatic brain injury, stenosis, or intracranial hemorrage) are direct causes of intracranial pressure (ICP) elevation which induces secondary diseases when out of normal range. A pathological severely high pressure can damage cerebrovascular or even deteriorate the main functional areas such as ectocinerea and cranial nervous system. Thus one of the effective approaches, including decompressive craniectomy (DC), for clinicians to manage brain injury is controlling patient's intracranial dynamics.

Intensive works have been done on the simulation of biological model. Regarded as one of the most sensitive indices characterizing intracephalic condition, the hydraulic pressure of cerebrospinal fluid (CSF), also called as ICP, receives much attention when researchers building models for the intracranial hydrodynamical circulation. In 1973 a single compartment model was proposed by Maumarou [1] who claimed a trivial pressure gradient between ventricles and subarachnoid. Then in his following research [2] the pressure index (PVI) was defined and discussed. Although a comprehensive dynamical model developed by Hoffman [3] after that, more accurate quantitative system had not appeared until Ursino's result in 1988 [4, 5]. As one of the most prolific contributors in simulation area of intracephalic dynamics, he firstly provided a fomulas system describing the interaction of multitude intracranial compartments. On specific regions researches also reached impressive results including computing human intracranial mechanical parameters [6, 7], cerebrovascular autoregulation mechanism [8, 9] and etc. On the other hand of clinical neurology, people have discovered favorable evident for DC on alleviating high ICP from clinical data. A recent review [10] proves that adoption of DC as a resort for middle cerebral artery (MAC) significantly reduces mortality rate of brain injury patients and DC brings greater rate of social rehabilitation than other surgeries [11].

The quantitative models mentioned above base on a generally accepted assumption named as Monro-Kellie (MK) principle: the overall closed intracranial volume of human remains as a constant and the variation of one biological compartment's volume must be equally compensated by some other compartments. Using these lumped-parameter models we are able to analyse the intracephalic dynamics. However few researches have applied them to assist surgical practice such as operation of decompressive craniectomy and estimation of ICP after the surgery. Due to the inaccuracy invasiveness and infectivity of other methods (such as ventricle incision and CSF drainage) of monitoring post-craniectomy ICP, to develop a model which provides reasonable forecast of post-surgery ICP dynamics is necessary and meaningful. Moreover due to the complexity of designating incision area and position, the practice of DC is intricate even for experienced surgeon. As a result we are motivated to give a quantitative criterion concerning the size of skull to be excised in DC and its relationship between postcraniectomy ICP.

To expand the clinical application of mathematical models, the traditional Monro-Kellie principle should be appropriately modified according to the change of specific pathological conditions. Based on the practice of decompressive craniectomy, the DC distensible compartment should be added to the interacted biological compartments system. After that the simulation data can outline the effectiveness of DC, give feasible explanation for specific medical phenomenon, and finally be fitted to describe quantitative relationship between DC bone size and post-craniectomy ICP.

The rest of this article is organized as following structure. In part of model structure we gradually build a compartmental model which combines the biological accuracy and computational feasibility. The lumped-parameter compartmental model proposed by Ursino in 1988 is briefly reviewed and we introduce a novel factor of decompressive craniectomy into the system, which including the deduction of DC distensible volume. In third section of simulation, the parameters are designated according to our available literatures and simulation criteria are presented. An appropriate statistical model is used to fit the resulting data in conclusion part. This paper is finally ended with a discussion about simulating and fitting result from aspects of quantitative model and biological pathology.

• II.    S TRUCTURE OF M ODEL

• A.    Closed Compartmental Model

  By developing lumped-parameter compartmental models, researches have reached many insights on intracranial dynamical system. Among those discoveries the paper published by Ursino in 1988 is one of the most generally cited literatures. It divided the intracranial tissue into four major compartments: arterial blood flow compartment, venous blood flow compartment, brain tissue compartment and CSF circulation compartment. The Monro-Kellie principle is stated by a conservative principle equation as follows:

where Q is the constant volume of skull, V denotes the volume of a compartment. Subscripts a , v , tiss and CSF stand for arteries, veins, brain parenchyma and cerebrospinal fluid respectively. The basic concept of monitoring the ICP dynamics is to depict the ICP waveform against time axis under different pathologies. Therefore a nature method for researchers to reach there goal is differentiating (1) with respect to time:

dV a dV v d Vcsf dV tiss

---+---+-----+----= 0

dt dt dt dt

The next step is to analyze individual compartments in (2), which every derivative component can be solved of presented with human brain's biological properties. Referring to present literatures [12, 13, 14], following equations provide a straightforward depiction of dynamics of intracranial pressure in different compartments.

dV a               dP a dP ic

----= mbe (Pa Pc)(---) dt                   dt     dt dVv

= 0 dt

dV cSF              P c - P ic   P ic - P vs

—■— = qf - q0 =---(5)

dt                 R f         R 0

where P a , P ic stand for arterial pressure and intracranial pressure respectively, and m , n are constants; P c , P vs are capillary pressure, venous sinus pressure, R f , R 0 denote CSF formation and absorption resistances. Detailed deduction and substitution of parts in (3) (4) (5) necessary for further simulation are presented in appendix from App. (1)—(5).

• B.    Generalized MK Principle

As mentioned above the MK principle is extensively cited to present the balance of intracranial volume for closed skull. However after decompressive craniectomy brain tissue and dura meter close to the bone window will be usually distensible by high ICP to gain extra compensation volume. And this situation is much more common for patients who encounter secondary intracranial hypertension.

From this aspect it is reasonable to consider DC factor when we are studying on patient's post-craniectomy ICP dynamics. We thus take the assumption that the distended volume caused by secondary hypertension is one of the major components of the compartmental system discussed in previous section (showed by Fig.1). Thus the overall volume relationship presented by (1) should be modified as follows:

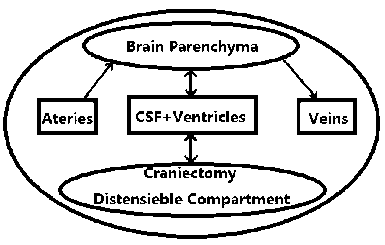
Figure 1. Compartmental model including craniectomy compartment.

where Vdist stands for the distended volume on DC area, namely the volume of distensible craniectomy compartment. Differentiating in two sides of (6) leads to dVa dVv dVcsf   dVtiss dVdist

---+    +------+-----=----- (7) dt     dt dt       dt dt

In (6) when the distensible craniectomy volume is designated as 0, the equation would be degenerated to the model of (1) under traditional MK principle. However our major work is to find a method to decompose (6) by relating compartment V dist with ICP. In this way the distensible component ICP can be added to the system. In following section an analytical method of mechanics is introduced to solve the task above.

• C.    Distensible Volume Computation

In the practice of decompressive craniectomy, the surgeon usually chooses a clinically advantageous shape size for ICP reduction. At the beginning of our research we start with a rectangular area. But it is replaced by an ellipse (Fig. 2) area which is much more convenient for clinical operation.

Additionally the dura mater is usually distended to a camber shown by Fig. 3. The higher the intracranial pressure is, the larger the camber will become. Hereto the introduction of craniectomy compartment and qualitative analysis of DC factor is finished. The last step for model construction is to find a method to compute distensible volume.

Might as well we accept several basic mechanical assumptions in order to apply the deflection solution:

• 1)    Brain dura meter is an isotropic elastic membrane;

• 2)    The bone flap excised from skull is a regular ellipse;

• 3)    Post-craniectomy dura mater on the bone window is an edge-clamped membrane under uniformly distributed

Let W(x, y) be the deflection function: the vertical displacement of point (x, y) on a membrane under uniformly distributed pressure. Here a usual form of deflection solution is cited from [15]:

w ( x , y )

Pc ( xr + yr — 1) 2 ab

_ , 3     2      V

• ⁸ D (-Г +    + ,4

a  ab b where P c is the intracranial pressure vertical to dura mater, a andb denote the major/minor semi axis of craniectomy and D is bending rigidity.

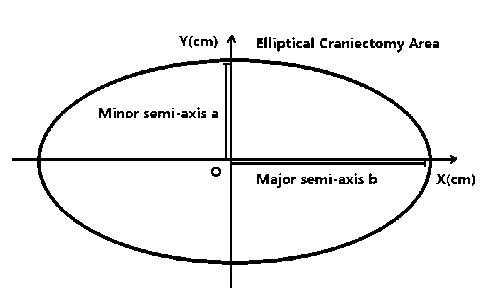
Figure 2. Elliptical area of decompressive craniectomy.

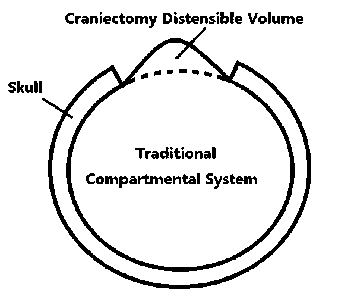
Figure 3. Compartment distended by high post-craniectomy ICP

Thus the integral of deflection function on the elliptical craniectomy area leads to the distensible craniectomy volume:

V ist_t = JJ w ( x , У ) dxdy =----- PP c ^ab^ ----3- ⁽¹⁰⁾

»          24 D (4 ++ a4   a2b2 b4

and                 dVdiS^ = c ■ f (a, b) ■ dPiC(11)

dtdt where one can get the meanings of related symbols by comparing (10) and (11).

Hereto a dynamical relationship between craniectomy compartment and ICP has been built and the major five parts—arterial and venous blood compartments, brain parenchyma compartment, CSF circulation compartment, and distensible craniectomy compartment have all been decomposed to be presented by ICP. The following task is to simulate the intracranial pressure dynamics and to quantitatively describe the effectiveness of DC.

Ш . Numerical Simulation

In sections above the systematic equations have been built for intracranial hydrodynamics. To solve the differential equations related to ICP we should use appropriate parameters and numerical algorithm that we have known. Additionally simulation criterion should be established to achieve more accurate data for further manipulation.

• A.    Parameters Designation

Due to complexity of collecting parameters under practical pathologies, those values are simply adopted from recent researches [5, 8, 9, 10, 22] of a normal people in Table I.

TABLE I.

I NTRACRANIAL P ARAMETERS

symbol	biological parameter	value	unit
m	constant	-10.31
b	constant	-0.012
K R	constant	4910
D	constant	0.4744
C an	constant	0.15	mmHg ⋅ ml - 1
K E	elastance coefficient	0.26	ml - 1
R f	CSF formation resistance	2380	mmHg ⋅ S ⋅ ml - 1
R 0	CSF absorption resistance	49.37	mmHg ⋅ S ⋅ ml - 1
R pv	proximal venous resistance	1.24	mmHg ⋅ S ⋅ ml - 1
P vs	venous sinus presure	6.00	mmHg

• B.    Simulation Criterion

From the above differential equations, ICP is a function, written as P ic ( t ) = P ic ( a , b , P a ( t ), t ) , of DC bone flap size and the waveform of input arterial pressure P a . Therefore detailed simulation point of DC size including minor and major semi-axis of the ellipse should be designed.

In history Ursino’s work in 1988 has been cited most frequently when building the mathematical model and discussing some basic pathologies. Referring to the first part of his work in 1988 [4], two sine waves were subtracted from each other to present the systematic arterial pressure waveform:

π

P a = 17.5sin(2 πt - ₂ ) - 12.5sin(4 πt ) + 100 (12)

Fig. 4 shows the waveform of input arterial pressure in two cycles of and one second is the frequency of heart pulsation.

Additionally the second part of his work in 1988 [5] provided a suggestion for simulating the pathological high intracranial pressure: setting the initial value of ICP higher beyond normal range in its dynamical equation. Here the initial point of ICP value is set as 13mmHg which is slightly lower than normal maximum pressure. Finally the simulation point pairs of minor semi-axis a and major semi-axis b is specified as follows: (0,0), (0.7,0.8), (1.2,1.3), (1,2), (2,2.4), (2.5,3.5), (3,4), (3.5,5), (4,5.5), (5,6), (5,7), (6,8), (7,8), (7,9), (8,10), (9,10), (9,12), (10,12), (11,12), (13,14), (15,16), (17,18), (19,20). The unit is centimeter and centimeter square for length and area respectively. In this paper we solve the differential equations with ODE45 in matlab with 4th order Runge-Kutta algorithm.

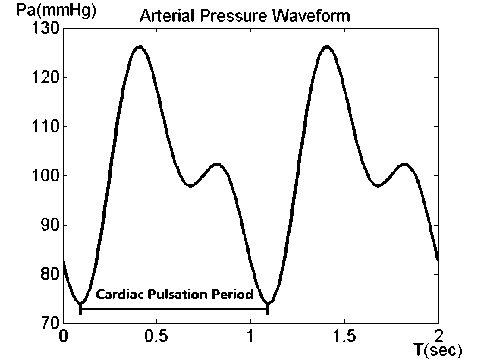
Figure 4. Input Arterial Pressure Waveform.

• IV. Discussion

• A. Simulation Data

Based on the above assumptions and deductions, final differential equation App. (6) on ICP is achieved in Appendix C. This equation provides a mathematical dynamical model of intracranial pressure under the pathology of secondary intracranial hypertension after decompressive craniectomy. By discretizing this equation and plotting its numerical solution, the dynamics of postcraniectomy ICP will be intuitively understood.

From Fig. 5, the first qualitative result we can extract is the monotonically decreasing relationship between average intracranial pressure and the craniectomy size. Starting with a morbid value slightly higher than 15mmHg, the average ICP receives an obvious reduction when the craniectomy size exceeds 100 square centimeters. Then the decreasing tendency, denoted by second derivative of the curve pointed by triangles in Fig. 5, slows down when the DC size is larger than 200 square centimeters.

When the bone size of decompressive craniectomy reaches 224 square centimeters, the average ICP decreases to the upper level of normal ICP range. This situation indicates that under the pathology with ICP of 13mmHg as its initial value, adopting the craniectomy size larger than 224 square centimeters would results in a significant alleviation of intracranial hypertension and reduces ICP to normal range. However after 400 square centimeters larger DC size cannot reduce ICP effectively as to the extremely plain tail of the curve. Therefore when encountered with pathology discussed above, the optimal interval of craniectomy size should be given as from 100 to 300 square centimeters. And the craniectomy sizes out of this optimal interval would not be suggested by our model. With regard to other specific diseases similar method can be used by setting a correspondent initial ICP value to mimic a pathological state. However this paper leaves some special diseases which have difference pathological mechanisms for further studies.

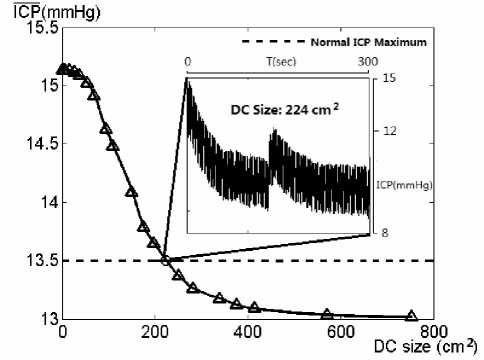
Figure 5. Simulated average ICP values.

Therefore Gaussian fitting model is more appropriate for this situation and is applied as the fitting curve of average ICP values against craniectomy size.

Pressure(mmHg)

20--------

15-

$ ICP Range О ICP Maximum + ICP Minimum

TABLE II.

G AUSSIAN M ODEL P ARAMETERS U NDER 95% C ONFIDENCE B OUND

	Value	Confidence Interval
a 1	1.99	(1.787, 2.193)
a 2	39.37	(-3.663e5, 3.671e5)
b 1	8.062	(-5.95, 22.07)
b 2	-1.814e5	(-1.538e8, 1.534e8)
c 1	163.3	(146.3, 180.3)
c 2	1.733e5	(-7.29e7, 7.324e7)
SSE	0.0113
R-square	0.9991

10-

5-

13.5

14.5

**

15 ___   15.5

ICP(mmHg)

Figure 6. Relationships between characteristic values of ICP wave

In Fig. 6, different characteristic values of an ICP waveform is compared with its average ICP value. First the minimum value is almost independent on the craniectomy size. More importantly the maximum value and range of an ICP waveform is linearly dependent on its average ICP. Therefore when depicting the dynamics of an ICP wave, we can use the average ICP value to present its general action.

B. Statistical Model of ICP-Size Curve

The above section presents some significant results with natural language. On behalf of more accurate depiction and prediction of characteristics of postcraniectomy ICP waveform, we should build a statistical model whose parameters can be fitted by simulation result in previous sections.

At first sight the S-shaped curve of average ICP incurs the possible use of logistic fitting model. However as show by Fig. 5, the vertical axis value—simulated average ICP value dies rapidly and become obviously plain when the horizontal axis value is relatively large, which contradicts the exponential growth of logistic tails.

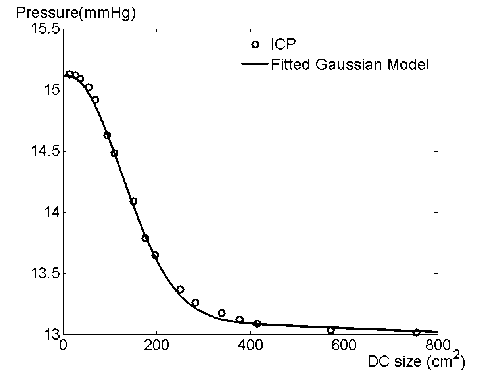
Figure 7. Fitting result of Gaussian model

For the convenience and accuracy of fitting, the model is set as 2nd order Gaussian:

_____            _ ( ⁵ - b ¹ ) 2          _ ( ⁵ - b ² ) 2

ICP ( 5 ) = a 1 ■ e c ¹     + a 2 ■ e    ^{c 2}         (13)

where S stands for the craniectomy size, and the a 1, 2 , b 1 2 , c 1, 2 are parameters of Gaussian fitting model. Fig. 7 presents the comparison between simulated average ICP values and fitted Gaussian curve. The Table II gives statistical results on Gaussian model parameters.

V . Conclusion

Traditional investigations on simulation model of human intracranial dynamics usually incorporate

compartments of vascular system, CSF circulation, and brain parenchyma. In this study we generalize the application of traditional model to clinical operation of decompressive craniectomy. With the computation of elliptical deflection solution on DC area, the craniectomy compartment is appropriately connected to ICP and added to the traditional dynamical system. Additionally through our simulated data a statistical model is proposed for more accurate forecast of post-craniectomy ICP. The Gaussian model gives a good fitting of relationship between average intracranial pressure and DC size. Thus before the practice of DC, surgeons can refer to our results as a possible suggestion for controlling postcraniectomy ICP.

Some aspects of acute intracranial hypertension have been explained by our model. However special pathologies (such as chronic hydrocephalus, morbid ICP caused by encephalic dngioma and etc) cannot be included here. To account for these factors other mechanisms (such as vascular autoregulation under tissue compression, CSF formation and absorption and etc) should be detailedly studied. Furthermore the biological meanings of Gaussian parameters need more researches or even possibly more reasonable model would be proposed in future. Much work remains to be done in generalizing our model, but adding the craniectomy compartment to previous system appears to be a good start of more clinical applications of mathematical models.

A PPENDIX R ELATED D EDUCTION

• a)    Conservative principle of flux at the capillary

Venous pressure approximately equates to intracranial pressure, the implies that

P a — P c   P c — P ic P c — P ic

------=------+ —---- (App. 1) Ra       Rf       Rpv which implies dPic                 Ke • Pic

A CKNOWLEDGMENT

This work was supported by Innovation Fund of Huazhong University of Science and Technology (Grants 2010MS131) and Science and Technology Innovation Fund for College Student of Huazhong University of Science and Technology (Project No. 136). Our project was also supported by National Science Foundation of China (Grants No. 60773195).