Prediction of formation of competing phases during the growth of Cr2GaC THIN FILMS ON MgO(111)

Currently, one of the most promising areas of research related to the synthesis of new materials is the study of formation processes and physical properties of MAX phases, the family of which is shown in Fig. 1. MAX-phases posess low density, high values of thermal and electrical conductivity, strength, low elastic modulus, excellent corrosion resistance in aggressive liquid media [5–7], resistance to high-temperature oxidation and thermal shock [8–10], and are also easily machined [11; 12], have a high melting point [13] and are quite stable at temperatures up to 1000 ° C and above [14].

It is well known that thin films of MAX phases are mainly synthesized applying physical methods, such as magnetron sputtering of pulsed layer deposition. A comprehensive study of magnetic properties requires high quality magnetic thin films of MAX-phases. Films of the highest quality are defined as single phase, monocrystalline and smooth.

Рис. 1. Периодическая таблица элементов, образующих наноламинаты общего состава [2]

• Fig. 1.    The periodic table of the elements constituting the nanolaminates of general composition [2]

The quality of the resulting films is influenced by such factors as precipitation temperature, pressure, power supplied to magnetrons, i.e., the outgoing / incoming material flow, as well as the choice of substrate. For the synthesis of MAX phases, it is necessary to consider competing binary or ternary phases that are close in composition and / or structure.

The growth of the Cr 2 GaC epitaxial film is accompanied by the growth of the Cr 3 Ga phase, which is not predicted to be competitive in terms of stoichiometric chemical composition [15]. Substrate, in turn, can radically change the situation, as is observed in the case of Mn 2 GaC. Under the same growth conditions, there was no visible signal of the MAX phase on any substrate other than MgO [15].

Thus, our task is to consider the effect of a change in the stoichiometry of the atomic flux on the thermodynamic advantage of phase formation, and also to take into account the role of the interfaces between the substrate and the MAX phase and competing phases.

Results and discussions

In this work, we study the MAX phase of Cr 2 GaC. To study this compound, it is necessary to consider the Cr-Ga-C system. The challenge is to consider all possible reactions between pure elements available in varying quantities. Below is an example of the reaction.

2xCr + xGa + xC → Cr GaC + [competing] + α Cr + β Ga + θ C. (1)

In this example, pure elements are available in quantities corresponding to the stoichiometry of the MAX phase, i.e. Cr: Ga: C = 2: 1: 1 on the right-hand side of the equation; the coefficients at the remainder of pure elements are symbolised by Greek letters. The competing phase can be any of seven possible phases in the Cr-Ga-C system: CrGa 4 , Cr5Ga 6 , CrGa, Cr 3 Ga, Cr 3 C2, Cr 7 C 3 , or Cr 23 C 6 .

The enthalpy of one specific reaction was calculated not only in the case of elements presence in quantities corresponding to the stoichiometry of the MAX-phase, i.e, Cr: Ga: C = 2: 1: 1, but also for all possible ratios.

Due to the large amount of calculations required, it was decided to write a special code in the "Matlab" software package. The outer cycles are the cycles for i, j, k, which mean the atomic fractions of chromium, gallium and carbon, respectively. When establishing the boundaries of the cycle, it was taken into account that their sum is 1. These are the cycles that are responsible for calculating the enthalpy of each specific reaction, not only in the case of the elements in quantities corresponding to the stoichiometry of the MAXphase, i.e. Cr: Ga: C = 2: 1: 1, but also for all possible ratios. Each phase was assigned to a corresponding set of three numbers, the first of which means the number of chromium atoms in the formula unit of the compound, the second - the number of gallium atoms, the third – carbon. For example, the set 703 was assigned to the Cr7C3 phase, and to the Cr3Ga – 310 phase was assigned. Thus, the netlist was transformed into a list of sets of numbers, accessing to which in the program code was reduced to accessing certain elements of the matrix. Each set of three digits also had a sequential number, which corresponds to the enthalpy of the encoded phase. The need to separately access each type of incoming into the phase atom was due to the need to calculate the atomic balance in the equation and to search for the largest coefficients for all phases in the right-hand side of the equation. The implementation of the latter in the program code was based on the idea of checking whether it is possible to form any phase in the right-hand side from the remainder of free atoms. By introducing such additional internal cycles, it was found that in some cases the phase coefficients on the right-hand side of the equation are really different from the units, i.e., from how it was written at the beginning when describing the general form of reaction equation (1).

In this paper, three different types of reactions have been considered. The types are determined by the number of different competing phases. The first type contains С ¹ = 7 various reactions with a competing phase; the second type contains С ² = 21a different reaction, with each containing a unique pair of competing phases; the third type contains С ³ = 35 different reactions, with each containing a unique triple of competing phases. In addition, each reaction can be recorded without the MAX phase on the right side of the equation.

Since the variable parameter in the calculation model was the ratio of the three different pure elements numbers, it was agreed to present the results in the form of ternary diagrams, namely, in the form of a set of three ternary diagrams for each case (for each of the arrows in Scheme 1). Below, only results for the first and second types of reactions in the presence of the MAX-phase on the right side of the equation are given (Fig. 2, 3).

Each point on ternary diagrams in Fig. 2 corresponds to one defined ratio Cr: Ga: C. For this ratio, 7 enthalpies were calculated and compared. Then the most negative value was determined and the point was shown in the color corresponding to the competing phase, the formation of which leads to the greatest energy release. Areas and their boundaries are easily visible on the charts. This allows us to judge, for example, the experimental error in the ratio of the elements number: by comparing the expected and obtained competing phases, it is possible to determine which element was taken in excess. The third diagram (Fig. 2, в ) shows the difference between the heats of formation of the two most thermodynamically favorable competing phases. It is noteworthy that the leading phases are the same, they only change their areas.

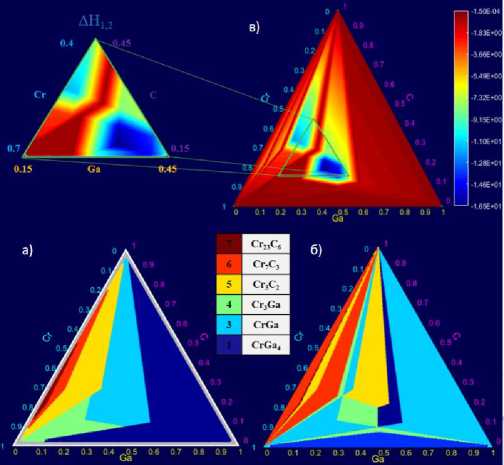
Рис. 2. Диаграммы номеров наиболее выгодных конкурирующих фаз

(в случае образования MAX-фазы и одной конкурирующей фазы): а – первый кандидат; б – второй кандидат; в – разница между эффективными теплотами образования (кДж/моль*атом) двух наиболее термодинамически выгодных конкурирующих фаз

• Fig. 2.    Diagrams of the numbers of the most favorable competing phases

(in the case of the formation of the MAX-phase and one competing phase):

(bottom left) the first candidate; (bottom right) the second candidate; (top right) the difference between the effective heat of formation (kJ/mol*atom) of the two most thermodynamically favourable competing phases

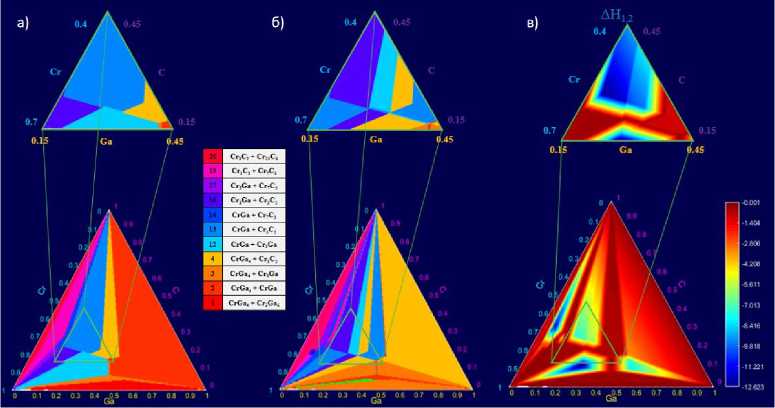
Рис. 3. Диаграммы номеров наиболее выгодных конкурирующих фаз (в случае образования MAX-фазы и двух конкурирующих фаз): а – первый кандидат; б – второй кандидат; в – разница между эффективными теплотами образования (кДж/моль*атом) двух наиболее термодинамически выгодных конкурирующих фаз

• Fig. 3.    Diagrams of the numbers of the most favorable competing phases

(in the case of the formation of the MAX-phase and two competing phases): (bottom left) the first candidate; (bottom right) the second candidate; (top right) the difference between the effective heat of formation (kJ/mol*atom) of the two most thermodynamically favourable competing phases

The same was done in the case of two competing phases (Fig. 3), i.e, for the second type of reactions. It can be seen that the group of leading phases remains the same again: CrGa, Cr 3 Ga, Cr 3 C 2 , in this case we are simply dealing with their combinations.

According to the effective heat of formation model [2], one of the most significant factors influencing the formation of phases is: the larger the number of atoms in the unit cell, the more difficult the formation of the phase is (Table 1).

Table 1

Number of atoms in unit cells of different phases

Cr 3 Ga 21 atoms in unit cell	CrGa 92 atoms in unit cell	Cr 3 C 2 20 atoms in unit cell	Cr 2 GaC 18 atoms in unit cell
о*»? *%#	Т^^&5^? р v^^o •	гЯ^1	Nk^lS^H* О
			°      °
о^^Ь®	/Wv^o’ ° о	о 00 1»е	0 <^=5^=4

Table 2

Orientation relations and the density of near-coincident sites at the interface between the MAX-phase Cr 2 GaC and MgO [3;4]

Interface	u11v11w11	U12v1 2w12	u21v21w21	u22v22w22	h1k1l1	h2k2l2	Density of nearcoincident sites, R
MgO||Cr2GaC	[011]	[020]	[10-1]	[200]	(–11-1)	(001)	0.0418
MgO|| CrGa	[0-11]	[11-2]	[–1.578 – 2.989 1.071]	[4.61 1.49 4 0.0]	(–11-1)	(–5.09 2.989 0.507)	0.0545
MgO|| Cr3Ga	[0-11]	[11-2]	[010]	[001]	(–11-1)	(001)	0.0887

In addition, consideration of the possible interface between CrGa and the surface of magnesium oxide MgO (111) applying the coincident lattice method reveals the preferability of the Cr 3 Ga phase over CrGa (Table 2).

Conclusion

During the formation of magnetic thin films of MAX phases, there are only three most thermodynamically favorable phases: CrGa, Cr 3 Ga, and Cr 3 C 2 .

Although the enthalpy of CrGa formation is most negative, according to the coincident lattice method the formation of the Cr 3 Ga phase with fewer atoms is more likely in a unit cell, which has been experimentally confirmed [15].