Предкоррекция фазочастотной характеристики цифровых фильтров

В задачах цифровой обработки сигналов [1; 2] реализация фильтра с нулевой фазочастотной характеристикой (ФЧХ) относится к нереализуемым задачам, так как она подразумевает нулевую задержку сигнала. Однако ее реализация невозможна только в реальном времени. Вне реального времени существуют решения для цифровой фильтрации с нулевой ФЧХ. Для фильтров с бесконечной импульсной характеристикой (БИХ) существует оригинальное решение относительно реализации цифрового фильтра за счет двукратной фильтрации сигнала в прямом и обратном направлениях последовательности отсчетов с помощью стандартного алгоритма фильтрации, что позволяет получить фильтр с нулевой фазочастотной характеристикой. Один из наиболее известных примеров – функция filtfilt [3] в среде MATLAB. Для фильтров с конечной импульсной характеристикой (КИХ) существуют решения на основе задержки сигнала [4–6].

Однако также известна реализация цифрового фильтра с нулевой ФЧХ в реальном времени, в которой сохраняется фундаментальный принцип задержки. В качестве примера такой реализации рассмотрим гармонический сигнал. Если допустить, что выходной сигнал отстает на один или несколько периодов, то фактически фазовый сдвиг будет равен нулю. Распространяя на полосу частот можно получить утверждение, что если в пределах полосы фазовый сдвиг между входным и выходным сигналом равен нулю, при том, что имеет место фактическое отставание сигнала, то такая система окажется реализуемой. Реализация такой системы возможна с помощью структурной схемы, приведенной на рисунке 1 [7].

Структурная схема содержит идентичные полосные фильтры 1 и 4, блок 2 выделения несущего сигнала с удвоенной частотой, умножитель 3.

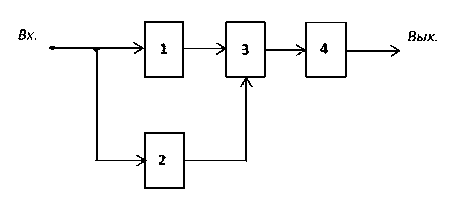
Рисунок 1. Структурная схема фильтра с нулевой фазочастотной характеристикой

В работах [8–10] для реализация данной структуры использовались КИХ фильтры, реализуемые методом частотной выборки. Целью данной работы является реализация модели данной структурной схемы на основе цифровых БИХ фильтров, так как данные фильтры обладают, как правило, повышенным быстродействием за счет рекурсивных схем реализации. Их использование предпочтительно, однако нелинейность ФЧХ фильтров ограничивает их использование.

Постановка задачи

Фазочастотная характеристика цифровых фильтров определяется алгоритмом их работы. Например, если используются только отсчеты входного сигнала, то создаются условия реализации линейной ФЧХ. Если используются отсчеты входного и выходного сигналов, то реализовать линейную ФЧХ становится невозможно. Рекурсивные БИХ фильтры требуют выполнения условий устойчивой реализации. Достоинством последних фильтров является более компактный алгоритм работы. Общим недостатком цифровых фильтров является большой диапазон изменения фазового сдвига в рабочей полосе, зависящий от порядка фильтров. Это приводит, например, к многозначности частот с одинаковым фазовым сдвигом [7].

Актуальной задачей является приведение ФЧХ цифровых фильтров к заданному виду в реальном времени. Оптимальным видом ФЧХ после коррекции будем считать нулевой эквивалентный фазовый сдвиг в полосе пропускания фильтра, нулевую ФЧХ, которая, к тому же, линеаризуется [10].

Описание работы структурной схемы

Рассмотрим реализацию структурной схемы, приведенной на рисунке 1. В устройстве использовано известное свойство преобразования узкополосных сигналов путем гетеродинного переноса их спектров в заданные области частот. Если частота гетеродина больше средней частоты узкополосного сигнала, и после перемножения выделяется спектр с разностными частотами, то начальные фазы гармоник вычитаются из начальной фазы сигнала гетеродина.

Продемонстрируем работу устройства на примере прохождения через него гармонического сигнала, частота которого находится в полосе пропускания фильтров 1 и 4. Изменениями амплитуды пренебрегаем.

Входной сигнал устройства:

ивх = sin(® t + 0)

на выходе фильтра 1 получит дополнительный фазовый сдвиг:

u1 = sin(at + 0 + p).

Входной сигнал устройства на выходе блока 2 после удвоения частоты примет вид:

u 2 = sin(2»t + 20 +1//)

В умножителе 3 оба сигнала перемножаются. С помощью фильтра 4 выделяется сигнал с разностью частот перемножаемых сигналов, который примет вид:

ивых = sin(2at - at + 20 - 0 - ф + ф + i//) =

= sin(at + 0 + ^) .

Видно, что фазовые сдвиги в фильтрах 1 и 4 компенсируют друг друга. В выходном сигнале возникает фазовый сдвиг Ψ , вызванный прохождением сигнала через блок 2, и его необходимо уменьшить при реализации устройства до возможного минимума.

Компьютерное моделирование

Анализ работы указанного устройства при прохождении через него узкополосного сигнала и при использовании рекурсивных фильтров высокого порядка потребовал дополнительных исследований, которые выполнены с помощью модели устройства в среде MATLAB.

На рисунке 2 приведена разработанная компьютерная модель устройства предкоррекции ФЧХ рекурсивного цифрового фильтра и вспомогательные блоки.

Модель содержит три идентичных полосных фильтра Filter 2, 3 и 4. Коррекции подвергается ФЧХ фильтра 2. Фильтр 3 необходим для внесе-

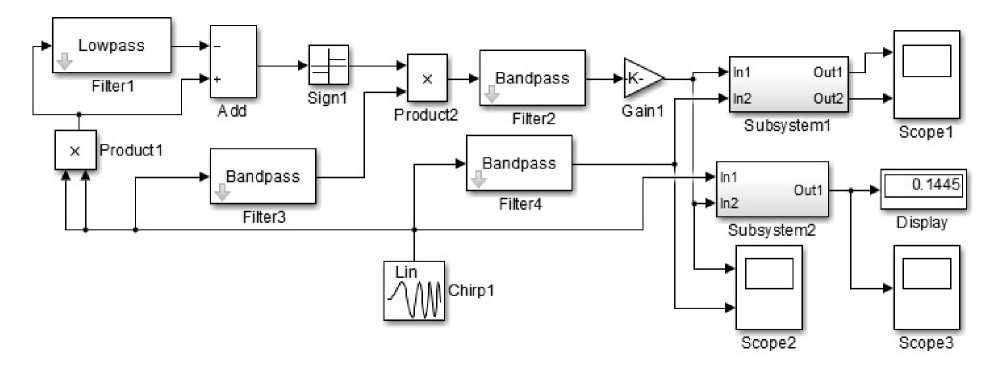
Рисунок 2. Компьютерная модель цифрового фильтра с нулевой ФЧХ

ния в сигнал необходимого фазового сдвига, а контрольный фильтр 4 используется для сравнения результатов эксперимента. Перемножитель Product 1, фильтр нижних частот Filter 1, блок вычитания Add и ограничитель амплитуды Sign необходимы для выделения из входного узкополосного сигнала несущего колебания с удвоенной частотой. Во втором перемножителе Product 2 перемножаются несущее колебание с удвоенной частотой и выходной сигнал фильтра 3, получивший дополнительный фазовый сдвиг относительно входного сигнала устройства.

Умножение входного сигнала устройства на себя дополнительно дает постоянную составляющую:

sin2 a = 0.5(1 - cos 2a).

Постоянная составляющая выделяется фильтром 1 и вычитается из сигнала. Ограничитель Sign 1 необходим для снятия амплитудной модуляции несущего колебания.

Результат второго перемножения определяется выражением:

sin в ( — cos 2 a ) =

= 0.5 (sin (в - 2a - n) + sin (в + 2a + n)).

Второе слагаемое не попадает в полосу пропускания фильтра 2 и исключается. На выходе фильтра 2 будет сигнал вида sin ( 2 a - в ) , сиг— нал с частотой входного сигнала.

Для снятия частотных характеристик модель содержит генератор гармонического сигнала с линейно изменяющейся частотой Chirp1, блок синхронных детекторов Subsystem 1 и блок измерения текущего фазового сдвига Subsystem 2. В целях визуального контроля результатов используются осциллографы Scope 1, 2, 3 и Display.

Разработанная модель позволяет исследовать предкоррекцию любых цифровых полосных фильтров, а также сформировать алгоритм про-

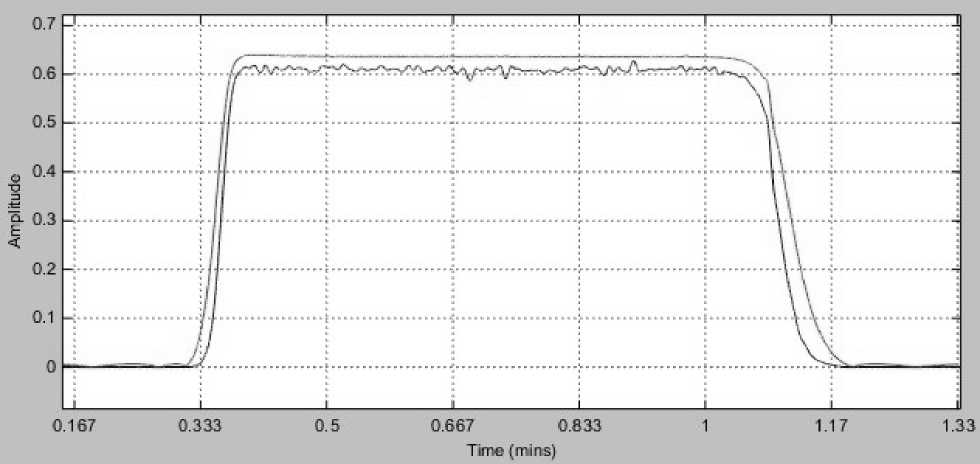
Рисунок 3. АЧХ рекурсивного фильтра используемого в модели

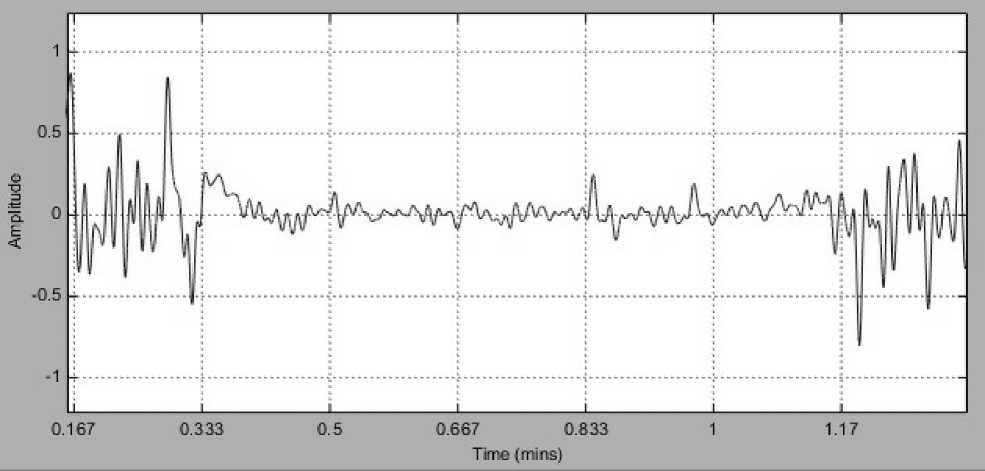
Рисунок 4. Результат работы модели – выходной сигнал фазометра

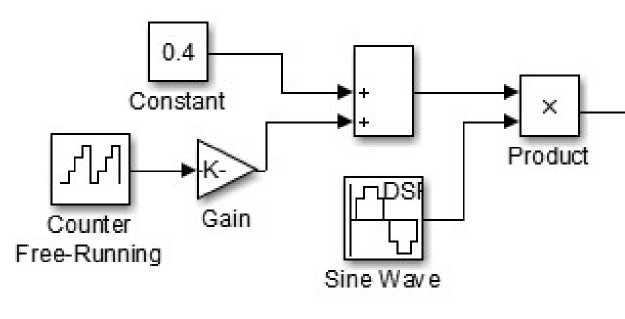
Рисунок 5. Модель генератора периодического узкополосного сигнала

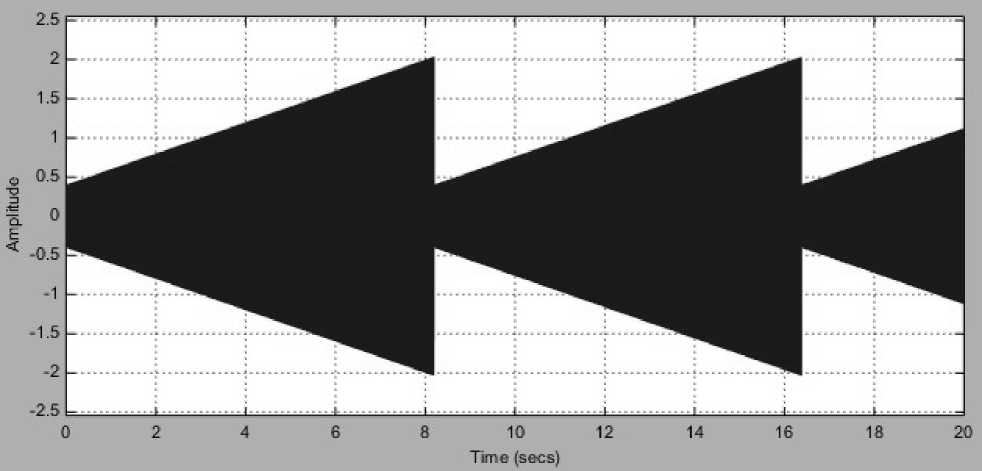
Рисунок 6. Выходной сигнал генератора периодического узкополосного сигнала граммной реализации цифровых фильтров с нулевой ФЧХ, работающих в реальном времени.

В качестве доказательства эффективности предварительной коррекции приведем результаты эксперимента, выполненного с помощью данной модели.

В эксперименте использовался рекурсивный фильтр, АЧХ которого приведена на рисунке 3 (верхняя кривая). ФЧХ фильтра является нелинейной, а фазовый сдвиг в полосе пропускания изменяется на 15 радиан.

Эквивалентная АЧХ устройства с предварительной коррекцией приведена на рисунке 3 (нижняя кривая). Полоса пропускания стала уже, так как сигнал проходит через каскадное соединение двух одинаковых фильтров 3 и 2.

Эквивалентная ФЧХ устройства с предварительной коррекцией приведена на рисунке 4. Пренебрегая погрешностью измерения фазового сдвига из-за быстрого сканирования будем считать ФЧХ нулевой. Измерение фазового сдвига выполнялось на каждом периоде сигнала. Исследовалось прохождение через фильтр произвольного периодического узкополосного сигнала с предварительной коррекцией, который формировался с помощью модели, представленной на рисунке 5, и вид которого приведен на рисунке 6.

На рисунке 7 приведены огибающие выходных сигналов контрольного фильтра 4 (верхняя кривая) и фильтра с предварительной коррекцией (нижняя кривая).

Видно, что введение предварительной коррекции существенно не сужает полосу пропускания фильтра, незначительно увеличивает задержку сигнала, а характер переходного процесса на фронтах сигнала остается прежним.

Согласно результатам выполненных исследований можно сделать следующие выводы:

Использование разработанной технологии предварительной коррекции ФЧХ рекурсивных полосных цифровых фильтров позволяет получить нулевую линейную эквивалентную ФЧХ в реальном времени.

Разработанная технология предварительной коррекции реализуется с помощью программных средств.

Введение предварительной коррекции незначительно влияет на полосу пропускания фильтра, на задержку сигнала и на характер переходных процессов, в сравнении с фильтром без предварительной коррекции.