Предсказание и уточнение ионосферных поправок в радионавигации на основе машинного обучения и фильтра Калмана с использованием данных из моделей электронной концентрации и радионавигационных измерений

Современные системы спутниковой навигации, такие как GPS и ГЛОНАСС, широко используются в различных сферах деятельности – от транспорта и геодезии до навигации – в условиях сложной среды. Одним из ключевых факторов, влияющих на точность и надежность навигационных решений, является ионосфера, которая вызывает задержки радиосигналов и приводит к ошибкам в определении положения. Точные оценки ионосферных поправок являются необходимым условием повышения точности навигационных систем, особенно в условиях динамично меняющейся ионосферной среды [1].

На сегодняшний день существует множество методов моделирования и измерения электронной концентрации в ионосфере [2–4], однако их интеграция и использование для повышения точности коррекций остаются актуальными задачами. В последние годы особое внимание уделяется применению методов машинного обучения [5; 6] для предсказания ионосферных параметров, что позволяет получать более точные и своевременные оценки.

Целью данной работы является разработка и внедрение метода, объединяющего предсказания вертикальной электронной концентрации VTEC (Vertical Total Electron Concentration). VTEC показывает количество электронов в вертикальной колонне ионосферы над определенной точкой. Измеряется в единицах TECU (Total Electron Content Units), где 1 TECU = 1016 электронов на квадратный метр. Высокие уровни VTEC могут вызывать значительные задержки и искажения радиосигналов, особенно в системах GPS и других спутниковых навигационных систем. Это происходит из-за преломления и рассеяния электромагнитных волн в ионосфере. Также они влияют на фазу и группу скорости радиоволн, что может приводить к ошибкам в позиционировании и навигации.

Метод машинного обучения очень востребован, поскольку совмещает в себе два подхода – прогнозирование на уровне машинного обучения и вычисление в реальном времени на основе текущих радионавигационных измерений [7]. Метод на основе машинного обучения имеет такие преимущества, как большой объем накопленных данных, вычисление правильных закономерностей и построение точных моделей предсказания [8]. Метод на основе текущих радионавигационных измерений позволяет гибко реагировать на изменения окружающий среды, которые приводят к отхождению от ранее рассчитанной модели, поскольку реальное радионавигационное измерение и накопление данных в реальном времени позволяют оперативно корректировать модели и повышать их точность.

Предсказание и уточнение ионосферных поправок в радионавигации на основе машинного обучения и фильтра Калмана с использованием данных...

Использование фильтра Калмана в качестве инструмента интеграции этих источников данных позволяет повысить точность и надежность оценки ионосферных задержек [9], что особенно важно для повышения эффективности и безопасности навигационных систем в условиях изменяющейся ионосферной среды, поэтому в данном исследовании совмещены оба подхода.

Применение машинного обучения для прогнозирования VTEC

Обозначим основные шаги в фильтрации Калмана. Мы хотим учесть дополнительно предсказанное алгоритмом машинного обучения значение VTEC. Для этого в фильтр Калмана нужно включить его как часть состояния системы и использовать в моделировании динамики и измерений.

Включим расчетное значение VTEC как одну из переменных состояния и VTECpred (предсказанное алгоритмом машинного обучения) – как другую в векторе состояния. В качестве начального приближения для следующего шага будем использовать предсказанное значение VTEC.

Производим инициализацию матрицы измерений: x 0 =

- начальное состоя-

ние.

Перед каждым шагом прогноза необходимо обновить состояние внешним предсказа-

VTEC(pkre)d нием: xik ^ предыдущая_скорость

где i – номер столбца матрицы измерений x .

предыдущее_ускорение

Л t — Л t²

1      Л t

L                            J 1

Инициализация матрицы динамики: F = 0

Эта матрица моделирует эволюцию системы с учетом равномерного ускорения: первая строка – позиция обновляется с учетом скорости и ускорения, вторая – скорость обновляется с учетом ускорения, третья – ускорение предполагается постоянным. Матрица описывает, как VTEC изменяется со временем, например, с учетом предсказанного значения. Это классическая модель для системы с постоянным ускорением, где Δ t – дискретный шаг времени. В нашем случае он будет рассчитываться как разность между опорным временем (временем начала измерений) и временем текущего наблюдения.

Инициализация матрицы наблюдения: H =

Эта матрица связывает состояние системы с двумя источниками измерений – измерением VTEC и внешним предсказанием VTEC.

Далее для каждого шага времени k = 1,2, …, N .

Предсказание состояния: x _k^_k = Fx _k _ —_k - 1 + u _k . На этом шаге происходит прогноз следующего состояния системы с использованием модели динамики и предыдущего состояния, а также добавляется внешнее воздействие uk .

Предсказание ковариационной матрицы ошибок: P _k^ _ 1 = FP _k _ —_k _ 1 F T + Q .

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

Это обновление оценки неопределенности системы после прогноза, учитывающее модельный шум Q .

^VTECmeas , k

^VTECext _ pred , k

Получение измерений: z k =

.

На этом шаге получаем два источника данных: реальное измерение VTEC и внешнее предсказание VTEC, которые будут использованы для обновления.

Предсказание измерений: z kk _ 1 = HX kk _ 1 .

На этом шаге происходит расчет ожидаемых измерений на основе прогнозируемого состояния с использованием матрицы наблюдения H – это функция измерения, связывающая состояние с наблюдаемыми данными.

Вычисление инновационной ковариационной матрицы: S _k = HP k । _k _ 1 H T + R .

Обновление: после получения новых измерений необходимо скорректировать предсказанное значение VTEC с помощью фильтра Калмана, чтобы получить более точную оценку.

Расчет коэффициента Калмана: K _k = P _k।_k _ 1 H T S ^_ .

Этот коэффициент определяет, насколько сильно обновлять состояние, учитывая ошибку измерений и неопределенность модели.

Обновление оценки состояния: x k । k = x k । k _ i + K_k ( z k ^_ z k । k _ i ) .

Это шаг, в котором прогнозируемое состояние корректируется на основе разницы между фактическими измерениями и их предсказаниями, умноженной на коэффициент Калмана. Этот шаг позволяет системе учитывать новые данные и уменьшать неопределенность оценки.

Обновление ковариационной матрицы ошибок: P kik = ( I _ K _k H ) P _k\_k _ 1 .

Проведем моделирование алгоритма. Оно нам позволит получить численный и графический результат. Получившуюся характеристику представим на Рисунке 1. На рисунке видно, каким образом в результирующем графике учитывается последовательность значений внешнего предсказания.

Для формирования локальной модели была разработана подпрограмма расчета, основанная на алгоритме, описанном в п. 1. Она написана на языке программирования С++, так как алгоритм накопления измерений работает в микроконтроллерном навигационном устройстве. Все основные математические функции для расчета ионосферных моделей сведены в класс ION. Опишем структуру программы, используя язык программирования.

При старте программы осуществляется вызов функции ION::InitIonoMode (intperiod) , которая применяется для старта. В качестве параметра ей передается период, в течение которого будет происходить наблюдение и запись результатов навигационных измерений. Данный параметр задается в настройках навигационного приемника.

Дальнейшая работа программы проходит внутри функции voidION::IonoProc() . Сначала происходит считывание значения времени из структуры, заполняемой при приеме данных от приемника, проверка его корректности. Далее при первом запуске происходит создание структуры станции мониторинга ионосферы для данного приемника:

St0 = new STATION(nChan), где STATION – дружественный ION класс , nChan – номер канала (антенны).

Предсказание и уточнение ионосферных поправок в радионавигации на основе машинного обучения и фильтра Калмана с использованием данных...

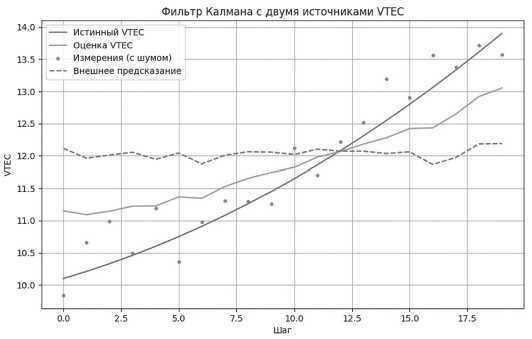
Рисунок 1. Характеристика фильтрации Калмана с двумя источниками VTEC Источник: здесь и далее рисунки выполнены автором.

Осуществляется вызов функции StartNavDataPeriod(tep) для текущего момента времени tep , в которой фиксируется текущее время как время начала наблюдений, обнуляются маски наличия спутников по всем системам. Дальнейшие вызовы функций происходят уже в постоянном режиме. Происходит инициализация координат приемника для станции мониторинга:

St0->InitPecef();

Вызов функции измерений:

St0->MeasChan(tep);

В ней происходит запись измеренных значений L (фаза несущей частоты), C (измеренная псевдодальность), D (измеренный доплер) в структуру OBSDATA , созданную для каждого спутника. Данные значения получаются посредством функции GetIonoLCD() , которая обеспечивает их получение из данных, полученных из приемника при его периодическом опросе. Далее в процедуре обработки новой обсервации void STATION::Meas Processing(constOBSDATA&Obs) происходит запись данной обсервации в список сеансов измерений для данного спутника. Для этого используется OBSDATA – это структура данных по одному спутнику за одну эпоху (но по обеим частотам). Из набора этих структур по всем спутникам создается массив Iep[nsys][NSat] . Элемент массива – список сеансов измерений для одного спутника:

ISEANSseans(Obs,Interval);

std::list&iepList = Iep[nsys][NSat];

где

ISEANS – класс, который определяет интервал, на котором производится непрерывная оценка параметров ионосферы;

Interval – дискретность измерений в сек.

Далее обрабатываются последующие измерения при помощи добавления их функцией AddObservation(Obs) , где nsys – номер навигационной системы; nSat – номер спутника.

В функции обработки обсервации boolISEANS::AddObservation(const OBSDATA& Obs) проверяются выполнения условий допустимости значений измерений C, D, L и происхо-

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

дит их интегрирование по одной или двум частотам в структуре накопления АСС . Если условие не выполнено, то измерение идентифицируется как сбойное и происходит сброс интегратора. Вычисляется линейная комбинация одночастотных измерений:

Z = (ACC.C1 - ACC.L1* C/FreqL1 )/(2.0*dTacc), а если измерения двухчастотные, составляем двухчастотную комбинацию:

Z = - C*(ACC.L1/FreqL1 - ACC.L2/FreqL2)/((1-sqr_freq12)*dTacc), где dTacc – время накопления измерений;

FreqL1, FreqL2 – первая и вторая несущая частота измерений;

sqr_freq12 – квадрат отношения F1/F2 .

Это Z и будет являться оценкой TEC. TEC – это наклонная электронная концентрация, которая определяется вдоль направления на спутник, измерения которого используются. VTEC определяется через нее так: VTEC = TEC/FZ, где FZ – функция наклона, пропорциональная высоте спутника [1]. Вычисление TEC далее описано через коэффициенты разложения локальной модели ионосферы.

Далее производится проверка на возможный срыв слежения или выброс, и если был срыв слежения, то происходит реинициализация фильтра Калмана, и измерения обрабатываются в алгоритме фильтрации Калмана, в которой участвуют следующие параметры:

Const double **F – матрица прогноза.

Матрица наблюдений определяется как

Const double H[Nsrc][SIZE_VIP] = {{1,0,0}{1,0,0}}; // матрица наблюдений (частных производных), где

Nsrc = 2 – это число источников данных. У нас их два (от радионавигационных измерений и предсказанное алгоритмом машинного обучения);

SIZE_VIP = 3 – размерность матрицы процесса (оценка TEC, скорость TEC и скорость изменения TEC);

R – дисперсия оценки.

Для инициализации точек прокола организован цикл по списку NavDataList , в котором в функции boolSTATION::NewIPoint(const NAVDATA *SV) в каждую точку прокола из списка всех точек прокола ионосферы заносятся следующие вычисленные значения из NavDataList , где параметр SV – вектор состояния спутника:

Ipp.push_back(IPPIERCE(SV->Id,Isf,Vsf,FZ,TEC,RMS));

Vsf – скорость перемещения подыоносферной точки;

Igg – географические координаты подыоносферной точки;

Isf – координаты подыоносферной точки в фиксированной относительно Солнца системе координат;

Angle – трехмерный угол направления на спутник;

FZ – фактор угла наклона;

RMS – среднеквадратическое отклонение.

Первоначальное приближение TEC в параметрах функции вычисляется как прогноз значения на момент Т через начальные значения коэффициентов фильтра Калмана как TEC = Xkalm[0] + dt*Xkalm[1] , где dt – промежуток времени с момента последней обсервации. Далее вызывается процедура создания новой точки прокола, где создаем узлы

Предсказание и уточнение ионосферных поправок в радионавигации на основе машинного обучения и фильтра Калмана с использованием данных...

в списке точек прокола ионосферы ListNode . При этом идет цикл от минимальной долготы FirstLon до максимальной LastLon с шагом 5º. FirstLon и LastLon определяются через FirstObs и LastObs соответственно при подстановке их в функцию SunFixCoorIp() . В функции SunFixCoorIp() к значению долготы в градусах прибавляется текущее время, переведенное в градусы.

FirstLon = SunFixCoorIp(St0->Pgeog,St0->FirstObs).lon;

LastLon = SunFixCoorIp(St0->Pgeog,St0->LastObs).lon;

где St0->Pgeog – географические координаты приемника.

После выполнения этих расчетов происходит вызов функции BuildLIM() для построения локальной модели ионосферы. Внутри этой функции строятся две модели разного порядка: lim1 (первого порядка) и lim2 (второго порядка). Проверяется условие того, что число принятых спутников не меньше достаточного количества для применения модели второго порядка. Если число спутников меньше 8, то понижаем порядок модели. Далее в цикле по всем подыоносферным точкам for(ipp = St0->Ipp.begin(); ipp != St0->Ipp.end(); ++ipp) {….} определяются квазиэкваториальные координаты и скорость точки прокола:

Здесь param3 – структура вида {X,Y,Z};

Далее для этих величин производится вычисление коэффициентов разложения локальной модели ионосферы в ряд Тейлора H[0]- H[5] по методу наименьших квадратов. Эта последовательность коэффициентов H идет в функцию фильтрации Калмана как строка частных производных параметра Z по оцениваемым параметрам.

Оценка TEC рассчитывается, таким образом, в соответствии с разложением Тейлора. Для порядка модели, равного 1:

if (Order == 1) {

F[] = {1,d.X,d.Y};

tec = Xkalm[0]+Xkalm[1]*F[1]+Xkalm[2]*F[2];

}

Для порядка модели, равного 2:

if (Order == 2) {

F[] = {1,d.X,d.Y,d.X*d.X,d.Y*d.Y,d.X*d.Y};

Tec= Xkalm[0] +Xkalm[1]*F[1]+ Xkalm[2]*F[2]+ Xkalm[3]*F[3]+ Xkalm[4] *F[4]+ Xkalm[5]*F[5];

}

Затем для заключительных этапов алгоритма TEC преобразуем в VTEC, как описано выше.

Далее считываем значение предсказанной алгоритмом машинного обучения оценки VTEC:

z_pred = GetTEC_FromBase(lon,lat, year, day, hour);

Здесь функция GetTEC_FromBase() считывает по заданным координатам широты, долготы, даты и времени значение VTEC из сформированного предварительно табличного файла на нужный промежуток времени и участок местности по работе алгоритма предсказания и машинного обучения [2].

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

В вектор измерений z записываем реальное + внешнее предсказание:

Z[]={Zm, z_pred};

Берем эти измерения Z и делаем фильтрацию по Калману:

Далее находим R (оценка дисперсии):

if (fSingleFreq) { // признак одночастотных измерений (по частоте L1)

interval = (Interval > 1)?Interval:1;

R = (rms_code)*(rms_code)/(4.0*(dTacc/(interval)));

}else {

R = 4/((1-sqr_freq12)*(1.-sqr_freq12))*(rms_phase)*(rms_phase)/(dTacc/(Interval));

}

Далее осуществляется фильтрация Калмана:

Forecast(F).Filtr(Z,H,R);

Результатом будет Xkalm[0],Xkalm[1].

Xkalm[0] перед следующим шагом присваиваем значение Z[0] , то есть это и есть искомая оценка VTEC. Для вычисления более точного значения можно применять формулы разложения локальной ионосферной модели в ряд Тейлора, используя модель первого или второго порядка [1]. Там будут использоваться приращения dX и dY по сетке квазиэквато-риальных координат и, соответственно, значения Xkalm[0],Xkalm[1] и Xkalm[2] .

Результаты работы

В результате мы получим распределение VTEC в виде географической карты по широте и долготе. Мы ее можем получить при помощи составления глобальной модели ионосферы (GIM) и передать из навигационного контроллера через интерфейс связи с внешним компьютером, используя специально разработанный протокол и информационные пакеты данных, так как мы это делали в работе [1], а на компьютере уже построить карты распределения VTEC.

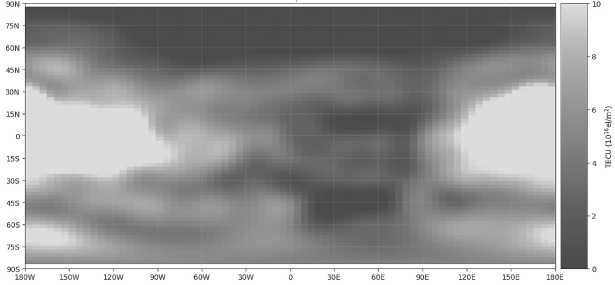
Рисунок 2. Карта распределения ионосферной электронной концентрации VTEC земной поверхности

Теперь мы можем скачать с сайта glonass-iac карту VTEC на выбранную дату и время и принять ее как эталонную для сравнения [2]. Далее вырезаем из этих обеих глобальных

Предсказание и уточнение ионосферных поправок в радионавигации на основе машинного обучения и фильтра Калмана с использованием данных...

карт наш локальный участок местности, на котором проводилась обработка спутниковых измерений. Этот участок будет ограничен линиями по широте FirstLat , LastLat и долготе FirstLon , LastLon . Затем вычисляется корреляцию между этими двумя изображениями с использованием функции библиотеки numpy и ssim. Скачаем карты распределения VTEC для дат 15-03-2023 и 15-08-2023. Проведем расчеты для сравнения для пяти разных географических районов:

• #    grid_lat, grid_lon – двумерные массивы координат

• #    VTEC_origin_1, VTEC_res_1 – эталонная и сформированная по измерениям карты для первой даты

• #    VTEC_origin_2, VTEC_res_2 – эталонная и сформированная по измерениям карты для второй даты

• #    Создаем координатные сетки

latitudes = np.linspace(-90, 90, 180)

longitudes = np.linspace(-180, 180, 360)

grid_lat, grid_lon = np.meshgrid(latitudes, longitudes, indexing=’ij’)

• #    районы для анализа

districts = [

{‘FirstLat’: -30.0, ‘LastLat’: 0.0, ‘FirstLon’: -60.0, ‘LastLon’: 0.0},

{‘FirstLat’: 30.0, ‘LastLat’: 60.0, ‘FirstLon’: 60.0, ‘LastLon’: 120.0},

{‘FirstLat’: -60.0, ‘LastLat’: -30.0, ‘FirstLon’: 120.0, ‘LastLon’: 180.0},

{‘FirstLat’: 40.0, ‘LastLat’: 45.0, ‘FirstLon’: -10.0, ‘LastLon’: 10.0},

{‘FirstLat’: -45.0, ‘LastLat’: -40.0, ‘FirstLon’: -120.0, ‘LastLon’: -115.0},

]

correlation_results = []

for idx, district in enumerate(districts):

FirstLat = district[‘FirstLat’]

LastLat = district[‘LastLat’]

FirstLon = district[‘FirstLon

LastLon = district[‘LastLon’]

• #    Создаем маски по координатам

• #    Вырезаем области

VTEC_origin_crop_1 = VTEC_origin_1[region_mask]

VTEC_res_crop_1 = VTEC_res_1[region_mask]

VTEC_origin_crop_2 = VTEC_origin_2[region_mask]

VTEC_res_crop_2 = VTEC_res_2[region_mask]

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

• #    вычисляем корреляцию методом SSIM

ssim_score_1 = ssim(VTEC_res_crop_1, VTEC_origin_crop_1)

ssim_score_2 = ssim(VTEC_res_crop_2, VTEC_origin_crop_2)

Результаты корреляции всех вариантов сравнения карт мы получили в диапазоне 0,78…0,9. Это достаточно хороший результат, который показывает точность прогнозирования VTEC при помощи нашего метода.

Заключение

В данной статье предложен комплексный подход к предсказанию и уточнению ионосферных поправок в радионавигации, основанный на использовании методов машинного обучения и фильтра Калмана. Объединение предсказанных значений электронной концентрации, полученных с помощью моделей и алгоритмов машинного обучения, с реальными радионавигационными измерениями позволяет значительно повысить точность и оперативность оценки ионосферных эффектов. Проведенные эксперименты подтвердили эффективность предложенного метода, что делает его перспективным для внедрения в современные навигационные системы, обеспечивая более надежную и точную работу в условиях изменяющейся ионосферной среды.