Представление формулами Фейнмана полугрупп, порожденных параболическими дифференциально-разностными операторами

В настоящей работе исследуются вопросы корректной разрешимости задачи Коши для модельного параболического дифференциально-разностного уравнения вида.

N

• u_t(x, t) = Au(x, t) + У^ ak(u(x — hk , t) + u(x + hk , t)), (x, t) E R x R₊,         (1)

г=1

дополненного начальным условием

u(x, 0) = ug(x), x E R.                                    (2)

Здесь uo - заданная функция, hi,..., hk - полижи тельные и ak, к E 1,..., N - вещественные числа.

Уравнения указанного вида, возникают при описании явлений диффузии или теплопроводности в которых возникают источники, нелокально зависящие от состояния (т.е. от плотности распределения концентрации или температуры) и. В частности, уравнения вида (1) возникают при исследовании задач управления явлениями теплопередачи, в которых динамика состояния и задается дифференциальным уравнением:

ut(x, t) = Au(x, t) + g(t, x, и), (x, t) E R x R+, с управлением g в случае, когда, управление g задается действием на. состояние u операторов отклонения аргумента в композиции с операторами дифференцирования и умножения на функцию (см. [1], [2], [3]).

В работе определено представление полугруппы решений задачи Коши для функционально-дифференциального уравнения посредством формулы Фейнмана, (см. [4]). Это означает, что хотя представление эволюционного оператора, задачи Коши (1) можно определить только в терминах спектрального разложения (в простейшей ситуации -в терминах преобразования Фурье решения), тем не менее мы получаем аппроксимацию эволюционного оператора последовательностью n-кратных композиций интегральных операторов, ядрами которых являются элементарные функции.

В терминах, сформулированных в монографии [1], дифференциально-разностное уравнение (1) относится к типу смешанных дифференциально-разностных уравнений без отклонения по времени. Нелинейные параболические дифференциально-разностные уравнения возникают при исследовании нелинейных оптических систем с обратной связвю (см. [3]). В работе [5] сформулированна постановка смешанной задачи для нелинейного параболического дифференциалвно-разностного уравнения и установлено, какие свойства отличают указанную задачу от смешанной задачи для параболического дифференциальное уравнения. Рассматриваемая нами линейная задача Коши (1), (2) может быть рассмотрена как линеаризация указанных нелинейных смешанных задач.

Аппроксимация полугруппы операторов, порожденной задачей Коши для уравнения теплопроводности с отклоняющимся аргументом, формулами Фейнмана позволяет не только выразить решение задачи Коши с помощью конструктивных алгоритмов, но и исследовать вероятностную структуру явлений отклонения аргументов в уравнении теплопроводности, поскольку формулы Фейнмана определяют марковский случайный процесс, математическими ожиданиями функционалов от которого являются решения задачи Коши.

2.    О корректной разрешимости задачи Коши и связанной с ней полугруппе операторов

Поставим задачу определить решение уравнения (1), удовлетворяющее начальному условию

n(x, 0) = ng(x), ж G R.                                    (2)

Определение 1. Сильным решением задачи Коши (1), (2) назовем функцию n G С ([0, +то), W^(R)) QC¹((0, + to ),L ₂ (R)), которая удовлетворяет уравнению (1) и условию (2). Функцию n G С ([0, + to ),L 2 (R)) назовем слабым решением задачи Коши (1), (2), если существует такая последовательность начальных данных {ngk}, которая сходится в пространстве Н к элементу ng, такая, что при каждрм к G N существует сильное решение nk задачи Коши с начальным условием ngk и последовательность функций сходится к функции n в пространство С ([0, +^),L2(R?)Y

Заметим, что как сильное, так и слабое решение удовлетворяют уравнению (1) и условию (2) в смысле интегрального тождества.

Предположим, что существует решение n(x,t), t > 0, x G R, задачи Коши (1), (2). Чтобы найти представление решения задачи Коши (1), (2) через начальное условие, применим преобразование Фурье F к левой и правой частям уравнения (1):

N

F{nt(x, t)} = F {An(x, t)} + ^ F{ak(n(x — hk, t) + n(x + hk , t))}.           (3)

г=1

Пусть функция U (s,t), s G R, t G (0, +то) является преобразованием фурье-функции n(x,t) по первой переменной. Тогда уравнение (3) обретает вид: U_t(s,t) = —s²U(s,t) + E^k U (s, t) exp(ishk) + U(s, t) exp(— ishk )), а начальное условие (2) - вид U (s, 0) = U_g(s) = F (n_g)(s), s G R.

Тогда с помощью преобразований

Ut(s, t) = —s^U (s, t) + ^=1 ak(exp(ishk ) + exp(—ishk))U (s, t),

T^t) = —s² + EhL ak(—is exp(ishk) — is exp(—ishk )) = — s² + 2 ^^ ak cos(shk),

Rg w8^d^ = Rg^(—s2 ^{+ 2} ^^N=1 ^ak cos^(shk Ж,

InU(s,()|g = (—s2 + 2 ^N=1 ak cos(shk))C|g, ln U(s, t) — In U(s, 0) = (—s2 + 2 ^^=1 ak cos(shk))t получаем, что

N

и(s,t) = Uо(s) exp [(—s² + 2 ^ ak cos(shk ))t].                      (4)

г=1

Таким образом, установлено следующее утверждение.

Замечание 1. Если задача Коши (1) - (2) имеет решение п, то фурье-образ U(s,t функции п определяется равенством (4).

Теорема 1. Формула (4) определяет сильно непрерывную полугруппу U (t), t > 0, преобразований пространства Ь2(Н)

Действительно, в силу унитарности преобразования Фурье в пространстве Н = L2(R) достаточно проверить, что однопараметрическое семейство операторов U(t), t > 0, умножения на функции U(s,t^,t Е R+, является полугруппой сильно непрерывных операторов в пространстве L2(R) с нормой не больше единицы. Полугрупповое свойство U(s,ti)U(s,t2) = U(s,ti + t2) следует из свойств экспоненциальной функции. Сильная непрерывность в точке t = 0 оператор-функции U(t), t > 0, следует из равномерной на любом отрезке числовой прямой сходимости функции U(s,t), t Е R+, s Е R, к единичной функции 1(s), s Е R, при t ^ 0. Тогда сильная непрергтвиость в любой точке t > 0 следует из полугруппового свойства. При этом тип ш полугруппы U(t), t > 0, равен величине N                                       N sup /(s), где /(s) = —s2 +2 £г=1 ak cos(shk), s Е R,n допускает оценку сверху ш < 2 £ lak|-seR                                                                                    '                   '          '           k=1

Теорема 1 доказана.

Теорема 2. Задача Коши (1), (2) имеет единственное обобщенное решение n(t), t > 0, которое определяется как действие полугруппы U(t), t > 0, на начальное условие по.

Согласно замечанию 1, если решение задачи Коши (1), (2) существует, то оно представимо в виде

N

п(х, t) = по(х) * F ^-1{exp [(—s² + 2 ^^ ak cos(shk))t]}.                   (5)

г=1

Наоборот, если функция U (s,t), s Е R,t > 0, определена равенством (4), то функция п, полученная с помощью обратного преобразования Фурье, является решением n(x,t) = F^-1{U (s,t)} задачи Коши (1). (2):

N

п(х, t) = по(х) * F ^-1{exp [(—s² + 2 ^^ ak cos(shk ))t]}. г=1

Действительно, поскольку для каждой функции Uо(s) Е L2(R), удовлетворяющей условию s2Uo(s) Е L2(R), функция U(s,t), определенная равенством (4), принадлежит пространству С([0, +to),L2(R))QC 1((0, +to),L2(R)), удовлетворяет включению s2U(s,t) Е С([0, +to),L2(R)) ii уравнению д N d^U(s,t) = (—s2 + 2^ ak cos(shk))U(s,t).

г=1

В силу унитарности преобразования Фурье для каждой начальной функции по Е W2(R) соответствующая функция (5) является сильным решением задачи Коши (1), (2). Следовательно, формула (5) определяет образ функции по Е W22(R) при действии операторов полугруппы U(t), t > 0. Поскольку в силу теоремы 1 полугруппа U(t) имеет ограниченный экспоненциальный рост ш, то тогда полугруппа U(t) допускает продолжение по непрерывности с пространства W2(R) на пространство L₂(R). И, следовательно, для любой начальной функции по Е L2(R) функция п(t) = U(t)по, t > 0, является обобщенным решением задачи Коши (1), (2). Теорема 2 доказана.

Следствие 1. Генератором полугруппы U (t), t >   0, является оператор

N

L = А+ £ ak(Sh_k + S-_hk ), где Sh - оператор сдвига (іргумспта па число h Е R. k=i

Полученное представление решения задачи Коши (1), (2) не является конструктивным. Для аппроксимации полученного решения с помощью последовательностей кратных интегралов от элементарных функций используем подход из работ [4], [6], [7], основанный на формулах Фейнмана.

3.    Черновские аппроксимации решений задачи Коши

Следуя подходу, предлагаемому в работе [4], определим операторнозначную фунцию, эквивалентную по Чернову полугруппе операторов U(t), t >  0. Теорема Чернова (см. [8]) утверждает следующее.

Пусть операторнозначная функция F(t), t > 0, со значениями в банаховом пространстве В (Н ) непрерывна в сильной операторной топологии, допускает оценку l|F(t) |в(п) < 1+at, t > 0, при некотором а >  0 и, кроме тог о, оператор F‘(0) замыкаем и его замыкание является генеретором сильно непрерывной полугруппы U(t),t > 0. Тогда для любого n Е Н и любого Т > 0 выполняется равенство lim sup ||U(t)n — (F(-)ⁿ п|я = 0.

ⁿ "^x te[G,T]

Следуя данному в [4] определению, операторнозначную функцию F(t), t > 0, будем называть эквивалентной по Чернову полугруппе U(t), t > 0, если для любого n Е Н выполняется равенство lim sup ||(F(—))nn — U(t)u|n = 0 n 'х [G,T]        П при любых Т > 0.

Для заданных в уравнении (1) параметров а и Һ рассмотрим операторнозначную функцию F_tt,h : R+ ^ В (Н ), определенную на полуоси R+ = [0, +то) и принимающую значения в банаховом пространстве В (Н ) ограниченных линейных операторов в гильбертовом пространстве Н . При каждом значении t > 0 определим ее значение Ғ_а,Ді) равенством

Fa,h(t)uG = n(t, ж) =

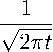
Г + ^

-∞

[exp(

— (ж — у)² 4t

)+

^+at(exp^{( ( Ж} ₄ ^у —) ^{+ ex}p^{( ( Ж} ₄ ^{у + Һ )} ))^|ио(у)^у

для произвольной функции u g из плотного в пространстве Н линейного многообразия D = CG°(R). Предлагаемый вид черновской аппроксимации полугруппы связан с тем, что первое слагаемое в формуле (6) соответствует динамике, порожденной невозмущенным уравнением теплопроводности, а второе и третье слагаемые при малых: значениях переменной t учитывают влияние смещенных источников.

Проверим условия теоремы Чернова для операторнозначной функции F_a,h(t), t Е R+. Лемма 1. Если ug Е D, mo значение производной ^ Ғ _а,Ді)ио нpu t = 0 равно

^^ Fa,A(t)nG|t=G =

д ²ug дж²

(ж) + а(по(ж + Һ) + по(ж — Һ)).

Для доказательства леммы вычислим функцию ( ^дН; — д'? )(t, ж), t > 0, ж Е R. Поскольку

(*) = -^ Z+”[exp(     ^ )+at(exp(—(Ж "( — Һ)2 )+exp(—(Ж "Д Һ)2 ))|«o(y)dV + dt z^ty 2^t —^         4t                    4t                   4t

1   Z⁺“ ^{( ж —} у^{)2     — ( ж —} у^{)2          — ( ж —} у - ^{Һ)2        — ( ж —} у ^{+ Һ)2}

+ V^ L .-     '4   )+ a(exp(----4t----)+eXp(----4t----» +

. ^{(ж — у — Һ)2}    (^{— ( ж — у — Һ)2 ( ж — у + Һ)2}    (^{— ( ж — у + Һ)}

+at(----42-----exp(------4t------)+----4t2-----exp(------4t------))|по(уду

и то

d ²u      1

dx2   V2xt

■ х -1

J-. [йexp(

-(x — у)² 4t

) + T exp( -)+

^-1    / ^{- (x - у - h)}x ^{(x - у - h)}

'   ,- exp*----- 4t -----) ⁺----4t^"

(x - у + h)²

+    4t2

,Эи   Э2их,

⁽ И ^- 85 ><‘-^x> =

2тт?

- exp(

exp(

Z'^(a exp

-∞

-

-Г-Х-У) - — exp( 4t        ’    2t

^{( X} ₄ ^{у + h} ЖМ

(x - у - h)²

+ a exp 4t

-

^(x - у + ^⁾² )+

4t )+

^{( x} ₄ ^{y + h ) )u}o⁽y^)dy.

Следовательно, d                        Э2и          ci C^

-(x - у - h)²

-----4t-----+eXp

^{( X} ₄ ^{y +} ^ ) ^)uo⁽У^)dУ^] =

dF“^(t’u»|-» = M85 (t-x)+ ... L (exp d2u0 , .       ,

= -rr^-(x) + a(uo(x + h) + Uo(x - h)).

ox2

Лемма 1 доказана.

Для заданных в уравнении (1) коэффициентов ak,hk , k Е 1,N определим оператор-функцию Fa,h (t), t > О, полагая, что для каждой функции ио Е D ее образ Fa,h (t)uo определяется равенством

1     '^      -(x - у)2х

^{F ah (i)}"^o(x) = ?S L       4   ⁾⁺

I ^       Г^ ^{- у - hk )2}^ I    ( ^{-(x - у + hk}

■ X ^akt(exp⁽ ------47------) ^{+ e}xp⁽------4т------^))]dу.

k=1

Следовательно, в силу леммы 1 на линейном многообразии D оператор ^ F a,h (t)|t=o совпадает с генератором полугруппы U(t), t > 0.

Докажем сильную непрерывность операторнозначной функции F a,h (t).

Лемма 2. Операторнозначная функция F a,h (t), t > 0, непрерывна в сильной операторной тополоии на полуоси t > Ом допускает оценку по норме ||Fa,h (?) Һ в ( н ) ^ 1 + 2at, t > 0.

Операторнозначная функция F _a,^ (t) является сум мой функции F o(t) с интегральным ядром уравнения теплопроводности и функции Ф _о,^(?) с интегральным ядром Ф a,h(t,x,у) = ^==^ [at(exp(-0^-j^l- )+exp(-(^-j^L))]. При чем Ф „,_һ(?) = at F o(t)( S _h+ S -_h), где S ±^ - операторы сдвига аргумента на величину ±h. Как известно, операторнозначная функция Fo(t),t > 0, непрерывна в сильной операторной топологии и равномерно ограничена в топологии нормы, а операторы S ±^ ограничены. Следовательно, операторнозначная функция Ф(і,Д?) непрерывна в сильной операторной топологии.

Докажем оценку нормы операторнозначной функции F_a ^ (t).

Операторнозначная функция F o(t) допускает оценку | F o(t)|_B(H) < 1, а функция Ф _а,к (t) - оценку | Ф_а ,л (?) | в ( н ) ^ 2at. Следовательно, справедлива оценка ||F_a ,h(t) | в ( н ) ^ 1 + 2at и выполняется последнее условие теоремы Чернова.

Таким образом, установлена следующая теорема.

Теорема 3. Оператоорнозначная функция F_a ,h(t), t > 0, эквивалентна по Чернову полугруппе U (t), t >  0.

Заключительные замечания. Установленный теоремой 3 результат позволяет задать аппроксимации решения задачи Коши (1), (2) последовательностью кратных интегралов, подынтегральное выражение которых содержит элементарные функции и начальное условие. Кроме того, полученные формулы Фейнмана:

U(t)uo($) =

Jim J J..   ‘

R R R

— tN -1, Ж, yN-1)F_a,_h(tN -1

^{— t}N -2,yN-1,yN -2) —

Наоборот, если на алгебре Л цилиндрических множеств в пространстве С(R+, R) непрерывных отображение временной полуоси [0, +то) в координатное пространство R задана марковская квазимера ц (см. [10], [11]), значение которой на произвольном цилиндрическом множестве А = Д € С (R+,R) : ДД ) E Bj , j E 1,п, где Bj - ограниченные множества из алгебры B(R) борелевских подмножеств в R, п = 2, 3,... и 0 <  t1 < t₂< ... < t_n, задается равенством (см. [13])

Ц^(А) = ⁽ХВ„ , ^U(tn ^{- t}n-1^)PB„—i^U(tn-1 ^{- t}n-2⁾...U^(t3 ^{- t}2^)PB2^U(t2 ^{- t}1⁾XBi)b₂(R)    ⁽⁸⁾

(здесь х в ~ характеристическая функция множества B, а Р в - проекционный оператор умножения на характеристическую функцию множества B), то тогда справедлива следующая формула Фейнмана—Каца:

( х в ,и(^ =   j    х в (£(t)No(£(O))d/z(x), V t> 0, B E B(R),

C(R+,R)

однозначно определяющая решение n задачи Коши (1), (2). В приведенном выше равенстве интеграл понимается как интеграл от функции, аппроксимируемой линейными комбинациями индикаторных функций цилиндрических множеств, по конечно аддитивной мере, заданной на алгебре Л.

Заметим, что исследованию мер, подобных мере (8), и получению с их помощью представлений решения задачи Коши для уравнения Шредингера или уравнения Дирака посвящена работа [12]. В указанной статье (псевдо) мера определяется с помощью процедуры специального произведения переходных амплитуд. Предлагаемое в (8) задание меры с помощью произведения операторов является, по-видимому, эквивалентным представлением произведения переходных амплитуд, но проверка высказываемого предположения является темой дополнительного исследования.

Авторы благодарят за поддержку РФФИ, гранты № 09-01-00265 и № 10-01-00395.