Представление и обработка образов конструктивных элементов

На многих современных предприятиях используются системы автоматизированного проектирования (САПР). САПР – системы автоматизированного проектирования, использующие различные графические ядра для построения геометрии. В настоящее время основной проблемой, с которой сталкиваются группы разработчиков, является отсутствие возможности полноценного обмена результатами проектной деятельности при использовании различных систем автоматизированного проектирования. Их работу регламентирует стандарт ISO 10303 STEP (STEP - Standard for the Exchange of Product Model Data), который позволяет осуществлять обмен конечными решениями, но без возможности редактирования. [6]

Данную проблему устранила бы возможность восстановления способа построения экспортируемого объекта.

Для решения данной задачи было поставлено целью разработать модель, которая позволяла бы в полной мере описывать способ построения конструктивного элемента. Для реализации геометрической части модели были использованы библиотеки открытого графического ядра OpenCASCADE, подключенные к интегрируемой среде разработки Mirosoft Visual Studio, в качестве конструктивного элемента выбран фасонный резец. Как математическое ядро модели была рассмотрена теория графов, конкретно И/ИЛИ графы, структура которых полностью подходит для полного описания дерева построения конструктивного элемента. [1][3]

Концепция реализуемой модели представлена на Рисунке 1.

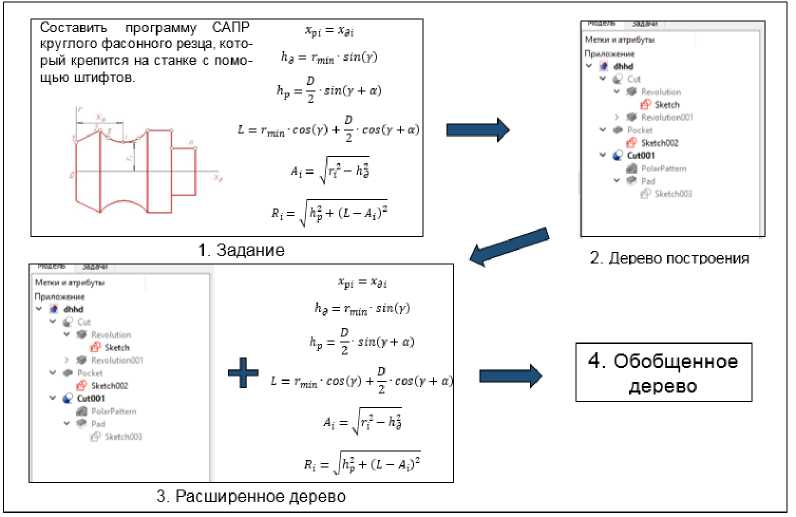
Рис. 1. Концепция модели

Шаг 1. Задание:

То, что имеется изначально - текстовое условие (сформулированная задача, говорящая, что нужно построить, с какими-либо ограничениями, например, формульными).

Шаг 2. Дерево построения:

На данном шаге производится геометрическая реализация задания: с помощью геометрических примитивов и операций над ними строится объект; реализуется дерево построения.

Шаг 3. Расширенное дерево:

На данном шаге задача - добавить в модель другие операции помимо геометрических. Назовем это расширенным деревом, помимо геометрии оно будет содержать в себе конструктивные особенности объекта, которые могут быть заданы формульно или, например, таблично.

Шаг 4. Обобщенное дерево:

Заключением построения модели будет являться обобщенное дерево – дерево, содержащее все возможные варианты построения конструктивного элемента.

Реализация такого рода модели с выполнением всех перечисленных шагов позволит получить полное описание конструктивного элемента со всеми его вариациями и способами построения. [2][4][5]

В ходе описания представленной модели были введены два новых понятия: расширенное и обобщенное дерево.

Принципиальное отличие обобщенного дерева от обычного дерева построения в том, что оно содержит в себе не только лишь геометрические особенности конструктивного элемента, появляющиеся естественным образом в процессе построения, но также и ограничения, несущие в себе принципиальные конструктивные особенности.

Рассматривая данные деревья с точки зрения теории графов можно сказать, что дерево построения - это ацикличное дерево без ветвления с последовательно соединяющимися вершинами (Рис. 2.).

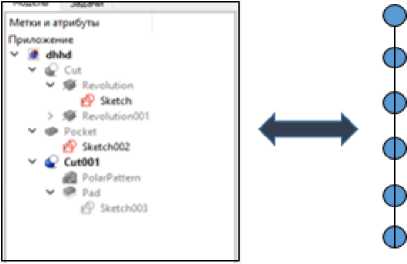
Рис. 2. Дерево построения

Расширенное же дерево – это уже дерево с ветвлением. Вершины, в которых происходит ветвление – вершины с выбором, которые и содержат в себе те самые конструктивные особенности (Рис. 3.).

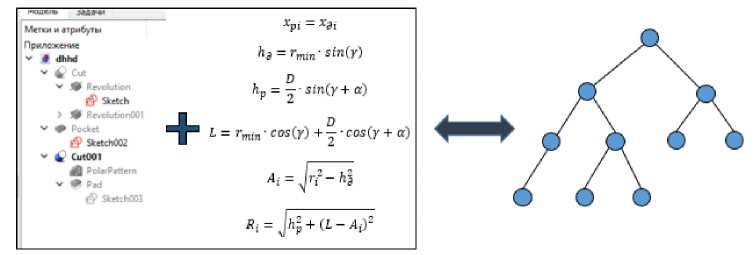
Рис. 3. Расширенное дерево

Обобщенное дерево дополняет расширенное тем, что содержит в себе помимо множества действий, необходимых для построения конструктивного элемента, также и конкретные пути решения, которые отражают алгоритм действий, после последовательного выполнения которых, получался конструктивный элемент конкретного вида.

Эти пути должны фиксируются с той целью, чтобы разработчик мог их идентифицировать. На обобщенном дереве построения решающие деревья выделены жирным (Рис. 4.).

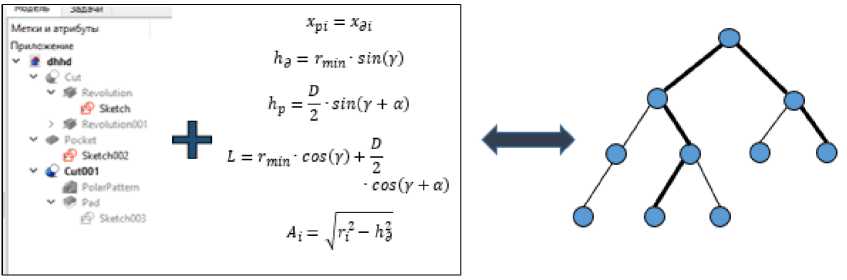
Рис. 4. Обобщенное дерево

Применительно к фасонному резцу, используемому для рассмотрения модели, выбор различных решающих деревьев может привести к построению круглого или призматического резца, что имеет принципиальную разницу для его использования на станках с различными креплениями. Однако оба способа получения должны быть отражены в модели, так как являются альтернативами одного конструктивного элемента (Рис. 5).

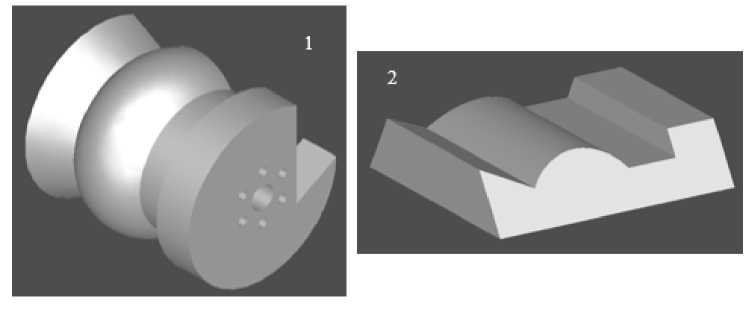
Рис. 5. 1 – круглый фасонный резец; 2 - призматический

Помимо концептуального представления, было разработано формульное описание, которое на конкретном примере фасонного резца демонстрирует возможность реализации представленной модели.

Для фасонного резца получен И/ИЛИ граф с решающими деревьями (Рис. 6).

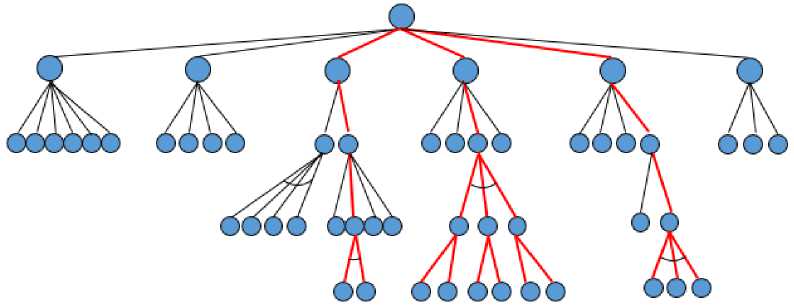
Рис 6. И/ИЛИ граф фасонного резца

Абстрактная формула (1) описывает геометрию построения (на Рисунке 7 представлены пояснения к переменным формулы (1)):

[( A v Bp ) v [( B v Bp ) v ( C v Bp )] v ( D v Bp ) v ( E v Bp ) v

v [( F v Bp ) л ( H v Bm ) v 6 л ( G v Bp ) л ( I v Bm )]] v ( J v Bm )

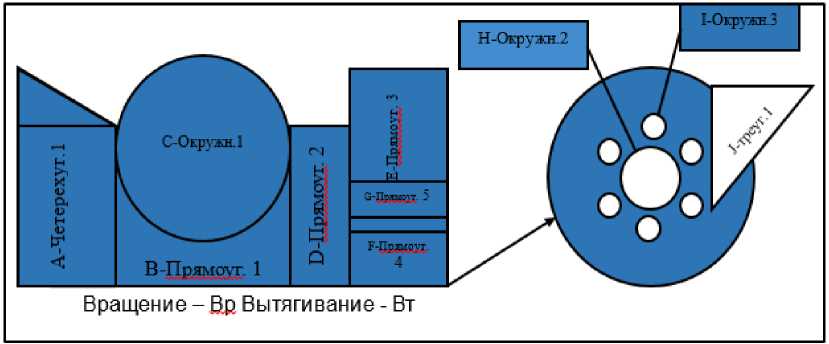
Рис.7. Описательная схема фасонного резца для получения абстрактной формулы

Формула (2) вводит в модель формульные ограничения:

Хл(rmin * sin YiV hs

D

D^                        D,

— * sm( Y i + ^a i ) ^л r min * cos Y i + у * co

¹ ^.+ «. ) ^л^

h pi

L i

r2 - hs л

A i

^л V h pi ^{+ ( L}i — ^{A ) 2}

R i

В формуле (2) векторы Yt , a i , D i , r i - векторы значений, определяемые для каждого конкретного фасонного резца индивидуально из таблиц технического задания (Приложение 1).

Векторы h§_t , h pi , L i , A i - векторы промежуточных расчетных значений.

Векторы Xi, R i - результирующие векторы значений, определяющих основные параметры фасонного резца.

А объединение формул (1) и (2) в систему (3) позволяет получить в полной мере описанный конструктивный элемент с геометрической и параметрической точки зрения.

[( A v Bp ) v [( B v Bp ) v ( C v Bp )] v ( D v Bp ) v ( E v Bp ) v

v [(F v Bp) л (H v Bm) v 6 л(G v Bp) л (I v Bm)]] v (J v Bm)

Xi ^{л (} r min * sin Y i )

hS

Di . • .

^л     * ^sin( Y i ^{+ a} i ) ^л r m

min

^h 5 i

Ai

^л ^h pi + ⁽ Li

R i

—

hpi

A i )²

D.

* cos Y i +    * cos( Y i + a i ) л

L i

Таким образом разработана модель, позволяющая в полной мере описывать способ построения конструктивного элемента, учитывая все аспекты построения: геометрию, конструктивные особенности в их математическом представлении (формулы, таблицы данных и т. д.) и множество путей решений получения различных образов одного конструктивного элемента.

При помощи разработанной модели был полностью описан процесс построения фасонного резца. Отмечены все его конструктивные особенности и все пути построения, что свидетельствует о пригодности полученной модели.

Полученная модель рассматривается как алгоритм для написания программного обеспечения, позволяющего осуществить автоматическую реализацию концепции модели при подключении к специализированным средствам (САПР).