Представление и отбор ситуаций на сложном технологическом объекте в условиях неопределенности

Вводные замечания

В целях безопасности и устойчивого функционирования систем критической инфраструктуры (системы обеспечения в городе, на месторождениях, на производстве и др.) актуальны задачи создания интеллектуальных систем поддержки принятия решений (ИСППР) для разработки оперативных программ действий персонала в аварийных или иных опасных ситуациях.

Одним из перспективных методов для разработки ИСППР при возникновении опасных ситуаций на сложных технологических объектах является метод вывода по прецедентам – case-based reasoning (CBR) [1, 4, 5]. Метод CBR позволяет создавать интеллектуальные системы, которые способны предлагать решения в опасных, нештатных ситуациях, делая это на основе имеющихся примеров – прецедентов, которые хранятся в базе знаний (БЗ). Каждый прецедент представляет собой пару <Ситуация, Решение>,

* Исследование выполнено при финансовой поддержке РФФИ и Тюменской области в рамках научного проекта № 20-47-720004.

Информационные технологии и оптимизация управления

с--------------------------------------------------------------------------------------------------------------

Глухих Игорь Николаевич доктор технических наук, профессор, заведующий кафедрой информационных систем Тюменского государственного университета. Сфера научных интересов: системы поддержки принятия решений, вывод решений на основе прецедентов, метод ситуационного управления сложными объектами, цифровые платформы, системная инженерия. Автор более 150 опубликованных научных работ.

то есть содержит описание ситуации и решения, которое для этой ситуации рекомендовано экспертами или было известно из практики.

Общий цикл вывода на основе прецедентов состоит из следующих этапов:

• •    идентификация текущей ситуации (ТС);

• •    поиск в БЗ такой ситуации Sit *, которая отвечает заданным критериям близости к ТС;

• •    вывод решения Sol *, ассоциированного в БЗ с Sit *;

• •    если найденная Sit * признана недостаточно близкой к ТС, то Sol * используют справочно как основу для разработки нового решения для ТС. Это новое решение впоследствии заносится в БЗ вместе с ТС. Так осуществляется пополнение текущих знаний системы по мере ее эксплуатации.

Практически важно, что первоначальное заполнение БЗ может быть выполнено с помощью экспертов на основе небольшого числа известных типовых ситуаций или их классов. Далее база знаний может пополняться в ходе эксплуатации системы.

Реализация CBR-системы предполагает разработку моделей для формализации представления ситуаций и отбора близких ситуаций в базе знаний.

В данной работе эти задачи решаются применительно к сложному технологическому объекту, который представляется с помощью четверки [6]

< O , S , R , A >,

Представление и отбор ситуаций на сложном технологическом объекте...

где O – множество из N элементов сложного объекта, которые могут взаимодействовать между собой; S – множество из n состояний, в которых могут находиться элементы объекта; R – множество отношений (связей) между объектами; A – множество аксиом, в частности, установленных приоритетов между элементами объекта и отношений между ними.

Такой сложный технологический объект появляется, например, в системах городской инфраструктуры (системы тепло-, водо-, энерго-, газоснабжения). В сложном технологическом объекте при устранении опасных, аварийных ситуаций для выбора действий нужно учитывать как состояние технологического оборудования, так и устройства технического обеспечения, интерфейсы с другими системами, внешнее окружение, наличие и состояние организационных элементов (обслуживающий персонал, ремонтные бригады и др.), а также климатические условия. Эта необходимость для принятия решений отражается в модели (1) включением в нее соответствующих элементов [6].

Ситуация, которая возникает на сложном объекте, рассматривается как сложившееся положение дел, которое характеризуется имеющимися на данный момент состояниями элементов объекта и отношениями между ними. Таким образом, на основе (1) можно сформулировать описание z- й ситуации следующим образом:

Sit_z = < O_z , S_z , R_z >,                                    (2)

где O_z ⊆ O – подмножество элементов, участвующих в данной ситуации; S_z ⊆ S – состояния, в которых находятся эти элементы; Rz ⊆ R – отношения между элементами в этой ситуации.

Тогда ситуационная база знаний (база прецедентов) задается как набор пар <Ситуация, Решение>:

CB = {< Sit_z , Sol_z | z = 1, 2, 3, …}.                            (3)

где решение Sol образуется из следующих основных элементов:

• •    инструкции по выполнению программы действий и рекомендации;

• •    нормативные и справочные документы, включая ссылки на подобные случаи (кейсы) в прошлом;

• •    адресаты – исполнители и иные участники программы действий, которым направляется решение.

С учетом сказанного задача вывода решения в ИСППР с ситуационной базой знаний формулируется как задача отбора в БЗ Sit * такой, что:

Sit* = argmax z Sim ( Sit z , Sit act ) с выводом Sol * <^ Sit*,                (4)

где Sit_act – текущая ситуация; Sim (.) – выбранный критерий близости (схожести) ситуаций.

В предыдущем исследовании авторов [6] для формализации представления ситуаций предложено использовать матрицы отношений и состояний, а отбор в БЗ делать поэтапно с учетом сходства в пространстве отношений и сходства в пространстве состояний.

В данной работе в развитие этих результатов рассмотрено представление ситуаций на множестве состояний, в которых могут быть элементы объекта, в условиях неопределен-

Информационные технологии и оптимизация управления ности. В статье сначала дается определение матриц состояний и вводится операция сравнения матриц для двух ситуаций. Далее на этой основе разрабатывается нейросетевой компаратор и предлагается нейросетевая архитектура, которая применима для сравнения и отбора ситуаций на сложном технологическом объекте.

Формализация представлений и отбор ситуаций в условиях неопределенности

В работе [6] предполагалось, что по наблюдениям за элементами O_i сложного объекта можно сделать однозначный вывод, в каком состоянии S_j находится каждый из этих элементов. Однако в практических ситуациях часто возникает неопределенность, когда невозможно сделать однозначный вывод о распознавании того или иного состояния. Для вывода в условиях неопределенности предлагается следующее обобщение представления ситуаций с помощью матриц.

Пусть сравниваются две ситуации: Sit_z – ситуация из БЗ, Sit_act – текущая ситуация на сложном технологическом объекте. Представлением ситуаций будут матрицы M1 и M2 соответственно. Число строк в матрице равно числу элементов сложного объекта из множества O , а число столбцов – числу состояний из множества S .

В условиях неопределенности на пересечении i -й строки и j -го столбца установлено значение ^ е [0,1] - значение функции принадлежности i-го элемента к j -му состоянию. В частном случае μ_ij может трактоваться как вероятностная оценка степени уверенности в том, что i -й элемент O_i находится в состоянии S_j .

На рисунке 1 приведен иллюстративный пример матриц для двух сравниваемых ситуаций (здесь пустые клетки означают заполнение их нулями), где есть четыре элемента объекта и четыре возможных состояния, в которых они могут находиться. Видно, что ситуации отличаются элементом О ₃, относительно которого сделаны разные выводы о его состоянии.

Ml О Sitz                   М2 ^ Sitact

	S1	s2	S3	s4
О1		0,3		0,7
О2	0,2	0,5	0,3
Оз				1
04	0,1		0,9

	Si	s2	S3	s4
О1		0,3		0,7
О2	0,2	0,5	0,3
Оз	0,2			0,8
О4	0,1		0,9

Результирующая матрица М = М1*М2

	S1	S2	S3	S4
Oi
О2
Оз	0,2			0,2
о4

Рис. 1. Матрицы сравниваемых ситуаций и результирующая матрица расстояний в пространстве состояний

Представление и отбор ситуаций на сложном технологическом объекте...

Результирующая матрица M = M1*M2, где * – операция вычисления расстояния dist между ячейками M1 _ij и M2 _ij этих матриц:

dist_ij = |M1 _ij – M2 _ij | =| µ _ij ^z – µ _ij ^act |.                                   (5)

Тогда для i -й строки матрицы можно вычислить расстояние dist_i между двумя ситуациями в пространстве состояний данного элемента O_i :

dist_i = min{1, ∑ dist_ij } и Sim_i = 1 – dist_i ,                           (6)

где Sim_i характеризует схожесть двух ситуаций в пространстве состояний по i -му элементу сложного объекта.

Итоговый показатель близости двух ситуаций Sim ( Sit_z , Sit_act ) вычисляется на основе свертки

Sim ( Sit_z , Sit_act ) = Σα _iSim_i ,                                  (7)

где α _i ∈ [0, 1], ∑ α _i = 1 – коэффициент относительной важности i -го элемента объекта при сравнении ситуаций.

Так, для ситуаций на рисунке 1 Sim ₃ = 0,6, Sim ₁, Sim ₂, Sim ₄ = 1, а итоговое значение Sim ( Sit_z , Sit_act )при равнозначных элементах сложного объекта равняется 0,85.

Нетрудно заметить, что в частном случае, когда имеется определенность при распознавании состояний, Sim (.) принимает значение 1, если все элементы объекта находятся в одном и том же состоянии в двух ситуациях, и значение 0, когда все состояния элементов объекта в двух ситуациях не совпадают.

Нейросетевая архитектура

Описанные выше модели позволяют разработать нейросетевую архитектуру, которая реализует последовательное преобразование входных параметров сложного объекта в представление ситуации, выполняет сравнение текущей ситуации с ситуациями из БЗ и отбор наиболее близкой из них по формуле (4).

Компонентами нейросетевой архитектуры являются:

• •    классификатор, на вход которого подаются значения наблюдаемых параметров i -го элемента объекта. На выходе классификатора формируется вектор состояний данного элемента, так называемые мягкие метки классов, получаемые с помощью функции активации Softmax [10];

• •    компаратор, на выходе которого формируется показатель сходства двух ситуаций по i -му объекту в пространстве состояний;

• •    выходной нейроэлемент, на выходе которого вычисляется интегрированный показатель сходства двух ситуаций в пространстве состояний.

Для сравнения i -х строк матриц M1 и M2 вводится нейросетевой компаратор, на входы которого поступают векторы состояний для двух ситуаций Sit_Z и Sit_act (рис. 2).

Информационные технологии и оптимизация управления

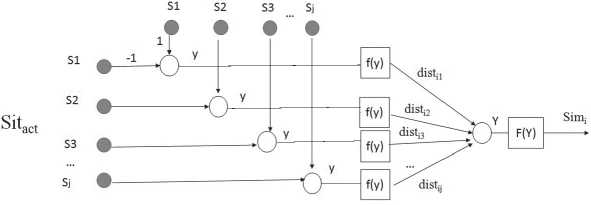
Рис. 2. Нейросетевой компаратор

На рисунке символами y , Y обозначены выходы соответствующих нейронов, которые являются взвешенной суммой входов, при этом веса входов – межнейронные связи – равны 1 или –1 у суммирующих нейронов типа y , и значения весов, равные 1, – на входе решающего нейрона Y .

Нейроны типа y вместе с функцией активации выполняют вычисление по формуле (5), а нейрон типа Y – вычисление Sim_i по формуле (6).

В качестве функций активации выбраны следующие:

f ( y ) = Abs ( y ), где Abs – функция взятия модуля;

F ( y ) = Gauss ( Y ) – функция активации гауссовского типа [2]:

Gauss (Y) = exp[–(Y/b)2c], где b, c – параметры, определяющие ширину и форму колокола функции активации.

Применение функции активации Gauss ( Y ) на выходе нейрона позволяет воспроизвести вычисления по формуле (6), при этом, подбирая параметры b , c можно управлять зависимостью показателя сходства Sim_i от расстояния Dist_i , – уменьшать значение схожести при росте расстояния или увеличивать значение Sim_i при значениях Dist_i до определенного порога. Так, при b = 0,55 и с = 2 получим форму колокола, при которой расстояния в интервале от 0 до 0,4 дают высокие показатели сходства – более 0,7; и, напротив, при увеличении расстояний более 0,5 наблюдается резкое снижение показателя сходства.

Общая нейросетевая архитектура показана на рисунке 3. Здесь на вход подаются наблюдаемые (или прогнозируемые) параметры элементов сложного объекта O_i . Нейросетевой классификатор, в качестве которого для случая табличных данных выступает многослойный перцептрон с функцией активации на выходе Softmax, выдает вектор состояний с вероятностными оценками состояний, которые являются соответствующими строками в матрицах представления ситуаций.

После формирования векторов состояний они сравниваются в компараторах с векторами состояний тех ситуаций, которые находятся в БЗ. Число пар, каскадно объединяющих классификатор и компаратор, определяется числом элементов O_i. На выходе каждой такой пары появляются результаты поэлементного сравнения ситуаций, которые поступают на выходной нейрон. Последний осуществляет взвешенное суммирование по формуле (7), выдавая значение интегрального показателя близости ситуаций Sim ( Sit_z , Sit_act ). Перебором ситуаций в БЗ определяется Sit ^* по критерию (4). При этом сокращение ис-

Представление и отбор ситуаций на сложном технологическом объекте...

ходного множества вариантов обеспечивается предварительным сравнением структуры двух ситуаций, то есть в БЗ отбираются только те ситуации, в которых содержатся только те же элементы и отношения, что и в текущей ситуации [6].

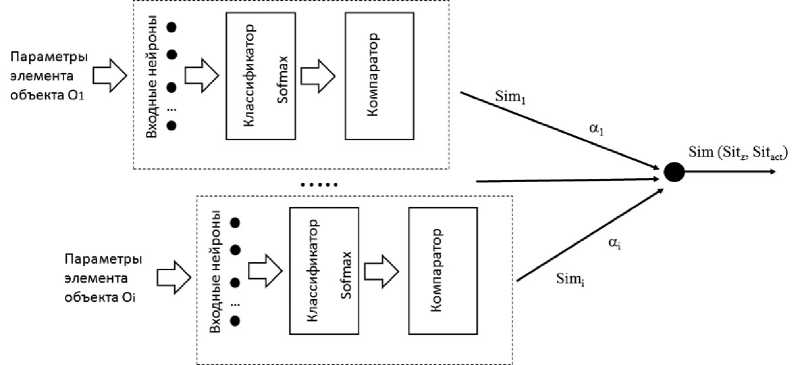
Рис. 3. Нейросетевая архитектура для сравнения и отбора ситуаций на сложном объекте

Заключение

Предложенный подход позволяет декомпозировать сложную задачу распознавания ситуаций в многомерном пространстве на более простые задачи распознавания состояний в пространствах меньшей размерности и последующее сравнение этих состояний в представлении ситуаций из БЗ и ТС.

Известно, что одной из существенных трудностей CBR-метода является выбор метрики для сравнения ситуаций [7]. Это тем более непросто сделать в условиях рассматриваемого сложного технологического объекта, где элементы O_i обладают разной природой, описываются различными наборами разнотипных параметров. Акцент на более простых задачах распознавания состояний позволяет для каждого из элементов создать обучаемые модели нейросетевых классификаторов. При этом сама ситуация на сложном объекте трактуется как комбинация состояний и отношений между элементами сложного объекта, что позволяет при ограниченном и неизменном множестве состояний оперировать значительным числом разных ситуаций. За счет этого можно преодолеть еще одну трудность CBR, которая связана с невозможностью применения предобученных классификаторов для детальной классификации ситуаций по причине появления в ходе работы системы ситуаций нового класса (обладающих новым решением). При этом использование «мягких меток» на выходе классификаторов в виде значений µ _ij обусловливает возможности сокращения объемов данных, необходимых для обучения классификаторов [10].

Предложенные модели и нейросетевая архитектура позволяют реализовать вывод на прецедентах с использованием нейросетей и, таким образом, являются вкладом в решение научной проблемы интеграции машинного обучения и CBR-метода [3, 7–9].

Информационные технологии и оптимизация управления