Представление и применение знаний о кубах-концептах для поддержки адаптивного манипулирования объектами анализа OLAP

Повышение эффективности аналитической обработки больших объемов данных для принятия обоснованных решений требует развития средств адаптивного манипулирования объектами анализа в технологии OLAP (On-line analytical processing) [1–5]. Формирование каталога показателей дает возможность систематизировать объекты анализа, но не позволяет выполнять их совместную аналитическую обработку [2; 6]. Построение онтологии предметной области дает возможность оперировать всеми объектами, включенными в онтологию, но не позволяет оперативно формировать запросы в ходе аналитического эксперимента [7; 8].

В авторских работах [9; 10], построения интегральной аналитической модели предметной области предложен метод концептуального OLAP-моделирования, позволяющий строить интегральную OLAP-модель предметной области в виде решетки многомерных кубов на основе экспертных знаний об объектах анализа и возможности их совместной аналитической обработки [11; 12].

Для реализации оригинального метода разработаны алгоритмы поиска кубов-концептов на основе контекста предметной области и построения концептуальной решетки OLAP-кубов [5; 6]. С целью поддержки адаптивного манипулирования объектами анализа интегральной OLAP-модели актуальной становится задача определения оптимального куба-концепта на множестве всех объектов анализа предметной области.

В работе предлагаются продукционная модель представления знаний о кубах-концептах, упорядоченных отношением Галуа в виде концептуальной решетки кубов, и алгоритм определения оптимального куба-концепта для частной аналитической задачи на множестве всех доступных объектов анализа. Разработанные средства представления и применения знаний о кубах-концептах позволяют осуществлять адаптивное манипулирование объектами анализа OLAP, что значительно повышает эффективность аналитической обработки многомерных данных и способствует обнаружению новых знаний для принятия решений.

Интегральная аналитическая модель предметной области в виде концептуальной решетки OLAP-кубов. Интегральная аналитическая модель предметной области строится путем применения анализа формальных понятий к аналитическим объектам в терминах технологии OLAP. Основу интегральной OLAP-модели составляет множество объектов анализа, которые используются для построения OLAP-кубов: множество показателей F = { f 1 , f 2 , …, f m } и множество измерений D = { d 1 , d 2 , …, d n }. Между элементами множеств F и D определяется отношение сопоставимости R – возможность совместной аналитической обработки показателей и измерений. R c F x D , (f , d j ) e R, если показатель f может быть проанализирован по измерению d j . Тройка ( F , D , R ), в соответствии с теорией анализа формальных понятий [13; 14], представляет собой формальный контекст K . Формальный контекст отражает знания эксперта об объектах анализа предметной области и о возможности их совместной аналитической обработки.

На основе формального контекста K определяется множество концептов – OLAP-кубов (кубов-концептов) по признаку сопоставимости объектов анализа. Для произвольных X c F и Y c D определяется операция «штрих» следующим образом:

X ' = { d e D | V f e X, ( Rd )}; Y ' = { f e F | V d e Y(fRd)}.

Пара ( A , B ), где A c F , B c D такие, что A = B' и B = A' , называется кубом-концептом контекста K . Множество A состоит из показателей одинаковой размерности, которые могут быть проанализированы по всем измерениям из B. ( A , B ) – многомерный куб, полный относительно добавления показателей той же размерности и состава измерений. Множество показателей A представляет объем куба-концепта, а множество измерений B – содержание куба-концепта.

Множество всех кубов-концептов частично упорядочено отношением Галуа: ( A 1 , B 1 ) ≤ ( A 2 , B 2 ), если A 1 c A 2 и B 2 c B 1 [15]. В этом случае, ( A 1 , B 1 ) - подкуб ( A 2 , B 2 ), а ( A 2 , B 2 ) – надкуб ( A 1 , B 1 ). Множество показателей надкуба включает множество показателей подкуба, а в свою очередь, множество измерений подкуба включает множество измерений надкуба. Упорядоченное отношением подкуб-надкуб множество всех кубов-концептов образует концептуальную решетку

OLAP-кубов и представляет собой интегральную аналитическую модель.

Модель представления знаний о концептах – OLAP-кубах

Для поддержки адаптивного манипулирования объектами анализа интегральной OLAP-модели разработана продукционная модель представления знаний о кубах-концептах. Модель основана на свойствах концептуальной решетки, согласно которым: надкуб любого куба-концепта решетки содержит наибольший объем (множество показателей) и наименьшее содержание (множество измерений), а подкуб, наоборот – содержит наибольшее содержание и наименьший объем. То есть, при переходе по ребру решетки от подкуба к надкубу происходит расширение объема и сокращение содержания и аналогично, при переходе по ребру решетки от надкуба к подкубу происходит сокращение объема и расширение содержания. Таким образом, модель знаний, представляющая концептуальную решетку кубов, отражает отношения между кубами-концептами решетки и между объемом и содержанием кубов-концептов. Разработанная модель содержит правила вида:

S:F:N: IF <  ( A cur - A super ) & ( P n X = 0 ) >

• >    THEN <  A cur ^ A sub > ;           (1)

SDN: IF <  ( B cur - B sub ) & ( Q n Y = 0 ) >

• >    THEN < B cur ^ B super > ;           (2)

S:F:N: IF < A _cur - A >  THEN < B _cur ^ B > ; (3) S:D:N: IF < B _cur - B >  THEN < A _cur ^ A >. (4)

Здесь S – уникальное в базе знаний имя правила; F , D – указатель назначения, характеризующий зону действия правила для показателей и измерений соответственно; N – приоритет применения правила, указывающий на преимущественное применение правила при разрешении конфликтов; A cur – начальное множество показателей для процедуры логического вывода; A _sub – объем (множество показателей) подкуба; A _super – объем (множество показателей) надкуба; P – множество показателей, удаляемых из объема надкуба при переходе к подкубу; X – множество показателей, требуемых для аналитической обработки; B cur – начальное множество измерений для процедуры логического вывода; B super – содержание (множество измерений) надкуба; B sub – содержание (множество измерений) подкуба; Q – множество измерений, удаляемых из подкуба при переходе к надкубу; Y – множество измерений, требуемых для аналитической обработки. Символ ^ обозначает переход от одного куба-концепта к другому.

Правила (1) и (2) описывают переход по ребру концептуальной решетки. Правила типа (3) и (4) описывают отношение между множеством показателей и множеством измерений куба-концепта решетки. Правила типа (1) и (2) имеют более высокий приоритет по сравнению с правилами типа (3) и (4). Другими словами, приоритетным является переход от одного куба-концепта решетки к другому. В случае, если ни одно правило перехода не может быть выполнено, осуще- ствляется подстановка множеств показателей или измерений соответственно.

Принципы поддержки адаптивного манипулирования объектами анализа на основе продукционной модели представления знаний. Интегральная аналитическая модель, построенная в виде концептуальной решетки OLAP-кубов, позволяет пользователю проводить аналитические эксперименты на множестве всех доступных объектов анализа предметной области [12]. Свойства концептуальной решетки позволяют определять дополнительные показатели и измерения, которые могут быть проанализированы вместе с выбранными пользователем объектами анализа. Поэтому поддержка адаптивного манипулирования объектами анализа заключается в формировании дополнительных показателей и измерений для оперативной аналитической обработки.

Согласно свойствам концептуальной решетки, множество всех кубов-концептов, удовлетворяющих текущему запросу пользователя, представляет собой подрешетку интегральной модели. Куб-концепт подрешетки, расположенный на самом верхнем уровне содержит максимальный набор дополнительных показателей – максимальный куб-концепт для текущего запроса. В свою очередь, куб-концепт подрешетки, расположенный на самом нижнем уровне содержит максимальный набор дополнительных измерений – минимальный куб-концепт для текущего запроса. Таким образом, определение максимального и минимального кубов-концептов для текущего пользовательского запроса и формирование максимальных наборов дополнительных объектов анализа – основная задача логического вывода.

Процедура определения дополнительных объектов анализа для текущего запроса соответствует прямой цепочке логического вывода и заключается в последовательном сравнении условий правила (антецедента) и выполнении соответствующих действий (консеквента) [16].

Основными параметрами процедуры определения дополнительных объектов анализа являются текущий запрос пользователя, максимальный куб-концепт и минимальный куб-концепт. В начальный момент работы текущий запрос пользователя представляет собой пару (∅, ∅), максимальный куб-концепт – это куб-концепт, расположенный на самом верхнем уровне решетки кубов, минимальный куб-концепт – это куб-концепт, расположенный на самом нижнем уровне решетки кубов. При добавлении показателя в текущий запрос, начальное состояние определяется как множество показателей максимального куба-концепта подрешетки, соответствующей запросу на предыдущем шаге. В качестве входных параметров передаются множество требуемых показателей X и начальное множество показателей Acur. Результат вывода – множество измерений Bcur, определяющее содержание минимального куба-концепта подрешетки, соответствующей запросу на текущем шаге. При добавлении измерения в текущий запрос начальное состояние определяется как множество измерений минимального куба-концепта подрешетки, соответствующей за- просу на предыдущем шаге. В качестве входных параметров передаются множество требуемых измерений Y и начальное множество измерений Bcur. Результат вывода – множество показателей Acur, определяющее объем максимального куба-концепта подрешетки, соответствующей запросу на текущем шаге.

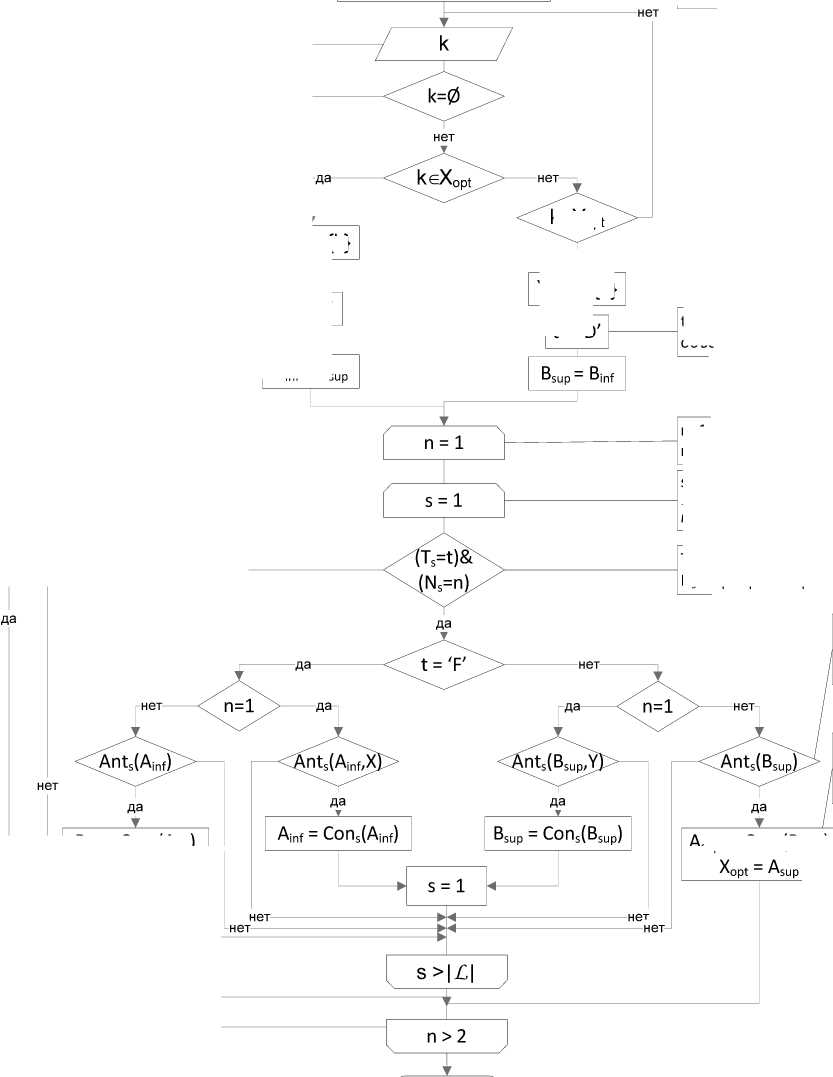
Алгоритм определения оптимального куба-концепта для частной аналитической задачи. Исходя из свойств концептуальной решетки и принципов поддержки адаптивного манипулирования объектами анализа, разработан алгоритм определения оптимального куба-концепта для частной аналитической задачи на множестве всех доступных объектов анализа предметной области. Блок-схема алгоритма представлена на рис. 1.

Алгоритм заключается в последовательном добавлении объектов анализа в пользовательский запрос и определения объема и содержания оптимального куба-концепта на основе применения правил вывода.

Работа алгоритма начинается с определения начального состояния переменных, участвующих в процессе поиска оптимального куба-концепта. Объем и содержание пользовательского запроса определяются как пустые множества. Содержание оптимального куба-концепта X opt равно множеству показателей интегральной модели, объем оптимального куба-концепта Y opt равен множеству измерений интегральной модели. A sup и B sup определяются как содержание и объем максимального куба-концепта решетки, который соответствует точной верхней границе множества кубов-концептов B(K) – sup(B(K)). A inf и B inf определяются как содержание и объем минимального куба-концепта решетки, который соответствует точной нижней границе множества кубов-концептов B(K) – inf( B ( K )).

Затем алгоритм ожидает выбора объекта анализа пользователем. Если объект анализа не был выбран, то алгоритм прекращает свою работу. После выбора объекта анализа определяется его тип, путем проверки вхождения k в множество X _opt. Если выбранный объект принадлежит содержанию оптимального куба-концепта, то k добавляется к содержанию пользовательского запроса X , тип объекта анализа t для выбора правил определяется как ‘ F ’ и значение A _inf устанавливается равным A sup . Если выбранный объект принадлежит объему оптимального куба-концепта, то k добавляется к объему пользовательского запроса Y , тип объекта анализа t для выбора правил определяется как ‘ D ’ и значение B sup устанавливается равным B _inf . Если выбранный пользователем объект анализа не принадлежит оптимальному кубу-концепту, то алгоритм возвращается на этап выбора нового объекта анализа.

Для выбора правил в соответствии с их приоритетом, определяется параметр n , принимающий значения 1 и 2. Затем в цикле по s , где s изменяется от 1 до мощности множества правил |L|, описывающих интегральную модель, происходит сначала выбор правила в соответствии с установленными значениями t и n , а затем проверка условий применимости правила и его выполнение.

Г начало

(X, Y) = (0, 0)

^(Х, Y) - запрос пользователя

XOpt = F

Xopt - содержание оптимального куба-концепта

Yopt = D

(A$up, Bsup) = sup((B^

Yadd - объем оптимального куба концепта sup(6(%i) - максимальный куб-концепт решетки Ф^

inf(Ф^

(Ajnf, Binf) - inf(®(^))

к - объект анализа, добавляемый пользователем в запрос

KETopt t ='D да

Cons-консеквент правилаs

Ants-антецедент правилаs

Ts - назначение (тип) правила s

Ns - приоритет применения правила s

( конец )

Рис. 1. Блок-схема алгоритма определения оптимального куба-концепта

Bjnf - Cons(Ajnf)

YOpt — Bjnf

X=Xu{k}

t = T

Ajnf ~ A<

Y=Yu{k}

t - тип добавляемого в запрос объекта нализа

n=l, 2 - приоритет применения правила s=l,|£|- идентификатор правила L-множество правил интегральной модели

‘sup ~ Cons(Bsup )

f1 f2 f3 f4

Число публикаций

Число материалов конф-ий

Число учебных пособий

Число объектов интел. соб-ти

d1

d2

d3

d4

d5

d6

d7

d8

d9

d10

f5

Число конференций

x

x

x

x

x x x

x

x

x

x

x

x

x

x

x

x

x x x

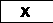
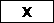
x

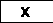
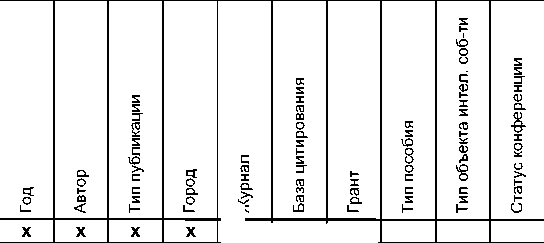
Рис. 2. Фрагмент формального контекста научной деятельности организации

При t =’D’ и n = 1 для проверки антецедента правила используется множество B sup и объем пользовательского запроса Y . В случае выполнения условий антецедента значение B _sup меняется в соответствии с консеквентом правила и проверка правил начинается с начала цикла.

При t =’D’ и n = 2 для проверки антецедента правила используется только множество B sup . В случае выполнения условий антецедента значение A sup меняется в соответствии с консеквентом правила, содержание оптимального куба X opt становится равным A sup , заканчивается проверка правил и алгоритм переходит на этап выбора нового объекта анализа.

Таким образом, алгоритм обеспечивает поддержку построения пользовательского запроса для частной аналитической задачи в соответствии с интегральной OLAP-моделью и формирует оптимальный куб-концепт ( X opt , Y opt ) на каждом шаге построения пользовательского запроса. Объем найденного оптимального куба-концепта соответствует нижнему кубу-концепту подрешетки кубов, удовлетворяющих пользовательскому запросу, и содержит максимальное количество измерений для совместной аналитической обработки с текущим запросом пользователя. Содержание найденного оптимального куба-концепта соответствует верхнему кубу-концепту подрешетки кубов, удовлетворяющих пользовательскому запросу, и содержит максимальное количество показателей для совместной аналитической обработки с текущим запросом пользователя.

Адаптивное манипулирование объектами анализа на основе интегральной OLAP-модели научной деятельности организации. Рассмотрим реализацию принципов адаптивного манипулирования объектами анализа и работу алгоритма поиска оптимального куба-концепта для интегральной OLAP-модели научной деятельности организации.

На рис. 2 представлен фрагмент формального контекста научной деятельности организации, строки которого соответствуют показателям, а столбцы – измерениям. Используя сокращенные обозначения, получим соответственно: F = {f1, f 2, f 3, f 4, f 5} и D = {d1, d2, d3, d4, d5, d6, d7, d8, d9, d10}. Отношение R записывается следующим образом: R = {(f1, d1), (f1, d2), (f1, d3), (f1, d4), …, (f5, d10)}.

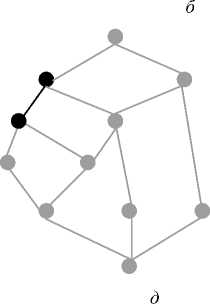
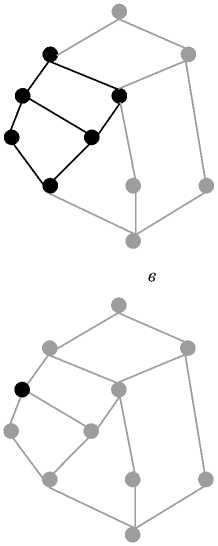
На рис. 3 приведена концептуальная решетка OLAP-кубов, построенная в рамках рассматриваемого формального контекста и представляющая интегральную аналитическую модель научной деятельности. На рис. 4 проиллюстрировано соответствие подрешетки запросу пользователя на каждом шаге логического вывода.

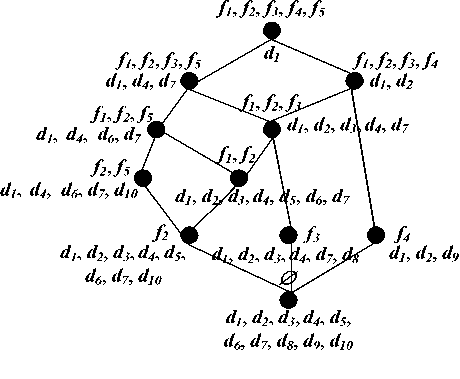
Рис. 3. Концептуальная решетка OLAP-кубов научной деятельности организации

Разработанные средства представления и применения знаний о кубах-концептах позволяют осуществлять адаптивное манипулирование объектами анализа предметной области.

Возможность выявления аналитических зависимостей между объектами анализа позволяет значительно повысить эффективность аналитической обработки данных и способствует обнаружению новых знаний для принятия управленческих решений.

г

е

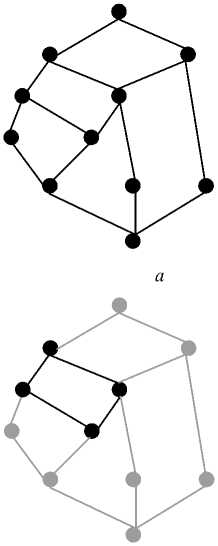
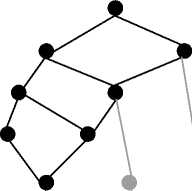
Рис. 4. Соответствие подрешетки концептуальной OLAP-модели запросам пользователя: a) - ( 0 , 0 ); b) - (f2, 0 ); c) - (f2, d7); d)- ({fl, f2}, d7); e) - ({fl, f2, f5}, d7); f) - ({fl, f2, f5}, {d6, d7})