Представление изображений плоских и пространственных объектов набором эллипсоидов

Всякое преобразование в обработке изображений направлено на выявление тех или иных свойств изображений. Преобразование Фурье, например, выявляет частотные характеристики изображений, представление изображения в виде векторного поля позволяет проанализировать дифференциальные свойства первого порядка. В работе рассмотрен подход к выявлению и анализу геометрических характеристик двух- и трехмерных изображений на основе представления последних набором геометрических примитивов – эллипсоидов.

Подход к построению представлений двумерных форм в виде набора аппроксимирующих геометрических примитивов предложен в работе [4]. Развитие такого подхода в сочетании с методами рекурсивной декомпозиции образов на сегменты предложено в работах [3], посвященных разработке древовидных инвариантных представлений образов геометрическими примитивами заданной формы. В отличие от перечисленных работ вводится арифметика геометрических примитивов, рассматриваются методы фильтрации и интерполяции изображений на основе анализа их геометрических характеристик.

Рассматриваемые представления изображений являются сжатыми описаниями образов с требуемой точностью, которая определяется заданной допустимой погрешностью аппроксимации сегментов примитивами, что делает такой подход приемлемым для обработки изображений со структурной избыточностью [6].

В работе рассмотрены основные характеристики эллипсоидов в n -мерном аффинном пространстве, определена операция сложения эллипсоидов и их взвешенная сумма. За рамками работы остались методы представления изображений набором эллипсоидов, а также интерпретация и анализ мнимых эллипсоидов.

Характеристики эллипсоидов в n -мерном аффинном пространстве

E ( Q ) = { p е A : Q ( p ) = 0 }                    (1)

где Q ( x ) = x^TBx + b T x + c - аффинно-квадратичная функция, B – положительно, либо отрицательно определенная матрица квадратичной формы, b – вектор, c е R , определяет один из следующих видов геометрических объектов [1]:

• (I)    эллипсоид

В этом случае - c ₀ ^{- 1} B - положительно определенная матрица, где c ₀ = c - 4 b T B b . К данному типу отнесем также вырожденный эллипсоид (множество, состоящее из одной точки), получаемый в случае, когда B – положительно определенная матрица и c ₀ = 0.

• (II)    мнимый эллипсоид

В этом случае - c ₀ ^{- 1} B - отрицательно определенная матрица. К данному типу отнесем также вырожденный эллипсоид, получаемый в случае, когда B - отрицательно определенная матрица и c ₀ = 0.

• (III)    множество точек аффинного пространства A , которое может быть получено из (1) в случае, когда все коэффициенты аффинноквадратичной функции равны нулю E ( 0 ) .

• (IV)    пустое множество i , которое получается из (1) при B = 0 , b = 0 , c * 0 .

Далее будем рассматривать множество Eⁿ , элементами которого являются квадрики указанного вида в n -мерном аффинном пространстве. Определим операцию сложения элементов множества Eⁿ . Рассмотрим множество эллипсоидов { E ( Q^m ) }   с E n и запишем формальную сумму вида

M

E ( Q i ) = E | £ Q = 0 |                     (2)

• \ m =1           /

которая в нашем случае имеет смысл только, если E ( Q _z) с E n , что определяется видом функций Q^m . Ясно, что рассмотренное множество Eⁿ является незамкнутым относительно рассматриваемой операции сложения (2).

В случае, когда выражение (2) имеет смысл, будем называть его суммой элементов пространства Eⁿ . Следует отметить, что элемент III типа играет роль нулевого элемента относительно операции сложения (2). Рассмотренная операция сложения, в случае, когда выражение (2) имеет смысл, является коммутативной и ассоциативной.

Утверждение 1. Пусть имеется пара эллипсоидов Iтипа (II типа) E(Qi), Qi =(x-r)T B (x-г) + c1, i = 1,2 . Результатом сложения пары эллипсоидов является: эллипсоид I типа (соответственно , II типа), если его центр g , определяемый выражением gT =(rT B1 + r2TB2)(B1 + B2) 1, принадлежит множест- ву решений системы

Q i <  0

Q 2 <  0

(то есть лежит в пересе-

чении внутренностей и граничных точек слагаемых эллипсоидов). Эллипсоид II типа (соответственно, I типа), если его центр g принадлежит множеству решений f Q1 > 0

системы <       . Примеры суммы пар и троек эллип-

[ Q 2 >  0

соидов в двумерном случае представлены на рис . 1 (результирующий эллипсоид показан темным цветом).

Очевидно, что само по себе умножение эллипсоида на произвольное неотрицательное число a E ( Q ) = E ( a Q ) , а >  0 не имеет смысла, однако можно записать вполне осмысленное выражение

MM

E ( Q j = Z a m E ( Q m ) = E I ^ a m Q m l (3) m =1 \ m =1 7

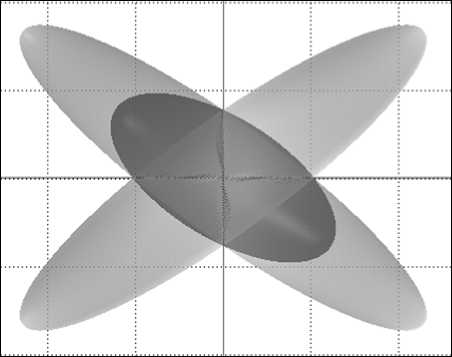
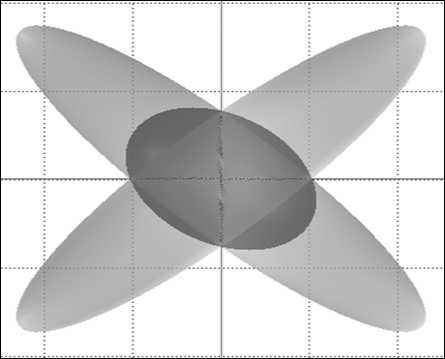
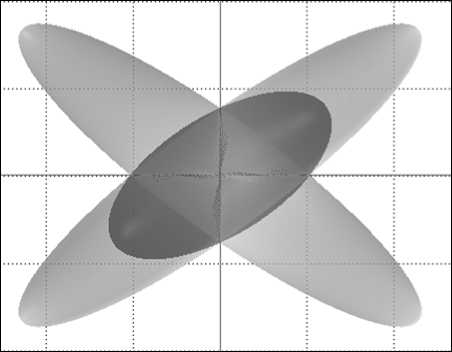
для Va k >  0, k = 1, M , которое будем называть взвешенной суммой эллипсоидов. Взвешенная сумма аффинно-квадратичных функций имеет очевидный смысл. Примеры взвешенной суммы пары эллипсоидов в двумерном случае приведены на рис. 2. Далее суммой эллипсоидов будем называть именно взвешенную сумму.

Утверждение 2. Пусть имеется пара эллипсоидов I типа (II типа) E ( Q ₁ ) , E ( Q ₂ ) , множество Q точек пересечения внутренностей которых не пусто. Тогда результатом сложения является эллипсоид E ( Q x ) такой, что множество решений неравенства Q _z <  0 целиком содержит множество Q . То есть внутренность E ( Q _x ) в совокупности с граничными точками содержит множество Q .

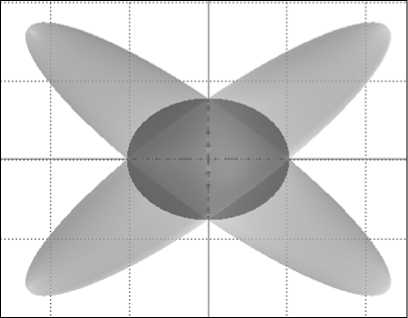
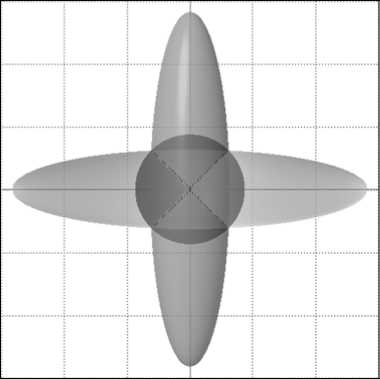
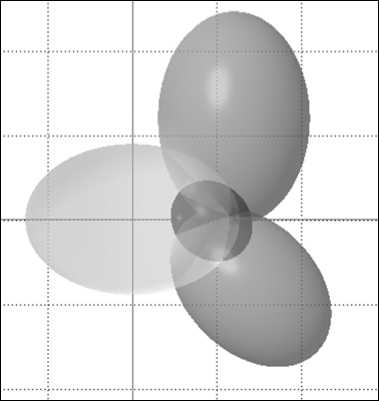
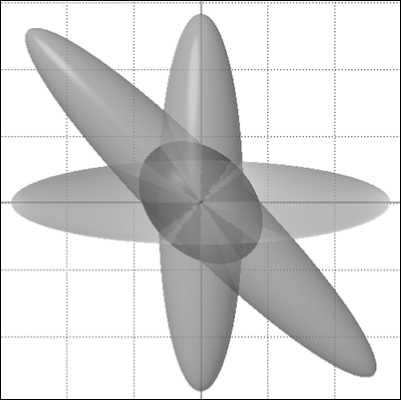
Рис. 1. Примеры сложения эллипсоидов

б)

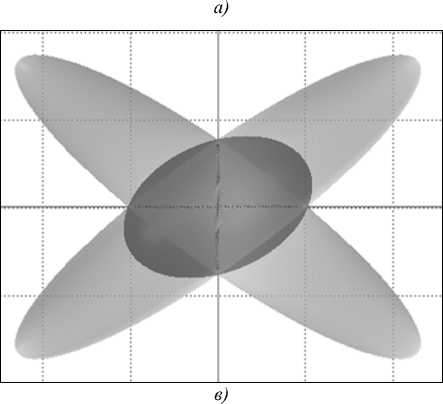
Рис. 2. Примеры взвешенной суммы эллипсоидов с отношением весов: а) 6:1; б) 2:1; в) 1:2; г) 1:6

г)

Утверждение 3. Пусть имеется пара эллипсоидов I типа (II типа) E ( Q 1 ) , E ( Q 2 ) и Q - множество точек объединения их внутренностей и граничных точек. Тогда результатом сложения является эллипсоид E ( Q _z) такой, что множество решений неравенства Q _z <  0 целиком содержится во множество Q .

Представление изображений в виде набора эллипсоидов

Пусть имеется функция f ( x ) , x = ( x 1 ,..., x n ) е D , где D c R n - область определения функции. Положим, что в каждой точке x е D изображения каким-либо способом определен эллипсоид I типа с центром в данной точке:

E (Q (x )) =

{у е Rn : yTA (x) у - 2bT (x) x + c (x) = 0} где A (x) - положительно определенная симметричная матрица, bT = xTA (x), c (x) = xTAx -1. Таким образом, функция f представляется набором эллипсоидов (4). В случае, когда имеется дискрет- ное изображение в выражении (4) изменится лишь то, что x будет принимать дискретные значения.

Эффективный подход к построению представлений двумерных форм на основе их аппроксимации геометрическими примитивами рассмотрен в работах Voss, Suesse [4]. Различные методы древовидных инвариантных представлений образов геометрическими примитивами заданной (в том числе и эллиптической) формы предложены в работах Ланге М.М., Ганебных С.Н. [3].

Рассмотренное представление изображений является сжатым описанием образов с требуемой точностью, которая определяется заданной допустимой погрешностью аппроксимации сегментов примитивами. Достоинством такого представления является то, что при обработке и анализе изображений, представленных в виде (4), одновременно учитывается как форма геометрического примитива, так и его пространственное положение.

Фильтрация изображений, представленных набором эллипсоидов

Представление изображений в виде набора эллипсоидов (4) позволяет производить фильтрацию по различным геометрическим характеристикам. В качестве примеров, в работе рассмотрены два вида:

фильтрация множества эллипсоидов по направлениям (аналогично фильтрации поля направлений [5]) и фильтрация по линейному эксцентриситету – в двумерном случае (для выделения протяженных участков изображений).

Для фильтрации множества эллипсоидов по направлению необходимо задать некоторое направление I и для каждого эллипсоида определить главные направления. Приведем квадратичные функции Q ( x ) к главным осям разложением матриц A ( x ) по собственным векторам [2]: