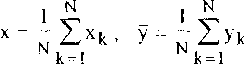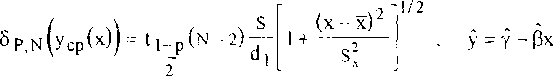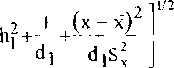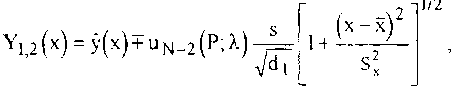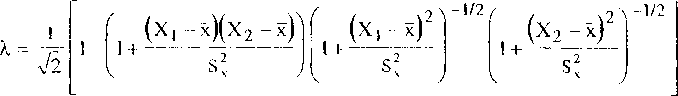Представление экспериментальных функций в определяющих соотношениях термовязкопластичности на основе анализа инвариантных свойств

Термомеханические процессы для широкого класса реальных сред и внешних воздействий описываются системой уравнений, замкнутой тензорно линейными определяющими соотношениями с экспериментально определяемыми скалярными функциями, связывающими инварианты тензоров напряжений, скоростей деформаций и температуру [ 1 - 3 ].

В предлагаемой работе задача восстановления функций по данным опыта рассматривается с позиций выявления возможностей и направлений совершенствования базового эксперимента, упрощения и повышения точности решений математических задач за счет использования инвариантности физических законов Изучается возможность адекватного представления опытных данных функциями [ 4 ], связанными с инвариантными свойствами замкнутой системы уравнений. Предложенный на основе специфики этих функций способ обработки экспериментальных данных включает определение диапазона адекватного описания и алгоритмы вычислений свободных параметров без конкретизации аппроксимирующей функции. Ее конкретизация может быть использована в дальнейшем как для уточнения аппроксимации, так и для упрощения математических задач. Разработаны два дополняющих друг друга варианта реализации способа, основанные на разных свойствах функций. Вариант 1 [ 5 ] на основе специфики геометрического образа дает области допустимой вариации свободных параметров, определяемые точностью исходных экспериментальных данных. Вариант 2, излагаемый ниже, включающий статистический анализ, дает значения параметров и оценки точности в соответствии с выбранным критерием адекватности.

Класс скалярных функций для определяющих соотношений

Неизотермические без массовых сил течения однородной изотропной несжимаемой среды с вязкими и пластическими свойствами описываются [ I - 3 J замкнутой системой уравнений pv = -Vp + VS,     t = v (f(T)VT)+ko.,vj , Vv = 0.

S - aj /vj V , V - defv , оj = ф(vJ ,t), f > 0 , Ф > 0 .

где S и V - девиаторы напряжений и скоростей деформаций, р - давление, Oj=u/V3, vj^v_u^3/2 ; g_u , v_u - интенсивности напряжений и скоростей деформаций. Уравнение притока тепла преобразовано за счет выбора Т и f в уравнение с приведенным коэффициентом теплопроводности f(T) .

Класс {ф} функций Ф( , обеспечивающих расширение возможностей упрощений системы и ее квазистатического и бездиссипативного приближений [ 4 ], приведен в таблице 1.

		Таблица 1
Ф1	f	Ф,
Фо - T(T)v?	f = f (Т)
Ф1 = T'^vjT Р)	f - та	Ф3 - vj’^Tv™)
Ф2 = eyTT(vje"(3T)	f = e“T	Ф2 " vj Ч'(т + mln vj )
Ф3         -pinj)	f = Tra	Ф3 enVj ^(Te™'1)
Ф4 = e^vj - рт)	c f = e	Ф4 = env J Ч^Т + mvj)
Ф5 =ylnT + 4,(vJT"|i)	f = Tx	Ф5 = nlnvj +4,(Tvjn)
Ф6 = уТ +^vje ^Tj	f e'	Фб = nln vj + ^T +mlnvj)
Ф7 - ylnT + ^vj -plnl)	f = const	Ф7 = nvj + 4,(le,Wj)
Ф^уТ + ^-рт)	f = const	Фх = nvj + Ч*(т + mv j)

В таблице 1 функции f и Ф эквивалентны функциям f'

и Ф'

f' = f(bT + bo) , Ф' - a ^(a^j + а0 ,ЬТ + Ьо)+а()о ,где b0 , b , ак произвольные константы, к зависит от выбранного приближения системы и геометрии течения. Функция T(z) - произвольная функция одного аргумента, ос , Р , у (или а , m , п ) - экспериментально определяемые константы, независимые или линейно связанные в зависимости от приближения системы.

Геометрические свойства

В евклидовом пространстве Т , vj , Oj с репером е, , e, ej — 5ц каждая из функций Фк е{Ф} задает двухпараметрическое семейство поверхностей лк с общими свойствами.

Утверждение 1. Каждая из поверхностей лк может быть непрерывным деформированием без искажения координатной сети на ней преобразована в любую другую поверхность л; .

В качестве доказательства приводим (таблица 2) явный вид взаимно однозначных преобразований 9 = 9(Т) , w = w(vj) , s=s(oj) , переводящих все поверхности лк в поверхность к, к : s= у9 + y(w - р9) , s= nw +

Таблица 2

ф,	W	9	s
ф()	In Vj	T	ln	In^z)
Ф1	Invj	InT	InCTj	lniP(exp z)
Ф7	Invj	T	Inoj	lnT(exp z)
ф3	vj	InT	InCTj	InT(z)
ф4	VJ	T	Inoj	In^z)
ф5	In V|	InT	°J	TTexpz)
Фб	Invj	T	°J	T'(expz)
ф?	VJ	InT	°J	T(z)
ф8 _	VJ _____	T    .....	____ ° J ____	__ ^(z) ...... ......

Поверхность тг - цилиндрическая поверхность, образованная параллельным переносом произвольной кривой в направлении

Н = е|+Ре9 + уёд , R- е^ ть 0 ; R = ШSj + i^TnS^ ,       (2)

R ■ 62 * 0 ; mP = -1, пр = у .

Замечание. В пространстве Т , vj , oj поверхность oj = $(vj ,т), за исключением частных случаев, как Ф8 , не есть цилиндрическая.

Зависимость (1) s=s(w, 9,р,у) - общее решение уравнения s,S +P,w = Y

Свойства л_к обусловили возможность анализа соответствия данным опыта одновременно всех функций Ф_к е{Ф} и получения алгоритмов вычисления параметров у, Р , Ж , П независимо от T(Z) .

Свойства опытных данных

Исходная информация об анализируемой реальной зависимости aj T’(vj,T может быть задана в виде а) эмпирической функции, в) серии кривых oj = Oj(vj)

Т = const или CTj = CTj(T) , vj --const , с) серии кривых с полосой разброса, d)

множеством точек, е) множеством точек с допусками. Пусть, например,

)Vj z или joj ,vj ? i = l,n ;j-l,m              (4)

результаты измерений Oj (или vj ) при независимо варьируемых v) , Tj ;

vj 1 < vj < Vj+1 , TJ-1 < T* < T,+1 (аналогично при oj , Tj ), прошедшие предварительную статистическую обработку: исключение систематической ошибки, проверку на приемлемость по критерию оценки резко отличающихся значений, проверку однородности выборок, оценку точности индивидуальных показателей.

Опубликованные данные показывают, что для многих материалов oj lj

У"1 ij

CT j    > CT J

/ 1 + li I                 У UV i + 1

Изучение возможности адекватного представления данных опыта функциями

Фк е{Ф} базируется на свойствах (1) - (3), (5). В [ 5 ] эта задача решаегся геометрически сведением к поиску' параметрического вектора (2). При решении задачи с применением статистических методов [ 6 ] будут также использоваться свойства (1) - (3), (5) и специфика данных инженерного эксперимента.

В статистической практике исследование зависимостей по результатам наблюдений сводится к поиску наилучшей, в смысле выбранного критерия, аппроксимирующей функции из заранее выбранного исследователем класса (линейные, полиномы, и т.п.) обычно за счет подбора по данным опыта значений параметров. При этом возникают вопросы: 1) влияние точности измерений, 2) степень точности восстановления зависимости по данным ограниченного числа наблюдений, 3) математическая структура модели, 4) выбор критерия качества аппроксимации и в соответствии с ним наилучшая ее реализация, 5) алгоритм обработки данных, 6) оценки точности. Для проверки различных гипотез о структуре модели разработаны статистические критерии, основанные на поиске компромисса между сложностью модели и точностью, на поиске модели, наиболее устойчивой к варьированию состава выборочных данных; на сравнении критериев адекватности и исследовании статистических свойств оценок. Для определения же структуры модели теоретическая основа, дающая строгие стандартные методы, отсутствует.

Для выяснения возможности и точности описания данных (4) функциями Ф1 , выбирая для поиска наилучшей аппроксимации класс {Ф} (1), используя его свойства (2), (3), (5), можно сохранить произвол в o(z) .

По данным (4) и таблице 2 введем для каждой точки V) , Т^J величины х? = (s^{i + ,J} - s^fw’ "' - w¹?¹ , х« = (_sy - s^Vw¹ - w¹-’) ' ,

‘J _ („У+¹ ijVnj+l a j) ¹ ‘J - L‘j _ Jj-lVqj - qb¹^ ¹

У I — I о         S It v         <7 I , у 2 — I Ь S И J <7 J ij I У У

X J £pf ,X2

y'J

[ti У1

У] >У2]

для оценки на плоскости хоу анализируемой зависимости у - у - рх и / ii Й

Перенумеруем точки ~ ^+хгу > У ~:ДУ1⁺У2) для определенности в порядке возрастания х^у , включая точки совпадениями рассмотрим совокупность {^xkAk} - k = !,N; N mn где, возможно, 1; i = 1,к - количество точек у^ при i-м фиксированном значении аргумента х-* (или в i-м интервале группирования по X со средней точкой X; ).

Для оценки степени тесноты связи по выборочному значению коэффициента корреляции Г , I г | < 1 , значение которого । г | = 1 соответствует наличию анализируемой функциональной связи, имеем

1   ( 1 N

’      ’ >>кУк ху

SxSy^k^

Ч >(хк х) ,  5у--^(Ук-у)

к = 1                    Nk = l

Отсутствие корреляционной связи в (6) можно проверить по критерию

|r|>-2          

где to ostN - 2) - 5% -я точка распределения Стьюдента с N-2 степенями свободы. При выполнении (8) связь отсутствует.

Доверительный интервал, в котором с доверительной вероятностью Р = 1 - а находится истинное значение Г , вычисляется по доверительному интервалу | / t z 2 ] величины М Z в виде

Z = —In-—/ arcthr ; Z12 = arcthr + на/2(м - з) 1/2---г(м-1) V где u(t/2 - 100—% -я точка стандартного (0,1) нормального распределения thZj < г < thZ2

Свойства зависимости (1) позволяют воспользоваться критерием W2

1 k

(N-k)(p2-F2)         N^11^1

У1=Г^Уц

(к-2)1-р2                    -\2

По заданному достаточно малому значению а находится 100а% -я точка

V(Z распределения р(к - 2, N - к)

При W2 < V2

представление (1) в

рассматриваемом диапазоне w , 9 не противоречит экспериментальным данным, при W2 > v(2 представление (1) неприемлемо.

Значения параметров

Наилучшая аппроксимация в двухпараметрическом семействе s - s(w, 9; Р, у найдется как решение оптимизационной задачи s = argminAN(s),

se{s},

где A_n(s) - критерий адекватности, функционал, характеризующий качество аппроксимации функцией s из класса {s} Свойства (1), (3) - (6) позволяют свести решение экстремальной задачи к определению по (6) наилучших значений парамегров Р , Y . Выбирая за критерий адекватности МНК-функционал, дающий, как известно, состоятельные, несмещенные, эффективные оценки, получим для р , у систему двух линейных алгебраических уравнений.

Условие минимизации А^(р,у)-э min :

1 N

AN (Рл) =     Z hГ2 (xkXvk - Y + pxk)2 ,

(Ю)

N k-l дает оценки P , у параметров P , у как решение системы aio(xb.-,xN)p + an(xl,...,xN)Y + bI(xI,...,xN;y1,...,yN)=O,(11)

NNN аю = Еь12(хкМи, ап = -ЕьГ2(хкН, ь, = Zh^xjxU, 1 = 0,1, к-1                       к=1к = 1

Р = (а01Ь] - Ьца^Д 1 ; у = (ащЬра00Ь])д Д = аоОап - а10а0|.

Условие А^ (т, п) -> min:

m,n

1 N3

AN(m,n)- -£h;2^^^(12)

k-l приводит к оценкам m = (aHb0-ащЬ^Д"1 , n = (a10b0 -а^Ь^Д-1,(13)

где Л|о , а15 , bj , А вычисляются по (11) при формальной замене хоу ; h^x) , h2(y) - функции, задающие зависимости условной дисперсии результирующего показателя от аргумента.

При нормальной минимизации Ам(Р, '/) ^ m*n

параметры Р , у имеют вид

y=y°+px , Y° =-T-Zhlk2yk ,    P---- dlkl

2r

Sy = VS()+4f2

So

/S,SV

где коэффициент корреляции и выборочные дисперсии если hj = const , в общем случае по формулам

вычисляются ио (7),

S

N

/ N                                       '.

d-5>^xkyk-x<2>y*2»j

V°2 k=l                  )

1/2

S = sV^V^S;^

’ h2k

Z^k-

y^Z^yk

> dj =

п

£1^; 1 = 1,2, к=1

- d!. Z ’ь/Ьк '

1 k=I

S'1

N

k=l

Степень точности удовлетворения условий mP = -l и пр =;/ определяется ■значениями р , у , m , п , вычисленными по (11), (13), (14), и степень близости к нулю острого угла б , отсчитываемого от у = у - рх , к х = п + ту , в положительном направлении 5 > О tg5 ® (1 - r)2SxSy /r(s2 +S2)

дадут дополнительную информацию о соответствии (1) и (4)

Оценки точности

Анализ точности восстановления истинных зависимостей аппроксимаций по выборочным данным состоит в определении предельных величин погрешностей, за которые с заданной доверительной вероятностью не выходит ошибка при замене истинного значения его статической оценкой. Их получение опирается на результаты статистического исследования выборочного распределения относительно истинных значений оцениваемых величин; для отношения отклонения выборочного значения от истинного к характеристикам дисперсии принимается распределение Стьюдента. В применении к нашему случаю для оценки точности соответствия (Г) и (4) существенны доверительные интервалы, в которых при заданных N, Р с вероятностью, не меньшей, чем Р , будут находиться значения изучаемых характеристик и доверительная область для истинной зависимости

Доверительные интервалы для параметров [pj,^] , [уьУг]:

Р1.2 Р + 5Р N(p) , Yi^ - Y°+5р N(y°) ;     |р-р| < 6P N(p) ;

I 0 -ОНе ( ()\ |у -у |<5р N^y ),

к

8р.м(Р)^ Д-Р^-2)8 ZJihii2

л-1/2

5p,n(y

к

*1-1/2

, S2

k 1,

2                      J п             -                      -О

Доверительный интервал У1-У2 фиксированном значении аргумента

YL2 - у(^х) ⁺ 5р^(уср(^х)/ > |у

i = 1j=1

У1Г у+Й?)"

для условного среднего при

Доверительный интервал [УьУ2] Д-™ индивидуальных значений при фиксированном значении аргумента

Yl,2(x) ^y(x)+5P N(y(x));    | у(х) - у(х) | < 5Р N (у(х)),

г s P.N(у(х)) t I P (N 2)s

Доверительная область Х]<х<х2 , У1(х) < у < у2(х) для истинной зависимости, в которой она находится с доверительной вероятностью Р , строится после вычисления величины X и определению по ней и заданной Р затабулированной величины и(Р;Х) в виде [7]

Примеры расчета

Изложенным способом проведена обработка экспериментальных данных [ 8 ] для ряда металлов и сплавов в температурно-скоростном диапазоне горячей обработки давлением. Примеры результатов расчета по данным ^ ,Tj,ctjJ^ , N - 20 для Т1:900,1000,1100,1200° С ; v2:10 '* т Ю2 1 / с приведены в таблице 3. Расчеты показывают, что для вероятности ошибки I — Р = 0,01 и степени свободы N —2 — 18 (табличные значения г*-0,561 , 1* - 1,734 ) сдвиговое сопротивление стали 4X13 в данном температурно-скоростном диапазоне может быть представлено любой из функций Ф[ , i = 1,4 , а стали 12ХНЗА - не любой. Сдвиговое сопротивление сплава

ХН75МБТЮ может быть представлено любой из функций Ф^ , i - 1,4

Таблица3

Марка сплава	Параметры и критерии	Значение параметров и критериев
		Ф,	ф2	Фз	Ф4
Сталь	Р	37,92	7,56	0,02	14,02
4X13		-0,15	0,22	0,00	-0,61
8 = 20%	Y	0,88	0,63	0,81	0,73
	Г t	-10,1	-3,51	-7,69	-5,78
Сталь	р	2,34	0,00	0,00	0,23
12ХНЗА		-6,88	0,14	0,14	-0,56
е = 40%		0,14	0,13	0,07	0,06
	г 1	-0,68	-0,66	-0,35	-0,33
Сплав	р	38,13	7,98	0,02	23,96
ХН75МБТ		-0,64	0,25	0,00	-0,51
. Ю		0,92	0,63	0,86	0,76
е 40%	Г t	-12,53	-4,43	-9,10	-6,41