Преимущества использования электронных таблиц при выполнении студентами письменных работ

1.    Введение.

Недооценёнными студентами средствами решения самых разнообразных экономических задач на уровне общего вузовского образования являются популярные модели процессоров электронных таблиц (сокращённо называемые табличными процессорами или электронными таблицами – ЭТ). В середине 1990-х годов ими в России недолгое время являлись ЭТ Quattro pro [5], [15]. Затем, до настоящего времени включительно, наиболее распространёнными компьютерными программами этого класса в РФ являются различные версии MS EXCEL [1], [2], [4], [8], [10], [11], [13], [16], [17].

Процессоры электронных таблиц (даже без учёта возможности программирования в их среде [2], [15]) по сравнению с: 1) специализированными профессиональными пакетами прикладных программ (ППП), а также 2) компьютерными деловыми играми, обладают следующими основными преимуществами [4], [11]: а) универсальностью, б) «прозрачностью» вычислений.

Большая универсальность ЭТ по сравнению со специализированными ППП (в частности, одного уровня по интерфейсу, например, MS PROJECT и MS EXCEL) помогает пользователю улучшать (оптимизировать) подготовленные экономико-управленческие решения (см. табл. 1).

Таблица 1. Возможности MS Project и EXCEL по обеспечению управления проектами

№	Действия по управлению проектами	Возможности оптимизатора «Поиск решения» EXCEL	MS PROJECT
1.	Планирование задач (работ)	[8], глава 7-я (с. 226 – 229), [11], глава 1-я (с. 118 – 124).	[1], глава 2-я (с. 17 – 48).
2.	Планирование трудовых ресурсов	[1], глава 3-я (с. 51 – 67) {решение задачи о назначениях с целью минимизации трудозатрат}.	[1], глава 4-я (с. 77 – 81) {приём ответа из EXCEL}.
3.	Планирование затрат	[1], глава 5-я (с. 86 – 90) {решение задачи о назначениях с целью минимизации денежных затрат}	[1], глава 6-я (с. 91 – 96) {приём ответа из EXCEL}.
4.	Сокращение продолжительности проекта { CPM/Cost }	[8], глава 7-я (с. 231 – 243)	[8], глава 7-я (с. 244 – 257).

Таблица 2. Примеры возможностей применения графиков функций EXCEL для выполнения письменных работ студентов: менеджеров и экономистов.

Название предметной области	Графики линейных функций на одной диаграмме	Графики нелинейных функций на одной диаграмме	Графики функций от двух переменных (для каждой функции одно значение пары координат аргументов) на одной диаграмме
Экономическая теория	«Паутинообразная модель» сходимо-сти к рыночному равновесию [4].
Стратегический и оператив-ный менеджмент	Однопродуктовый анализ продаж с одной точкой безубыточности [4].	Однопродуктовый анализ продаж с двумя точками безубыточности [4].	Матричная диаграмма Бостон-ской консультативной группы (БКГ) [4], [14].
Маркетинг			Матричная диаграмма «Свойства продуктов – сегменты рынка».
Логистика	Графическое решение задачи «Делать или закупать?» [4].	Графическое решение задачи «Где (в каком регионе) закупать?» [4].	Графическая поддержка вычисления методом центра тяжести грузопотоков места размещения оптового склада [4].
Инвестиционный анализ		Графики зависимости NPV(R) [4].

Анализ табл. 1 показывает, что оптимальные решения, полученные в EXCEL, затем переносятся в PROJECT, где встроенный оптимизатор отсутствует.

Второе преимущество («прозрачность» расчётов) есть следствие отсутствия необходимости сохранения «ноу-хау» авторов алгоритмов моделирования, применённых в компьютерных программах коммерческого (как профессионального, так и учебного) назначения.

В оригинальной статье [6] аналогичными преимуществами наделён текстовый процессор MS WORD. Если признавать эти преимущества за текстовыми процессорами (по крайней мер, – за MS WORD), то, тем более, логично, признать их за процессорами электронных таблиц (в том числе,– за MS EXCEL).

Использование ЭТ предоставляет пользователю (студенту, преподавателю) следующие основные преимущества по сравнению с применением электронных калькуляторов:

• 1)    возможность изображения графического решения организационно – управленческой задачи в форме графиков функций (в EXCEL – это «Мастер диаграмм») как: а) от одной, так и б) от двух переменных [4], [8], [10], [11];

• 2)    возможность реализации прогнозирования на основе метода наименьших квадратов средствами как: а) подпрограмм (встроенных «функций» ЭТ), обеспечивающих матричные вычисления, так и: б) подпрограмм, надстроенных (в EXCEL – это «Добавить линию тренда» [16]) над программой автоматического расчёта и рисования графиков функций, а также

• 3)    дополнительные пакеты подпрограмм (которые надо предварительно распаковать) статистических расчётов (в EXCEL – это «Пакет анализа») [16] и численной оптимизации (в EXCEL – это «Поиск решения») [1], [11], [13], [16].

Использование программ численной оптимизации ЭТ, (в частности, программы «Поиск решения») предполагает, конечно, более высокий уровень не только 1) владения электронными таблицами, но и 2) математической подготовки. Хотя в учебном плане подготовки экономистов-ба- калавров нашего университета имеется соответствующая дисциплина («Методы оптимальных решений»), для бакалавров-менеджеров она (в явном виде) отсутствует. Поэтому в данной статье, ориентированной в первую очередь на студентов-менеджеров, возможности, предоставляемые студенту для выполнения письменных работ программой «Поиск решения», не рассматриваются.

Ещё более высокий уровень пользования табличными процессорами предполагает возможность составления компьютерных программ на специальном языке высокого уровня, встроенном в среду электронных таблиц [2], и в настоящей статье также не рассматривается.

Ориентация автора настоящей статьи на:

• 1)    круг рассматриваемых в письменных работах студентов-менеджеров предметных задач и математических методов их решения,

• 2)    уровень математической подготовки студентов, обусловили выбор для рассмотрения двух средств электронно-табличного моделирования (в EXCEL):

• а)    программы поддержки «деловой» графики – «Мастер диаграмм» и

• б)    программы «Корреляция» из «Пакета анализа».

Средство рисования графиков функций «Мастер диаграмм» («Chart Wizard») применимо во много большем числе разнообразных экономико-управленческих задач, нежели программа «Корреляция» (см. табл. 2), а поэтому, естественно, начать именно с демонстрации его возможностей.

В качестве первого примера возможностей «Мастера диаграмм» EXCEL имеет смысл рассмотреть результат построения матричной диаграммы «Свойства продуктов – сегменты рынка». Постановка и решение этой важной задачи (сегментации рынка) средствами программы «КАРЛ» (ещё в середине 1990-х годов в операционной системе MS DOS) представлены в учебном пособии [18].

На рис. 1 предъявлен тот же (с другими обозначениями) результат (ср. [18], с. 244), полученный автором настоящей статьи в среде EXCEL.

В целях демонстрации огромных возможностей «Мастера диаграмм» имеет смысл рассмотреть графическое решение технической задачи оптимального управления (минимального быстродействия) в среде EXCEL. Своеобразие этого графического решения (идея которого заимствована автором данной статьи из [5]) состоит в том, что графики функций составлены из отдельных маркеров (точек), из-за большого числа которых возникает эффект непрерывных линий.

В качестве частного случая задачи оптимального (минимального) быстродействия обычно рассматривают следующий пример. Перевести спутник на космической орбите из текущего состояния, обозначаемого двумя координатами { % ] ( t ) x ₂( t ) } в положение, принимаемое как начало координат {0; 0} , за минимальное время, где переменная x ₂ обозначает скорость изменения координаты x ₁ (расстояния центра массы спутника на околоземной орбите от нуля).

Уравнение состояния (уравнение динамики, уравнение движения) данной системы управления выглядит следующим образом [9]:

"x ) дt ax2_ IdtJ о о

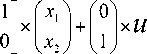
Из курса дифференциальных уравнений известно, что две группы решений этой системы дифференциальных уравнений второго порядка (двух переменных) имеют следующий вид:

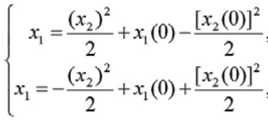
если u = l если u = — 1

Если даны конкретные начальные значения обеих координат { x Д0) x ₂ (0) } , то, подбирая различные значения постоянной «С» можно в двумерном пространстве состояний (называемой по традиции также фазовой плоскостью) данной системы управления изобразить её фазовый портрет, в данном случае – два множества графиков, определяемых видом решений (2).

Графическое решение задачи оптимального быстродействия можно получить, применяя компьютерную программную систему для моделирования систем управления SIMULINK, работающую в среде пакета MATLAB [17]. Однако, для этого необходимо, чтобы:

• 1)    и пакета MATLAB и встроенный в него программный продукт SI-MULINK были установлены в компьютерных классах вуза;

• 2)    и студенты, и преподаватели затратили время на овладение, как интерфейсом указанных программных средств, так и приёмами построения графиков в среде SIMULINK.

  

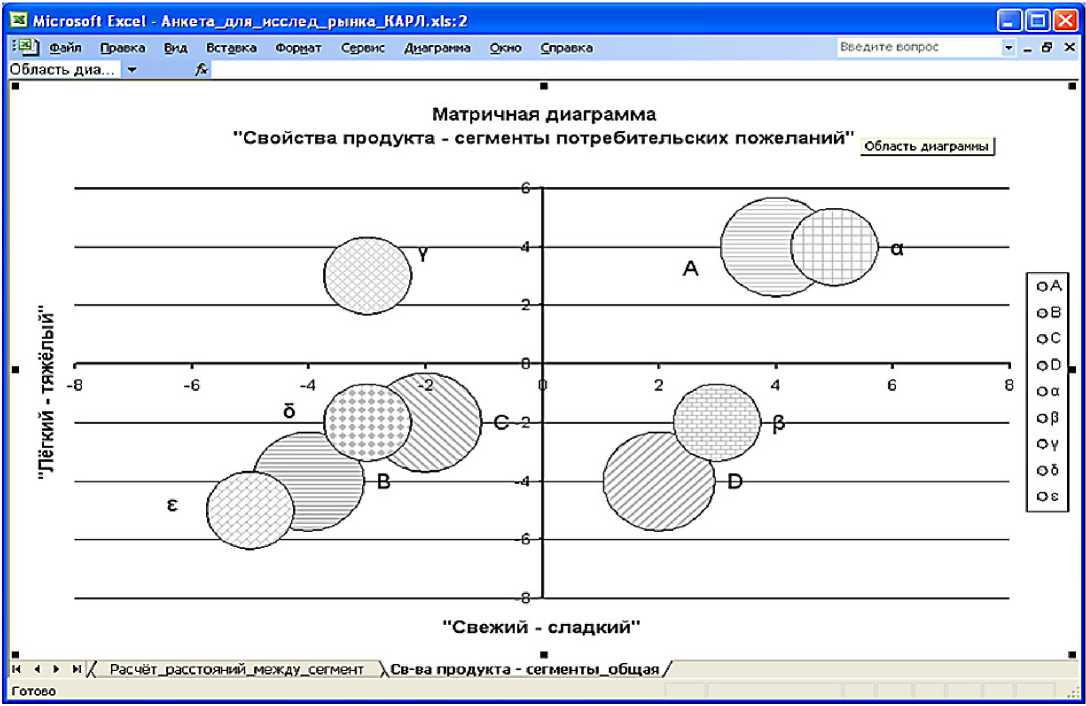
  Рис. 1. Совмещение продуктовых и потребительских сегментов на диаграмме «Свойства продуктов (от «А» до «D») – сегменты рынка (от « ά » до « ε »)».

  
  

Между тем, табличный процессор EXCEL позволяет студенту на основе известного решения системы дифференциальных уравнений второго порядка, а также начальных значений обеих координат изобразить фазовый портрет исследуемой системы управления.

В среде EXCEL удобно реализовывать построения фазовых портретов исследуемой системы управления с помощью параметрически заданных кривых. Применительно к рассматриваемому примеру это означает, что решение (2) надо представить как x ₁ (t), так x ₂ (t) в форме явной зависимости от параметра t (от времени).

t2

1 х₁ = — + tx x₂(0) + x,(0); х_г = t + х₂(0\если u = 1

(3) t²

• X] -н/хх₂(0) + х₁(0);х₂ = —t + x₂(O), если u = —1

Удобство параметрической формы решения системы дифференциальных уравнений второго порядка состоит в том, что параметру t можно присваивать легко вычисляемые значения, причём образующие арифметическую прогрессию (т.е. изменяемые с равным шагом).

Ниже приведено начало процесса подготовки данных для рисования фазового портрета исследуемой системы управления при изменении параметра от нуля до 2,84 с шагом, равным 0,02. В случае параметрического задания кривых график функций рисуют по точкам. На рисование каждой параболы, определяемой формулой (3), в этом случае требуется 143 точки.

В табл. 3 представлено начало процесса подготовки данных для последующего рисования графиков парабол, согласно формуле (3). Значения x ₁ (t) и x ₂ (t) вычислены для основного случая, когда в верхнем уравнении x ₁ (0) изменяется от -1 до 3 (с шагом, равным 1), а в нижнем уравнении x ₁ (0) изменяется от 1 до -3 (также, с шагом, равным 1). Это требует 715 точек (143 точки по 5 раз).

На рис. 2 показан фазовый портрет системы управления космически аппаратом, соответствующий формуле (3). Видно, что в то время, как координата положения x ₁ (t) изменяется на единицу, координата скорости x ₂ (t) изменяется на величину 2,84 {от -1,42 до 1,42 и, соответственно, в обратном направлении}.

Решениями примера, т.е. траекториями, переводящими космический аппарат (спутник) в точку начала координат (то есть в желаемую точку при нулевой скорости), являются только те две (по одной из каждого семейства кривых), которые содержат точку {0; 0} [9].

В статье [12] отмечены основные методические недостатки, часто обнаруживаемые в тексте выпускной квалификационной работы (ВКР) будущего менеджера. В настоящей статье это рассмотрение продолжено для двух типовых задач подготовки управленческих решений, нередко вычисляемых ошибочно.

План дальнейшего рассмотрения в данной статье методологических важных экономических примеров представлен в табл. 4.

2.    Формирование матричной диаграммы БКГ с помощью пузырьковой диаграммы «Мастера диаграмм» EXCEL.

Таблица 3. Подготовка данных для изображения фазового портрета системы управления.

«SjyQjjyyiyyyyjjyjyyjggyyg^		^Г№№4
SJ Оанп Правка Сид Вставка Формат Серок Данные Окно Справка А4 Е     Л	Введите вопрос	• - в х

А В с D Е F G Н 1 3 Значения оптимального управления U = 4 1 1 1 -1 -1 -1 5 Хю Ха хг= t* хм Хю Ха Х1--(Р)В+ Гхг9+х„ X2=-t + х„ 6 0 -1.42 •1,000 -1.420 1 1.42 1.000 1,420 7 0,02 -1,42 -1,028 -1,400 1 1,42 1,028 1 ,400 8 0.04 - 1 -1.42 -1,056 -1.380 1 1.42 1.056 1 .380 9 0,06 -1.42 -1 ,083 -1,360 1,42 1.083 1 ,360 10 0,08 -1.42 -1,110 -1,340 1 1,42 1.110 1 .340 11 0.1 -1 -1.42 -1,137 -1.320 1.42 1.137 1.320 12 0,12 -1 -1.42 -1,163 -1.300 1 1.42 1.163 1 .300 13 0,14 -1 -1.42 -1,189 -1.280 1 1.42 1.189 1 .280 14 0,16 -1.42 -1,214 -1.260 1.42 1.214 1 .260 15 0,18 -1 -1,42 •1 ,239 •1,240 1 1,42 1.239 1,240 16 0.2 -1,42 • 1,254 -1,220 1.42 1.264 1.220 17 0,22 -1 -1,42 -1,288 -1,200 1 1,42 1.288 1 ,200 18 0.24 -1.42 -1,312 -1.180 1 1.42 1312 1 ,160 19 0,26 -1 -1 .42 -1,335 -1.160 11 1.42 1335 1 ,160 20 0.28 - 1 -1.42 -1,358 -1.140 11 1.42 1.358 1,140 21 о,3 -1.42 -1 .381 -1,120 1 1.42 1.381 1 ,120 22 0,32 -1.42 -1,403' -1.100 1 1.42 1.403 1 .100 23 0.34 -1.42 •1,425 -1.080 1.42 1.425 1 .080 24 0,36 -1,42 -1 ,446 -1,060 1 1,42 1.446 1 ,060 25 0,38 -1.42 • 1,467 -1.040 1.42 1.467 1 ,040 26 0,4 -1,42 *1,488 -1,020 1 1.42 1.488 1 .020 27 0,42 -1 -1.42 -1.508 -1.000 1 1.42 1.508 1 .000 28 0,44 -1.42 -1.528 -0,980 1 1.42 1.528 0,980 29 0.46 -1.42 -1,547 -0.980 11 1.42 1.547 0.960 30 0,48 - 1 -1.42 -1 ,566. -0.940 1 1.42 1.566 0,940 31 0,5 - 1 -1.42 -1,585 -0,920 1 1,42 1.585 0,920 32 0.52 -1.42 -1 .603 -0.900 11 1.42 1.603 0.900 33 0.54 -1.42 -1,621 -0,880 1 1.42 1.621 0,880 34 0,56 -1.42 -1.638 -0,860 1 1.42 1.638 0,860 35 0,58 • 1.42 • 1,655 •0.840 1 1.42 1.655 0,840 36 0.6 •1,42 •1,672 -0,820 1 1.42 1.672 0,820 и , , и\Решение_оптим_быстродейств__ДДНа/ Диаграмма1_фазоеый_портрет /    |<|                                   '          [> |

Готово

Таблица 4. План дальнейшего рассмотрения экономических примеров

№ задачи	Название задач из области управленческой экономики, решаемых соответствующими средствами EXCEL.	Правильное решение	Ошибочное решение в ВКР
1.	Решение и графическая визуализация матричной диаграммы БКГ.	Пример 1.1. { в [3], [4]}	Пример 1.2.
2.	Вычисления матрицы коэффициентов парной корреляции.	Пример 2.1. { в [16]}	Пример 2.2.

Таблица 5. Фрагмент начальных данных для визуализации матричной диаграммы БКГ [3].

Наименование продукции	Выручка		Доля рынка
	1995	1996	фирмы	конкурента
Фотоаппараты для РФ и СНГ	2900	2500	0,34	0,17
Фотоаппараты для 3-го мира	590	649	0,33	0,21
<…>	<…>	<…>	<…>	<…>
Оптические приборы для ВПК	900	400	0,02	0,04

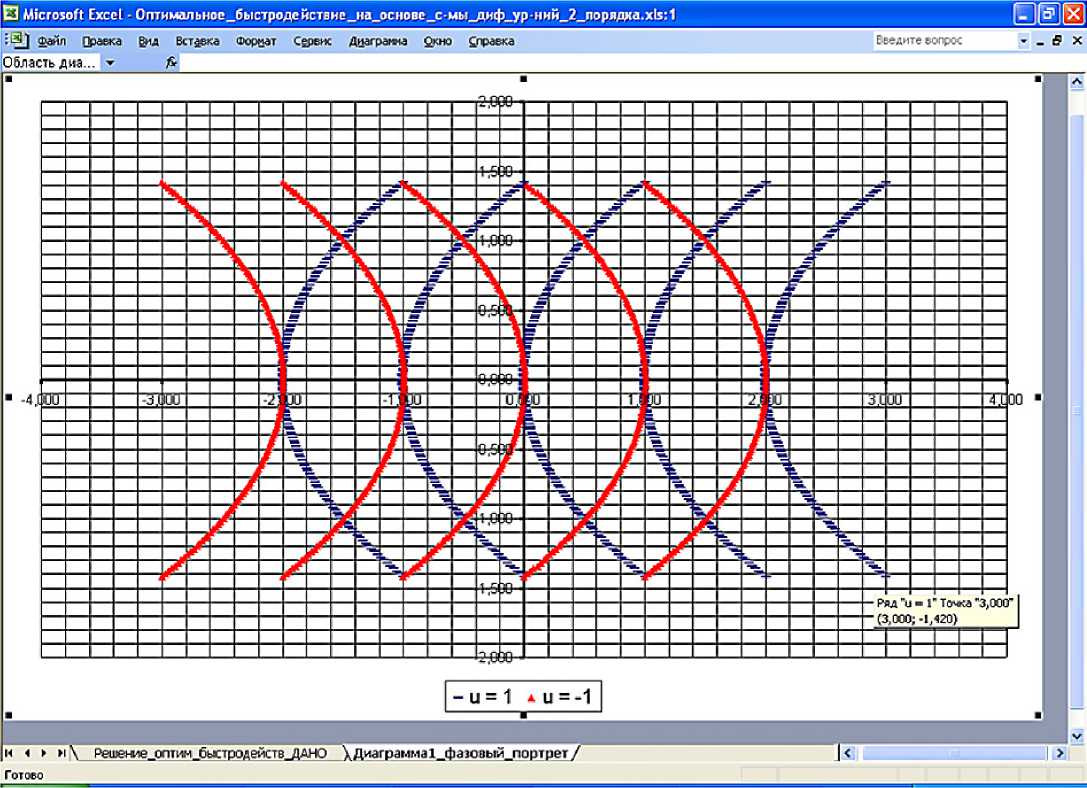
Рис. 2. Фазовый портрет системы управления космическим аппаратом, соответствующий формуле (3).

Таблица 6. Вычисления ОДР, индекса роста рынка и долей товара в общей выручке [4].

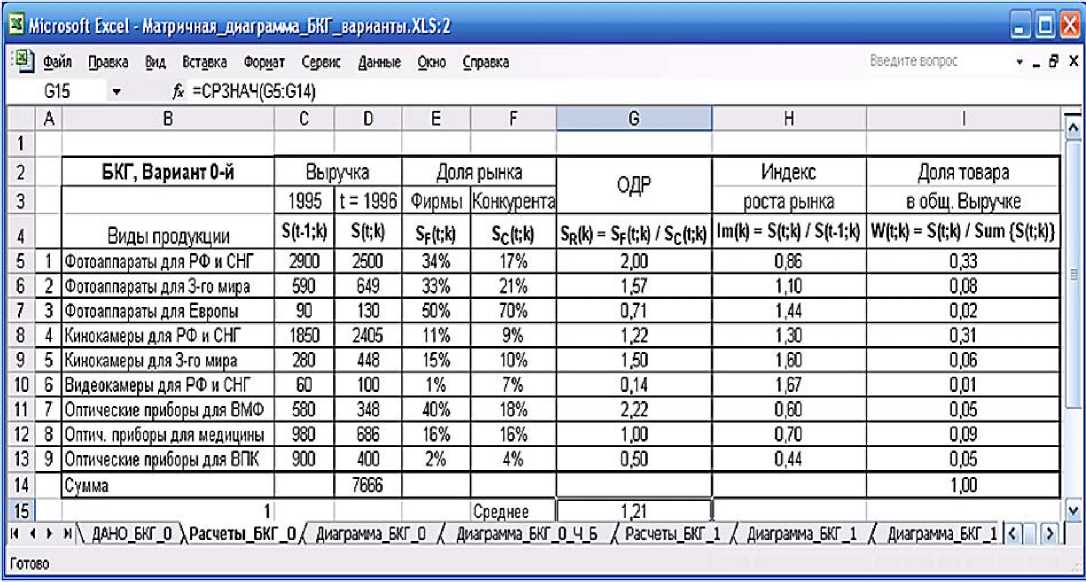
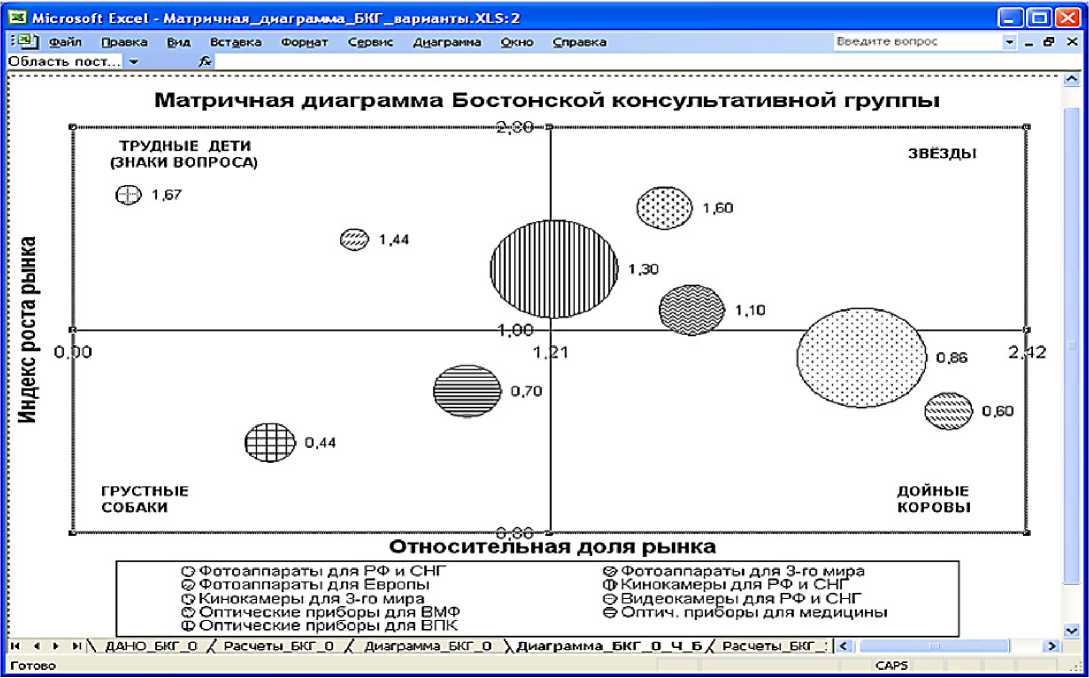
Рис. 3. Изображения размеров выручки (прибыли)

по каждой товарной группе на плоскости «Относительная доля рынка – индекс роста рынка» [4].

Как известно, этап жизненного цикла продукта на матричной диаграмме БКГ формируется по двум показателям. По горизонтальной оси откладывается доля, занимаемая всяким выпускаемым фирмой товаром на рынке отно-си-тельно доли сильнейшей (занимающей максимум рынка по этому товару) фирмы-конкурента. По вертикальной оси показывают индекс темпа роста рынка (отрасли). Размер радиуса круга соответствует доле занимаемой любым товаром, выпускаемым фирмой, в общей сумме её продаж на разных рынках.

Пример 1.1. [3], [4]. Дано. Предприятие, специализирующееся на выпуске фотоаппаратов, кино- и видеокамер, высокоточных оптических приборов, сбывает продукцию в России, СНГ, развивающихся странах и Западной Европе. Табличная структура начальных данных представлена в табл. 5 (фрагмент).

В табл. 6 полностью предъявлены начальные данные и необходимые вычисления для всех девяти товарных позиций. На рис. 3 показана диаграмма БКГ, построенная по данным 1-го примера.

Для наглядной демонстрации возможных крупных методических ошибок при формировании матричной диаграммы БКГ, совершаемых студентами-выпускниками можно рассмотреть пример 1.2, взятый из ВКР, выполненной в МОГИ, в 2011-2012 учебном году.

1. ПРИМЕР 1.2. ОН ИМЕЕТСЯ В § 3.1 ЭТОЙ ВКР, ОЗАГЛАВЛЕННОМ: «ПРОЕКТИРОВАНИЕ КОМПЛЕКСА МЕРОПРИЯТИЙ ПО РАЗРАБОТКЕ СТРАТЕГИИ И УПРАВЛЕНИЕ ПРОДУКТОВЫМ ПОРТФЕЛЕМ». ПОСЛЕ ПОДЗАГОЛОВКА «РАЗРАБОТКА СТРАТЕГИИ УПРАВЛЕНИЯ ПРОДУКТОВЫМ ПОРТФЕЛЕМ. АНА-

ЛИЗ ПРОДУКТОВОГО ПОРТФЕЛЯ» АВТОРОМ ВКР, НАБРАН СЛЕДУЮЩИЙ ТЕКСТ.

«По результатам проведения натурально-стоимостного анализа продуктового портфеля ОАО «Вимм-Билль-Данн» определены доли торговых марок в общем объеме продаж Компании: Чудо – 22,2%, Веселый молочник – 8,7%, Домик в деревне – 11,8%, 33 коровы – 0,1%, Рыжий АП – 1,0%, Neo Beauty, Имунеле, 2 Bio, Bio Max – 9,2%, Фругурт – 1,4%б другие бренды и небрендовые продукты – 45,6%.

<…> Рост рынка потребления для каждого бренда, с учетом темпа роста потребления каждой категории продуктов, выпускаемых под единым брендом: Чудо – 18%, Веселый молочник – 5%, Домик в деревне – 12%, 33 коровы – 5%, Рыжий АП – 5%, Neo Beauty, 2 Bio, Bio-Max, Имунеле – 20%б Фру-гурт – 7%, другие бренды и небрендовые продукты – 12% .» (конец цитаты).

По выше указанным данным студентка – автор ВКР, предъявляет следую-щую матричную диаграмму Бостонской консультативной группы, якобы построенную на основе соответствующих вычислений.

Эта диаграмма БКГ, скопированная через буфер обмена WINDOUS из файла ВКР, набранного в WORD, состоит из двух слоёв: 1) импортированного в WORD рисунка двух осей с подписями и 2) наложенными на них названиями торговых марок молочных продуктов (без кавычек). На основании этой диаграмма БКГ автор ВКР предъявляет в § 3.2 результаты после применения новой типичной стратегии перераспределения ресурсов от «грустных собак» и «дойных коров» к «звёздам» и «трудным детям».

В процессе рецензирования этой ВКР автор настоящей статьи пытался рассчитать и нарисовать в среде EXCEL со-

Таблица 7. Вычисления ОДР, индекса роста рынка и долей товара в общей выручке для примера 2.

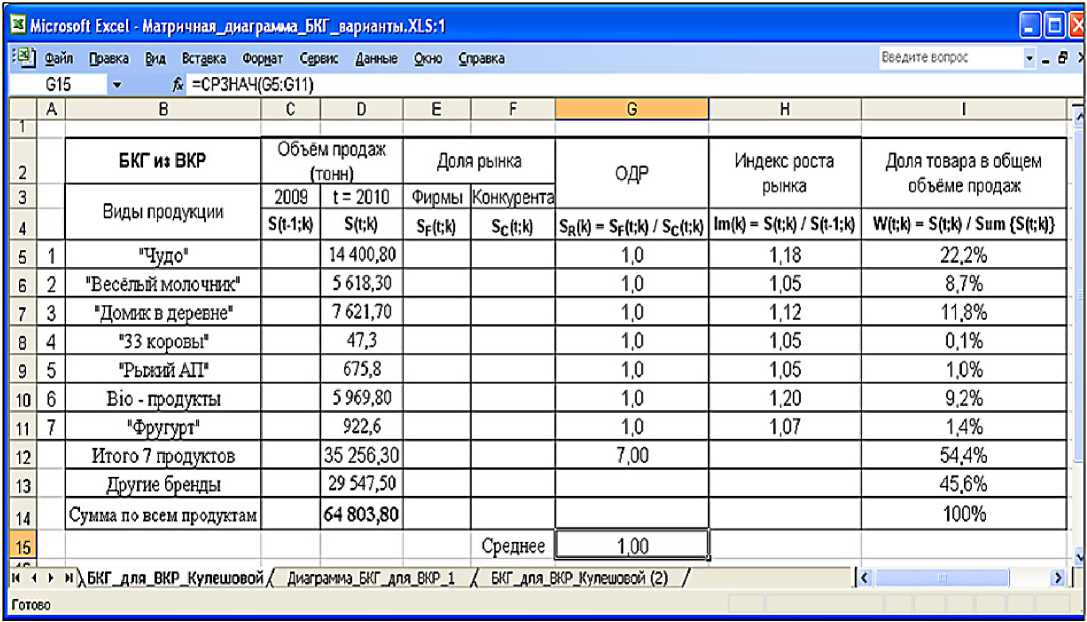
ответствующую матричную диаграмму БКГ, чтобы сравнить её с той, что воспроизведена на рис. 4. Эта попытка представлена в табл. 7.

Как видно, из табл. 4, данные по SF[k] – доле выручки фирмы в общей выручке на рынке за текущий год, как и данные по SС[k] – доле выручки главного конкурента фирмы за текущий год – в табл. 7 отсутствуют.

Следовательно, невозможно применить формулу для вычисления значений относительной доли рынка (ОДР) по k-му виду продукции:

SR[k] = SF[t;k] / SC[t;k],                 (4)

Веселый молочник

Рыжий АП

Другиебренды

Чудо

Домик в деревне

Зпоэда

Дойная коропа

300% высокая

Bio - продукты ( Neo Beauty, 2 Bio, Bio Max)

Фругур т 33 коровы

Собака

1ОО%

3 0% низкая

Рис. 4. Матричная диаграмма БКГ, предъявленная в рецензируемой ВКР.

Если бы студентка – автор ВКР, попыталась нарисовать матричную диаграмму БКГ средствами «Мастер диаграмм» EXCEL, то у неё получилась бы пузырьковая диаграмма, аналогичная той, что показана на рис. 5.

Согласно принципу «недостаточного обоснования» Лапласа, если данные компонент вектора отсутствуют, то надо считать их равными. Поэтому все значения ОДР должны быть равны середине отрезка горизонтальной оси, например, SR[k] = 1, а отсюда следует, что все «пузырьки» выстраиваются строго вдоль вертикальной оси. Следовательно, вместо привычного распределения продуктов по четырём областям матричной диаграммы БКГ, у автора ВКР, на самом деле, должно было получиться распределение этих продуктов только по двум областям вдоль вертикальной оси. В этом случае исчезает разница между продуктами – «звёздами» и продуктами – «трудными детьми», а также между продуктами – «дойными коровами» и продуктами – «грустными собаками». Поэтому сравнение автором ВКР двух стратегий: «ничего не менять» и «перераспределить ресурсы между продуктами разных этапов жизненного цикла» является не соответствующим действительности.

В то же время, честная попытка нарисовать матричную диаграмму БКГ средствами «Мастер диаграмм» EXCEL предостерегла бы автора ВКР от наукообразной фантастики.

Использование ЭТ, в частности EXCEL, предоставляет пользователю (студенту) возможность организации почти параллельных вычислений – частному случаю распараллеливания работ, к чему всегда должен стремиться менеджер.

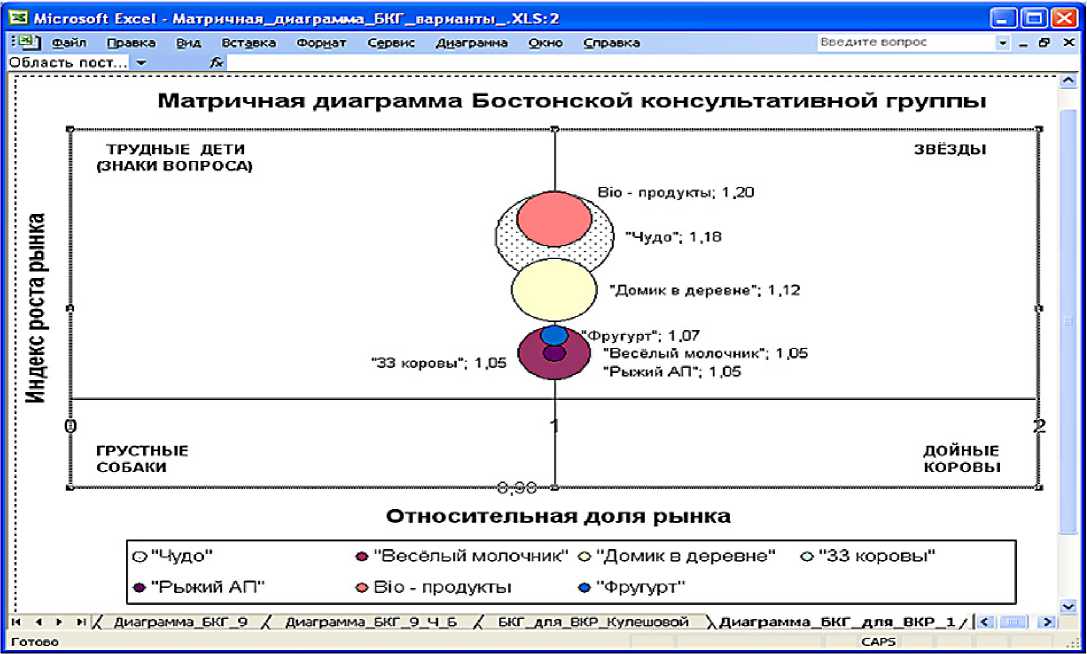
Рис. 5. Матричная диаграмма БКГ примера 1.2, сформированная на основе начальных данных, предъявленных в рецензируемой ВКР.

Этот подход показан ниже на примере расчёта матрицы коэффициентов парной корреляции с помощью «Пакета анализа» («Data Analysis») EXCEL.

3.    Расчёт матрицы парных коэффициентов корреляции с помощью «Пакета анализа» EXCEL.

Форма ответа этих параллельных (точнее – квазипарал-лельных, так как вычисления происходят, всё-таки, последовательно, но настолько быстро, что выдаются все сразу в виде матрицы) вычислений называется «матрица коэффициентов парной корреляции», имеющая одну из двух разновидностей, в частности:

Из курсов «Эконометрика» и «Статистика» известно, что

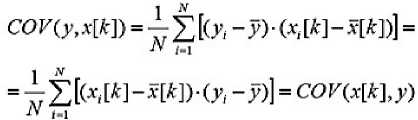
	y	x 1	x 2	...	x N
y	1	R yx 1	R yx 2	...	Ryx N
x 1	Rx 1 y	1	R x 1 x 2	...	R x 1 xN	(5)
x 2 ...	R x 2 y ...	R x 2 x 1 ...	1 ...	... 1	R x 2 xN ...
_ x N	R x N y	R xNx 1	R xN x 2	...	1 J

Поэтому

СОРЧ^хЩ) _ ОЩЬ)

- ^.]y

(7),

а отсюда, следует, что матрица коэффициентов парной корреляции есть симметричная матрица (относительно главной диагонали), т.е. для любых двух её элементов R x [ k ] = R x [ k ] y и R x [ i ] x [ k ] = R x [ k ] x [ i ]

Из симметричности матрицы коэффициентов парной корреляции, в свою очередь, следует, что для её изображения достаточно показать её часть: 1) либо верхнюю (правую) треугольную матрицу, 2) либо левую (нижнюю) треугольную матрицу.

В табличном процессоре EXCEL выбран вариант показа левой (нижней) треугольной части матрицы коэффициентов парной корреляции. Для вычисления матрицы коэффициентов парной корреляции в EXCEL применяют специальное дополнительное средство, называемое «Пакет анализа».

Пример 2.1. (из книги И.В. Орловой [16], c. 108 – 112).

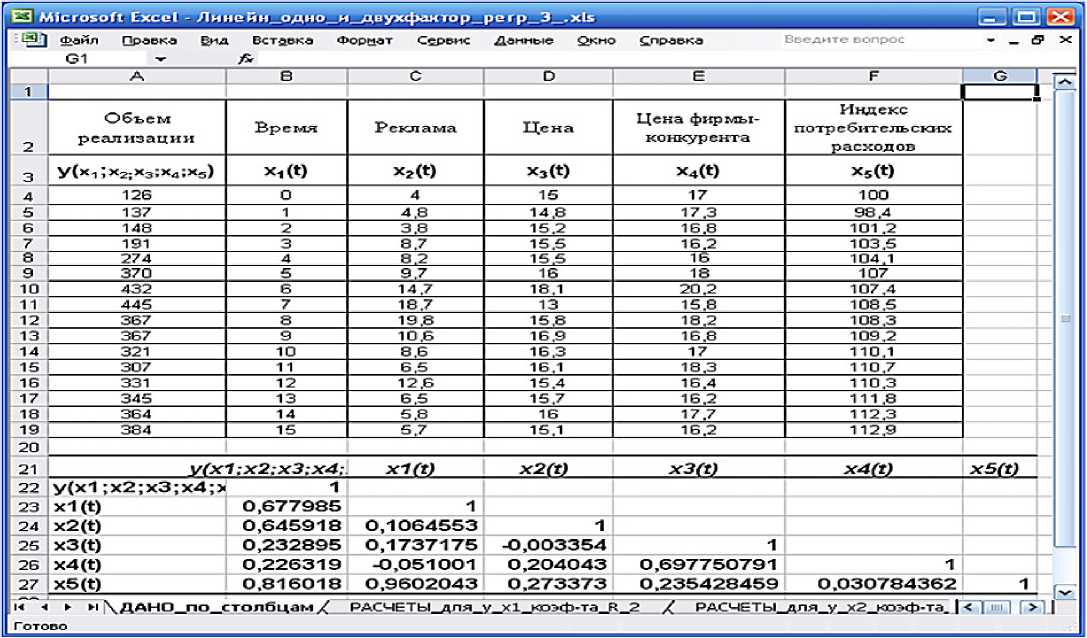
Дано. В табл. 5 показана табличная (дискретная) зависимость между пятью независимыми факторными признаками: x ₁ (время), x ₂ (реклама), x ₃ (цена), x ₄ (цена фирмы-конкурента), x ₅ (индекс потребительских расходов) и результативным признаком, обозначенным y(x ₁ ;x ₂ ;x ₃ ;x ₄ ;x ₅ ) (объём реализации).

Найти факторные признаки, которые могут быть отброшены:

• а)    либо из-за слабого влияния на результативный признак,

• б)    либо из-за сильного взаимного влияния с каким-либо другим факторным признаком, который сильнее влияет на результативный признак.

Таблица 8. Начальные данные о дискретной зависимости от 5 факторных признаков [16].

Объем реализации	Время	Реклама	Цена	Цена фирмы-конкурента	Индекс потребительских расходов
y(x1;x2;x3;x4;x5)	x1	x2	x3	x4	x5
126	0	4	15	17	100
137	1	4,8	14,8	17,3	98,4
148	2	3,8	15,2	16,8	101,2
191	3	8,7	15,5	16,2	103,5
274	4	8,2	15,5	16	104,1
370	5	9,7	16	18	107
432	6	14,7	18,1	20,2	107,4
445	7	18,7	13	15,8	108,5
367	8	19,8	15,8	18,2	108,3
367	9	10,6	16,9	16,8	109,2
321	10	8,6	16,3	17	110,1
307	11	6,5	16,1	18,3	110,7
331	12	12,6	15,4	16,4	110,3
345	13	6,5	15,7	16,2	111,8
364	14	5,8	16	17,7	112,3
384	15	5,7	15,1	16,2	112,9

Таблица 9. Результат вычисления матрицы коэффициентов парной корреляции [16] в режиме «Корреляция» (Correlation) из «Пакета анализа» EXCEL.

Решение Можно разделить силу влияния (тесноту связи) как 1) факторных признаков на результативный признак y, так и 2) факторных признаков между собой по укрупнённому критерию, основанному на системе следующих неравенств:

• 1)    если R <  0,3 , то зависимость слабая;

• 2)    если 0,3 <  R < 0,7 , то зависимость средняя;

• 3)    если 0,7 <  R < 1 , то зависимость сильная или тесная.

План (идея) решения состоит в реализации трёх этапов.

• 1.    Вычислить матрицу коэффициентов парной корреляции,

• 2.    Проверить есть ли среди факторных признаков такие, у которых R < 0,3 и, если «да», то исключить их из дальнейшего рассмотрения.

• 3.    Проверить есть ли среди факторных признаков такие, у которых 0,7 <  R x [ i ] x [ k ] < 1 и, если «да», то затем проверить какой сильнее влияет на результативный признак, т.е. сравнить между собой два значения R _{yx [ i ]} и R _{yx [ k ]} :

• а)    если R _{yx [ i ]} ≥ R _{yx [ k ]} , то надо отбросить k –й признак,

• б)    если R _{yx [ i ]} ≤ R _{yx [ k ]} , то надо отбросить i –й признак.

Результат 1-го этапа выполнения этого плана представлен в табл. 9.

Из табл. 9 видно, что R _{yx [3]} ≤ 0,3, а также R _{yx [4]} ≤ 0,3. Поэтому можно отбросить факторные признаки x ₃ (цена) и x ₄ (цена фирмы-конкурента). Тогда остаются три признака: x ₁ (время), x ₂ (реклама) и x ₅ (индекс расходов).

Так как 0,7 ≤ R _{x [1] x [5]} ≤ 1, то тесно связаны между собой x ₁ (время) и x ₅ (индекс потребительских расходов). Поэтому, один из них можно отбросить.

Сравнение между собой значений Ryx[1] и Ryx[5] показывает, что Ryx[1] ≤Ryx[5]. Значит, надо отбросить 1–й признак (время).

Таким образом, остаются два значимых признака: x ₂ (реклама) и x ₅ (индекс потребительских расходов), т.е. можно подбирать уравнение (формулу) регрессии для y(x ₂ ;x ₅ ). После переименования факторов, например, в виде x ₁ = x ₅ задача может быть записана в стандартной форме.

Пример 2.2. (неправильного расчёта парных коэффициентов корреляции в ВКР, выполненной в МГИ, в 2011-2012 учебном году.)

«Для корреляционного анализа используем данные, представленные в таблице 10, и рассчитаем степень тесноты их парных связей.

Таблица 10. Корреляционная таблица

Год	Коэф. текучести	Производитель-ность	Мотивирован-ность	Эф. от увеличен. производ-ти
	Х1*	Х2*	Х3*	Х4*
2010 г IV кв.	0,11	40,70	2,85	1424,4 (1,4тыс)
2011 г I кв.	0,06	60,69	3,31	2245,4 (2,2тыс)

Запишем полученные результаты в виде корреляционной матрицы

	" 1	-0,34	0,56	0,13
	-0,34	1	1	1
R =	0,56	1	1	1
	_ 0,13	1	1	1

Проведенное выше исследование показало, что выбранные для сравнения переменные коррелируют. И изменение значения одной переменной Х1 влечет за собой пропорциональное изменение значения Х2.

А значит, повышение мотивированности работников сборочно-монтажного цеха и удовлетворенности своим трудом привело к уменьшению текучести кадров, повышению производительности труда и эффекта от увеличения производительности» (конец цитаты).

В практикуме [7] приведена следующая полезная информация.

«При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов, их тесной линейной связанности.

• <…> Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами .

Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы Rx[.]x[k] (x.^ xk) были бы равны нулю. Так, для включающего три объясняющих переменные уравнения y = a 0 + b1 x x1 + b 2 x x 2 + b3 x x 3 + e матрица коэффициентов корреляции между факторами имела бы определитель, равный единице:

	R x 1 x 1	R x 1 x 2	R x 1 x 3		1	0	0
Det\R\ =	R x 2 x 1	R x 2 x 2	R x 2 x 3	=	0	1	0	= 1
	R	R	R		0	0	1
	x 3 x 1	x 3 x 2	x 3 x 3

• <…> Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадёжнее результаты множественной регрессии.

И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов» (конец цитаты).

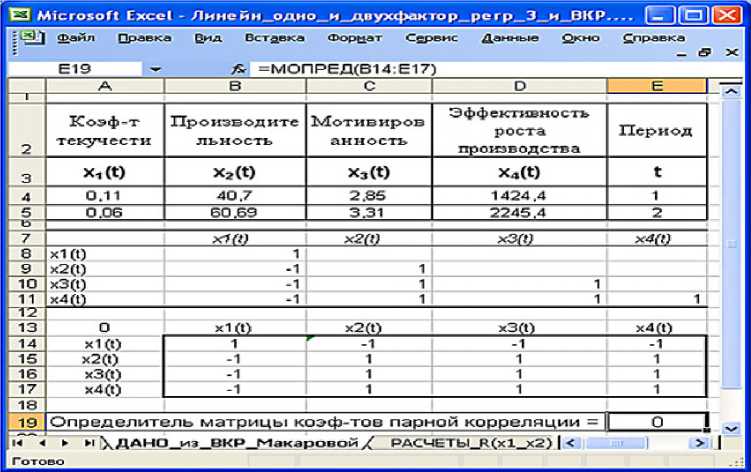
Готовя рецензию, автор этой статьи честно ввёл данные (из табл. 10) в расчётный блок ячеек одного их своих файлов, отличающихся друг от друга практически только примерами, и получил результат, показанный в табл. 11.

Из табл. 11 видно, что получился вариант

1 -1 -1 -1 Det R = -1 1 1 1 = 0, (8) -1 1 1 1 -1 1 1 1 что, согласно [7], означает полную ненадёжность последующих выводов.

Причина получения в ВКР вырожденной матрицы коэффициентов парной корреляции (8) заключена в том, что студентка-выпускница ограничилась только двумя точками измерений. Для двух точек измерений (независимо от числа факторов) можно доказать, что все коэффициенты корреляции любой, отдельно взятой пары двух факторов всегда по абсолютной величине равны единице.

Даже не зная заранее этого результата, студентка – автор ВКР, натолкнулась бы на него, если бы попыталась честно выполнить вычисления парных коэффициентов корреляции в среде EXCEL:

• 1)    сначала с помощью «Пакета анализа», а затем и

• 2)    проведя подробные вычисления на листе рабочей книги последовательно (попарно), в полуавтоматическом режиме.

Это избавило бы её от необоснованных выводов.

Таким образом, преимущества применения ЭТ над калькуляторами при выполнении письменных работ будущими менеджерами и экономистами трудно переоценить.

Таблица 11. Результат вычисления матрицы межфакторной корреляции 4-х признаков в режиме «Корреляция» («Correlation») из «Пакета анализа» EXCEL.