Преобразование краевой дислокации высокого порядка в набор оптических вихрей (винтовых дислокаций)

Астигматические преобразования лазерных пучков в оптике хорошо известны. Первой работой по астигматическому конвертору была работа Абрамоч-кина и Волостникова [1], в которой показано, как с помощью астигматического конвертора безвихревой пучок Эрмита–Гаусса (ЭГ) преобразуется в вихревой пучок Лагерра–Гаусса (ЛГ). В этой работе пучок Эрмита–Гаусса ( n , m ) преобразуется в моду Лагерра– Гаусса ( n , m – n ) всего с помощью одной цилиндрической линзы. Позже во многих работах изучалось преобразование различных лазерных пучков с помощью астигматических преобразований. Так, в [2, 3] изучалось прохождение пучка Эрмита–Гаусса через 4×4 оптическую систему, в том числе с астигматизмом. В [4] рассмотрено прохождение пучков Эрмита– Лагерра–Гаусса через астигматический модовый конвертор. В [5, 6] исследовалась фокусировка астигматической линзой оптического вихря высокого порядка. Преобразования астигматического sin-Гауссова пучка в нелинейной среде рассматриваются в [7]. В [8, 9] исследуется астигматическое модовое преобразование внутри лазерного резонатора. Оптические эллиптические Гауссовы вихри с астигматической фазой рассматривались ранее в [10, 11]. В [10] рассматривалось преобразование пучка Эрмита–Гаусса порядка (0, n ) с помощью повернутой цилиндрической линзы. В [11] рассмотрен модовый пучок, у которого канонический оптический вихрь с ТЗ, равным n , внедренный в эллиптический астигматический Гаус-

сов пучок, сохраняется при распространении и не расщепляется на простые оптические вихри. В [12] рассмотрено распространение эллиптических оптических вихрей. Измерять топологический заряд оптического вихря с помощью астигматического преобразования предложено в [13]. В [14] рассмотрен астигматический вихревой пучок Эрмита–Гаусса.

С другой стороны, известны работы, в которых исследуется поведение винтовых [15] и краевых дислокаций в оптических системах. Так, в [16] изучалась эволюция при распространении смеси краевой (осевой) и винтовой дислокаций. В этой работе показано, что комбинированный оптический вихрь имеет дробный топологический заряд. В [17–20] исследуется взаимодействие оптического вихря (винтовой дислокации) и краевой поперечной дислокации (линии нулевой интенсивности), внедренных в Гауссов пучок. В этих работах показано, что это взаимодействие приводит к расщеплению краевой дислокации и формированию дополнительных оптических вихрей.

Из рассмотренного краткого обзора работ следует, что астигматического преобразования краевой дислокации не рассматривалось. В данной работе мы теоретически и численно показали, что вертикальная краевая дислокация n-го порядка, внедренная в перетяжку Гауссова пучка, после цилиндрической линзы, расположенной в перетяжке и повернутой на 45 градусов к осям, «распадется» на n изолированных нулей интенсивности (винтовых дислокаций), вокруг которых сформируются n эллиптических оптических вихрей с топологическим зарядом –1, лежащих на пря- мой, перпендикулярной краевой дислокации, и расположенных в точках, координаты которых являются корнями многочлена Эрмита n-го порядка.

1. Комплексная амплитуда поля с краевой дислокацией на двойном фокусном расстоянии

Рассмотрим краевую дислокацию, внедренную в перетяжку Гауссова пучка с астигматической фазой. То есть в плоскости перетяжки Гауссова пучка с краевой дислокацией n -го порядка, которая проходит через центр и совпадает с вертикальной осью, расположена идеальная тонкая цилиндрическая линза, образующая которой повернута в плоскости перетяжки на 45 градусов к осям координат. Комплексная амплитуда такого светового поля в начальной плоскости имеет вид:

E n =- w 71 + Y ² ( y ) ¹ a n .

x ⁿ

E ( x , y , z = 0) = —exp wⁿ

( x ² + y ² V-- w-"

^- "ikf ^{( x +} y ^{) 2} J , ⁽¹⁾

где k – волновое число света, w – радиус перетяжки Гауссова пучка, ( x, y ) – поперечные декартовы координаты и z – продольная координата вдоль оптической оси, f – фокусное расстояние цилиндрической линзы. Второе слагаемое в показателе экспоненты в (1) описывает распределение фазы цилиндрической линзы с параболическим профилем, расположенной под углом 45 градусов к осям x и y .

Наша цель – показать, что на горизонтальной оси x на двойном фокусном расстоянии от цилиндрической линзы сформируется n оптических вихрей с ТЗ –1.

Амплитуда светового поля (1) на расстоянии z =2 f , полученная с помощью преобразования Френеля, будет иметь вид:

Из общей формулы (3) следуют частные случаи. Пусть краевая дислокация имеет второй порядок и совпадает с осью η, тогда в выходной плоскости будет только два нуля на горизонтальной оси на расстоянии от центра, равном £ _1>2 = ± w (1 + y ² )^1/2 (V2 Y ) ^{- 1}. Это следует из того, что у многочлена Эрмита 2-го порядка всего два корня о _1>2 = ± 1/ V2. Краевая дислокация 3-го порядка даст на выходе 3 оптических вихря: один на оптической оси, а два других в точках с координатами: E i,2 =± w (1 + y ²)^1/2( y V2/3) ^{- 1}. Так как у многочл ена Эрмита 3-го порядка три корня: a ₀ 0, a _1j2 = ± V3/2 . И так далее.

Рассмотрим далее, какие оптические вихри формируются на двойном фокусном расстоянии для начального пучка (1). Из (2) следует, что вокруг корней многочлена Эрмита на горизонтальной оси сформируются эллиптические вихри с топологическими зарядами –1 и с эллиптической амплитудой вблизи нуля интенсивности:

^- i Yn = Р exp ( - i 0 ) .

Правая часть в (4) получена в полярных эллиптических координатах:

^ = Р cos 0 , П = Y^{- 1} p sin 0 .

E ( E , n , z = 2 f ) =

( - i ) n ^{+ 1} Y

~              ( n + 1)/2

2 ⁿ ( 1 + Y ² ) (   ) J

X

Эллиптический вихрь становится каноническим оптическим вихрем при условии γ = 1 ( z 0 =2 f ):

^- i n = p exp ( - i 0 ) ,                                (6)

а амплитуда светового поля (2) будет иметь вид (γ =1):

x exp

-

Y ² ( E ² +П ² )

V

w ²

( 1 + Y ² )

+

(    i n -1     1

E fE , n , z = z₀ = 2 f ) = ------- x

, ”         ^{0 J} / I 2 (3 n + 1)/2 I

+ 4(^2 +n2 )+ 'i' П | w2            w2 (1 + y 2 )J

x exp

f_ (£ + 42)

X

X H n

y ( E- i Yn ) wJ 1 + Y ²

где γ = z 0 /(2 f ), z 0 = kw ²/2. В (2) z 0 – длина Рэлея, H n ( x )– многочлен Эрмита. Из (2) следует, что у Гауссова пучка на двойном фокусном расстоянии изменился радиус перетяжки w ( z = 2 f ) = w = w ^{- 1}V1 + Y ² и появилась астигматическая фаза. Из (2) также следует, что при η =0 аргумент многочлена Эрмита становится действительной величиной. Приравнивая этот аргумент значениям корней многочлена H n ( a n ) = 0, получим координаты центров эллиптических оптических вихрей (винтовых дислокаций), лежащих на горизонтальной оси ξ:

X H n

2 w ² V

( ^- i n ) w41

+- ik - (^²

4 f ⁽^

X

Чтобы пучок (7) сохранял далее свою структуру (то есть стал модовым пучком) при дальнейшем распространении, надо на двойном фокусном расстоянии расположить еще одну цилиндрическую линзу, повернутую на 45 градусов к осям, с пропусканием exp [- ik ( E + n)² / (8 f )]. Эта линза скомпенсирует астигматическую фазу, которая присутствует в (7). Причем фокусное расстояние у этой цилиндрической линзы должно быть в 2 раза больше, чем у цилиндрической линзы в (1). Сразу после второй цилиндрической линзы вместо (7) получим:

n - 1

E (E, n, z = z0 = 2 f) = x ' -, M 0 J / I 2(3n+1)/2 I x exp

" ^{( E} 2 +n ² )

2 w ²

V

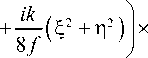
x H n

(^E- i n )

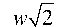
Пучок (8) является частным примером семейства структурно-стабильных пучков [4], которые распространяются, изменяя только масштаб и вращаясь. Пучок (8) с точность до обозначений совпадает с вихревым пучком Эрмита, рассмотренным в [14].

Из теории структурно-стабильных Гауссовых лазерных пучков [4] следует, что пучок с начальной амплитудой вида

E ( E , n , z = 0 ) =

= H n [a ( E± i n ) ] exp ( -P (^E 2 ⁺ n ² ) ) ,

где α и β – комплексные постоянные и Reβ >0, будет при распространении сохранять свою структуру, а изменяться только масштабно и вращаться. Это общее доказательство того, что пучок (8) тоже будет сохранять структуру при распространении.

2.    Орбитальный угловой момент

В этом параграфе мы получим выражение для нормированного орбитального углового момента пучка (1). ОУМ параксиального пучка находится по известным формулам [1]:

f f | d E ( x , y )     d E ( x , y ) V

Jz = Im    E (x, y) I x--y--------I dxdy, dy        dx

^{-f-f V                      1} (10)

f f

W = j j E ( x , y ) E ( x , y ) dxdy ,

-f

-f

где Im – мнимая часть числа, J z – ОУМ пучка, W – мощность пучка, E – комплексно сопряженная функция к функции E . Так как ОУМ пучка сохраняется, рассчитаем его в начальной плоскости. Подставим функцию (1) в (10) и получим простое выражение для нормированного на мощность ОУМ:

J z W

= -y n .

При γ = 1 ОУМ поля (1) совпадает с его ТЗ и равен J z / W =– n . Таким образом, вихревой пучок с ТЗ и ОУМ, равным – n , можно сформировать с помощью краевой дислокации n -го порядка и двух цилиндрических линз.

3.    Моделирование

На рис. 1 показаны распределения интенсивности и фазы в начальной плоскости, и на двойном фокус- ном расстоянии цилиндрической линзы Гауссова пучка с линией нулевой интенсивности n-порядка (уравнения (1), (2)).

б)

в)

г)

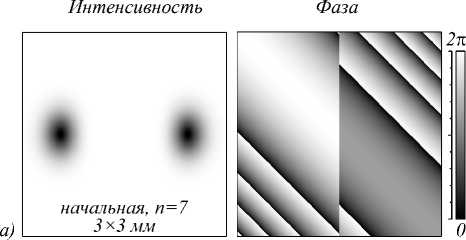
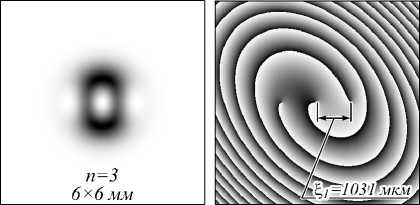
Рис. 1. Распределения интенсивности (первый столбец, негатив) и фазы (второй столбец) в начальной плоскости

Гауссова пучка с краевой дислокацией при n = 7 (первая строка, а) и на двойном фокусном расстоянии цилиндрической линзы при порядке n = 3 (вторая строка, б), n = 7 (третья строка, в), n = 10 (четвёртая строка, г)

Распределения в начальной плоскости были получены по формуле (1), а на двойном фокусном расстоянии – по формуле (2). Параметры расчёта: длина волны λ =532 нм, радиус перетяжки Гауссова пучка w =0,5 мм, фокусное расстояние цилиндрической линзы f = 1 м, расчётная область во входной плоскости | x |, | y | ≤ 1,5 мм, расчётная область в выходной плоскости | ξ |, | η | ≤ 3 мм для n =3 и 7, и | ξ |, | η | ≤ 4 мм для n = 10.

Из рис. 1 следует, что действительно вертикально расположенная краевая дислокация порядка n =3, 7, 10, на которой происходит «сбой» фазы, преобразует- ся на двойном фокусном расстоянии цилиндрической линзы в эллиптические оптические вихри (изолированные нули интенсивности) минус первого порядка, расположенные на горизонтальной оси, разделенные расстоянием (3), и их число соответственно равно n = 3, 7, 10. Для n =3 координаты дислокаций ξ можно так же определить по формуле ξ1,2 = ±w(1 +γ2)1/2(γ2/3)-1, результат которой совпадает с их нахождением на рис. 1б: ξ1,2 = ± 1031 мкм.

Заключение

Теоретически показано, что астигматическое преобразование краевой дислокации (прямой линии нулевой интенсивности) n -го порядка формирует на двойном фокусном расстоянии от цилиндрической линзы n оптических эллиптических вихрей (винтовых дислокаций) с топологическим зарядом –1, расположенных на прямой линии, перпендикулярной краевой дислокации, в точках, координаты которых являются корнями многочлена Эрмита n -го порядка. Орбитальный угловой момент краевой дислокации с астигматической фазой пропорционален n .

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант 18-2920003, параграф «Комплексная амплитуда поля с краевой дислокацией на двойном фокусном расстоянии»), Российского научного фонда (грант 18-1900595, параграф «Орбитальный угловой момент»), а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (параграф «Моделирование»).