Преобразование линейной поляризации в круговую при острой фокусировке оптического вихря

Известно, что при острой фокусировке света с круговой поляризацией из-за спин-орбитальной конверсии вблизи фокуса формируется орбитальный поток энергии [1 –7]. Начальный пучок не имеет орбитального углового момента (ОУМ), а имеет только осевую проекцию вектора спинового углового момента из-за наличия круговой поляризации. Но в сильном фокусе из-за появления продольной составляющей вектора напряженности электрического поля формируется поперечный поток энергии, приводящий к ненулевой продольной проекции ОУМ. В работах [8– 12] изучалось поведение спинового углового момента (СУМ) и орбитального углового момента в остром фокусе вихревых пучков. С другой стороны, известны работы по обратному потоку в остром фокусе оптических вихрей [13– 16] и в некоторых лазерных пучках, таких как, например, векторные X-волны [17], непараксиальные пучки Эйри [18], пучки Вебера [19], векторные пучки Бесселя [20] и дробные вихревые пучки Бесселя [21].

В данной работе мы получили с помощью теории Ричардса–Вольфа аналитические выражения для проекций вектора Пойнтинга (потока энергии) и вектора СУМ для случая острой фокусировки оптического вихря с топологическим зарядом 2 и линейной поляризацией. У такого пучка на входе нет составляющих вектора СУМ. Но вблизи фокуса у вектора СУМ все составляющие отличны от нуля. Это объясняется об- ратным эффектом по отношению к эффекту спин-орбитальной конверсии. То есть в данном случае из-за орбитально-спиновой конверсии начальный вихревой пучок c линейной поляризацией формирует в фокусе пучок с круговой поляризацией. Но у вихревого пучка с топологическим зарядом m =2 имеется особенность. Такой вихревой пучок формирует на оптической оси в фокусе обратный поток энергии (продольная проекция вектора Пойнтинга отрицательная). И при этом на оптической оси имеется ненулевая интенсивность. При любом другом m >2, кроме m = 1 и m =2, на оптической оси будет нулевая интенсивность и нулевой поток энергии.

Заметим, что для спин-орбитального взаимодействия (связи) нужна среда, и поэтому везде в данной работе используется спин-орбитальная конверсия (преобразование). Из-за схождения лучей в фокус появляется продольная проекция вектора напряженности электрического поля, которая вместе с поперечными составляющими формируют поперечный поток энергии (начальный поток энергии имел только продольную составляющую), который, в свою очередь, формирует продольную составляющую вектора ОУМ. Две поперечные проекции вектора напряженности электрического поля в фокусе имеют относительную задержку по фазе на π /2 и формируют круговую поляризацию, которая, в свою очередь, формирует продольную компоненту вектора СУМ.

Поток энергии и СУМ в фокусе

В [6] получены выражения для проекций векторов напряженности электрического и магнитного полей вблизи острого фокуса для оптического вихря с любым целым топологическим зарядом m и начальной линейной поляризацией. При этом обратный поток энергии вблизи оптической оси в фокусе формируется при любом m ≥ 2. Но только при m =2 максимальное значение обратного потока формируется на оптической оси. Поэтому рассмотрим фокусировку оптического вихря с топологическим зарядом m =2 с линейной поляризацией. С помощью теории Ричардса– Вольфа [14] можно найти проекции вектора напряженности электрического поля в остром фокусе апла-натической системы. Для нашего начального светового поля

E = A ( 9 ) e i² Г I , H = A ( 9 ) e ^{i 2}» I 0 I ,

I 0 )                         I 1 )

где E и Н – вектора напряженности электрического и магнитного поля, в плоскости фокуса проекции вектора напряженности электрического поля будут иметь вид [22]:

E x = ie I 1 0 2 + ' e1 2,4 + -2 e1 2,0

I , V2       , V2

,

E„ =-e2      ' e212 4+ ' e2b 0|,(2)

( V2        V2

E z = 2 e ² I     e i » 1 13 —U e ^-Ф 1 1

IV2 ’V 2

где

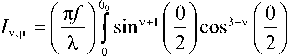
X cos ¹/² ( 9 ) A ( 9 ) e k cos ⁹ J _ц ( x ) d 9 ,

где λ – длина волны света, f – фокусное расстояние апланатической системы , x = kr sinθ, J μ ( x ) – функция Бесселя первого рода и NA = sinθ 0 – числовая апертура. Начальная функция амплитуды A (θ) (предположим, что это действительная функция) может быть константой (плоская волна) или в виде Гауссова пучка

A ( 9 ) = exp

Г-у ² sin ² 91 ( sin ² 9 ₀ )

Найдем проекции вектора спинового углового момента (СУМ)

S = 2 Im [ E * x E ] ,

где Im – мнимая часть числа, E * – комплексное сопряжение вектора напряженности поля. Подставляя

• (2) в (5), найдем выражения для проекций вектора СУМ в плоскости фокуса ( z = 0) для оптического вихря ( m = 2) c начальной линейной поляризацией (1):

S x = ( 1 1,1 1 2,0 - 1 1,3 1 2,4 ) sin Ф + ( 1 1,1 1 2,4 - 1 1,3 1 2,0 ) sin3 » ,

S y = ^- ( 1 1,1 1 2,0 ^- 1 1,3 I 2,4 ) ^{cos ф -}

• ^- ( 1 1,1 1 2,4 ^- 1 1,3 I 2,0 ) ^{cos 3 ф -                               (6)}

• ^- V² 1 2,0 ( 1 1,1 ^- 1 1,3 ) ^cos Ф ,

  S z = 2 ( 1 2,0

  
  

  I 2,4 ) ^x ( I 2,0

  
  

  + I 2,4

  
  

  + V2 1 0,2

  
  
  

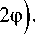
Из (6) видно, что на оптической оси ( r =0) продольная проекция СУМ будет отлична от нуля и положительная:

S z ( r = z = 0) = 2 1 22,0 .                                 (7)

Это означает, что в фокусе в близи оптической оси имеет место правая круговая поляризация. Из последнего уравнения в (6) также видно, что в плоскости фокуса поляризация будет неоднородная. Например, на радиусах, для которых выполняется равенство I 2,0 = I 2,4 , поляризация будет линейная, так как S z =0. А в тех областях фокальной плоскости, где S z <0, будет левая круговая поляризация. Вдоль лучей, выходящих из центра в плоскости фокуса под углами φ: π /4, 3π /4, 5π /4 и 7π /4, поляризация будет чередоваться: при 1 2,₀ >  1 2,4 — правая круговая, при 1 ₂²,₀ = 1 2,₄ - линейная и при 1 2,₀ <  1 2,4 - левая круговая. Из первых двух уравнений (6) видно, что при φ = π n , n = 1, 2,… S x =0, а при φ = π / 2+π n , n = 1, 2,… S y =0. Это означает, что в продольных плоскостях yz и xz вблизи фокуса также имеет место круговая (или эллиптическая) поляризация.

Приведем далее выражения для проекций вектора Пойнтинга (потока энергии)

• P = 2 Re [ E * x H ]

в плоскости фокуса для случая фокусировки оптического вихря ( m =2) с линейной начальной поляризацией:

P x =- Q ( r )sin Ф ,

P y = Q ( r )cos Ф ,

P z = 2 ( 1 02,2 - 1 22,4 - 1 22,0 ) ,                                ⁽⁸⁾

Q ⁽ r ) = 2 [ 1 1,3 ( I 0,2 + I 2,4 ) + 1 1,1 ( I 0,2 + I 2,0 ) ] .

Из сравнения (6) и (8) видно, что распределение вектора СУМ по плоскости фокуса не обладает радиальной симметрией из-за начальной линейной поляризации света, а распределение продольной проекции потока энергии в плоскости фокуса обладает круговой симметрией. Заметим, что распределение интен- сивности в плоскости фокуса также, как и СУМ, не обладает радиальной симметрией:

I = \EX p + \Ey p + \EZ p =

= 1 22,0 + 1 02,2 + 1 22,4 + 2 1 121 + 2 11,3 -                          (9)

-211,111,3 cos ф + V210,2 (12,0 + 12,4 ) COs2ф и на оптической оси интенсивность отлична от нуля (I(r = 0) = 12,0). Из (8) следует, что на оптической оси поток энергии равен по величине продольной проекции СУМ (7), но имеет противоположенный знак:

P z ( r = z = 0) = - S z ( r = z = 0) = - 2 1 22,0 . (10)

То есть поток энергии на оптической оси в фокусе отрицательный (направлен против распространения начального пучка света). Также из (8) следует, что поперечный поток энергии вращается вокруг оптической оси против часовой стрелки:

P r = 0, P , = Q ( r ). (11)

На самой оптической оси поперечный поток энергии равен нулю ( P ф ( r = 0) = Q (0) = 0). Получается, что в плоскости фокуса вблизи центра (вблизи оптической оси) и поперечный поток энергии, и вектор поляризации вращаются против часовой стрелки. Но отличие в том, что поперечный поток энергии (11) на самой оси равен нулю, а продольная составляющая СУМ (7) на оси имеет максимальное положительное значение. Если поместить в фокус поглощающий микрошарик с центром на оптической оси, то продольная проекция СУМ должна вращать этот шарик вокруг оптической оси против часовой стрелки [22].

Далее покажем, что если поменять знак у топологического заряда оптического вихря ( m =– 2) с линейной поляризацией, то обратный поток на оптической оси в фокусе сохранится, а продольная компонента СУМ станет отрицательной. Действительно, проекции вектора напряженности электрического поля в фокусе для начального оптического вихря ( m =–2) с линейной поляризацией вместо (2) будут иметь вид:

E x = ie - ^2iф I 1 0,2 + -1= e ^2iф 1 2,4 +      e ^-2iф 1 2,0

(    72        72

E„ = - e ^-2iф I — 1= e ^2iф I _{2 4} + 1= e ^-2iфP ₀

y ( 72,72        ’

E z

= 2 e ^-2iф I -1= eI ■ 3 —U e ^-iф 1 1 I 72 ’72

Используя (12), можно найти продольные компоненты вектора Пойнтинга и вектора СУМ:

P z = 2 ( 1 02,2 - 1 22,4 - 1 22,0 ) ,                              (13)

S z =- 2 ( 1 2,0

-

1 2,0 + 1 2,4 + V2 1 0,2 COS 2 ф ) .

Из сравнения (6), (8) и (12) следует, что при смене знака топологического заряда оптического вихря продольная компонента вектора потока энергии не изменилась, а продольная компонента СУМ только поменяла свой знак. Это означает, что на оптической оси поток энергии обратный, а осевая проекция СУМ отрицательна (левая круговая поляризация):

P z ( r = z = 0) = S z ( r = z = 0) = - 2 1 2,0 . (14)

Таким образом, оптический вихрь с линейной поляризацией в остром фокусе на оптической оси из-за эффекта орбитально-спиновой конверсии формирует обратный поток энергии и правую ( m = 2) или левую ( m = – 2) круговую поляризацию. При этом вектор поляризации на оптической оси вращается в ту же сторону, что и поперечный поток энергии: против часовой ( m = 2) стрелки и по часовой ( m = – 2) стрелке.

Описанные выше рассуждения можно кратко подытожить следующим образом. В начальной плоскости имеется оптический вихрь с линейной поляризацией. У такого пучка есть только продольная компонента ОУМ (так как в начальной плоскости у вектора электрического поля только поперечные проекции (1)), а все проекции вектора СУМ равны нулю. Известно, что вектор углового момента равен сумме векторов ОУМ и СУМ и сохраняется при распространении пучка в свободном пространстве [4, 5, 10]. Поэтому в фокусе из-за того, что появились отличные от нуля все проекции вектора СУM, должны появиться и все проекции у вектора ОУМ.

Моделирование

Моделирование было проведено при следующих условиях: длина волны λ = 633 нм, падающее поле ограничено апертурой диаметром 8 мкм. Поле представляет собой плоскую волну с единичной амплитудой, линейной поляризацией и фазовым вихрем m = 2 (рис. 1), умноженное на сферическую волну, сходящуюся на расстоянии f = 1,31 мкм (числовая апертура NA = 0,95):

E_x = exp ( i ( kf - m ф-ю t ) ) , E_y = 0.

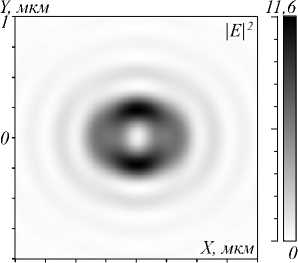
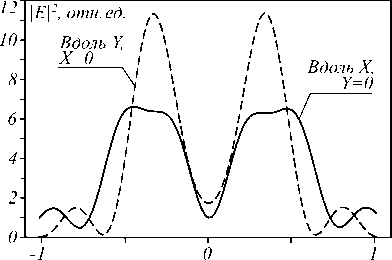
При таком начальном поле в фокусной плоскости наблюдается распределение интенсивности, изображенное на рис. 2. Моделирование проводилось методом FDTD с помощью программного пакета FullWave. Сетка отсчетов была взята λ /30 по всем трем осям, само начальное поле содержало 601×601 отсчетов. Нечетное число отсчетов взято для симметрии поля относительно центра координат.

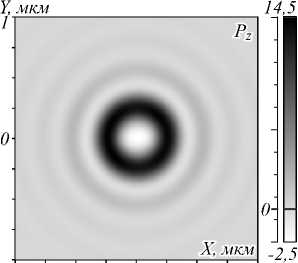
Из рис. 2 видно, что в фокусе волны с линейной поляризацией наблюдается область размером 0,3 мкм вдоль оси X и 0,27 мкм вдоль оси Y, в которой проекция вектора Пойнтинга на оптическую ось отрицательна.

Рис. 1. Фазовый вихрь m = 2 в падающем поле (а) и

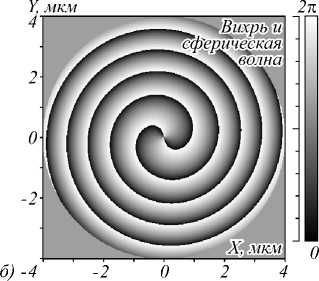
итоговая фаза начального поля со сферической волной (б)

а) -1                 0               1

б)                                         X, Y, мкм

в) -1                 0               1

г)

Распределение поляризации Обозначение эллипсов Y мкм 0,50 0,25 О -0,25 -0,50 -0.75.......

д)    '-0,75 -0,50 -0,25 0 0,25 X, мкм

Рис. 2. Интенсивность (негатив) (а), проекция вектора Пойнтинга на оптическую ось Z (в) в фокусе сферической волны с линейной поляризацией и фазовым вихрем m = 2, их сечения вдоль осей X, Y соответственно (б, г), а также распределение поляризации (д) в фокусной плоскости f = 1,31 мкм. Эллипсоидами обозначено вращение вектора поля E в точках, находящихся в центрах этих эллипсов, жирная точка на конце эллипсоида обозначает начало вращения в одном периоде. Сторона расположения жирной точки на эллипсоидах находится в соответствии с фазой поля.

Ось Z направлена на читателя

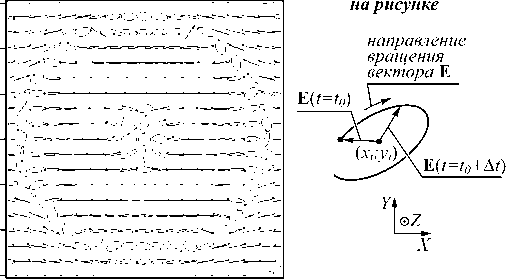
Также видно (рис. 2 д ), что в этой области наблюдается постепенный переход от линейной поляризации к круговой на оптической оси, при этом электрический вектор на оси и близ неё вращается против часовой стрелки. По краям этой центральной области находятся две другие области, в которых вектор E вращается по часовой стрелке (X=0, –0,2E вращается по часовой стрелке (X>0, Y=0), как видно из рис. 2д.

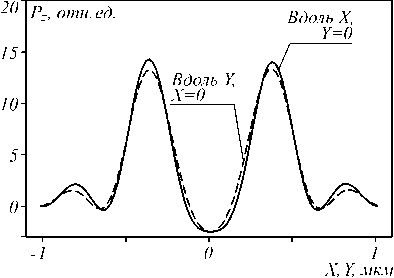
На рис. 3 показаны рассчитанные по формуле (5) двумерное распределение проекции вектора СУМ Sz и их сечения вдоль осей X и Y через оптическую ось. Видно, что проекция вектора СУМ на ось Z на оптической оси отлична от нуля и положительна в границах (0,267

а)   -0,75 -0.50 -0,25 0 0,25 X, мк.м

б)

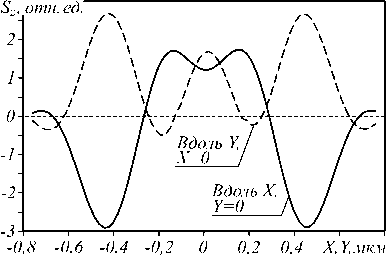
Рис. 3. Проекция S z вектора спинового углового момента на ось Z (а) и её сечения вдоль осей X и Y (б)

Если в поле, изображенное на рис. 2, поместить поглощающую наночастицу, то она будет испытывать момент силы, вращающий её вокруг собственного центра массы из-за наличия круговой поляризации. На рис. 4 показан результат расчета проекции момента силы M z , действующей на частицу диаметром 0,3 мкм и показателем преломления n =1,5 + 0,3 i вокруг оси Z , совпадающей с оптической осью. Мощность всего падающего пучка была принята 100 мВт. Расчет проводился при той же сетке отсчетов λ /30 по всему полю, но в районе частицы (в границах –1,5

Из рис. 4 видно, что в центре пучка ( X =0) момент силы максимален и вращает частицу против часовой стрелки в соответствии с направлением поляризации на оптической оси. Далее, при смещении частицы в положительную сторону оси X момент падает, меняет знак и приблизительно в точке X =0,6 мкм (область кольца с отрицательным Sz на рис. 2 в , г ) момент силы становится максимальным по модулю и направлен по часовой стрелке. Из рис. 2 д мы видим, что в данной области поляризация вновь приобретает эллиптичность и вектор E вращается по часовой стрелке, что соответствует направлению проекции момента M z .

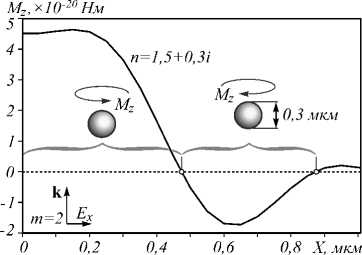
Рис. 4. Проекция момента силы Mz, действующая на частицу при смещении её из центра (X = Y = 0, Z = f) вдоль оси X. Показатель преломления частицы n = 1,5+0,3i, мощность пучка равна 100 мВт

Заключение

В работе на основе теории Ричардса–Вольфа получены аналитические выражения для проекций вектора Пойнтинга и вектора спинового углового момента вблизи фокуса для случая острой фокусировки оптического вихря с топологическим зарядом +2 и – 2 и линейной поляризацией. Из полученных соотношений следует, что в плоскости фокуса вблизи оптической оси имеет место обратный поток энергии. В области обратного потока энергии формируется правая ( m =2) или левая ( m =–2) круговая поляризация. В периферийной части плоскости фокуса поляризация неоднородная: имеет место чередование правой круговой (или эллиптической) поляризации на левую круговую (или эллиптическую) поляризацию и на линейную поляризацию. Но вблизи оптической оси направление вращения вектора поляризации совпадает с направлением вращения вокруг оптической оси поперечного потока энергии: поток энергии и вектор поляризации вращаются против часовой стрелки при m =2 и по часовой стрелке при m =–2. Формирование круговой поляризации в области обратного потока энергии позволяет обнаруживать его. Действительно, если поместить вблизи фокуса в область обратного потока поглощающую наночастицу, то она из-за спинового углового момента будет вращаться вокруг центра масс. Поперечный поток энергии равен нулю на оптической оси, поэтому он почти не будет участвовать во вращении частицы. Направление вращения частицы будет определяться знаком топологического заряда вихревого пучка.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант 18-29-20003) в части «Поток энергии и СУМ в фокусе», Российского научного фонда (грант 18-19-00595) в части «Моделирование», а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в частях «Введение» и «Заключение».