Преобразование решения Надаи в решение Прандтля для системы двумерной идеальной пластичности

Рассмотрим хорошо известную систему теории плоской идеальной пластичности с условием текучести Сен-Венана-Мизеса, записанную для функций у (х, у), и(х,у) в декартовой системе координат [1]:

5ст      f 59          59 .)

дх    (5х        су)

5ст     Г59        59)

-—2^ — sin29- — cos29 =0, су     (дх        ду)

где ст(х,у) -гидростатическим давление, 9(х,у) + л/4 -угол между главным направлением тензора напряжений и осью Ох.

Система (1) является гиперболического типа, два семейства характеристик задаются следующими уравнениями:

^ = tg9, ^ = -ctg9.          (2)

dx        dx

Как известно [1], система (1) линеаризуется преобразованием годографа х = х(ст,9), у = у>(ст,9)

в области, где якобиан соответствующего преобразования отличен от нуля. Линеаризованная система имеет вид

Эх     (Эх        Эи

— -2^ —cos 29+-^-sin 29

59      (5ст          5ст )

ду     (дх . ду

-^--2^ — sin 29cos 29

59      (5ст 5ст )

= 0,

= 0.

Ввиду линеаризуемости, система (1) допускает бесконечномерную группу точечных симметрий [2] с оператором

5          д

25 = х0(ст,9)—+ у0(ст,9) —,           (4)

дх         ду где (x0,_y0) является произвольным решением системы (3). Соответствующие точечные преобразования, переводящие любое точное решение системы (1) в решение этой же системы имеют вид х'= х + ах0(ст,9), у' = у + ау0(а,9),      (5)

где а - достаточно малый вещественный групповой параметр.

Рассмотрим два точных решения линейной системы (3): Xi = (х1(ст,9),у1(ст,9)),

%2 = ((ст, 6), У2 (ст, 9))              ^

и возьмем в качестве функций (х ,j^) разности х0=Х]-х2, у’о=Л’1->’2-           (7)

Тогда в силу (5) будем иметь так называемое размноженное решение х = х'(ст, 9) = х2 (ст, 9) + ах0 (ст, 9) =

= о^(ст,9) + (1-а)х2(ст,9),

У = уХ<У 9) = у₂ (ст, 9) + ау₀ (ст, 9) = = аУ1 (о, 9) + (1 - а)у₂ (ст, 9), которое в силу линейности системы (3) задает ее решение как линейную комбинацию точных решений. Но (8) задает неявным образом решение и для системы (1). Этот принцип можно назвать принципом суперпозиции для системы плоской пластичности (1). На основе этого принципа любое точное решение системы (1) можно связать с другим точным решением.

Получаемые таким образом решения требуют, конечно, механической интерпретации, т. е. определения конкретной граничной задачи. Отметим, что соотношения (8) задают семейство решений, зависящее от параметра а.

Рассмотрим известное решение Надаи для сходящегося канала, имеющее вид [3]:

соотношения г cos2w ,   , c-cos2w ср = ------!—цщ, ср =---------

•с - cos 2щ          cos 2щ

(Ю)

Здесь постоянная с связана с углом раствора канала 26 следующим образом:

а + у = С arctg

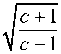
(И)

а е 0,- , а £ является постоянной пластичности. Интегрируя (10), получаем неявную зависимость между полярным углом ср и углом щ:

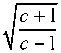
Условие на константу с необходимо для сходимости интеграла (10), константаА произвольная. Данное решение описывает напряженное состояние в клиновидной области, в котором границы клина являются огибающими линий скольжения.

Запишем решение (9)- (12) в терминах функций ст и 0 системы (1), пользуясь формулами связи компонент девиатора напряжений в полярной и декартовой системах координат [4]:

s_r = ^-5_Ф = -^51н20со5 2ф +

+^cos20sin2cp = ^sin2(cp-0),(13)

тГф = ^со$2(ф-0).

Таким образом, в декартовой системе координат решение (9) для системы (1) имеет вид ог +с> ст =------- =

= -£с[1п(х2 + у1) + 1и(с - cos2ф)] + А,(14)

0 = cp--arccos-^ = ф + ф ——.

Из (12) находится выражение для ср + ф, и с учетом второго соотношения из (14) будем иметь:

<15>

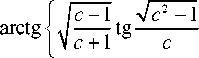
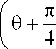
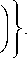
Кроме того, имеем cos 2щ = cos 20 - 2ф + ^ j = зт(2ф - 20), и тогда решение Надаи для сходящегося канала в терминах у и и принимает вид ст = -kc\ 1п(х2 + у2) + In\с + sinI 29-2arctg— В + Л,

9 = arctg — - — + arctg х 4

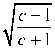
(|б)

с (     4 J Г

Граничные условия для решения (16) следующие. Канал образован прямыми ф = ±а, вдоль которых (берем только верхнюю прямую L : ф = а)

тогда

71               7

Т = 4, т_Гф = к,

⁶L = ^а> ст|_£ = -Лс1п(х² + у²)+А.

Теперь запишем решение Надаи для линеаризованной системы пластичности, те. выразим х и у из(16):

x_N = ±е ^2fc / ^(0), y_N = +x_NT,

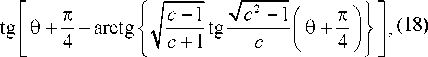
5(0) = Vc+сГ2 +(l-r2)sm20-2rcos20,

Здесь индекс N указывает, что это решение A. Nadal. Теперь достаточно просто построить линии скольжения, полагая в (18)

ст = 2^-0), ст = 2£(С2+0) (19) и беря и в качестве параметра (рис. 1). При этом параметр и принимает значения от -а - л/2 до а.

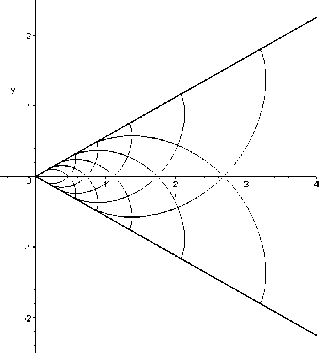
Рис. 1. Линии скольжения решения Надаи для сходящегося канала

Рассмотрим решение Прандтля ст = -^-^_ + ^1-^ (20)

у = И cos 20, описывающее сжатие тонкого слоя параллельными плоскими шероховатыми плитами. Здесь 2/z = const является шириной слоя, -р = const является значением гидростатического давление при х = 0. Граничные условия выражаются формулами (берем только верхнюю границу у = /г)

0| . = 0, ст| ь

\у=П ’ \y=h               и

Соответствующее решение линеаризованной системы (3) имеет вид (индекс Р)

Хр = -СТ--Д--/751н20, к к                    (2t)

у_Р = h cos 20.

Уравнения линий скольжения получаются из (21) заменой (19). Для решения Прандтля соответствующие характеристики изображены на рис. 2.

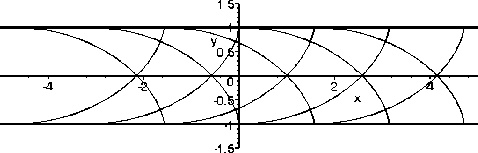
Рис. 2. Линии скольжения решения Прандтля для сжимаемого слоя

Размноженное решение (8), получаемое из принципа суперпозиции решений (18) и (21) имеет вид х = ах„ + (1 - а)х„,

" Р                (22)

У = ^аУх - О - ^а)Ур-

Для построения огибающих линий скольжения для размноженного решения (22) производим замену (19) и используем необходимое условие существования огибающей семейства кривых х = хф,С,\ у = уф,С,\ выражаемое равенством

5С, 59 5С, 50 °’ 1 1,2т которое в силу (2) дает два уравнения для значений Сх первого и С2 второго семейств характеристик:

7^-^ctg9 = 0, оС_х оС_х

Решая (23), получим

С] =-9+2$-_с1и

С2 = 9+ — -cln

2      2^

— + — tgO = 0. 5С2 5С2

I - л S*(9) а 1-Г ctg9 / 1-а SX9)

а 1 + Г tg9 /

уравнений (3), а значит, задает в неявной форме точное решение исходной системы (1); описывает напряженное состояние слоя с границами (25), (26) (рис. 3) и имеет следующие граничные условия заданные параметрически:

I л               1-а ^(0) )

ст г = Л-2Лс1и -1Нс,

^1г‘           ( a 1-Tctg9/

^^(О), У = УсА^’ 9е(о,а);

I                    1-а ^(0) )

ст L = Л-2Лс1и -2hc,

|Г2            ( a 1 + Ttg6)

x = x_cf6), у = у_С1ф), 9_е^Л-_а,-^.

При а = 0 решение (22) совпадает с решением Пранд-ля, при а = 1 - с решением Падай.

a * 0,1.

Подставляя (24) в уравнения характеристик, получим уравнения огибающих:

х^ = -(1 - a^h х

х sin29-2cln

I - л S*(9) a 1-Tctg9

Г, :

2(1 - a)hc (1 - a)h ,       ,

~1-Tctg9 k + A yCi = (1 - a)h cos 29 -

Kf-aVic

—;—t 06(°,a)

I 1-TctgO v '

х_с = -(1 - a)h х

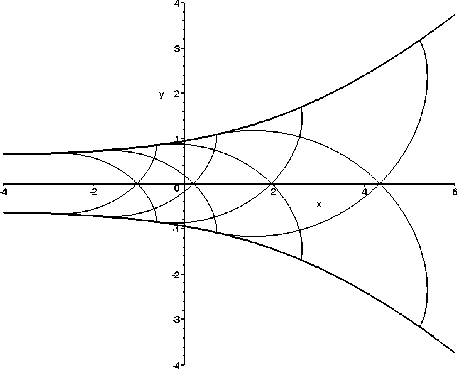
Рис. 3. Линии скольжения размноженного решения

х sin29-2cln

I - л SX9) a 1 + Ttg9

Г2 :

2(1 - a)hc (1 - a)h _{z ч}

” 1 + Ttg9 k + P1’’ yc = (1 - a)h cos 29 - 2(1 ~ T,

• ¹                 1 + Ttg9

• ^{6    6} [     2’~2

  
  

Можно заметить, что огибающая Г переходит в огибающую Г2 при замене 9 на - л/2 - 9.

Таким образом, размноженное решение (22) при а ^ О, 1 является новым точным решением в замкнутой форме