Преобразование схем дорожных сетей

При построении дорожных схем нередко используются два. основных элемента. — бинарный разделитель и бинарный сумматор. Схемы только из данных элементов легко представляются в виде геометрических графов, элементы, получаемые при пересечении ребер (узлы), мы рассматривать в данной работе не будем, считая, что по теореме Понтрягина-Куратовского во всех представленных случаях они могут быть удалены выходом из плоскости.

В процессе упрощения будем не только исключать у графов геометрическую привязку, но и возвращаться к ней, потому что, какой бы схемой мы не заменили дорожную сеть, в конечном счете она. должна, соответствовать реальной картине и иметь возможность применения на. практике.

В качестве основного преобразования будем разделять и объединять графы на. подграфы, где только один вход и все выходы, которые он соединяет. Тем самым мы будем получать подсхемы числом, равным числу входов в систему. Также сохраним в данных схемах направленность движения по ребрам (от входа к выходам). Будем называть такие подсхемы «разделитель-объединитель» схемами или Р-О-схемами.

Все Р-О-схемы довольно просты, поэтому их легко можно упростить путем устранения лишних элементов; установив, где имеются лишние элементы, станет легко упростить и нашу начальную схему. Но, так как при удалении вершины из графа, уходят все ребра, соединенные с этой вершиной, данный метод не подходит для упрощения схем, поэтому в настоящей работе рассмотрим несколько других методов, с помощью которых мы сможем упрощать дорожные схемы, и приведем пример алгоритма, следуя которому, мы сможем это сделать.

1.    Разделение и объединение схем

Наиболее нетривиальным шагом в процессе преобразования дорожных сетей является переход от единого графа, дорожной сети к множеству Р-О-схем. Остановимся на. данном моменте чуть подробнее.

Рассмотрим переход от единого графа, к множеству подсхем на. примере небольшого перекрестка, изображенного на. рис. 1.

Данный граф имеет два входа (А и В), следовательно, он разбивается на две подсхемы. Наиболее простой способ разбиения графа. - это преобразование начального графа, путем поэтапного удаления всех вершин-входов, кроме одной, относительно которой строится подсхема, затем обнуления участков, принадлежащих удаленным входам, то есть имеющим обратную относительно входа направленность. Таким образом, мы получаем первую подсхему. Затем повторяем процедуру для другого входа. Результат разбиения графа, изображенного на рисунке 1, показан на рис. 2.

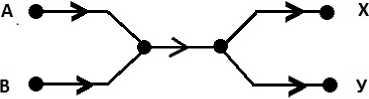
Рис. 1

Рис. 2

Представим процесс обратного перехода от двух подсхем, показанных на рис. 2, к схеме на рисунке 1. Для этого на каждой из подсхем выбираем количество точек, лежащих на ребрах данной подсхемы, равное максимальному числу выходов среди всех подсхем; при этом выбранные точки должны лежать на разных маршрутах подсхемы, соединяющих вход с выходом. (В случае, если число выходов в подсхемах неодинаково, тогда не все выбранные точки будут задействованы). После этого совмещаем подсхемы в выбранных точках. У получившегося графа появляются ребра кратностью больше одного, для этих ребер уменьшаем кратность до единицы, как показано на рис. 3.

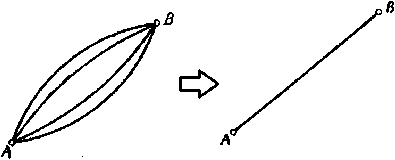
Рис. 3

Примеры того, каким образом можно соединить подсхемы на рис. 2, смотрите на рис. 4. При указанном совмещении у нас появляются не просто ребра кратностью больше единицы, но и дублируются целые участки сети. В тех случаях, когда участки совпадают (центральный случай на рисунке ниже), их следует полностью совместить. Но когда полного совпадения нет, как, например, на последней схеме, появится необходимость совместить ребро с несколькими ребрами и вершиной их соединяющих. В этом случае алгоритм работы не меняется, но важно помнить, что с одним ребром можно соединить строго определенное число ребер и вершин. То есть с одним ребром можно соединить одно ребро, два ребра и вершину, три ребра и две вершины и так далее.

Заметим, что получившееся таким преобразованием множество графов имеет одинаковую связанность.

2.    Методы упрощения Р—О-схем

Зачастую начальные схемы требуют не столько преобразования, сколько упрощения. Метод разделения и объединения позволяет это сделать очень простым способом. Представив начальную схему в виде Р-О-схем, несложно заметить некоторые моменты, в которых схема может быть упрощена. Тем самым мы будем работать не с основной схемой, а с ее подсхемами и, упростив отдельные подсхемы, при объединении получим уже упрощенные сети.

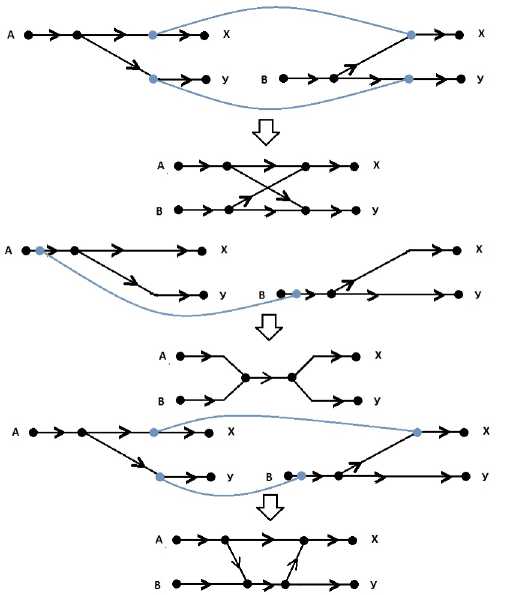
Рис. 4

Для упрощения схем будет использоваться способ уменьшения числа элементов, ребер и вершин графов, который отличается от общепринятого. Когда мы работаем с графом и удаляем, например, одну его вершину, то вместе с ней мы должны удалить и все ее ребра. Данный способ нам не подходит, поэтому введем несколько преобразований, которые пригодятся в упрощении Р-О-схем.

• 1.    Преобразование - Повторение

• 2.    Преобразование - Упрощение

• 3.    Преобразование - Сокращение

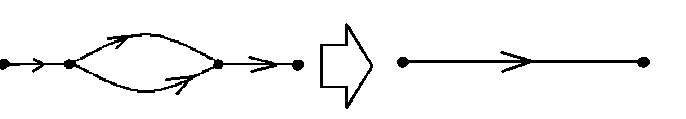
Рис. 5

«Если в подсхеме имеются ребра кратностью больше единицы, то кратность данных ребер необходимо свести к единице». Участок, показанный на рис. 5, - повторение. На нем видно, что центральное ребро имеет кратность два. В том случае, если такой участок встречается в нашем графе, следует заменить кратность центрального ребра на единицу.

«Каждый сумматор в Р-О-схеме может обнулить один делитель в том случае, если данное обнуление сохраняет маршрутизацию схемы». В схеме или участке схемы из нескольких разделений с одним объединением объединение и разделение можно обнулить, но только если в схеме сохранится маршрутизация, то есть вход будет по-прежнему соединен с теми же выходами. На рис. 6 показан пример такого обнуления, в схеме слева имеется более одного маршрута, в данном случае упрощение уберет лишний маршрут.

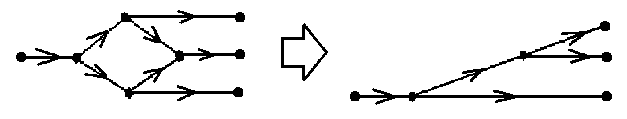
Рис. 6

«Если одна вершина в Р-О-схеме соединена с другой более чем одним способом, то число таких способов следует свести к одному». Пример такого преобразования — схема на рис. 7 с равным числом входов и выходов и равным числом разделений и объединений может быть упрощена исключением лишних пар «объединение-разделение».

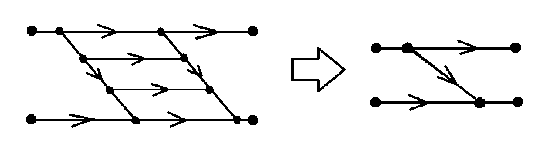
Рис. 7

3.    Алгоритм упрощения Р—О-схем

Используя приведенные свойства, мы можем упрощать любые дорожные схемы, для этого предлагается следующий алгоритм:

• 1)    Дорожную сеть необходимо сначала представить в виде геометрического графа, затем разбить на подсхемы — Р-О-схемы.

• 2)    Далее упрощаем каждую схему отдельно, используя методы преобразования, описанные выше.

• 3)    После упрощения собираем схемы обратно в одну большую. Важно сохранять бинарность отношений, количество входов и выходов, а также число связей между входами и выходами.

4.    Свойства алгоритма упрощения 5.    О работе алгоритма 6.    О множествах, полученных после обработки алгоритмом

Легко заметить, что при использовании описанного алгоритма дорожная схема переходит в некую простейшую схему или множество простейших схем. Рассмотрим несколько важных свойств описанного алгоритма.

Пусть А - произвольная дорожная система. Система А после обработки алгоритмом образует множество дорожных систем {В}, и любая система В1 из множества {В} после обработки алгоритмом также образует множество систем {В}.

Пусть множество дорожных систем {А} имеет одинаковую связанность, тогда любая система А из {А} после обработки алгоритмом образует одно и то же множество {В}.

Таким образом, для того чтобы успешно применять на практике описанный выше алгоритм с учетом указанных свойств, нужно учитывать еще и различные типы условий, при которых мы не можем убирать все лишние элементы из сети, в противном случае мы всегда будем приходить к множеству простейших систем, которое не всегда подходит для практических задач. Рассмотрим различные типы условий:

• 1)    Геометрические (невозможность построить эстакаду, снести дом и т.д.).

• 2)    Аналитические (необходимость разведения потоков).

• 3)    Практические (стоимость, сложность).

7.    Работа алгоритма на практике

Рассмотрим применение алгоритма на еще одном примере - перекрёстке «клеверный лист».

Один из таких перекрестов показан на скриншоте с Яндекс карт, рис. 8.

Рис. 8

В качестве решения предлагается изменение структуры перекрестка. При этом необходимо учесть следующие ограничения:

• 1)    Геометрические — сохранение внеплоскостной развязки с МКАД.

• 2)    Аналитические — необходимость избежать пересечения потоков с наиболее нагруженных направлений.

В процессе анализа данной схемы был сделан вывод, что для того, чтобы развести потоки загруженности, необходимо отказаться от полной маршрутизации. В случае же ее сохранения и учета геометрических ограничений при объединении подсхем мы снова приходим к тому же перекрестку. Заметим, что данная схема симметрична, и все Р-О-схемы для нее будут выглядеть одинаково. Р-О-схема изображена на рис. 9.

Подсхема после упрощения изображена на рис. 10, но с учетом описанных ранее условий мы сведем ее к еще более простой схеме, она изображена на рис. 11.

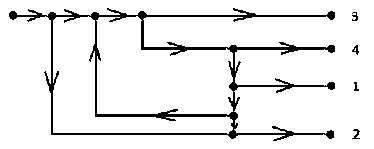
Рис. 9

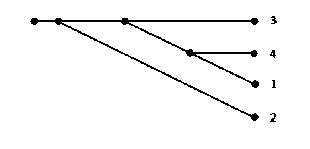
Рис. 10

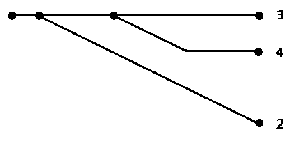
Рис. 11

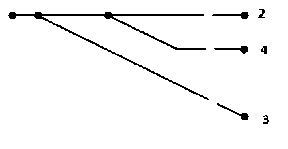
Рис. 12

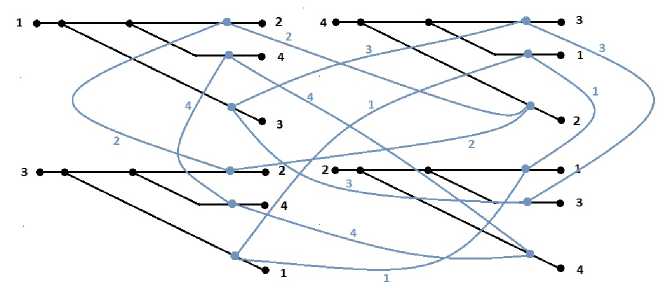
Рис. 13

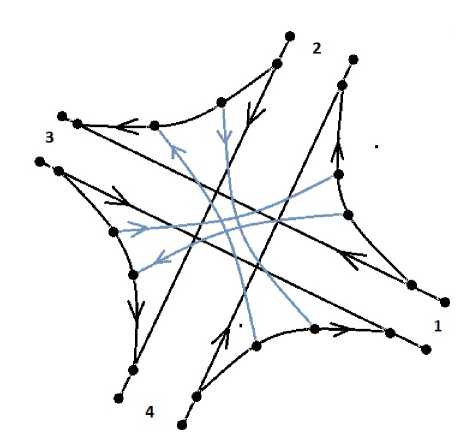
Рис. 14

Рис. 15

С учетом геометрических ограничений способ размещения точек сшивки показан на рис. 12, объединение показано на рис. 13, а на рис. 14 изображен один из окончательных вариантов схемы. Отмечу, что множество схем в данном случае огромно, ниже показан лишь один из вариантов сшивки с учетом наших условий.

Полученная схема развязки двух магистральных дорог хоть и относится к сложным архитектурным решениям (данная развязка четырехуровневая), но она является оптимальной с точки зрения беспробочного разведения двух потоков одинаковой интенсивности, и в мире уже есть примеры построения таких развязок. The Puxi Viaduct, Китай (показана на рис. 15) - одна из наиболее сложных и загруженных транспортных развязок в мире находится в Шанхае. Ежечасно по ней движутся тысячи автомобилей. Пять уровней мостов соединяют две самые загруженные городские магистрали оживленных дорог и беспробочно распределяют транспортные потоки. Подобные примеры есть и в других странах.