Преобразование замедляющихся лазерных пучков в ускоряющиеся

Недавно [1] рассмотрены непараксиальные сохраняющие свою форму ускоряющиеся пучки Вебера, которые распространяются вдоль параболической траектории. Эти пучки Вебера похожи на пучки «половины Бесселя» [2], но в отличие от последних описываются аналитическим выражением. Пучки Вебера–Эрмита также известны как решения параксиального уравнения распространения [3]. В [4] рассматривается общая теория 3D непараксиальных ускоряющихся пучков на основе известных решений уравнения Гельмгольца в параболических, вытянутых и сплюснутых сфероидальных координатах. Эти пучки распространяются по дуге окружности. В [5] предложены пучки Эйри, распространяющиеся с неоднородным ускорением по гиперболической траектории. Хотя эти пучки не сохраняют свою форму (расходятся при распространении), они могут иметь более изогнутую траекторию на конечном её участке, чем обычные пучки Эйри [6].

В этой работе рассмотрен другой подход к формированию ускоряющихся пучков. Он заключается в следующем. Известны параксиальные 2D световые поля, у которых аргумент функции комплексной амплитуды зависит от переменных, как x2 / z, где x – поперечная координата, а z – продольная координата. Это, например, световое поле, которое формируется при дифракции плоской волны на угловой фазовой ступеньке [7]. Или хорошо известное решение задачи дифракции на краю непрозрачного экрана [8]. В этой работе мы рассмотрим и другие решения параксиального уравнения распространения. Световые поля, комплексная амплитуда которых имеет аргумент вида x2 / z, распространяются по траектории корневой параболы x = z1/2. Такие пучки являются замедляющимися, так как «ускорение» (вторая производная вдоль траектории) x'' = -z3/2 имеет противоположный знак со скоростью (первой производной вдоль траектории) x' = z-1/2. Если же амплитуду такого светового поля на расстоянии z0 заменить на комплексно сопряжённую и сдвинуть начало оптической оси в точку z0, то световое поле с такой амплитудой будет распространяться с ускорением по траектории x = (z0 - z)1/2. В этой работе приводятся аналитические выражения для комплексных амплитуд таких ускоряющихся пучков. Кроме того, рассмотрены параксиальные пучки «половины Бесселя», которые отличаются от непараксиальных [2].

1. Ускоряющиеся пучки

Пусть для каждого фиксированного пройденного расстояния z координата максимума интенсивности некоторого лазерного пучка имеет вид x _max ( z ) . Чтобы траектория пучка обладала ускорением на некотором участке, необходимо, чтобы первая и вторая производные координаты максимума x _max по пройденному расстоянию z имели один знак [5]:

dxmax )f d2 xmax dz Д dz2

> 0.

Наиболее широко известными ускоряющимися пучками являются пучки Эйри, комплексная амплитуда которых имеет вид [6]:

E ( x , z ) = Ai ( 5 -^2/ 4 ) exp ( is^/ 2 - i ^3/ 12 ) ,       (2)

где (x, z) - декартовы координаты, s = x I x 0, ^ = z I (kx0), k = 2п I % - волновое число, % - длина волны, x0 – произвольный масштабирующий множитель, Ai(x) – функция Эйри [9, раздел 10.4]. Координа- ты максимумов интенсивности таких пучков имеют вид:

x max

2 z ²

x ⁰ y m 4 k ² x 0 ,

где y_m – точка m -го максимума функции [ Ai ( x )]² . Тогда d x max/ d z = V ^{(2 k 2} x 03 ) и ^d 2 x max/ d z ² = V^{(2 k 2} x 0 ). ^То есть условие (1) выполняется для любых расстояний z >  0 , причём ускорение d² x _max I d z ² имеет постоянную величину. Ниже рассмотрим лазерные пучки, также обладающие ускорением, но которое не является постоянным и уменьшается при распространении пучка.

1.1. Пучки Эйри с гиперболической траекторией

В работе [5] рассмотрены пучки Эйри с гиперболической траекторией, которые в начальной плоскости z =0 имеют комплексную амплитуду

E ( x ,0 ) = exp [ i a ( x/x ₀)³ + i p ( x/x ₀) J ,             (4)

где x ₀ - масштабирующий множитель, a a и p - безразмерные параметры. Траектория такого пучка в зоне дифракции Френеля имеет вид:

x max

(P^- y„ Vta) z kx 33

.

kx ₀         12 a z

Используя условие (1), в работе [5] было показано,

что ускорение возникает на участке

z >  Z 1 =

kx ₀ ²

2^3 ^a ( y „ 3/З а—р )

причём только в случае, когда sign ( a ) р < y_m <(3 | a |)^1/3. Ускорение такого пучка спадает пропорционально z ^–3: d² x max /d z ² =^- kx 0/^{(6 a} z ³⁾.

1.2. Пучки Эрмита–Гаусса

Широко известные пучки Эрмита–Гаусса [10], оказывается, также обладают ускорением. Действительно, пусть в начальной плоскости z =0 световое

поле имеет комплексную амплитуду

E ( x , z

Г _x ² ^   r _x A

= ⁰ ) = exp I--2- I H „ I-I ,

V w J   v a J

где ( x , z ) – декартовы координаты, w – радиус перетяжки Гауссова пучка, n и a – порядок и масштаб полинома Эрмита. Тогда, применив преобразование

Френеля, можно показать, что на расстоянии z от начальной плоскости сформируется поле со следующим распределением комплексной амплитуды [11]:

E ( ^x , ^z ^Jvk exp

2 pz

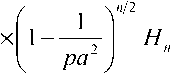
- ikx

² z4 ( pa ) 2 ^- p

^k Г ^k .) 2

--I-- 1 I x

2 z V 2 zp    J

x

где p = 1/ w ² – ik / (2 z ).

Рассмотрим для простоты случай, когда n = 1. Тогда интенсивность пучка (8) в плоскости, находящей-

ся на расстоянии z от начальной, равна:

I ( x , z ) = E ( x , z )| ²

exp - k -Re p x 2

2 a ²1 p|³ z ^{3 P}[ 2 z ²1 p |²    J

Продифференцировав обе части (9) по переменной x , получим необходимое условие для экстремумов

интенсивности:

2 x = ^k - ₂Re p x 3 . (10) z ² p

Случай x =0 соответствует минимуму (так как интенсивность I (0, z ) равна нулю), а координаты максимумов равны

x max =±       -0- ,                               (11)

kz ₀

где z ₀= kw ² /2 – расстояние Рэлея.

Нетрудно показать, что кривая с максимальной интенсивностью является гиперболой. Получим про-

изводные x _max по z первого и второго порядков:

d x max d z

max

V ^kz 0 V ^{z + z} 0

=± 1

2 z ₀

kz ; ( z ²+ z 2 г

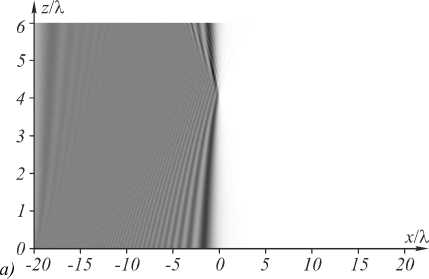
Из (12) видно, что при всех z >0 произведение (d x max /d z ) (d² x max /d z ²) положительно, т.е. пучок Эрмита– Гаусса обладает ускорением, которое, подобно рассмотренным выше пучкам Эйри с гиперболической траекторией, кубически убывает с пройденным расстоянием z . Наличие ускорения у обеих ветвей пучка Эрмита– Гаусса первого порядка может быть заметно при малых расстояниях z . На рис . 1 показана интенсивность такого пучка в плоскости Oxz , рассчитанная методом распространения пучка (BPM). Два локальных максимума пучка Эрмита–Гаусса на рис. 1 распространяются симметрично относительно оптической оси по двум гиперболическим траекториям с ускорением.

z/X

0-                         ■ ■

-20 -15 -10 -5    0    5   10 15 20

Рис. 1. Ускоряющийся пучок Эрмита-Гаусса (X = 532 нм, w = X, a = 2X, n = 1) (негатив)

Заметим, что с ростом номера n у пучка Эрмита–

Гаусса (при a = w /V2) растёт радиус (ширина) пучка

и координата крайних нулей интенсивности (при разных расстояниях z ) описывается оценкой сверху:

I ^x max I ^- 4ⁿ ( ^{n -} 1) * ^{1 +} ^T ,

2                 z ₀

из которой следует, с учётом (12), что величина ускорения пучка Эрмита–Гаусса с ростом номера n растёт линейно при больших n .

Других параксиальных 2D ускоряющихся пучков, которые описываются аналитически, пока не известно . Поэтому в разделе 3 показано, как можно получить ускоряющиеся лазерные пучки из замедляющихся .

2. Замедляющиеся пучки

В отличие от рассмотренных выше ускоряющихся пучков (2), (4), (7), для замедляющихся пучков необ-

ходимо, чтобы первая и вторая производные координаты максимума интенсивности x _max по пройденному расстоянию z были разного знака:

выражение для комплексной амплитуды 2D аналога 3D обобщённой гипергеометрической моды [13]:

I dx max )( ^d 2 x max

V dz JV dz2

< 0.

Е ( x , z ) = z - a 1 F 1 1 a ,-, — I , I 2 2 z J

Рассмотрим примеры таких пучков.

2.1. Дифракция плоской волны на непрозрачном полубесконечном экране

Пусть плоская волна распространяется вдоль оптической оси z и при z =0 проходит через полубесконеч-ную плоскую апертуру, пропускающую свет в области x <0 ( x – координата в плоскости апертуры). Непосредственно за ней комплексная амплитуда будет равна:

1, x <  0,

E ( x , z = 0 ) = ,      ,                              (14)

^V ' |0, x >  0.

После прохождения светом расстояния z его комплексная амплитуда будет определяться преобразованием Френеля от поля (14):

E (x, z) =

где a – произвольная постоянная, ₁ F ₁( a , b , x ) – функция Куммера [9]

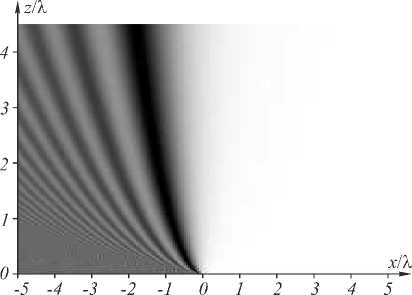
Рис. 2. Интенсивность в плоскости Oxz при дифракции плоской волны на полубесконечной апертуре ( Л = 532 нм; -5 Л Л; 0,1 Л Л ) (негатив)

= 2 {[1 - c (5)-s (5)]+f [ c (5)-s (5)]},       1151

где 5 = V 2/ ( % z ) x , a C ( 5 ) и S ( 5 ) – интегралы Френеля:

C (5) = Jcos II

0 V 2 J 5

S (5) = J sin II

0 V 2 J

Координаты максимумов интенсивности такого

пучка x max равны:

x max

'Rm- -

где 5 m - координата — -го максимума функции 7 ( 5 ) = [1- C ( 5 )- S ( 5 )] ² + [ с ( 5 )- S ( 5 )]². Вычислим первую и вторую производные координаты максимума x max по пройденному расстоянию z :

dx max = 1 Г%5 d z    2 2 z ^m ,

d² x _max d z ²

-     % 5

4 z 2 z ^m

Из (18) видно, что для всех z >  0 выполняется условие (13). Замедление каждого максимума видно на рис. 2, на котором показана интенсивность пучка (15).

2.2. Двумерные гипергеометрические пучки и пучки Бесселя

Подобно тому, как это сделано в [12], будем искать

решение параксиального уравнения распространения

дE д2 E  _

2 ik — + —— = 0, дz   дx

в виде E ( x , z ) = x^p z^q F ( s x^m zⁿ ), где F ( x ) – некоторая функция, s – масштабирующий множитель. Сведя полученное дифференциальное уравнение второго порядка к уравнению Куммера, получим следующее

Известно, что производная любого решения уравнения (19) по любой декартовой координате также является решением уравнения (19). Поэтому можно рассмотреть световой пучок с амплитудой

E ( x , z ) = xz ^a .F a , —, Rx ^V '        ¹¹V 2 2 z

.

В частном случае, при a = 3/4, из (21) следует решение уравнения (19) в виде пучка Бесселя дробного порядка:

E ( x , z ) = —x—J 1 V ^{z + z} 0 4

kx ²

4 ( z + z 0 )

exp

ikx ²

4 ( z + z 0 )

, (22)

где z 0 – произвольная положительная постоянная (чтобы не возникало особенности в плоскости z =0). При получении (22) было использовано тождество 13.6.1 из [9]. Координаты максимумов интенсивности

такого пучка имеют вид:

X„ max

4 (z + z 0 )

y_m , k

где y m – m -й корень уравнения

J14 ( У ) [ J14 ( У ) + 4 J1‘ 4 ( У ) У ] = 0 .

Зависимость (23) подобна зависимости (17), т.е. x _max пропорционально z ^1/2 . Поэтому пучок (22) является замедляющимся, что видно из рис. 3, на котором показана интенсивность такого пучка, рассчитанная BPM-методом ( X = 532 нм, z ₀ = 20 % , область моделирования - 20 % <  x <  20 % , 0 <  z <  80 % ).

3. Преобразование замедляющихся пучков в ускоряющиеся

Из (1) и (13) нетрудно заметить, что простая замена переменных z ^ z ₀- z приводит к смене ускорения на замедление и наоборот. В самом деле, рассмотрим световой пучок, комплексная амплитуда которого по-

лучается из (15) комплексным сопряжением и заменой 5 на 5 = 2/[X ( z 0 - z ) J x :

E ( x , z >  z 0 ) =

E ( x , z <  z 0 ) =

1 JE ¹ - C ( 5 ) - S ( 5 ) J -J

• 1                                           J .

• ²    [- i E C ( 5 ) - S ( 5 ) J J

• 1    J[ 1 - C ( n ) - S ( П ) J+'

,

• ²    [+ i [ C ( n ) - S ( n ) J J

где П = V2/[^X (

^{z - z} 0) J • ^x .

Второе решение, равное

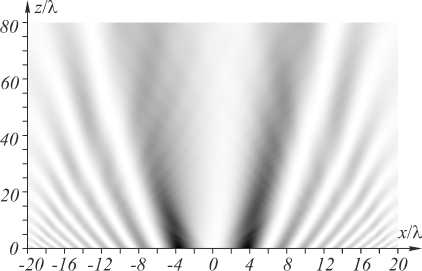
Рис. 3. Интенсивность в плоскости Oxz светового пучка (22)

Световой пучок (24) будем называть пучком Френеля. Используя пределы lim C (x) = —, lim S (x) = —,                    (25)

x ^~         2 x ^~         2

получим, что вблизи плоскости z = z ₀ (вблизи фокальной плоскости), но при z <  z ₀ комплексная амплитуда имеет вид:

z                x    f 0, x >  0,

E ( ^x , z ^ z 0 ^{- 0} ) = 1                             ⁽²⁶⁾

^ 1, x <  0.

Интенсивность светового пучка (24) в плоскости Oxz показана на рис. 4.

Рис. 4. Интенсивность светового пучка (24) в плоскости

Oxz (Длина волны X = 532 нм, расстояние от z = 0 до фокальной плоскости равно z₀ = 4,1 X . Область моделирования -5 X < x < 5 X; 0 < z < 4 X )

Непосредственно за плоскостью z = z 0 аргументы 5 интегралов Френеля в (24) становятся мнимыми, так как 2 / [ X ( z ₀ - z )] < 0, причём мнимая часть может быть как положительной, так и отрицательной, поэтому возможны два решения, из которых лишь одно удовлетворяет граничному условию E ( x , z ^ z ₀ + 0) = E ( x , z ^ z ₀ - 0) . Используя тождества для интегралов Френеля от мнимых переменных C ( iz ) = iC ( z ) и S ( iz ) = - iS ( z ) [9, выражения 7.3.18], можно показать, что за плоскостью z = z ₀ комплексная амплитуда имеет вид:

E ( x , z >  z 0 ) =

1 J[ 1 + C ( n ) + S ( n ) J -' ² 1- i [ C ( n ) - S ( n ) J J ,

не удовлетворяет граничному условию.

Из сравнения (24) и (27) видно, что световой пучок при z <  z 0 ускоряется, фокусируясь при z = z 0 в равномерное полубесконечное пятно, а амплитуда при z >  z ₀ является зеркальным отражением амплитуды при z <  z ₀, т.е. распространяется с замедлением. На рис. 5 а показана интенсивность светового пучка (24), (27) в плоскости Oxz , а на рис. 5 б показано сечение интенсивности в плоскости z = z ₀. Рис. 5 получен путём расчёта BPM-методом при X = 532 нм, z ₀ = 4 X , область моделирования -20 X <  x < 20 X , 0 <  z < 8 X . Осцилляции интенсивности в окрестности x =0 объясняются ограниченностью начального поля областью моделирования.

X a.u.

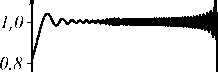
0,2

________x/X

0 H--------1--------1--------1--------1— 1               ■«[ ■i - — 1 »

б)

Рис. 5. Интенсивность светового пучка (24), (27), рассчитанная FDTD-методом: интенсивность в плоскости Oxz (a)

и сечение интенсивности в плоскости z = z0 (б)

Аналогично, заменив в (22) z + z0 на z0 – z и применив комплексное сопряжение, получим световой пучок, комплексная амплитуда которого в начальной плоскости (z =0) равна x T k kx2 1     1 ikx2 1

E ( x , z = ⁰ ) = —J 1 1 — 1 exp l^-— I .       (29)

V z 0 4 I ⁴ z 0 J I ⁴ z 0 J

Задав начальное поле (29), с помощью BPM-метода была рассчитана интенсивность в плоскости Oxz свето- вого пучка (при X=532 нм, z0 = 40X), который, как видно из рис . 6, фокусируется с ускорением. Возникающая при этом асимметрия фокусного пятна объясняется наличием скачка фазы на п/2 у поля (29) в точке x=0. Такая фокусировка с ускорением рассматривалась ранее в [14] для радиально-симметричного пучка Эйри.

z/X

0 --т------------,------------,------------Т------------Т------------,------------,-----------

-20 -15 -10 -5    0    5    10   15   20

Рис. 6. Интенсивность (негатив) в плоскости Oxz ускоряющегося светового пучка с распределением комплексной амплитуды в начальной плоскости (29)

Приравняем нулю амплитуду поля в начальной плоскости при x <0:

E (x, z = 0) = <

x > 0,

^ 0, x <  0.

На рис. 7 показана интенсивность пучка (30), полученная BPM-методом при тех же параметрах, что и на рис. 6.

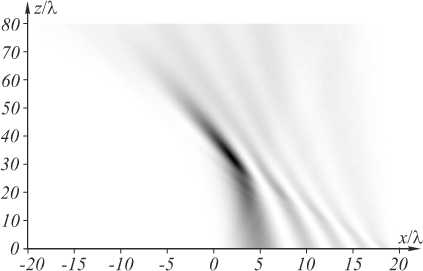
Рис. 7. Интенсивность (негатив) в плоскости Oxz ускоряющегося светового пучка с распределением комплексной амплитуды в начальной плоскости (30)

Для других порядков функции Бесселя в (30) вид картины аналогичный (рис. 8).

Из рис. 8 видно, что с ростом порядка функции Бесселя ускорение падает. Ускоряющиеся параксиальные пучки (30) аналогичны непараксиальным пучкам «половины Бесселя» [2], поэтому будем их называть параксиальными пучками «половины Бесселя ».

Дифракция Гауссова пучка на полубесконечном непрозрачном экране

Рассмотрим ещё пример, когда замедляющийся пучок описывается аналитической функцией. Пусть Гауссов пучок с радиусом перетяжки w проходит через по-лубесконечную плоскую апертуру.

Непосредственно за апертурой комплексная амплитуда будет равна:

E (x, z =

z!X

0-- а)

uz!X

0-- б)

..z/Х

в)

Г x ² I exp -      , x <  0,

I w2)

0, x >  0.

x/X "20"

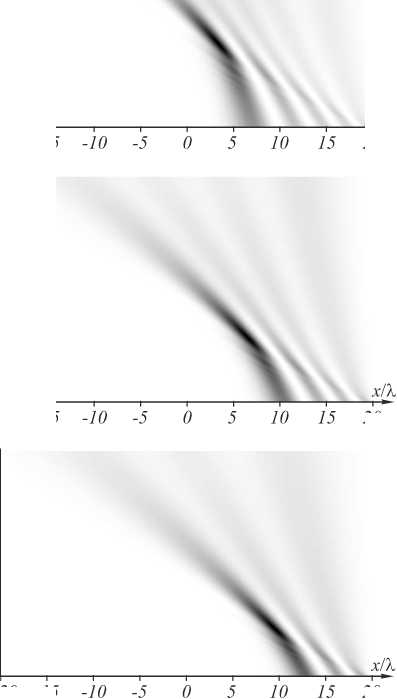
Рис. 8. Интенсивность (негатив) пучка (30) с разными порядками функции Бесселя: 1 (а), 3 (б) и 5 (в)

После прохождения светом расстояния z его комплексная амплитуда будет определяться преобразованием Френеля от поля (31) и примет вид [15]:

E ( x , z ^Eik

8 pz

ikx ²

^exp T(—

L 2 ( Z - iZR ) J

erfc

^ - ikx

12 ^z J

где p = 1 / w ²– ik / (2 z ), z ₀ = kw ² /2 – расстояние Рэлея, erfc ( x ) – дополнительная функция ошибок:

erfc ( z ) = 1 - erf ( z ) = 1 — 2= f exp ( - 1 ²) d t .       (33)

V п J0

Уравнение (32) может быть приведено к виду:

E (x, z)

где

- ik      ( ikx ² |

-j8 pz ^cxp [ 17 J ^{exp (- p} ) ^{erfc ( i}

y =

- kx

2 pz

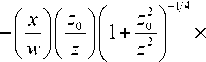
z/k

x exp

■ ¹ +1 z o i — arctg I — 2 I z

При z ^ 0 аргумент переменной y почти не зависит от z : arg (y ) - л /4. Поэтому уравнение траектории та-

кого пучка на малых расстояниях z имеет вид:

max

- ^П m

где n m — m -й максимум функции |erfc[ n ( i -1)] |². Это означает, что, подобно световому пучку (15), пучок (34) будет замедляющимся.

По аналогии с формированием равномерного распределения интенсивности на полуплоскости (с помощью пучка (24), (27)) сформируем распределение (31)

в плоскости z = z ₀ с помощью светового пучка со сле-

дующим распределением комплексных амплитуд:

E (x, z)

ik exp

V 8 Р (z 0 - z)

—ikx

2 ( Z0 - Z + iZR )

1-

x erfc

ikx

2 Vp (z 0 - z)

где p = 1/ w ²+ ik /[2( z ₀– z )]. В (37) в качестве сомножителя входит интеграл вероятности, или интеграл Лапласа. Поэтому будем называть пучки (37) пучками Лапласа. Из вида траектории (36) следует, что пучок (37) также будет ускоряющимся вблизи плоскости z = z 0 . Это можно заметить на рис. 9 а , на котором показана интенсивность пучка (37) в плоскости Oxz . На рис. 9 б показано

сечение интенсивности в плоскости z = z 0 .

Заключение

В работе получены следующие результаты:

– показано, что хорошо известные моды Эрмита– Гаусса и обобщённые пучки Эрмита–Гаусса (8) являются ускоряющимися пучками, то есть два крайних локальных максимума интенсивности, симметричных относительно оптической оси, распространяются по гиперболическим траекториям с неоднородным ускорением, которое уменьшается пропорционально кубу расстояния (12);

– предложен метод преобразования двумерных световых пучков, распространяющихся с замедлением, в ускоряющиеся световые пучки;

– рассмотрен ускоряющийся на конечном отрезке траектории пучок Френеля (24), который получен из комплексной амплитуды, описывающей дифракцию плоской волны на непрозрачном экране (15), путём комплексного сопряжения и сдвига по оптической оси;

– рассмотрен параксиальный ускоряющийся на конечном отрезке пучок «половины Бесселя» (30), который распространяется по траектории корневой параболы и получен из обобщённого гипергеометрического лазерного пучка (21) путём комплексного сопряжения, сдвига по оптической оси и «взятия половины»;

v П-------------- 1--------------1--------------1--------------1--------------1--------------1--------------1-------------- 1--------------1--------------r

а)

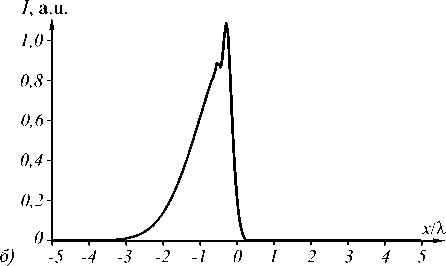
Рис. 9. Интенсивность (негатив) светового пучка (37) в плоскости Oxz (а), а также сечение интенсивности в плоскости z = z0 (б)

– аналогично рассмотрен ускоряющийся на конечном отрезке пучок Лапласа (37), который получен на основе решения (32) задачи дифракции Гауссова пучка на непрозрачном экране путём комплексного сопряжения и сдвига по оптической оси комплексной амплитуды (32).

Работа выполнена при поддержке грантов Президента РФ поддержки ведущих научных школ (НШ-3970.2014.9) и молодого доктора наук (МД-1929.2013.2), а также грантов РФФИ 13-07-97008 и 14-07-31092.