Преобразования эквивалентности уравнений движения двумерного слоя идеальной жидкости

Описание системы уравнений. Многие исследователи нелинейных уравнений давно используют групповой анализ дифференциальных уравнений. Так как принципы инвариантности закладываются при выводе уравнений, применение группового анализа особенно эффективно и плодотворно в области фундаментальной механики и физики [1–4].

В последнее время особо актуальным стало исследование задач математического моделирования разнообразных физических процессов. Главной целью группового анализа является построение точных решений дифференциальных уравнений. На пути построения этих решений важной частью задачи является нахождение преобразований эквивалентности для заданной системы уравнений. В данной работе получены преобразования эквивалентности для системы уравнений, описывающей двумерное движение иде-

альной жидкости, записанных в модифицированных переменных.

Рассмотрим систему уравнений движения двумерного слоя идеальной жидкости по наклонной плоскости. Уравнения запишем в декартовой системе координат так, чтобы ось z была ортогональна к подложке, а ось x направлена в сторону действия скатывающей силы. Жидкость занимает область Q = {( x,z ): -w< x <+от , 0 <  z <  H ( x, t )}, где t - время; H – толщина слоя жидкости. В уравнения движения жидкости входят компоненты вектора скорости ( u , w ), p – давление (скатывающие силы заменой переменных можно включить в давление). Слой жидкости имеет твердую подложку при z = 0 и свободную границу при z = H ( x, t ) (см. рисунок).

Работа выполнена при финансовой поддержке РФФИ, грант 11–01–00238.

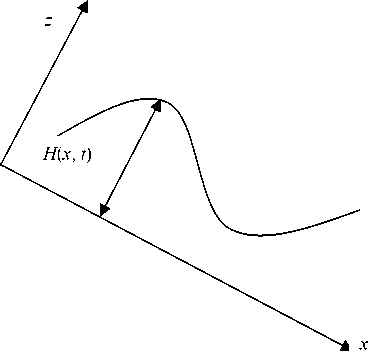
Движение двумерного слоя жидкости толщины H по наклонной плоскости

Решение определяющих уравнений. Поставим задачу группового анализа для уравнений (1)-(4). Необходимо найти преобразования эквивалентности для этой системы уравнений. Преобразования эквивалентности - это преобразования, которые сохраняют структуру исходной системы уравнений [1].

Введем индексные обозначения:

• x ¹ = x , x ² = p , x ³ = t ,

• u ¹ = u , u ² = w , u ³ = p , u ⁴ = H .

Будем считать, что если f ( x 1 , x ², x ³) - некоторая функция, то

f f     8 x¹’ f j

8 ² f

d x d x^j

,

i , j = 1, 2,3.

Система уравнений (1)-(4) перепишется в индексных обозначениях так:

Hu 3 - H ₃ ( u ¹ + x ² u 2 ) + u ¹ u 1 + u ² u 2 -

Рассмотрим систему уравнений движения двумерного слоя идеальной жидкости по наклонной плоскости. Уравнения запишем в декартовой системе координат так, чтобы ось z была ортогональна к подложке, а ось x направлена в сторону действия скатывающей силы. Жидкость занимает область Q = {( x , z ): -го <  x < +го , 0 <  z <  H ( x , t )}, где t - время; H - толщина слоя жидкости. В уравнения движения жидкости входят компоненты вектора скорости ( u , w ), p - давление (скатывающие силы заменой переменных можно включить в давление). Слой жидкости имеет твердую подложку при z = 0 и свободную границу при z = H ( x , t ) (см. рисунок).

В дальнейшем вводятся новые координаты z t = t, x = x, p =--------,

H ( x , t ) модифицированные компоненты вектора скорости и давление [5]:

u = uH , w = w - u p H_x , p = p .

Это позволяет фиксировать границы области по p , Q = {( x , p ): -го <  x < +го , 0 < p <  1} . Система уравнений в новых переменных записывается в виде (черту над переменными опускаем)

р [ Hu t - H_t ( u + p u p ) + uu_x + wu p -

- HH)2 ] = H 2[-Px +^Hxp p ],(1)

p[H(w + S)t -EHt(w+S)p + u(w+S)x + w(w+S)p] = -pp, (2) ux + wp = 0,(3)

Hp = 0,(4)

где p - плотность жидкости (ее можно положить равной единице); S = ( p u ¹ H_x )/ H ; нижние индексы обозначают дифференцирование по x , p , t функций u , w , p . Функция H ( x , t ) и ее производные существенно входят в уравнения (1)-(4), которые образуют замкнутую систему относительно u , w , p .

- —H ( u 1 )² + H ² u ³ - x ² HHu 3 = 0,

H

Hu ₃ ² + x ²( u 1 H + u ¹ H ₃- —

H

- x ² H ₃ ( u ² +-- H ( u ¹ + x ² u 1 )) +

H

+ u ¹ u 2 + u ¹ x ²(— Hu 1 + — H_nu ¹ HH

-

-

7H) +* ^{+ (} H 1 )

+ u ² ( u ₃ +-- H^ ( u + x^u^ )) + u | = 0,

H u1 + u2 = 0, u4 = 0.

Инфинитезимальный оператор, допускаемый темой (5)-(8), ищем в виде [1]

_{v v}i 8 _a 8 x = p ¹ —-+n ^a —, 8 x¹       d u ^a

сис-

где i , а = 1, 2, 3, 4, а координаты оператора p ¹ , n “ зависят от всех зависимых и независимых переменных (по всем повторяющимся индексам производится суммирование).

Поскольку в систему уравнений входят первые производные, то для формирования определяющих уравнений нужно продолжить оператор X на первые производные:

e-dnl+n" dn!

Z' = 5x + ul 5x’

-

в

• ^{z 1} d u e ’

u ,efdp j + u n dp j

• ^j ^ d x ^{1     1} 8 u ⁿ

,

где , , 1 =1, 2, 3 (суммирование по повторяющимся индексам), координаты Z i зависят от всех x ¹ , u ^а и производных u “ . Далее, действуя оператором X на уравнения (8), (7), (6), (5), из критерия инвариантности [1] получаем определяющие уравнения, которые расщепляем по независимым переменным. При этом переходим на многообразие, задаваемое исходными

уравнениями, т. е. u ₃ , u ₃ , u ₂ выражаем через остав-

шиеся элементы и подставляем в определяющие уравнения. Используем также четвертое уравнение u 4 — о.

После достаточно трудоемких выкладок при расщеплении определяющих уравнений относительно независимых переменных получаем следующее представление координат оператора (9):

^ 1 = B 1 х ¹ + C 1 ,

E ² — ( B i - A 4 ) х ²,

Ез — B3 х3 + Cз, n1 = (B1 + A4 - B3) u1, n2 = (Bi - B3)u 2, n3 = (Bi - Bз) u3 + D(х 3),

П ⁴ = A ₄ u⁴ ,

где A ₁ , A ₄ , B ₁ , B ₃ , C ₁ , C ₃ – постоянные; D ( x ³) –

произвольная функция.

Выпишем лентности:

операторы преобразования эквива-

X = —

• ¹     д х 1 ,

X - —

• ²    д х³,

X -X 1 ^д +

X з — х , +

д х

x

д 1 д ₂ д _ ₃ д —~ + u —- + u —— + 2 u —— , д u ¹       д u ²        д u ³

д х

X 4

— X

. 3 д

. i д

X 5

.             ,             2 д

3 - u Г - u 2 д х ³      д u ¹       д u

₂ д 1 д

— - х —— + u —- + u д х ²       д u ¹

-

-

, з д 2 u ₃ , д u

. 4 ^д д u⁴ ’

X б ( D ( х³)) — D ( х³)     .

д u

На основании теоремы Ли для найденных операторов ставится во взаимно однозначное соответствие группа преобразований переменных x ¹ , x ² , x ³ , u ¹ , u ² , u ³ , h . Тем самым доказали, что преобразования эквивалентности для системы (5)–(8) имеют структуру бесконечномерной группы преобразований:

G ^ЭКВ :{ х ¹ — b₃ b ₄ х ¹ + b ,; х ² — b ₃ b ₄ b ₅ ^{- 1} х ²;

33  1122

х — b 4 х + b 2 ;    u — Ь з b ₅ u ; u — Ь з u ;

u ^з — b _з ² u ^з +^ ( х ³); H — b ₅ H },     (10)

где b ₁ , b ₂ , b ₃ , b ₄ , b ₅ – групповые параметры (10), ^ ( х ^з) - произвольная функция. Заметим, что для H в G ^ЭКВ допускается только растяжение с одновре- 21

менным растяжением для x и u .

Автор благодарит своего научного руководителя В. К. Андреева за постановку задачи.