Преобразования плоскости и фракталы

Одним из широчайших полей для приложения знаний и умений по информатике была и остается математика. Это вполне естественно, поскольку информатика имеет достаточно прочный математический фундамент. Но в последние десятилетия и информатика позволила математике сделать новый виток в развитии численных методов, математического моделирования, теории управления и многих других бурно развивающихся направлений современной математики.

Активно развивающимся направлением математики является исследование фракталов и самых различных проявлений фрактальных свойств объектов и систем. В данной статье мы продемонстрируем вариант исследования свойств преобразования плоскости, одним из результатов которого является получение фрактального объекта. Как показывает опыт работы со школьниками, учащиеся вполне способны, пользуясь определенными навыками программирования и методами работы в среде Mathcad, достаточно глубоко изучить свойства не-бычного для школы преобразования плоскости.

Представленный ниже материал может быть использован в качестве блока в элективном курсе или клише при построении учебно-исследовательского проекта, выполняемого школьником. Следует отметить, что при построении элективного курса, одним из разделов которого является исследование нелинейных преобразований плоскости, оптимальным будет использование связей между курсами математики и информатики, прежде всего, для визуализации результатов геометрических преобразований.

В качестве примера исследуем некоторые свойства преобразования плоскости, приводящего к фракталу Жюлиа. Данное преобразование задается следующей системой уравнений:

| x n + 1 = x² - У п ⁺ P 1 ,                                   (1)

l У п + 1 = ^{2 Х} п У п ⁺ P 2 .

Указанное преобразование не является единственным в своем роде. Его аналоги можно встретить при построении алгебраических фракталов и исследовании свойств динамических систем [1]. Поэтому тематика проектной деятельности и элективных курсов может быть достаточно разнообразной при опоре на преобразования плоскости. На преобразовании Жюлиа мы остановили свой выбор прежде всего потому, что его можно представить в очень компактном виде, записав в комплексных переменных:

cn+1 = cn + P.

Здесь c n = x n ⁺ i "  y n и ^p = p i + i ' ^p 2 . Таким образом, появляется возможность варьировать методы исследования данного преобразования в зависимости от уровня подготовки учащихся, области их интересов, спектра изучаемых в курсе математики, включая и элективные курсы, разделов и тем. При этом система уравнений (1) является набором условий для выполнения равенств действительной и мнимой частей уравнения в комплексных числах.

Алгоритм преобразования плоскости должен быть следующим. Для каждой точки исходной плоскости производится бесконечно большое число преобразований координат в соответствии с законами (1) или (2). При этом точка, перемещаясь по координатной плоскости, может либо удалиться на бесконечность, либо остаться в ограниченной области.

Это можно легко продемонстрировать, воспользовавшись графическими средствами редактора Mathcad:

n := 0 .. 8    X q := 0.5     y_Q := 0.5

I xn+11J^-^-0.22

I y n + 1 J       ^2х п У п ^- 0.74

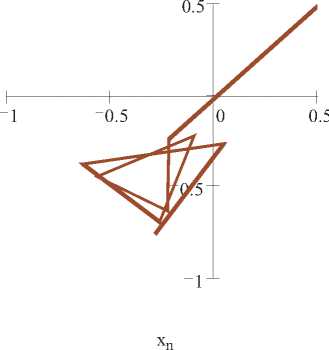
Рис.1. Построение динамики точки в соответствии с преобразованием (1)

Выбирая различные координаты начальной точки, можно получить траектории в виде ломаных линий самого разного типа — от локализованных в небольшой области вблизи начала координат до быстро удаляющихся на бесконечность.

Блиц-анализ системы (1) показывает, что если одна из координат точки в процессе преобразования превышает по модулю 10, то данная точка обязательно уйдет на бесконечность. Число 10 взято в виде достаточно грубого критерия, поскольку точки, вышедшие за окружность, существенно меньшего радиуса с центром в начале отсчета, уже в пределы данной окружности не возвращаются. Данный факт говорит о том, что если появится необходимость определить исходное положение точек, остающихся внутри ограниченной области, или конечное положение остающихся точек, то нам потребуется анализ не всей координатной плоскости, а только достаточно малой прилегающей к началу координат области, что существенно облегчает задачу.

Ограничение исследуемой области на плоскости необходимо для реализации конечных алгоритмов построения образов и прообразов преобразований и является особенно важным шагом для использования средств и методов информатики.

бассейн притяжения. Первое, что можно определить в рамках исследования свойств преобразования (1), – исходное положение точек, которые после бесконечно большого количества примененных к ним итераций по формуле (1) останутся в ограниченной области. Такое множество точек обычно называют бассейном притяжения [2].

Для решения данной задачи мы воспользуемся средой программирования Delphi. Выбор среды программирования должен быть обусловлен языком программирования, изучаемым в курсе информатики. Можно воспользоваться, например, языками Visual Basic или Visual C++, входящими в палитру языков системы MS Visual Studio.

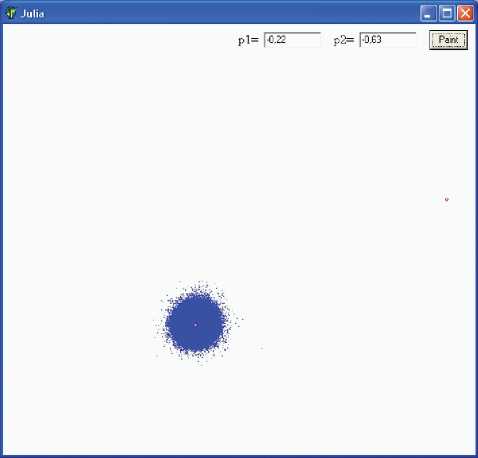
В пустой форме разместим только три объекта: два объекта типа Edit и кнопку, нажатие которой будет инициировать процесс построения бассейна притяжения. Объекты типа Edit необходимы для ввода значений параметров р₁ и р₂ .

Для запуска процедуры построения вводится программный код. Программа представляет собой процесс перебора точек, заключенных в квадратной области от –1,5 до 1,5 по каждой оси, с последующим анализом их динамики при достаточно большом количестве итераций, выполняемых в соответствии с уравнениями системы (1). Если после двухсот итераций точка остается в квадрате, ограниченном условиями | х | <  10 и | у | <  10, то она выводится синим цветом в форму. В противном случае точка в поле рисования остается белой (исходного цвета формы).

Построение подобной программы не должно вызвать особых затруднений у школьников, имеющих понятие об использовании условных операторов и вложенных циклов. Результат работы программы при значениях параметров р₁ = – 0,22 и р₂ = – 0,74 представлен на рис. 1.

Очень важной для понимания учащимися смысла свойства фрактальности объекта представляется демонстрация того, что вид бассейна притяжения может существенно изменяться в зависимости от значений входящих в систему параметров р₁ и р₂. Варьируя их значения, можно проследить за стадиями развития фрактальной структуры бассейна (см. рис.3). Именно для простоты управления значениями параметров р₁ и р₂ необходимо было ввести поля ввода Edit1 и Edit2. Для получения одной картинки достаточно в тексте программы указать значения данных параметров.

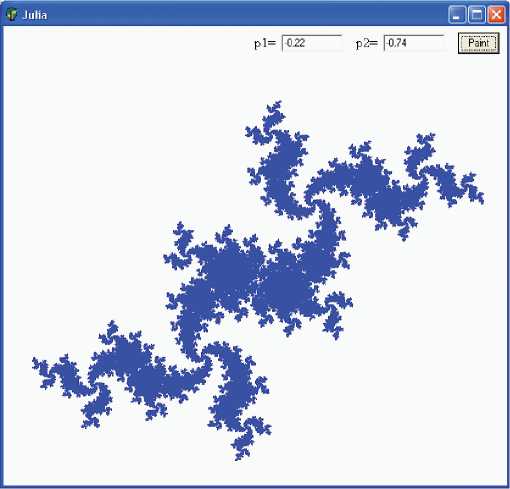
рис. 2. Окно программы, строящей бассейн притяжения

По данному рисунку легко проследить приобретение начальным круговым бассейном фрактальных свойств. Кроме того, подбирая и слабо варьируя параметры, можно наблюдать появление и исчезновение тех или иных особенностей бассейнов притяжения, с которыми можно познакомиться, например, по книге [3].

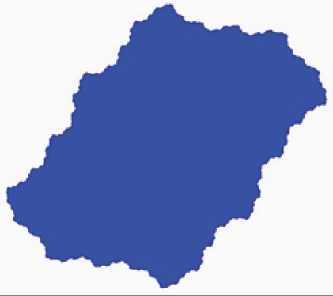
Программу построения легко модифицировать для случая, если понадобится увеличить масштаб изображения, построив лишь часть фрактального множества. Для этого изменяются первая строка вложенных циклов и множитель в строке построения точек (команда Pixels). При этом может получиться картина, подобная представленной на рис. 4.

Пошаговое преобразование плоскости. Рассмотрев метод построения бассейнов притяжения, перейдем к вопросу о непосредственном преобразовании плоскости при пошаговом применении к координатам точек плоскости преобразования, определяемого системой уравнений (1). Данный вопрос представляет интерес при рассмотрении любого типа преобразований плоскости, будь то движение (параллельный перенос, вращение, отражение относительно оси), гомотетия или инверсия. Так, например, при осевой симметрии геометрическая фигура, расположенная на одной полуплоскости, переходит в зеркальную ей фигуру другой полуплоскости. Повторное приложение осевой симметрии с той же осью вернет фигуру в исходное состояние и т.д. Преобразование координат точек при отражении относительно оси ординат на каком-либо шаге будет определяться системой уравнений

X , = — X , п+1         п,

5 I Уп+1 = Уп.

Данная система, описывающая простое преобразование, отличается от системы (1) только по форме, оставаясь, по сути, ее аналогом. Это говорит о том, что принципиальное отличие преобразования плоскости, задаваемого системой (1), состоит лишь в его нелинейности, наличии квадратов и произведения координат в правых частях уравнений системы. Но метод расчета координат образов точек определяется рекуррентными формулами, предполагающими возможность проведения бесконечно большого числа шагов вычислений, итераций.

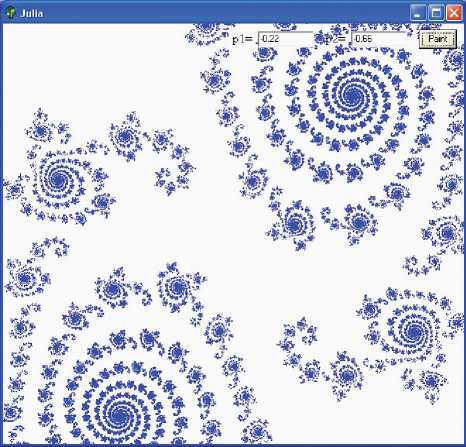
рис. 4. Изменение масштаба построения

Чтобы наглядно представить, как ведут себя точки плоскости при выполнении преобразования (1), следует рассмотреть задачу о преобразовании квадрата, координаты точек которого (x, y) изменяются от –1 до 1. Выберем значения параметров р₁ = –0,22 и р₂ = –0,74.

Нам понадобится некоторая модификация программы. Во-первых, в раздел Public необходимо добавить объявление переменных и массивов:

n: integer;

x,y: array[ 0..1000000] of real.

В теле программы должно быть две процедуры. Одна из них, запускаемая щелчком мыши по форме, строит исходный квадрат. Вторая процедура привязывается к кнопке и позволяет строить образы квадрата на любом шаге преобразований (см. листинг 2 в приложении).

Исходный квадрат и результаты его преобразований представлены на рис. 5.

Таким образом, мы можем сказать, что после применения к квадрату со стороной, равной 2, центр которого совпадает с началом координат, большого числа преобразований, определяемых системой (1), мы получим три скопления точек, близких по форме к окружностям. Совокупность данных скоплений в динамике называется аттрактором (от англ. attraction – притяжение, тяготение), т. е. в результате бесконечного числа преобразований часть точек плоскости удаляется на бесконечность, а часть изначально располагавшихся в бассейне притяжений стремится к аттрактору. Следует отметить, что здесь мы привели решение задачи при конкретных значениях параметров р1 и р2. При других значениях данных параметров поведение образов может существенно варьироваться.

рис.5. Преобразования исходного квадрата неподвижные точки преобразования. Поскольку каждая точка, подвергаясь преобразованию координат, может двигаться по плоскости, пусть даже ее траектория представляет собой ломаную линию (аналог броуновскому движению в физике), то цепь преобразований можно считать динамической задачей.

Для всякой динамической задачи определенный интерес представляют стационарные состояния (в физике такие состояния характеризуются постоянством скорости). В нашем случае стационарное состояние получается при отображении точки в саму себя. При этом система (1) преобразуется к виду

X = X — V + Pi, nnyn  p 1 ,

I Уп = 2 ХпУп + Р 2.

Решения данной системы дадут нам стационарные точки. Для поиска стационарных точек удобнее воспользоваться комплексной формой записи преобразования (2). Тогда:

cn = c2 + P,

СП - cn + P = 0,

D = 1 - 4 p,

получаем решения в виде cn,1 = 2 (1 — V1 — 4P ) и cn,2 = 2 (1 + V1 — 4p ).

Единственную трудность для школьников здесь может представлять выделение в полученном результате действительной и мнимой частей комплексных чисел в явном виде. Для решения данной проблемы мы воспользуемся методом, предложенным в [4].

P i = 0; p 2 = 0

Pi --0,05; p2 --0,1

^p 1 -- 0,1; ^p ₂ -^{- 0,4}

Pi --0,15; p2 --0,6

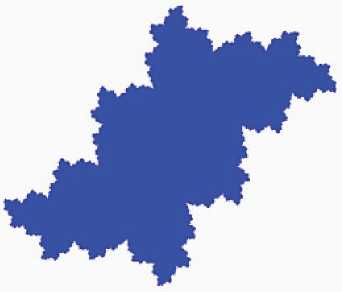
p1 --0,22; p2 --0,63

p1 --0,22; p2 --0,65

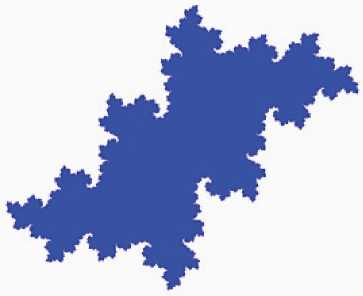
p1 --0,22; p2 --0,66

pi--0,22; p 2--0,7

рис.3. Стадии развития фрактальной структуры бассейна

Пусть - — — 4 p = x + i • y . Тогда, возведя обе части уравнения в квадрат, получаем 1 — 4 p = x ² — y ² + 2 i • xy . Поскольку p = p 1 + i _- p 2 , то наше уравнение распадается на систему уравнений для действительной и мнимой частей:

1 - 4 pi = x2 - y 2, 1^-4 p 2 = 2 xy.

Данная система схожа по внешнему виду с системой (1), но получить ее решение значительно легче. После несложных преобразований получаем два решения:

(dm,-2p2^^27d) и (-VdT2,2p2^^27d).

Здесь мы обозначили d = 1 - 4 p 1 + ^ ( 1 - 4 p 1 ) 2 + ( 4 p 2 ) 2 . Одна из полученных точек является устойчивым центром, к которому стремятся другие точки из бассейна притяжения, а другая – неустойчивым (ситуация аналогична физическому маятнику, имеющему два состояния равновесия). Верность полученного решения легко проверить, модифицировав текст листинга 1. Нам понадобится выводить на экран не точки, остающиеся в ограниченной области, а их образы после достаточно большого (в идеале бесконечного) числа итераций. По окончании счета на полученное множество точек накладываются изображения стационарных точек (см. листинг 3 в приложении).

Заметим, что основная часть кода программы остается прежней. Только в строке вывода точек на экран вместо исходных точек мы будем отображать их образы, полученные в результате 100 итераций. Данное количество итераций выбрано по причине быстрого приближения образов к стационарной точке.

В результате расчетов при значениях параметров р₁ = –0,22 и р₂ = –0,63 получаем скопление точек вблизи равновесной точки (рис. 4). На рисунке стационарные состояния указаны стрелочками.

Очевидно, что поиск стационарных точек является только одной из стадий исследования аттрактора преобразования, поскольку в более сложном случае последний может разделиться на три скопления точек, что говорит о наличии системы центров притяжения, не совпадающей с парой простейших стационарных точек. Но более глубокое исследование свойств преобразования плоскости может потребовать от школьников более серьезного знакомства с теорией комплексных чисел.

Исследование свойств нелинейных преобразований плоскости является проблемой достаточно сложной и емкой по количеству изучаемого материала и времени, необходимому для качественного усвоения темы. Но, как показывает опыт работы со школьниками на базе Волгоградского городского детско-юношеского центра, данная проблема вполне разрешима, если учащиеся имеют навыки программирования и работы в среде Mathcad. Поэтому рассмотрение темы нелинейных преобразований плоскости можно включить в элективный или факультативный курс математики, одной из целей которого была бы демонстрация возможностей вычислительной техники для решения математических задач.

Материал, предложенный в статье, не исчерпывает темы ни со стороны математики, ни со стороны информатики, поскольку он должен служить только основой для последующего развития исследования. Школьникам можно предложить продолжить исследование бассейнов притяжения, применив в качестве инструмента возможность окрашивания точек плоскости в разные цвета в зависимости от вариантов их перемещения. В качестве математической задачи можно предложить вопрос о совпадении корней уравнения (3) и задачу о поиске корней уравнения восьмой степени, возникающей при рассмотрении периодических точек преобразования. Можно предложить исследование других преобразований типа (1). В целом возможный спектр задач очень широк.

Приложение

Листинг 1

procedure TForm1.Button1Click(Sender: TObject); var i,j,k,n:integer;

x,y,x0,y0,x1,y1,p1,p2:real;

label l1;

begin

n:=5000;

for i:=0 to n do for j:=0 to n do begin

x:=-1.5+i*3/n; y:=-1.5+j*3/n;

x0:=x; y0:=y;

for k:=1 to 200 do begin x1 := sqr(x0)-sqr(y0)+p1;

y1 := 2*x0*y0+p2;

if (abs(y1)<10) and (abs(x1)<10) then begin x0:=x1; y0:=y1;

end else goto l1;

end ;

• l1:        if (abs(y1)<10) and (abs(x1)<10) then

end ;

end ;

Листинг 2

//Блок вывода исходного квадрата var i,j:integer;

x1,y1:real;

begin

Canvas.Rectangle(-1,40,601,601);

n:=900;

for i:=0 to n-1 do for j:=0 to n-1 do begin x1:= -1+2*(i/n);

y1:= -1+2*(j/n);

x[n*i+j]:= x1;

y[n*i+j]:= y1;

300-round(y1*100)]:=clBlack;

end ;

end ;

procedure TForm1.Button1Click(Sender: TObject);

//Процедура преобразования точек квадрата var i,j:integer;

x1,y1,p1,p2:real;

begin

Canvas.Rectangle(-1,40,601,601);

for i:=0 to n-1 do for j:=0 to n-1 do begin x1:= sqr(x[n*i+j])-sqr(y[n*i+j])+p1;

y1:= 2*x[n*i+j]*y[n*i+j]+p2;

300-round(y1*100)]:=clBlack;

if (abs(x1)>100) or (abs(y1)>100) then begin x1:=100; y1:=100

end ;

x[n*i+j]:=x1;

y[n*i+j]:=y1

end ;

end ;

Листинг 3

procedure TForm1.Button1Click(Sender: TObject);

var i,j,k,n:integer;

x,y,x0,y0,x1,y1,q1,q2,p1,p2:real;

label l1;

begin

n:=5000;

for i:=0 to n do for j:=0 to n do begin

x:=-1.5+i*3/n; y:=-1.5+j*3/n;

x0:=x; y0:=y;

for k:=1 to 100 do begin x1 := sqr(x0)-sqr(y0)+p1;

y1 := 2*x0*y0+p2;

if (abs(y1)<10) and (abs(x1)<10) then begin x0:=x1; y0:=y1;

end else goto l1;

end ;

l1:        if (abs(y1)<10) and (abs(x1)<10) then

end ;

//Блок вывода стационарных точек

q1:=0.5*(1+sqrt(1-4*p1+sqrt(sqr(1-4*p1)+ sqr(4*p2)))/sqrt(2));

q2:=-sqrt(2)*p2/sqrt(1-4*p1+sqrt(sqr(1-4*p1)+ sqr(4*p2)));

Canvas.Ellipse(300+round(q1*200)-2,

300-round(q2*200)-2,300+round(q1*200)+2,

300-round(q2*200)+2);

q1:=0.5*(1-sqrt(1-4*p1+sqrt(sqr(1-4*p1)+ sqr(4*p2)))/sqrt(2));

q2:=sqrt(2)*p2/sqrt(1-4*p1+sqrt(sqr(1-4*p1)+ sqr(4*p2)));

Canvas.Ellipse(300+round(q1*200)-2,

300-round(q2*200)-2,300+round(q1*200)+2,

300-round(q2*200)+2);

end ;