Прерывистая текучесть: физические механизмы, экспериментальные данные, макрофеноменологические модели

Прерывистая текучесть (ПТ), называемая также скачкообразной деформацией, – явление неустойчивости пластического деформирования, которое обнаруживается практически для всех сплавов в определенных температурно-скоростных диапазонах деформирования. Прерывистая текучесть проявляется на деформационных кривых в виде повторяющихся неоднородностей – ступенек или зубцов различного типа и имеет ряд общих закономерностей для различных материалов и температур. В большинстве работ по данной тематике ПТ связывают с макро- и мезолокализацией деформации, которая для моно- и поликри- сталлических металлов и сплавов проявляется в виде полос сдвига. Следы полос сдвига на поверхностях готовых изделий существенно увеличивают шероховатость поверхностей, снижают усталостную прочность и коррозионную стойкость. В связи с этим актуальной является проблема установления диапазонов воздействий, в которых реализуется прерывистая текучесть, для их исключения в технологических режимах обработки металлических изделий (по крайней мере – на финишных операциях).

При деформировании материалов в условиях высоких температур активно протекают конкурирующие неравновесные процессы, связанные с упрочнением и разупрочнением. Основной вклад в упрочнение вносит увеличение в металле плотности дислокаций, их взаимодействие друг с другом и иными дефектами кристаллической решетки. В отсутствие фазовых переходов разупрочнение в сплаве происходит за счет динамического возврата, полигонизации и рекристаллизации (впрочем, данные процессы с позиций механики тоже можно рассматривать как разновидности фазовых превращений).

Нарушение монотонности температурной зависимости и чувствительности к скорости деформации механических свойств (в особенности – напряжения течения) при неупругом деформировании при простых и сложных нагружениях обнаруживается в сплавах на основе железа – углеродистых и легированных сталях, интерметаллидах и других сплавах. Экспериментальные методы исследования рассматриваемого явления чрезвычайно ресурсоемки (особенно – в испытаниях на сложное нагружение) и применимы только для уже существующих материалов. Наиболее предпочтительными для анализа прерывистой текучести, определения оптимальных режимов обработки, проектирования новых материалов являются методы и подходы, основанные на математическом моделировании. Построение математических моделей, с достаточной степенью адекватности отражающих исследуемые процессы, невозможно без тщательного изучения имеющейся эмпирической информации, установления лидирующих физических механизмов, чему и посвящена основная часть предлагаемого обзора.

Из имеющихся экспериментальных данных хорошо известно, что температура и скорость деформации оказывает значительное влияние на процессы деформирования. Для большинства поликристаллов в условиях отсутствия фазовых переходов повышение температуры и уменьшение скорости деформации ведет к снижению напряжения сопротивления неупругой деформации. Влияние скорости и температуры деформирования на поведение материалов в реальных процессах отражены в работах [47, 71, 72, 73 и др.]. Влияние температуры и скорости деформации на отклик материала существенно зависит от режима их изменения, типа кристаллической решетки, дефектной структуры.

Выдержка поликристаллов после предварительной пластической деформации при повышенных температурах (0,1÷0,2) Т Г ( Т Г – гомологическая температура, равная отношению температуры процесса к температуре плавления материала в кельвинах) приводит к значительному повышению напряжения течения при последующем пластическом деформировании. Данное явление носит название старения и обусловлено «закреплением» дислокаций диффундирующими к ним атомами «примесей».

Среди эффектов, связанных с деформационным статическим (ДСС) и динамическим старением (ДДС), отметим следующие: возникновение «зуба текучести» на диаграмме деформирования, повторное его появление, качественная зависимость «зуба» от жесткости нагружающей системы и прерывистая текучесть, которая в большинстве работ связывается с эффектом Портевена–Ле Шателье (ПЛШ).

Физические процессы, обусловливающие ДСС и ДДС в сплавах, приводят к изменению микроструктуры, что отражается на макросвойствах продукции. Поэтому для понимания и моделирования процессов, происходящих в ходе деформации материала, необходимо знать термомеханические условия возникновения ДСС и ДДС, связи физических механизмов старения с другими механизмами упрочнения и разупрочнения.

Старение и диффузионные эффекты

Существенное отличие поведения сплавов от реакции чистых металлов на различные воздействия хорошо известны и эксплуатируются человечеством уже в течение столетий. Большинство используемых в промышленности сплавов образуются на основе некоторого основного металла (например, в сталях – железа), остальные компоненты могут составлять от десятых (и сотых) долей до десятков процентов атомной массы; в дальнейшем атомы последних будут называться «примесными». Многообразие свойств сплавов порождается не только разнообра- зием физико-химических взаимодействий и микроструктуры, возникающих на стадии образования материала (например, кристаллизацией из расплавов), но и процессами, происходящими на стадиях последующей термомеханической обработки заготовок. Для рассматриваемой в предлагаемой работе прерывистой текучести к классу наиболее важных из них следует отнести диффузионные процессы, изучению и описанию которых посвящено огромное число работ, включая классические монографии по физике твердого тела [14, 16]. Значительная часть работ по данному направлению посвящена различным аспектам и результатам экспериментальных исследований.

Изложению методики и результатов экспериментального исследования процесса статического старения образцов из эвтектоидной стали, полученных волочением при больших (более 3) степенях обжатия, посвящена статья [75]. Для экспериментального анализа использованы дифференциальная сканирующая калориметрия и термоэлектрические методы. На основе результатов экспериментов утверждается, что процесс старения можно разделить на две стадии. На первой в окрестности дислокаций в ферритной фазе стекаются атомы углерода, расположенные в междоузлиях решетки железа, однако в силу малой концентрации углерода в феррите этот процесс быстро исчерпывает себя; при этом отмечается, что локальная равновесная концентрация зависит от плотности дислокаций, повышаясь с возрастанием плотности дислокаций. На второй стадии имеет место диссоциация мартенсита и диффузия атомов углерода в окрестности ядер дислокаций до достижения в них локально равновесной концентрации.

Результаты термомеханических испытаний, проведенных на образцах из титанового сплава (Тi-Al), обсуждаются в [56]. Образцы подвергались предварительному обжатию на 0,6–3,4 % со скоростями деформации 10–5–10–4 с–1, после чего разгружались до различных значений напряжений (от 2/3 до 1/10 напряжения течения) и выдерживались при температурах от 200 до 500 °С. При дальнейшем нагружении наблюдалось существенное повышение напряжения течения с последующим резким падением последнего, что объясняется эффектами статического старения. Показано, что на величину повышения напряжения существенно влияет температура и продолжительность выдержки, тогда как уровень напряжений, поддерживаемый в процессе старения, практически не сказывается на величине повышения напряжения течения.

Результаты механических испытаний на одноосное симметричное циклическое деформирование цилиндрических образцов из нержавеющей стали 316L(N) для оценки влияния динамического деформационного старения на усталостную прочность приведены и обсуждаются в [67]. Опыты проведены для широких диапазонов изменения амплитуды деформаций (0,25–1,0 %), скоростей деформации 3·10–5– 3·10–2 с–1 и температур (298–873 К). Результаты экспериментов показывают, что динамическое старение, имеющее место в интервале температур 673–873 К, существенно снижает усталостную прочность. Результаты аналогичных исследований применительно к аустенитной нержавеющей стали (15Cr–15Ni–2,5Mo), модифицированной титаном, представлены в [64].

Данные экспериментальных механических и микроструктурных (с использованием электронной микроскопии) исследований влияния температуры, времени выдержки и скорости охлаждения на процесс статического старения приведены в [68]. Эксперименты проведены на четырех марках ультранизкоуглеродистых (с содержанием углерода 0,0032–0,0052 %) сталях при температурах отжига 750–920 °С. Влияние старения на механические свойства оценивалось по повышению предела текучести («зубу текучести»). Результаты подобных исследований, проведенные на образцах из сплавов Al–Mg, приведены в [28]. Особое внимание уделено влиянию на вязкость и пластичность сплавов легирующих добавок бора.

Результаты детальных экспериментальных исследований возникновения и распространения полос Людерса в трубчатых образцах из стали 1045 (С – 0,487, Si – 0,28, Mn – 0,74 %), подвергаемых растяжению, кручению и комбинированному нагружению (лучевые траектории и траектории с изломом на 90о) при комнатной температуре, представлены в [81]. Образование полос Людерса объясняется отрывом дислокаций от атмосфер Коттрелла и резким увеличением их плотности. Описаны особенности распространения полос в зависимости от вида траектории деформации.

В [36] для исследования влияния эффектов деформационного старения на поведение алюминиевых сплавов предложено использовать опыты на простое циклическое нагружение при различных температурах (–20, 20 и 60 °С) и различных способах предварительной термической обработки образцов. Часть образцов обработана на макси- мальное предварительное старение при повышенных температурах, при котором атомы примесей образуют дискретно распределенные частицы вторичной фазы. Другая серия образцов была подвергнута так называемому естественному старению при комнатной температуре. Далее образцы обеих групп подвергались циклическому нагружению при фиксированной амплитуде деформации (±0,6 %). Показано, что образцы первой группы обнаруживают быстрое начальное повышение амплитудных значений напряжений с последующим их монотонным уменьшением. Разупрочнение авторы объясняют перерезанием частиц жесткой фазы движущимися дислокациями и образованием полос скольжения. Образцы второй группы показали монотонное повышение амплитудных напряжений (вплоть до образования трещин), причем тем бóльшее, чем выше температура испытаний. Указанное упрочнение объясняется влиянием динамического деформационного старения за счет диффузии атомов примесей, равномерно распределенных в материале (твердом растворе).

Результаты экспериментального исследования влияния динамического деформационного старения на особенности формирования текстуры различных слоев прокатываемого листа из низколегированного хрома: содержание легирующих элементов La, Ti, Nb, Ta – в пределах 0,2–0,5 %, примесных атомов С, О, N – 0,008–0,01 % [59]. Показано существенное изменение распределения текстуры по толщине листа в зависимости от режима обжатий, что, по мнению авторов, объясняется влиянием последних на диффузионные потоки примесных атомов, приводящих, в свою очередь, к различию в реализации консервативной и неконсервативной мод движения дислокаций.

В работе [3] экспериментально изучено влияние динамического деформационного старения сплава АМг6 на сопротивление пластической деформации в диапазоне температур 300–500 °С и скоростей деформации 0,1–4 с–1. Проведены металлографические исследования сплава АМг6 с целью выявления основных механизмов упрочнения и разупрочнения в исследуемом температурно-скоростном диапазоне. Металлографическими методами исследования показано, что в сплаве АМг6 имеет место динамическое деформационное старение в ходе деформации, которое приводит к выделению интерметаллидов из матрицы твердого раствора при температуре испытания 400 °С; установлено, что в сплаве АМг6 в результате выдержки при температуре 400 °C происходит частичное растворение выделений интерметаллидов.

Результаты механических испытаний по монотонному и циклическому одноосному нагружению образцов из нержавеющей стали при постоянных и циклически изменяющихся температурах приведены в [78]. Температуры испытаний варьировались в пределах 293–823 К, скорости деформации 10–5–10–3 с–1. Из анализа результатов экспериментов следует, что при низких температурах материал обнаруживает высокую чувствительность к скорости деформации, которая уменьшается с ростом температуры, возникновением в определенном диапазоне температур прерывистой пластичности; с увеличением температуры наблюдается также увеличение циклического упрочнения. Отмечается, что указанные эффекты отражают (среди других механизмов) влияние динамического деформационного старения. Для теоретического описания используется макрофеноменологическая термовязкопластическая модель с комбинированным законом упрочнения, в котором изотропное упрочнение учитывает деформационное старение, а в законе кинематического упрочнения фигурируют две составляющие остаточных микронапряжений («обратных напряжений»), отвечающие за близко- и дальнодействующие поля напряжений.

Методы и результаты исследования влияния выделений (второй фазы) на механические характеристики и анизотропию пластических свойств при одноосном растяжении состаренного сплава Al-Mg-Si представлены в [19]. При построении модели широко используются ранее полученные результаты других исследователей, в частности аналитические решения задач зарождения и роста включений. Для описания деформирования применяется упруговязкопластическая модель со степенным законом течения. В соотношении для критических напряжений сдвига по системам скольжения (СС) учтено влияние включений и растворенных атомов легирующих элементов (для рассматриваемого сплава – Mg и Si); упрочнение определяется плотностью дислокаций, эволюционное уравнение для которой также включает зависимость параметров уравнения от концентрации атомов легирующих примесей и включений. Для реализации использована прямая модель (2-го типа) [13], встроенная в пакет ABAQUS. Сопоставление теоретических результатов с данными проведенных авторами экспериментов обнаруживает удовлетворительное соответствие.

Эффект Портевена–Ле Шателье

Основываясь на моделях физики твердого тела и имеющихся экспериментальных данных, можно констатировать, что все процессы деформирования, в которых велика роль диффузионных процессов (диффузия точечных дефектов, неконсервативное движение («переползание») дислокаций и др.), чувствительны к скорости деформации и температуре [13]. В качестве одного из наиболее известных проявлений влияния диффузионных процессов на поведение деформируемого материала является эффект Портевена–Ле Шателье (Савара–Массона).

Следует напомнить, что в зависимости от применяемого способа нагружения различают два вида механических испытаний: «жесткое» (кинематическое) и «мягкое» (силовое) нагружение. В первом случае задается скорость траверсы, и измеряется силовой отклик системы. Во втором случае задаются внешние силовые факторы (например, величина деформирующего усилия), и измеряется кинематический отклик материала.

Эффект Портевена–Ле Шателье с точки зрения макроэкспериментов на одноосное нагружение проявляется в следующем: при низких скоростях деформирования и повышенной температуре диаграмма σ - ε приобретает пилообразную форму («зубчики») при «жестком» нагружении; при «мягком» нагружении диаграмма становится ступенчатой (рисунок) [1, 2].

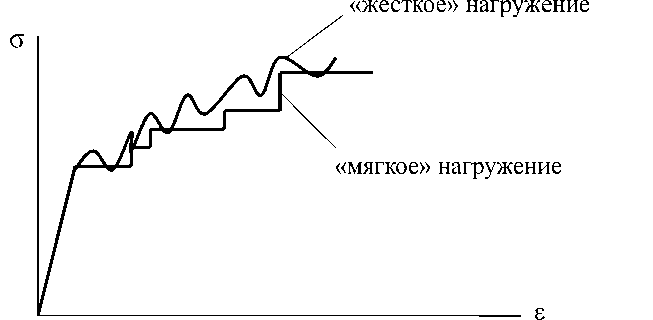
Рис. Диаграммы одноосного «жесткого» и «мягкого» нагружений

Первоначально открытие данного эффекта принадлежит Ф. Савару (1837) и А. Массону (1841) [1, 2], однако работам этих исследователей не было уделено должное внимание, и позднее (1923)

эффект был «переоткрыт» А. Портевеном и Ф. Ле Шателье [61], чьими именами он и называется в большинстве современных работ. Справедливости ради отметим, что в отличие от Савара и Массона Портевен и Ле Шателье изначально ставили своей целью изучение именно прерывистой пластичности. Для решения этой задачи они использовали образцы из сплавов (алюминий + 4,5% меди) и (алюминий + 4,5% меди + 0,5% магния); испытания проводились в машине кинематического типа (жесткое нагружение) при скоростях деформации 0,08 мин–1.

Данный эффект изучался многими исследователями (К. Элам, Т. Сутоки, Э.А. МакРейнольдс, О.В. Диллон, У.Н. Шарп и др.). В экспериментальных исследованиях была установлена зависимость амплитуды зубцов от величины температуры и температурной предыстории (Сутоки), влияние на эффект Портевена–Ле Шателье чистоты металлов, волнообразный характер перемещения по образцу ступеньки деформации (МакРейнольдс). В настоящее время существует несколько объяснений эффекта Портевена–Ле Шателье. Одно из первых было высказано А.Г. Коттреллом [30], который объяснял эффект диффузией примесных атомов к дислокациям и их «закрепление» за счет взаимодействия с атомами примеси [14, 16]. Следует отметить, что на этой точке зрения стоят многие современные исследователи эффекта ПЛШ (см., например, [22, 33, 39, 45, 50, 53, 57, 58, 62, 70] и содержащиеся в них обширные списки литературы). Б.М. Лемприер (1962) объяснял эффект нестабильностью скорости деформирования для некоторых материалов и колебаниями испытательной машины; необходимость учета жесткости экспериментальной установки отмечается также в статье [53]. В настоящее время ни одна из этих гипотез не является превалирующей и доказанной экспериментально, в силу чего отсутствуют и модели, с высокой степенью адекватности описывающие данный эффект для различных материалов и условий нагружения.

Материалы, демонстрирующие прерывистую ползучесть, можно разделить на две группы по масштабному признаку этого явления. К первой группе относятся материалы, проявляющие макроскопическую прерывистую ползучесть. Наиболее известным примером локализации деформации на макроскопическом уровне является возникновение шейки на заключительном этапе растяжения образца [10, 12,15], полосы Людерса–Чернова. Макроскопическая прерывистая ползучесть наблюдается в металлах и сплавах, склонных к эффекту Портеве- на-Ле Шателье [61], поликристаллических сплавах систем Al-Cu, Al-Mg [1,2,52], Ni-Cr, Ni-Fe-Cr [40–42].

Ко второй группе относятся материалы, демонстрирующие мезоскопическую прерывистую ползучесть, связанную с динамикой дислокационных скоплений на мезоскопическом структурном уровне (линии и полосы скольжения, двойники и т.д.). Прерывистая ползучесть в этом случае проявляется в виде последовательности скачков деформации на кривых ползучести. К этой группе материалов относятся монокристаллы цинка, льда, щелочно-галоидные монокристаллы, поли-кристаллическая латунь, медь, свинец, а также ряд полимеров.

Обычно эффект ПЛШ наблюдается в ряде разбавленных растворов внедрения и замещения (сплавов алюминия, меди, мягких сталей), некоторых металлических композитах [11,31], причем для каждого материала эффект проявляется в определенной температурно-скоростной области [6, 7]. Этим температурно-скоростным областям проявления эффекта Портевена–Ле Шателье отвечают обратная скоростная и аномальная температурная зависимости напряжения течения, т.е. с ростом скорости деформирования напряжение течения не увеличивается, а уменьшается, а с повышением температуры напряжения течения остаются либо независимыми от ее увеличения, либо повышаются.

Экспериментальные исследования

Экспериментальные данные, свидетельствующие о немонотонном отклике при монотонном неупругом деформировании или нагружении образцов, были обнаружены достаточно давно. Выше уже отмечены работы Савара [65], Массона [49], Портевена–Ле Шателье [61], своеобразные кривые деформирования приведены в экспериментах Монтелье [55].

При малых и больших деформациях этот эффект изучался последние два столетия многими экспериментаторами и теоретиками (К. Элам, Т. Сутоки, Э.А. МакРейнольдс, О.В. Диллон, У.Н. Шарп и др.), однако удовлетворительного объяснения и описания до настоящего времени не получил.

Нерегулярности диаграммы напряжение-деформация для растягиваемых металлических образцов впервые описал Дюло в 1813 г. [2]. Ступенчатые зависимости в случае «мягкого» нагружения известны с 1837 г. как эффект Савара–Масона.

Массон описал крутой, почти вертикальный (на диаграмме σ–ε) рост напряжений, сопровождавшийся очень малой деформацией, вплоть до значения, при котором происходило внезапное резкое увеличение деформации при постоянном напряжении (эффект лестницы).

Портевен и Ле Шателье в 1923 г. проводили испытания образцов из сплавов (алюминий + 4,5% меди) и (алюминий + 4,5% меди + 0,5% магния) в машине кинематического типа (жесткое нагружение) при скорости деформации 0,08 мин–1. Они обнаружили зубчатую прерывистость и эпизодически возникавшие внятные звуки, связанные с появлением каждой ступени прерывистости [2].

В 1949 г. МакРейнольдс выяснил [52], что образование каждого горизонтального участка графика обусловлено прохождением по образцу медленной «волны».

С позиций А.Г. Коттрелла рассматривается эффект ПЛШ в твердых растворах замещения (на примере V–С) в работе [77]. На основе качественного рассмотрения взаимодействия примесных атомов с дислокациями получены оценки интервалов скоростей деформирования и температур, в которых проявляется эффект ПЛШ.

Интерес к экспериментальным исследованиям эффекта Портеве-на–Ле Шателье не затухает и у современных исследователей. Следует отметить, что большинство экспериментов реализованы для случая одноосного нагружения плоских или цилиндрических (с круговым поперечным сечением) образцов. На основе имеющихся экспериментальных данных по одноосному нагружению выделены три основных типа проявление эффекта ПЛШ: 1) тип А – появление и движение вдоль оси образца одиночной (уединенной) волны, которое может происходить многократно; 2) тип В – деформационные полосы появляются и исчезают в осциллирующем или перемежающемся режиме, распространяясь вдоль образца (stop-and-go); 3) тип С – полосы возникают (и пропадают) случайным образом по длине образца. Как и каждая классификация, приведенная выше является в определенной мере условной; в реальных опытах наблюдается и различное сочетание этих трех типов.

Результаты экспериментальных исследований неупругого деформирования титановых сплавов (Тi – 15% Мо и Тi – 25% Мо) в широком диапазоне температур и скоростей деформации представлены в [20]. Для сплава Тi – 15% Мо в опытах на одноосное растяжение обнаружена прерывистая пластичность при температурах 575–775 К и скорости деформации 1,31×10–4 с–1; с использованием электронной микроскопии проведены исследования структуры на разных стадиях деформирования образцов. На различных масштабных уровнях (от десятков нм до мм) детально описываются процессы деформирования, ответственные за прерывистую пластичность. Для рассматриваемых сплавов основным механизмом прерывистой пластичности является чередующееся возникновение и разрушение (полосами сдвига) частиц ω-фазы в окружении устойчивой β-фазы. Отмечается, что в сплаве Тi – 25% Мо, не склонного к образованию ω-фазы, во всем рассматриваемом температурно-скоростном диапазоне деформирование реализуется монотонно.

Результаты многочисленных экспериментов, направленных на исследование прерывистой пластичности, позволяют сделать вывод, что источником прерывистого, нерегулярного отклика материала при монотонных воздействиях является наличие неоднородностей свойств материала и особенностей движения больших массивов дислокаций (т.е. их согласованных движений) на различных масштабных уровнях, от наноразмеров до величин, соизмеримых с размерами макрообразцов. При этом указанные неоднородности сами могут возникать и исчезать вследствие происходящих в материале процессов движения и взаимодействия дефектов различной природы и размерности.

Методика и анализ результатов экспериментального исследования прерывистой пластичности в образцах из алюминидов титана представлены в [60]. Испытания на одноосное сжатие проведены в условиях вакуума при температурах 20–500 °С и скорости деформации 2·10–3 с–1 для сплава TiAlNb, 20–900 °С и 5·10–4 с–1 – для сплавов TiAlMo и TiAlMoNb. На основе исследования различных количественных композиций сплавов устанавливается, что эффект ПЛШ наблюдается в сплавах, в которых нарушено стехиометрическое соотношение для атомов Ti, при выполнении которого (или при меньшем количестве атомов титана) атомы титана занимают вполне определенные места в кристаллической решетке. Избыточные атомы титана образуют примесные облака вокруг дислокаций, взаимодействие с которыми и обусловливает нерегулярный характер деформирования.

Результаты экспериментальных исследований поведения образцов из сплава Al–2,03% Mg–1,13% Cu–0,95% Zn содержатся в [80]. Эксперименты проведены на плоских образцах длиной 20 и 50 мм в условиях одноосного растяжения, комнатной температуры, в широком диапазоне изменения скоростей нагружения (7,6·10–4–10,5 МПа с–1). Эффект ПЛШ связывается авторами с формированием и распространением полос сдвига. Отмечается существенное влияние на кинетику полос сдвига наличия концентраторов напряжений, скорости нагружения и длины образца.

Результаты систематических исследований поведения образцов из сплавов Cu+Al и Cu+Mn при одноосном нагружении в широком диапазоне температур и скоростей деформации приведены в [57, 58]. На основе анализа диаграмм одноосного растяжения (кривых σ–ε) построены диаграммы областей устойчивого и неустойчивого (прерывистого) неупругого деформирования; отмечается наличие трех характерных областей параметров процесса, в которых проявляется эффект ПЛШ. По мнению авторов, отличие процессов динамического деформационного старения в трех указанных областях обусловлено различием механизмов диффузии («решеточной» (нормальной) и «туннельной» диффузии).

Результаты экспериментальных исследований влияния на прерывистую пластичность содержания азота в аустенитной нержавеющей стали 316L приведены в [39]. Испытания проводились на цилиндрических образцах, подвергаемых одноосному растяжению с постоянными скоростями деформирования в диапазоне (2·10–4–10–2) с–1 при температурах 293, 373, 573, 673, 773, 883 и 973 К. Содержание азота изменялось в пределах (0,01–0,15 %). Показано, что область прерывистой пластичности смещается в сторону более высоких температур с ростом содержания азота. Повышение концентрации азота до температур 773 К ведет также к увеличению критической накопленной деформации начала прерывистой пластичности, при более высоких температурах рост содержания азота не сказывается на критической деформации. Отмечается также увеличение энергии активации динамического деформационного старения с увеличением концентрации азота.

Анизотропия эффекта ПЛШ для листовых алюминиевых сплавов подтверждена результатами экспериментальных исследований, приведенными в [29]. Испытания проведены на образцах из Al-Mg-сплава AA5182, полученных непрерывной разливкой (НЛ) и литьем в изложницы (ЛИ) с последующими горячей и холодной прокаткой и различными видами термообработки. Полученные для испытаний образцы существенно отличались по микроструктуре: образцы из НЛ-сплава имели примерно равноосное зерно без выраженной текстуры, тогда как ЛИ-образцы обладали вытянутой в направлении прокатки формой зерен и текстурой. Эксперименты проведены на образцах, вырезанных в направлении прокатки, поперечном направлении и под углом 45° к направлению прокатки, подвергаемых кинематическому растяжению (жесткое нагружение). В качестве основной характеристики прерывистого течения использовался закон распределения амплитуды скачков напряжений (доли скачков, имеющих определенное значение амплитуды). Показано, что для НЛ-образцов законы распределения амплитуды скачков напряжений практически одинаковы для различных образцов, тогда как для ЛИ-образцов эти законы существенно отличались. Авторы объясняют эффект анизотропии концентрацией атомов примеси преимущественно вдоль границ зерен, создающей облегченные условия для скольжения дислокаций вдоль направления удлинения зерен.

Результаты экспериментальных исследований по растяжению образцов из поликристаллов сплава Al–Mg и монокристаллического сплава Cu–Al приведены и анализируются в [24]. Опыты проведены при комнатной температуре в широком диапазоне скоростей деформирования (5,56·10–6–1,39·10–2) с–1. Поликристаллические образцы имели различную структуру: в состоянии поставки (после прокатки), получаемую после отжига и глубокого отжига. Во всем диапазоне исследуемых скоростей деформации реализовывались режимы прерывистой пластичности. Для обработки результатов измерений использовались методы хаотической динамики и фрактального анализа. Обнаружено, что при средних скоростях деформирование имеет хаотический характер (полосы сдвига типа С), а при высоких скоростях наблюдается переход к самоорганизованной критичности (полосам скольжения типа В и А).

В [43] приведены результаты испытаний по индентации и растяжению образцов из алюминиевого сплава (3,6 Mg, 0,39 Mn, 0,30 Fe, 0,16, Si, 0,076 Cu, 0,072 Cr, 0,031 Zn, 0,018 Ti, 0,014 Zr в мас. %) при комнатной температуре. Использованы инденторы конической, пирамидальной и цилиндрической формы. Показано удовлетворительное соответствие результатов во всех опытах. Отмечается переход к «стационарному» режиму прерывистой пластичности (т.е. примерно одинаковым скачкам напряжений при продолжающемся монотонном нагружении) при больших деформациях.

Значительный интерес (особенно с точки зрения идентификации и верификации моделей эффекта ПЛШ) представляет работа [69], в которой приведены результаты экспериментального исследования поведения подвергаемых одноосному растяжению при низких скоростях (10^–4, 10^–3, 5·10^–3 с^–1) образцов из сплава Al–Cu. Образцы были подвергнуты термообработке на твердый раствор (нагрев и выдержка в течение 3 часов при температуре 500 °С, охлаждение в печи и выдержка при температурах 500, 400, 300, 200 и 100 °С с последующей закалкой). Для сравнения одна из серий образцов была подвергнута отжигу (выдержка в течение 2 часов при температуре 500 °С и медленное охлаждение в печи). Повышение температуры обработки ведет к повышению концентрации Cu в твердом растворе, снижение температуры способствует образованию локальных зон выделений Cu и формированию включений CuAl 2 , что отражается на поведении макрообразцов. Показано, что с ростом температуры обработки наблюдается переход от полос сдвига типа С к полосам типа В с одновременным ростом амплитуды напряжений прерывистой пластичности.

Приведенные в [74] результаты экспериментов по растяжению цилиндрических образцов из магниевого сплава (94,7% Mg, 4,32% Li, 0,97% Al) при скоростях деформации 3,33·10–4, 6,66·10–4, 3,33·10–3, 6,66·10–3 с–1 и комнатной температуре демонстрируют отрицательную скоростную чувствительность и прерывистую пластичность для указанных параметров процесса деформирования. Указанные особенности поведения сплава авторы объясняют диффузией атомов Li и Al к скоплениям дислокаций на различных барьерах дислокационной природы.

Методика и результаты экспериментального исследования образцов из сплава 3033 (Al–Mn) при одноосном сжатии до значений истинной (логарифмической) деформации 80 % представлены в [33]. Испытания проведены в широких диапазонах скоростей деформации (от 10–3 до 104 с–1) и температур (от 77 до 800 К). Отмечается существенное влияние на микроструктуру и поведение материала истории температурных воздействий, накопленной пластической деформации и скорости деформации. Показано, что прерывистая пластичность, проявление которой связывается с деформационным старением, может иметь место даже при высоких скоростях деформации в условиях повышенной температуры. На основе физического анализа и рассмотрения экспериментальных данных предложена модификация соотношения для оп- ределения напряжения течения, в котором, однако, в явном виде не отражено влияние деформационного старения.

В работах [8, 9, 17, 18] установлено, что скачкообразная деформация сплава АМг6 является структурно-чувствительным эффектом. В [8, 9] выявлена зависимость начальной деформации появления скачков от размера зерна после интенсивной пластической деформации. Характеристики скачкообразной деформации, особенно количество скачков, подвижность и морфология первых полос деформации, резко меняются после отжига в окрестности температуры ограниченной растворимости магния в алюминии TSV ≈ 275 °C [17, 18].

Детальное изложение методики и результатов тщательно выполненных экспериментов (включая исследования с помощью электронной микроскопии) по одноосному растяжению образцов из магниевого сплава, содержащего добавку редкоземельного (0,2% Nd) материала, при комнатной температуре со скоростями деформации 3,3·10–5, 1,1·10–4, 1,1·10–3, 3,3·10–3 и 1,1·10–2 с–1 приведено в [54]. В работе отмечается отличие прерывистой пластичности, связанной с полосами Людерса и эффектом Портевена–Ле Шателье, как по кинематическим характеристикам (геометрические размеры, скорость движения), так и по механизмам. В материалах с гексагональной решеткой значительный вклад (около 50 %) в деформацию, обусловленную полосами Людерса, вносится двойниками, причем последние при подходе к границам зерен могут генерировать двойники в соседних зернах. Эффект Портевена–Ле Шателье связан с дислокационным механизмом деформирования и торможением дислокаций диффундирующими к ним примесями.

В работе [13] высказывается предположение, что эффект ПЛШ может являться макроскопическим проявлением неустойчивости неупругого деформирования по различным механизмам на микро- и мезоуровнях, возникающей в разных диапазонах параметров воздействий. Это могут быть и отрывы дислокаций от атмосфер Коттрелла, и зернограничные сдвиги, и возникновение мезополос и кооперативных полос сдвига, и разрушение-восстановление частиц жестких включений, и резкие перестройки дислокационных субструктур. Каждое из этих явлений имеет подтверждение и в экспериментальных исследованиях на мезо- и микроуровнях, и при моделировании с использованием моделей различных масштабных уровней.

Модели для описания эффекта Портевена–Ле Шателье

Пластическая (более широко – неупругая) деформация любых материалов и в любых диапазонах воздействий может трактоваться как совокупность огромного количества актов резкого изменения параметров различной природы и размерности – от точечных дефектов до конгломератов зерен. Иначе говоря, неупругую деформацию можно рассматривать как череду разномасштабных неустойчивостей. Когда эти неустойчивые процессы реализуются на микромасштабах («перескоки» дислокаций в энергетическом рельефе Пайерлса, прорывы скоплений дислокаций через барьеры различной природы и т.д.), то на макро- и даже на мезомасштабах они наблюдаются как монотонные, гладкие изменения конфигурации тела, поскольку реализуются эти неустойчивые процессы большими совокупностями физических носителей неупругой деформации неупорядоченно, несогласованно ни во времени, ни в пространстве. Однако, если движение различных носителей или их групп начинает осуществляться согласованно, самоорганизованно, неустойчивый характер деформирования становится наблюдаемым на мезо- и макроуровне. Это проявляется на диаграммах «отклик – воздействие» в виде немонотонных кривых зависимости отклика при монотонно изменяющихся воздействиях, и в таких случаях говорят о «прерывистой», «пилообразной» или «зазубренной» (serrated) пластической деформации.

Процесс развития пластической деформации в настоящее время рассматривают на различных масштабных (структурных) уровнях: микро-, мезо- и макроуровне. Исследование «тонкостей» процессов эволюции дислокационных субструктур и точечных дефектов, особенно – во внутренних областях образцов, с помощью экспериментальных методов связано с огромными принципиальными сложностями и высокими затратами. В связи с этим обстоятельством в последние 20 лет интенсивно развиваются математические модели различных масштабных уровней.

Математические модели позволяют исследовать явление пластичности кристаллов, включая условия возникновения деформационных дефектов, их движение, взаимодействие, аннигиляцию, которые трудно или невозможно наблюдать в реальном физическом эксперименте.

Макрофеноменологические модели

Одна из известных феноменологических моделей, ориентированная на описание эффекта ПЛШ при одноосном нагружении, предложена в [44]. Скоростная чувствительность материала определяется суммой двух составляющих: не зависящей и зависящей от деформационного старения; последняя устанавливается с применением дислокационной подмодели, включающей в себя два эволюционных уравнения (обыкновенные дифференциальные уравнения первого порядка) для скалярных плотностей мобильных и лесовых (иммобильных) дислокаций. Область реализации режима прерывистой пластичности соответствует отрицательной скоростной чувствительности, границы этой области определяются по нулевой скоростной чувствительности. Отмечается, что модель позволяет определить критические значения накопленных деформаций (начала и завершения прерывистой пластичности), действительно наблюдаемые в экспериментах.

В работе [53] с диффузионным старением связывается два вида неустойчивости пластического течения: распространение полос Людерса и эффект Портевена–Ле Шателье (ПЛШ), основное внимание уделено описанию эффекта ПЛШ. Движение дислокаций рассматривается как процесс весьма быстрого свободного движения и длительной остановки на препятствиях различной природы. При остановках на препятствиях к ядрам и в окрестности дислокаций стекаются атомы примесей, образующие «облака» (атмосферы) атомов, взаимодействующие с дислокациями и затрудняющие их движение. При дальнейшем повышении напряжений происходит отрыв дислокаций и их движение до следующего препятствия; при этом полагается, что дислокации не «тянут» за собой атмосферы. Последнее предположение не представляется достаточно обоснованным, более правдоподобной представляется гипотеза об увлечении за собой части атомов атмосфер движущимися дислокациями, в результате чего должно повышаться вязкое сопротивление движению дислокаций, окруженных примесными атомами. Приведен краткий обзор работ, посвященных экспериментальным и теоретическим исследованиям эффекта ПЛШ.

В качестве базисного уравнения использована модификация модели, предложенной в 1988 г. Мак-Кормиком:

-A G

Ё = Ё 0 e к6 , где е - скорость деформации; AG - свободная энергия Гиббса; к - постоянная Больцмана; 0 - абсолютная температура; е0 - так называемая отсчетная скорость деформации (равная скорости сдвига при нулевой свободной энергии Гиббса). Полагается, что AG является функцией эффективного напряжения (разности действующего напряжения и предела текучести при 0 К) и концентрации примеси. Концентрация примеси определена функцией времени задержки дислокаций на препятствиях, отнесенного к характерному времени диффузии; приведено феноменологическое соотношение для определения времени задержки, предложенное ранее другими исследователями. В конечном счете получено определяющее соотношение (зависимость напряжения от скорости деформаций и температуры) для одноосного нагружения. Отмечается, что при квазистатическом режиме деформирования скоростная чувствительность материала согласно модели оказывается отрицательной, а следовательно, деформирование – неустойчивым. Ряд авторов связывают возникновение режима знакопеременной скоростной чувствительности с динамическими процессами. При этом возможно изменение знака скоростной чувствительности и переход к «зубчатому» характеру отклика. Для многоосного напряженно-деформированного состояния (НДС) определяющее соотношение обобщается обычно используемым приемом – заменой одноосных мер напряжений и скорости деформации на соответствующие девиаторы.

Большая часть статьи посвящена исследованию устойчивости деформирования системы, включающей деформируемый образец и нагружающее устройство, рассматриваемое как упругий стержень. Для анализа используется аппарат линейной теории возмущений. Получены условия устойчивости для пространственных и временных возмущений; показано существенное влияние на устойчивость деформирования и характер неустойчивого поведения жесткости нагружающего устройства и характеристик упрочнения материала. Отмечается, что предложенная модель материала позволяет описать и «зуб текучести», и эффект ПЛШ.

Другой механизм прерывистой пластичности, названной авторами псевдоПЛШ-эффектом, наблюдаемый в упорядоченных твердых растворах, рассматривается в [26]. При термомеханических воздействиях в процессе неупругого деформирования имеет место уменьшение упорядоченности, которая может восстанавливаться за счет диффузионных механизмов. Рассматривается конститутивная модель для случая одноосного нагружения. Предложено кинетическое уравнение для параметра порядка, изменяющегося в пределах от 0 (полностью неупорядоченный) до 1 (полностью упорядоченный твердый раствор). В качестве определяющего соотношения использовано уравнение нелинейно-вязкой жидкости со степенной зависимостью напряжений от скорости деформации, в котором напряжение течения зависит от параметра порядка. Получено аналитическое решение системы уравнений конститутивной модели, анализ которого позволил определить наличие пределов по температуре и скорости деформации, в которых может реализовываться режим прерывистой текучести.

В [46] приведены результаты статистического анализа кривых напряжение – деформация для одноосного нагружения монокристаллических образцов из сплава Al-4,5% Mg. Эксперименты проведены для двух ориентировок кристаллита относительно оси растяжения (<111> и <100>) при температурах 300, 350 и 400 К и скоростях деформирования в диапазоне (3,2·10–6–1,3·10–3) с–1. Для описания эффекта ПЛШ использована одноосная модель деформирования, в которой напряжение течения определяется суммой членов, зависящих от накопленной деформации и от текущей скорости деформации (оба члена зависят и от температуры), причем зависимость напряжения от скорости деформации (2-й член в аддитивном представлении) имеет N-образный вид. Для введения в рассмотрение пространственной неоднородности деформаций, отражающей наблюдаемое в экспериментах образование и распространение полос скольжения, предлагается простая стержневая модель, согласно которой одномерный образец представляется совокупностью конечного числа слоев. В каждом элементарном стержне (слое) напряжение течения, помимо двух указанных выше составляющих, содержит добавочный аддитивный член, который зависит от разностей напряжений в рассматриваемом слое и двух соседних. Показано, что рассматриваемая модель позволяет качественно описать пространственно-временное распределение локализации деформаций и эффект ПЛШ.

Стохастическая модель для описания на мезо- и макроуровне эффекта ПЛШ предложена в статье [35]; указанный эффект объясняется коллективным взаимодействием дислокаций дальнодействующими полями напряжений. Получено стохастическое дифференциальное уравнение (типа Фоккера–Планка–Колмогорова), описывающее эволюции функции распределения вероятности отклонения локальной деформации от средней на заданную величину. Модель использована для описания поведения монокристаллического образца, деформируемого одиночным сдвигом; сопоставление теоретических и экспериментальных результатов демонстрирует удовлетворительное соответствие.

Краткий обзор работ, в которых предлагаются различные механизмы, обусловливающие эффект ПЛШ, и модели для их описания, содержится в [34]. Автором предлагается модель для случая одноосного нагружения, позволяющая качественно воспроизводить режим прерывистой пластичности. Для этого в эволюционное уравнение для напряжения течения вводится дополнительный член с внутренней переменной, отвечающей за процесс динамического старения. Проведен тщательный анализ линейной устойчивости конститутивной модели материала, получены оценки границ устойчивого (монотонного) отклика и области прерывистой пластичности в пространстве параметров состояния материала (температуры, скорости деформации и деформации).

В [82] для описания эффекта ПЛШ использована макрофеноме-нологическая вязкоупругая модель в сочетании с методом конечных элементов (МКЭ) в 3-мерной постановке. Соотношение для скорости неупругих деформаций включает зависимость от концентрации примесей; предложено также феноменологическое уравнение для концентрации примесей, зависящей от накопленной неупругой деформации и времени старения. Численные эксперименты проведены для образцов прямоугольного и круглого поперечного сечения (сплав Al–Mg–Si), подвергаемых растяжению с постоянной скоростью деформации. В качестве начального возмущения вводилось отклонение или в одном конечном элементе, или с помощью случайно распределенных по всему объему отклонений в пределах 0–10 МПа. Показано, что модель позволяет качественно описать эффект ПЛШ, реализуемый за счет образования и перемещения вдоль оси образца шейки.

Аналогичная модель использована в [32] для анализа деформирования сплавов Al–Li и Al–Cu. Для численного исследования примене- ны образцы прямоугольного сечения с плоскими гранями, с V-образными надрезами (с углами 60 и 90°) и с плоскими надрезами, моделирующими трещины. Детально проанализировано зарождение и распространение полос сдвига, влияние на их кинетику изменения формы надреза и деформационного старения.

В [27] описано применение метода клеточных автоматов в двумерной постановке для анализа эффекта ПЛШ. Рассматривается движение дислокаций в поле случайно распределенных барьеров, на которых дислокации могут временно задерживаться. Во время задержки к заторможенным дислокациям стекаются атомы примесей, что увеличивает необходимую энергию активации для дальнейшего движения. Активация задержанных дислокаций происходит под действием приложенных напряжений, сил дальнодействующего взаимодействия и случайных флуктуаций температуры. Показано, что эффект ПЛШ может быть описан только при одновременном учете дальнодействующих сил между дислокациями и динамического деформационного старения.

Обширный перечень работ, посвященных экспериментальным исследованиям и теоретическим моделям эффекта ПЛШ, приведен в [62]. Основным механизмом, как и в большинстве других работ, считается закрепление дислокаций атомами примесей во время задержек движения дислокаций барьерами различной природы; отмечается, что эффект ПЛШ следует отличать от других видов неустойчивости пластической деформации (например, полос Людерса), в первую очередь – повторяемостью, в определенном смысле – «возобновляемостью» механизмов и движущих сил эффекта ПЛШ. Анализ существующих моделей обнаруживает ряд их существенных недостатков, в частности невозможность определить с их помощью основные параметры неустойчивого деформирования (ширину, скорость распространения и величину деформации в полосах локализации), сложность использования в рамках континуальных моделей.

Отличительной чертой предлагаемой модели авторы считают введение двух характерных масштабов времени, один из которых связан с динамическим деформационным старением, а второй – с мобильностью дислокаций. В качестве базовой используется модель МакКормика, согласно которой скорость пластической деформации определяется законом аррениусовского типа, т.е. экспоненциальным законом энергии активации движения дислокаций, температуры процесса, текущей скоростной чувствительности материала и эффективного напряжения, равного разности приложенных и внутренних напряжений. Внутренние напряжения связываются с деформационным упрочнением и полагаются линейно зависящими от пластических деформаций. В энергию активации вводится дополнительный аддитивный член, пропорциональный концентрации примесных атомов, осаждающихся на дислокациях. Предложено эволюционное уравнение для описания изменения данной «добавки» в энергию активации, представляющее собой обыкновенное дифференциальное уравнение (ОДУ). Осуществлен детальный качественный анализ эволюционного уравнения (стационарный режим, бифуркации, особые точки и т.д.). В дальнейшем это эволюционное уравнение дополняется диффузионным членом. Собственно определяющее соотношение расширяется включением в него члена, описывающего поведение нагружающего устройства. Проведен качественный анализ полученной системы двух дифференциальных уравнений (одно – ОДУ, второе – дифференциальное уравнение в частных производных (ДУЧП)), осуществленный с помощью численной процедуры. Показано, что предложенная одномерная и по существу макрофеноменологическая модель качественно удовлетворительно описывает эффект ПЛШ.

Для анализа движения дислокаций и их взаимодействия с примесными атомами в [37] используется модель фазового поля, в которую введены уравнения диффузии примеси. Разрешающие уравнения модели получены на основе термодинамического подхода, предложены соотношения для упругой, химической и дислокационной составляющих свободной энергии. Рассмотрено взаимодействие примесных атомов с источником Франка–Рида, неподвижными и движущимися дислокациями. Показано, что модель качественно корректно описывает как дальнодействующие взаимодействия (полями напряжений дислокаций), так и взаимодействия ближнего порядка (с атомами примесей).

Детальный обзор методов и результатов исследования неустойчивости пластической деформации (включая «зуб текучести» и прерывистую пластичность) приведен в [4, 5]. Выделяется низкотемпературная (при температурах жидкого водорода, гелия или азота) и высокотемпературная (при 0,3–0,7 гомологической температуре) прерывистая пластичность. Низкотемпературная прерывистая текучесть связывается с процессами двойникования и фазовыми превращениями; отмечается существенное влияние на процесс размеров и состояния поверхности образцов. Высокотемпературная прерывистая пластичность обусловлена локализацией деформации с образованием полос сдвига; на основании анализа результатов одноосного растяжения образцов из разных материалов отмечается различный характер образования и эволюции полос сдвига при постоянной скорости изменения напряжения или деформации. На основе анализа известных экспериментальных данных сделаны выводы об общих закономерностях прерывистой пластичности; особо подчеркивается, что данный эффект определяется процессами мезоуровня, а не микроуровня [4]. Во второй части обзора [5] содержится детальный анализ теоретических положений и моделей, предлагаемых для описания прерывистой текучести; основным недостатком рассмотренных работ автор считает отсутствие в большинстве из них анализа процессов, происходящих на более высоких, чем микроуровень, масштабных уровнях.

Результаты экспериментальных исследований прерывистой пластичности гладких и надрезанных цилиндрических, призматических и плоских образцов из алюминиевого сплава, подвергаемых одноосному нагружению при комнатной температуре в интервале скоростей деформации от 10–5 до 103 с–1, представлены в [21, 22]. Макрофеномено-логическая упруговязкопластическая модель, опирающаяся на экспериментальные данные при одноосном нагружении, рассмотрена в [21]. Согласно модели напряжение течения полагается суммой предела текучести, величины возросшего за счет пластического упрочнения сопротивления и слагаемого, зависящего от скорости неупругой деформации («вязкое сопротивление»). Принимается, что последнее слагаемое в определенном диапазоне скоростей деформаций может иметь отрицательную производную («отрицательную скоростную чувствительность»). Проведен качественный анализ модели для случая одноосного нагружения. Значительное внимание уделено анализу устойчивости неупругого деформирования, для чего использован метод малых возмущений. Рассматриваемая модель обобщена на случай трехмерного напряженно-деформированного состояния (НДС) и применена в конечно-элементном пакете LS-DYNA для исследования деформирования цилиндрических образцов (гладких и с кольцевой выточкой с различными радиусами скругления) из алюминиевого сплава 5083-H116. Приведены и анализируются особенности эволюции НДС для образцов различной конфигурации и при разных скоростях деформирования; результаты свидетельствуют о реализации прерывистой пластичности в широком диапазоне скоростей деформации. Исследуется влияние на результаты расчетов размеров конечно-элементной сетки и шага интегрирования по времени. Вплотную к рассмотренной выше примыкает статья [22], в которой содержатся результаты тщательно выполненных и обработанных экспериментальных исследований на одноосное нагружение образцов круглого и прямоугольного поперечного сечения.

Макрофеноменологическая модель для анализа прерывистой пластичности предложена в [76]. Рассмотрено одноосное нагружение по-ликристаллического образца в условиях плоско-напряженного и плоско-деформированного состояния. Предполагается, что неупругое деформирование реализуется сдвигом по одной и/или двум системам скольжения. Скорость сдвига на каждой системе скольжения определяется вязкопластическим законом степенного типа, включающим также зависимость от концентрации примесей на этой системе. Для определения концентрации примесей на системе скольжения предложено эволюционное соотношение, согласно которому концентрация возрастает с ростом накопленного сдвига и уменьшением скорости сдвига по этой системе. Для определения положения полос сдвига используется линейный бифуркационный подход. Отмечается удовлетворительное соответствие результатов расчета данным экспериментальных исследований.

В [23] для описания эффекта ПЛШ использована геометрически нелинейная макрофеноменологическая упруговязкопластическая модель в сочетании с методом конечных элементов в 3-мерной постановке. В основу конститутивной модели положен неогуковский закон, в качестве меры упругой деформации принят тензор деформаций Альманси, определяемый по упругой составляющей градиента места. Скорость неупругих деформаций определяется соотношениями теории пластического течения, напряжение течения в которых зависит от концентрации примесных атомов; последняя определяется феноменологическим эволюционным уравнением (функцией накопленной пластической деформации и времени старения). Значения материальных параметров были экспериментально определены на основе испытаний на растяжение. Поликристаллические плоские образцы размерами 5,1×1,5×21 мм были изготовлены из сплава Al-Mg (AA5754). Все об- разцы были вырезаны из листовых материалов с осью растяжения в направлении прокатки. После шлифовки и полировки образцы были подвергнуты отжигу (выдержка в течение 2 часов при температуре 400 °С) и закалке в воде. Испытания на растяжение проводились при комнатной температуре, при постоянных скоростях деформации от 2·10–5 до 6·10–3 с–1. Сопоставление теоретических результатов с данными проведенных авторами экспериментов обнаруживает удовлетворительное соответствие.

Результаты экспериментальных и теоретических исследований одноосного нагружения образцов (алюминиевый сплав Al 4% Cu (A2017)) представлены в [38]. Основной целью работы является изучение пространственно-временных особенностей трех типов (полос А, В и С) проявления эффекта ПЛШ. Приведено краткое описание методики эксперимента. С целью уменьшения остаточных напряжений образцы были подвергнуты отжигу (выдержка в течение 4 часов при температуре 723 К и медленное охлаждение в печи). Средний размер зерен образца был определен с помощью оптического микроскопа и составил 30 мкм. Все испытания проведены на одноосное растяжение при постоянных скоростях деформации в диапазоне 10–5–5·10–3 с–1. Показано, что при снижении скорости деформации наблюдается изменение типа полос сдвига А → В → С.

Для теоретического описания эффекта ПЛШ используется мак-рофеноменологическая одномерная вязкопластическая модель, учитывающая влияние на скорость деформации концентрации примесей; предложено эволюционное уравнение для определения изменения последней. Приведено описание разностной схемы для анализа деформирования стержня, в которой учитывается жесткость нагружающей системы. Сопоставление теоретических и экспериментальных результатов для трех типов кривых демонстрирует удовлетворительное соответствие.

Результаты экспериментальных и теоретических исследований одноосного нагружения образцов (алюминиевый сплав 2024), вырезанных из листовых катаных заготовок под углами 0, 45 и 90° к направлению прокатки, представлены в [25]. Все испытания проведены при комнатной температуре, скорости деформации от 1·10–5 до 7·10–1 с–1. В диапазоне малых скоростей деформации (1·10–4–1·10–3) с–1 наблюдается «реверсивное» скоростное упрочнение (снижение напряжения течения с ростом скорости деформации), сопровождаемое пре- рывистым режимом течения. При скоростях деформации, превышающих 1·10–2 с–1, напряжение течения возрастает с увеличением скорости деформации, и деформирование реализуется монотонно. Для теоретического описания процесса деформирования применяется макрофено-менологическая теория упруговязкопластичности, в которой принимается аддитивное разложение скорости деформации на упругую, пластическую и вязкую составляющие. Напряжение течения представляется суммой составляющих, зависящих от накопленной пластической деформации, скорости деформации и процесса деформационного старения. Предложено обобщение геометрически линейных определяющих соотношений на случай больших градиентов перемещений. Значительное внимание уделено статистическому анализу теоретических и экспериментальных данных, на основе которого установлены условия перехода от нелинейного хаотического режима (полосы типа С) к режиму «самоорганизованной критичности» (полосы типа А).

Модификации макрофеноменологической модели, предложенной ранее (2001 г.) первым из авторов указанной ниже статьи (совместно с J.R. Klepazcko), позволяющие описывать эффекты динамического деформационного старения (отрицательную скоростную чувствительность материала), приведены в [63]. Модификации модели ориентированы на описание поведения алюминиевых сплавов (с магнием, марганцем, кремнием, цинком и другими компонентами) в широких диапазонах скоростей деформации 10–4–104 с–1 и температур 223–500 К. Определяющие соотношения формулируются для случая одноосного нагружения, напряжения течения в предлагаемых соотношениях полагают равными сумме составляющих, отвечающих за деформационное упрочнение, вязкое сопротивление и снижение сопротивления деформации в определенном диапазоне скоростей деформаций, каждая из составляющих зависит от температуры. Приведены эволюционные уравнения для материальных параметров, входящих в соотношения. Показано удовлетворительное соответствие результатов моделирования экспериментальным данным как в области отрицательной скоростной чувствительности (скорости деформации 10–4–102 с–1), так и переход к положительной скоростной чувствительности при более высоких скоростях деформации. В статье не рассматривается применение предлагаемых соотношений для описания эффекта ПЛШ, однако они пригодны для такого анализа.

Результаты численного анализа плоских и цилиндрических, гладких и с надрезами образцов из никелевого суперсплава, подвергаемых одноосному растяжению при температуре 500 °С и скоростях деформации 10–6–10–2 с–1, приведены в [50]. Для описания деформационного старения использована модель Мак-Кормика. Реализация модели осуществлена методом конечных элементов в двух- и трехмерной постановках. Показано, что при низких скоростях деформирования (порядка 10–6 с–1) неустойчивость пластического течения соответствует формированию полос типа С, в промежуточной области (порядка 10–4 с–1) – типа В, а при относительно высоких скоростях деформирования (порядка 10–2 с–1) – типа А. Значительное внимание уделяется процедуре интегрирования (по времени) конститутивных уравнений, предлагается алгоритм, существенно снижающий затраты машинного времени при сохранении устойчивости и точности. Тщательно исследовано влияние на результаты расчетов используемых сеток.

В [48] на основе физического анализа скоростного упрочнения полагается, что зависимость напряжения течения от скорости деформации можно представить в виде двух составляющих: вклада от вязкого сопротивления движению дислокаций и через зависимость деформационного упрочнения за счет скоплений иммобильных дислокаций. При низких скоростях деформации и повышенной температуре к скоплениям дислокаций «стекаются» примесные атомы, закрепляя эти дислокационные барьеры; повышение скорости деформации способствует активизации части иммобильных дислокаций и уменьшает приток примесных атомов к скоплениям дислокаций. Указанные механизмы делают деформационное упрочнение чувствительным к скорости деформации и температуре, приводит к возникновению диапазонов этих параметров, в которых возникает отрицательная скоростная чувствительность и прерывистый режим деформирования. Отмечается, что учет этих механизмов позволяет объяснить экспериментально наблюдаемый факт возникновения прерывистой пластичности только после достижения некоторой критической накопленной пластической деформации. С использованием предложенной модели на основе линейного анализа устойчивости предложен критерий, устанавливающий момент проявления эффекта Портевена–Ле Шателье для одноосного нагружения в зависимости от накопленной пластической деформации, температуры и скорости деформации.

Макрофеноменологическая модель, представляющая собой модификацию модели Мак-Кормика и ориентированная на описание поведения метастабильной нержавеющей стали аустенитного класса, рассмотрена в [45]. В уравнении поверхности текучести напряжение течения зависит от членов, отвечающих за динамическое и статическое деформационное старение, мартенситное превращение части материала и скоростное упрочнение-разупрочнение. Значительное внимание уделяется процедуре идентификации, для чего используются результаты собственных экспериментов авторов; приведено краткое описание методики экспериментов и полученных результатов. Проведены испытания при постоянных и ступенчато изменяющихся скоростях деформации, с разгрузкой и выдержкой (от 3 до 56 дней) между двумя этапами монотонного деформирования. Отмечается качественное соответствие теоретических результатов экспериментальным данным.

Как уже отмечалось выше, в ряде работ по исследованию эффекта ПЛШ проявление последнего связывается с возникновением полос сдвига. Поскольку полоса сдвига представляется собой область локализованных деформаций, естественны попытки применения для их описания градиентных теорий пластичности. В [79] рассматривается упрощенная жесткопластическая градиентная модель, в которой в закон упрочнения введен дополнительный член, пропорциональный второму градиенту от интенсивности накопленной пластической деформации. Исследованы варианты с независимой и зависимой от скорости деформации пластичностью. Для тестовой задачи простого сдвига рассмотрены особенности возникновения и эволюции полос сдвига. Физические причины возможных флуктуаций напряжения текучести и связи их с диффузией примесных атомов в работе не анализируются.

Градиентная упругопластическая модель, в которой введены вторые градиенты вектора перемещений и сопряженные с ними моментные напряжения, представлена в [66]. Рассмотрены результаты применения модели для исследования локализации пластических деформаций (образования полос сдвига); в качестве примера использована задача чистого сдвига. Напряжение течения полагается зависящим от инвариантов тензора малых деформаций и тензора 3-го ранга – меры деформации, порождаемой вторыми градиентами вектора перемещений. Сопротивление деформации аппроксимировано кусочно-линейной функцией меры деформации, содержащей участок разупрочнения.

Хотя напрямую данная модель не ориентирована на описание эффекта ПЛШ, представляется возможным использовать ее с этой целью, для чего необходимо в диаграмму «напряжение – деформация» ввести зависимость от скорости деформации и температуры, что можно осуществить с помощью параметрической зависимости коэффициентов в аппроксимации кривой, определяющей напряжение текучести как функцию параметров процесса.

В [51] для исследования полос Людерса и прерывистой пластичности предлагается использовать простой вариант макрофеноменоло-гической градиентной теории, в которой в качестве дополнительной внутренней переменной вводится градиент интенсивности накопленной пластической деформации. На примере численного решения плоских задач растяжения полосы (с различной толщиной) показано, что результаты, полученные с помощью классической теории пластического течения, существенно зависят от аппроксимации области конечными элементами; предлагаемая модель позволяет исключить подобную зависимость.

Заключение

Предлагается краткий обзор работ, посвященных описанию физических механизмов и результатов экспериментальных исследований особенностей деформирования сплавов в температурно-скоростных диапазонах, в которых существенное влияние на поведение материалов оказывают диффузионные процессы. Особое внимание уделено рассмотрению прерывистой пластичности, возникновение которой большинство авторов связывают с образованием полос сдвига и взаимодействием дислокаций с атмосферами примесных атомов; приведенные в цитируемых работах экспериментальные данные подтверждают правомерность этой точки зрения. Следует отметить, что исследование «тонкостей» процессов эволюции дислокационных субструктур и точечных дефектов, особенно во внутренних областях образцов, с помощью экспериментальных методов связано с огромными принципиальными сложностями и высокими затратами. В связи с этим обстоятельством в последние десятилетия интенсивно развиваются математические модели различных масштабных уровней. Следует отметить, что математические модели не могут полностью заменить экспериментальные исследования, последние необходимо развивать и совершенствовать, поскольку без новых эмпирических данных едва ли возможно создание новых углубленных моделей, обладающих высоким прогнозным потенциалом. В настоящей работе авторы ограничились рассмотрением только наиболее известных макрофеноменологических моделей, поэтому данный обзор не претендует на полноту. Следует отметить, что указанный класс моделей основан на экспериментальных исследованиях, в силу чего макрофеноменологические модели не обладают универсальностью и не могут быть использованы для предсказания свойств проектируемых материалов. В значительной мере в рассмотренных моделях правильно понимаемая физика процессов «напрямую» вводится в определяющие соотношения, без использования параметров, описывающих указанные механизмы и их носителей. В статье не рассматривались подходы, основанные на физических теориях пластичности и многоуровневых моделях, представляющие предмет следующей публикации. По мнению авторов, многоуровневые модели лишены многих из отмеченных выше недостатков.

Работа выполнена в Пермском национальном исследовательском политехническом университете при финансовой поддержке Минобрнауки РФ (базовая часть государственного задания ПНИПУ, № гос. регистр. 01201460535) и РФФИ (проекты №№13-01-96006 р_урал_а, 14-01-00069-а).