При решения тригонометрических уравнения отбор корней

Самое важное отличие тригонометрических выражений от алгебраических состоит в том, что в алгебраических выражениях конечное число корней, а в тригонометрических - бесконечное, что сильно усложняет отбор корней. Еще одной спецификой тригонометрических выражений является неединственность формы записи ответа.

Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений весьма специфична и обычно оказывается более сложной, чем это имело место для уравнений алгебраических. Приведем решения уравнений, иллюстрирующие типичные случаи появления посторонних корней и методы борьбы с ними.

Пример 1. Найти ближайший к числу-- корень уравнения

sin x cos 2 x + sin x +   sin 2 x = cos x +

Решение.

sin x I 2cos² x

- 1 + 1 + cos x

3 (       10 ^

I cos x + I ^

4 1        11 J

.   „     f       10 ^   3 (       10 ^

sin x2 cos x I cos x + I - I cos x + I = 0 ^

I        11 J 4 1        11 J

= 0 ^

. 10 If , cos x + |I sin 2 x —

11 Л cos x + — = 0

., 13 Л sin 2 x — = 0

x = ±1 n - arccos I + 2nk

I

Г •3

arcsin — + 2nm

2 x =

n - arcsin   + 2nm

Подставляя последовательно в формулу

r =

13n x--

вместо переменной

x выписанные выше серии решений уравнений, отыщем для каждой из них min r , а затем сравним полученные минимальные r между собой.

a) r ₁

13 n

n - arccos — + 2 n ( k - 1)

Ясно, что min r

n       10

достигается при k = 1 , то есть min r = — + arccos — .

б) r ₂ = x ₂

—

13n

- n + arccos-- + 2nk - 3 n -

П

n .         10 . „  „

---+ arccos-- + 2 n ( k - 2)

4         11

min r =

n       10

--arccos — .

4         11

в) r ₃

г) r ₄ =

13 n

— arcsin 334 + nm - 3 n-- 24

arcsin 34 2

— arcsin —

13n x4   4

n 1      .  3 .       „ n

---arcsin — + nm - 3 n--

22   4      4

n 1     ■  3

---arcsin — + n ( m - 3) 42   4

n 1.3

min r =---arcsin — .

Выберем минимальное из чисел r , i = 1,4. Сразу ясно, что minr  arcsin ^

4       11   4  2      4          11  24

^ 2 arccos — > arcsin — ^

10           103

(**)

2sinarccos • cosarccos >sinarcsin ^

11           114

—

2(       10) 10  3   „ У21 103

cos21 arccos — I — > — ^ 2> —

I       11) 11   4       11   114

^ 80^21 >3 - 12| ^ 6400 • 21> 9 - 1 21² ^ 44800 > 43923.

Последнее неравенство - верное, а все сделанные переходы -равносильные. Поэтому верно исходное неравенство. Обоснуем равносильность переходов (*) и (**) (равносильность остальных переходов следует из общих свойств числовых неравнств). В случае преобраования (*),

10     1       3

достаточно заметить, что числа arccos и arcsin расположен на участке

(0; ^п ) монотонного возрастания функции sin x . В случае перехода (**)

формула sin а = 71 — _cos ² а справедлива, так как а = arccos 10 е (0; ^п ) .

Ответ. x = 3 п + arccos — .

Пример 2. Найти корни уравнения: Vcos 2 x + sin3 x = 42 cos x .

Решение этого уравнения распадается на два этапа: 1) решение уравнения, получающегося из данного возведением в квадрат обеих его частей; 2) отбор тех корней, которые удовлетворяют условию cosx> 0 . При этом заботится об условии cos 2 x+sin3 x < 0 нет необходимости. Все значения k , удовлетворяющие возведенному в квадрат уравнению, этому условию удовлетворяют.

Первый шаг нас приводит к уравнению sin3 x = 1 , откуда x = ^п + —k .

Теперь надо определить, при каких k будет cos(n + 2^ k) > 0. Для этого достаточно для k рассмотреть значения 0 , 1, 2 , т. е. <<обойти один раз круг>>, поскольку дальше значения косинуса начнут повторяться, получившиеся углы будут отличаться от уже рассмотренных на величину, кратную 2п.

Ответ. x = ^П + 2 П , — + 2 П .

Итак, основная схема отбора корней состоит в следующем. Находится наименьший общий период всех тригонометрических функций входящих в уравнение. На этом периоде отбираются корни, а затем оставшиеся корни периодически продолжаются.

Пример 3. Решить уравнение: | cos x |= sin x + 1.

Решение. Уравнение равносильно смешанной системе:

2 I                     ¹ I

| cos x | = I Sin x + I ,

I      2 J sin x + — > 0

^<

3 2sin2 x + sin x — = 0, sin x > —

.    -2 ± 74 + 83"   - 1 -± 77

sin x =              =

_TT -1 - 77     1

Но------<-----не годится.

Ответ. x = ( - 1) k arcsin

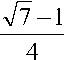
+ nk .

Раскрывая знак модуля получаем более громоздное решение. А ответ в этом случае принимает вид:

Ответ. x =-- + arcsin-- + 2 n .

Литературы:

• 1.    А.И.Яблонский. Электронный учебник по высшей математике. М., 1993 г.

• 2.    Ё.Юсупов. Математика. Учебное пособие. ФФ ТУИТ, 2009 г.

• 3.    П.Е.Данко и др. Математика в упражнениях и задачах 2-х частях. М., 2006 г.

"Экономика и социум" №4(83) 2021