Приближение оценки QN параметра масштаба с помощью быстрых М-оценок

Один из подходов к оптимизации и принятию решений в условиях неопределенности вероятностных моделей сигналов и помех связан с использованием робастных статистических методов, обеспечивающих устойчивость и надежность результатов статистического анализа к возможным отклонениям от принятых гипотез о распределениях [1]. В свою очередь задачи робастного оценивания параметра масштаба распределений занимают второе по значению место после задач робастного оценивания параметра положения распределений [2]. В данной статье предлагаются быстрые высокоэффективные и робастные оценки параметра масштаба симметричных распределений.

Оценкой масштаба называется любая положительная статистика S n , которая удовлетворяет равенству S n ( ax 1 , …, ax n ) = aS n ( x 1 , …, x n ) для a > 0 [2–4]. Такая оценка определяет степень разброса значений в выборке и может использоваться как в непараметрических задачах, так и для оценивания значений неизвестного параметра масштаба семейства распределений вероятности. Примером такого параметра может служить параметр σ нормального распределения с плотностью вероятности N (0, σ ²) = exp(– x ²/2 σ ) / (2 πσ ²)^1/2, а возможной оценкой – стандартное отклонение SD .

Эта часто используемая оценка обладает серьезным недостатком: при небольших отклонениях от предполагаемой модели результат может оказаться далеким от истинного. Такими отклонениями могут быть загрязненные данные или ошибочные предположения о законе распределения генеральной совокупности. Классическая статистика рассматривает идеализированные условия, но, согласно [3], в статистических данных, как правило, встречается от 1 до 10 % больших ошибок, а некоторые ряды измерения после тщательной проверки не подтверждают принадлежность нормальному распределению, имея более тяжелые «хвосты».

Подобные отклонения от идеальной модели рассматриваются в робастной статистике. В зависимости от задачи в качестве робастных альтернатив для оценивания масштаба чаще всего используют межквартильный размах IQR = F–1(3/4) – F–1(1/4) или абсолютное медианное отклонение от медианы MAD = medi | xi – med x |. Одним из критериев робастности в данном случае служит пороговая точка оценки, т. е. наибольший процент наблюдений, который можно заменить произвольно большими значениями, оказав лишь ограниченное влияние на значение самой оценки [2]. По этому критерию абсолютное медианное отклонение является более предпочтительным, поскольку оно имеет максимально возможную пороговую точку 50 %. Пороговые точки стандартного отклонения и межквартильного размаха равны 0 и 25 % соответственно.

Стандартное отклонение SD имеет минимальную возможную дисперсию для нормального распределения. Робастные же оценки обладают более высокой пороговой точкой, как правило за счет большей дисперсии, т. е. меньшей точности. В этом случае эффективность оценки MAD равна всего 36,7 %, поэтому возникает необходимость построения более эффективных оценок с максимальной пороговой точкой.

В работе [5] были предложены такие оценки, одна из которых, а именно Q n , впоследствии стала часто использоваться на практике. Оценка Q определяется как первый квартиль расстояний между наблюдениями: Q = {| x_i – x j |} ( _k ) , k = C ( h , 2), h = [ n /2] + 1, и имеет асимптотическую эффективность 82,3 % и пороговую точку 50 %. Серьезным недостатком является большая вычислительная сложность такой оценки, так как задействовано n ² разностей между парами значений. Отметим, что даже более эффективный алгоритм [6] требует в 3–5 раз больше времени, чем MAD .

В данной статье используется параметрическое семейство оценок масштаба, имеющих такую же или большую эффективность за счет снижения пороговой точки, которая, тем не менее, остается в разумных пределах. Введенный параметр позволяет сохранить баланс между пороговой точкой и эффективностью в зависимости от решаемой задачи.

Постановка задачи. В теории робастности важным инструментом для анализа оценок является подход на основе функции влияния. Функция влияния IF ( x ; S , F ) оценки S на модельном распределении F показывает устойчивость оценки к большим ошибкам в точке x и определяется как ее производная по Гато [3]. Построим оценку масштаба с функцией влияния, совпадающей с IF ( x ; Q , F ), тем самым обеспечив совпадение выражающихся через нее характеристик, в частности асимптотической дисперсии и эффективности.

Рассмотрим класс M -оценок масштаба S , задаваемых неявным уравнением

∑ χ(xi / S) = 0, где х — некоторая оценочная функция, обычно четная и неубывающая при x > 0. Выбирая вид функции х, можно получать различные как робастные, так и неробастные оценки масштаба. Этот класс был введен Хьюбером и подробно рассмотрен в [2; 3].

Известно, что функция влияния таких оценок с точностью до нормирующего множителя совпадает с выбранной оценочной функцией IF ( x ; S , F) x х ( x ). Воспользуемся этим фактом и построим М -оценку масштаба M _a , приближающую Q , положив

Х_а ( x ) = c a — a ' ( Ф ( x + a ) - Ф ( x - a )), a > 0,

в случае четной монотонно возрастающей при x > 0 функции х ( x ). Эти условия будут выполнены при [0; 2], причем при нуле достигается максимум s ^ = 29,3 % (рис. 2).

где Ф ( x ) - стандартное нормальное распределение; c _a выбирается из условия состоятельности оценки J x ( x ) d ( x ) = 0. При a = Ф ^-1(5/8) 72 = 0,450 6 функ

ция влияния соответствующей оценки M _a будет совпадать с IF ( x ; Q , Ф ) [5].

Основной результат. Для удобства будем рассматривать другое параметрическое семейство, взяв первые несколько членов разложения Ф ( x ) в ряд Тейлора:

Х а ( x ) = c a — 3 (6 — a ² ( x ² - 1)) ф ( x ), c a =

= (12 - a ²) / (12 77).

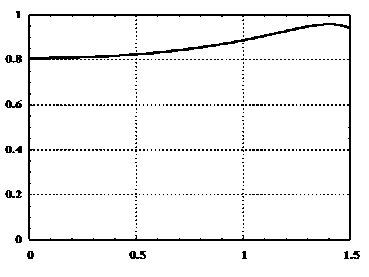
Рис. 1. Эффективность оценки в зависимости от параметра a

Такое представление позволит получить результат в явном виде через элементарные функции.

Из-за своей простоты также будет интересен частный случай при a = 0:

X a ( x ) = 1 / 7л - 2 ф ( x ).

Исследования показали, что не имеет смысла рассматривать разложение с большей точностью: выигрыш в характеристиках минимален, а объем вычислений возрастает. В качестве альтернативы можно взять функцию x_a p ( x ) с произвольным полиномом второй степени от x ², но в свете полученных результатов это также представляется избыточным.

Получим характеристики предложенной оценки. Формула для асимптотической дисперсии M -оценок масштаба выглядит следующим образом [3]:

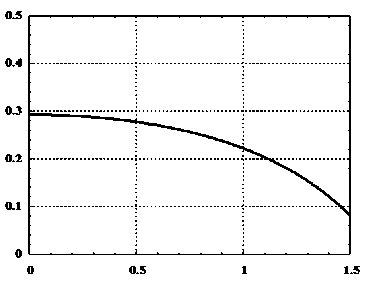
Рис. 2. Пороговая точка оценки в зависимости от параметра a

Вычисление оценки как решения неявного уравнения в большинстве случаев затруднительно, но при этом возможно применение итеративных схем. В частности, можно ограничиться первой итерацией, получив так называемую M -оценку [2]:

V ( M _a , Ф) = J IF ² ( x ; M _a , Ф) d Ф( x ) =

/Х 2 ( x ) ф ( x ) dx

( J xx' _a ( x ) ф ( x ) dx )²,

ST = ST

—

Lx ( x / S ) d S ^EX ( x - / S )

S = S<⁰>

.

что дает выражение для эффективности

1 e„ =----------=

^a 2 V ( M _a ,Ф)

=________________ 81( 0 2-4) 2_________________

" 8(432(273 - 3) - 24(873 - 9) a ² + (1673 - 9) a ^4.

Максимальная достижимая эффективность составляет 95,9 %, но даже при a = 0 она не опускается ниже уровня 80,8 % (рис. 1).

Пороговая точка оценки определяется соотношением

-Х а (0)    = 12(72 - 2) - (72 - 4) а ²

Х а И -Х а ^{(0)        4(} « ² - ⁶⁾

Начальное приближение должно быть само по себе в высшей степени робастно. Подставляя предложенную оценочную функцию, получаем, что одношаговая оценка при a = 0 задается как уточнение медианы абсолютных отклонений:

M_n = 1,483 MAD ■1 1 - Z ⁰ n /^2 ⁰                    I           7

V        Z 2

r-7 X ¹ k - u ² /2

Z k L u - e i , u -

x i - med x

.

1,483 MAD

Множитель перед MAD необходим для того, чтобы обеспечить состоятельность оценки на нормальном распределении.

Следует отметить, что функция влияния, а значит асимптотическая дисперсия и эффективность одношаговой оценки, будут несколько отличаться от первоначальных теоретических результатов. Но важным свойством таких оценок является то, что они наследуют пороговую точку начального приближения [6]. При выборе в качестве основы медианы абсолютных отклонений пороговая точка одношаговой оценки M α повышается до 50 %.

Сравнение оценок. Приведем численные результаты статистического моделирования оценок при 50 000 испытаний на стандартном нормальном распределении (табл. 1). Параметр α имеет значение 0,450 6, что обеспечивает совпадение основных асимптотических характеристик оценок Mα и Q. Время вычисления оценок в миллисекундах соответствует конфигурации Intel Core i7 с частотой 2,8 ГГц. Влияние отклонений от идеальных условий проверялось на модели больших ошибок Тьюки вида (1 – ε) Φ(x) + ε Φ(x/σ) при ε = 0,1, σ = 3. Результаты моделирования представлены в табл. 2. Таким образом, предложена оценка масштаба, имеющая такую же функцию влияния, асимптотическую дисперсию и эффективность, что и часто используемая оценка Qn. Результаты моделирования показывают, что одношаговый алгоритм вычисления оценки не только требует значительно меньшего времени, но и обеспечивает меньшее смещение относительно оцениваемой величины, особенно на малых выборках. При подстановке медианы абсолютных отклонений в качестве начального приближения пороговая точка имеет максимально возможное значение 50 %, а свободный параметр позволяет повысить эффективность оценки до 95 %.