Приближенная оптимизация управления в параллельных вычислениях

Приближенные и вычислительные методы – обширная и ставшая самостоятельной область исследований и разработок в теории оптимального управления, нацеленных на эффективное решение практических задач. Исторически развитие этих методов началось одновременно с созданием современной теории оптимального управления. В числе основоположников отметим Д. Е. Охоцимского, В. А. Егорова, Т. М. Энеева, Л.И. Шатровского, Дж. Келли.

Одно из направлений в этой области базируется на достаточных условиях оптимальности Кротова и принципе расширения. Его плодотворность подтверждается многолетними разработками [1] – [4], отличающимися значительным многообразием подходов и результатов. В основном это различные итерационные процедуры улучшения управляемых процессов, как и в других школах. Спецификой является возможность априорного оценивания получаемых приближенных решений и использование характерного свойства вырожденности прикладных задач и соответствующих специальных методов для поиска начальных приближений, что, как известно, является критическим моментом при использовании итерационных улучшающих алгоритмов. В последнее время интенсивно развиваются новые методы, ориентированные на параллельные вычисления на суперкомпьютерах кластерного

¹ Работа выполнена при частичной финансовой поддержке Российского фонда фундаментальных исследований (проекты № 08-01-00274 и № 09-01-00170).

типа с учетом высокой степени возможного параллелизма, обусловленного самой природой рассматриваемого класса задач как задач систематического сравнения вариантов с параметрами, распределенными в пространстве состояний.

Цель данной статьи – представить собственный опыт работы в этом направлении, связанный с созданием, развитием и приложениями программно-алгоритмического комплекса улучшения и приближенно оптимального синтеза управления (ПК ISCON) [5].

1.    Комплекс алгоритмов улучшения и оптимизации управления

Алгоритмы ПК ISCON формализованы исходя из задач управления непрерывной и дискретной системой в стандартной форме:

x = f ( t , x , u ), t e T = [ t , , t_F ], (1) x ( t + 1) = f ( t , x ( t ), u ( t )), t e T = t , , t , + 1,..., t_F , (2)

x e X( t ) c R n , u e U( t , x ) c R p , x ( t_F ) e Г, I = F ( x ( t F )),

( t , , x ( t , ), t_F ) заданы, F : R n ^ R . Реализуемые здесь методы построены или строятся на следующих принципах. Систематически применяются различные приближенные преобразования модели объекта с целью упрощения для эффективного поиска приближенных решений и их оценок. В частности, улучшение рассматривается как оптимизация в окрестности текущего приближения на упрощенной аппроксимации модели объекта. На этапе вычислений производится дискретизация непрерывных моделей управляемых систем, и задачи рассматриваются в дискретной постановке.

В соответствии с теорией Кротова при помощи произвольной функции ^ (t , x ) строятся следующие конструкции:

R ( t , x , u ) = ^ ( t + 1, f ( t , x , u )) - ^ ( t , x ), G ( x ) = F ( x ) + ^ ( t_F , x ) - ^ ( t , , x ( t , )).

В этих терминах на основе достаточных условий оптимальности и улучшения разработаны методы и комплекс алгоритмов приближенной оптимизации управления (улучшения и приближенно-оптимального синтеза).

Комплекс алгоритмов состоит из трех крупных блоков (АППРОКСИМАЦИЯ, СИНТЕЗ, УЛУЧШЕНИЕ) и предназначен для решения трех типов задач: (I) глобальный приближенно-оптимальный синтез управления; (II) улучшение и локально-оптимальный синтез управления и (III) управление в реальном времени. Задачи типа (I) в наибольшей степени отвечают указанной выше проблеме синтеза, однако требуют наибольших вычислительных ресурсов. Задачи типа (II) возникают в тех случаях, когда вычислительные трудности глобального синтеза оказываются непреодолимыми и заставляют решать проблему в два этапа. Вначале ищется оптимальная программа управления итерационными методами последовательного улучшения, и соответствующая траектория. Затем в некоторой достаточно малой окрестности последней строится приближенно-оптимальный синтез с требуемой точностью при предположении, что действующие возмущения не приводят к выходу результирующих траекторий за пределы этой окрестности. Локализация позволяет существенно уменьшить требования к вычислительным ресурсам за счет сужения расчетной области и возможного упрощения модели объекта с целью использования аналитических методов. Задачи типа (III) связаны с практической реализацией найденных законов управления, вычислительных экспериментов с целью адаптации их к реальным условиям функционирования управляемых систем. Здесь большое значение имеет принятая концепция управления как дискретного во времени. Она позволяет принципиально разделить этапы наблюдения-анализа текущей ситуации и принятия адекватных управленческих решений. Такое разделение делает полученные результаты не зависящими от принятого метода решения задачи наблюдения, следовательно, существенно расширяет круг возможных практических приложений в сравнении с подходами, где оба этапа не разделены.

Блок АППРОКСИМАЦИЯ предназначен для аппроксимации моделей объектов управления и функций Кротова при решении задач улучшения и синтеза. По существу он универсален и может использоваться для любых многомерных объектов. Аппроксимация про- изводится в среднем по методу наименьших квадратов (МНК). Этот хорошо известный метод в данном случае дает возможность «развязать» аппроксимирующую конструкцию и сетку значений аппроксимируемой функции, которые при многомерной интерполяции жестко связаны. В частности, он позволяет генерировать регулярные («прямоугольные») сетки с постоянным или переменным шагом по каждой переменной, что очень важно для распараллеливания вычислений. Некоторые детали реализуемых в нем алгоритмов приводятся в нижеследующих описаниях основных блоков, где они интенсивно применяются.

2.    Описание блока СИНТЕЗ

В этом блоке сосредоточены алгоритмы, реализующие метод приближенного синтеза оптимального управления для дискретных моделей управляемых систем на основе среднеквадратической аппроксимации (в частности, на интерполяции) соотношений динамического программирования при полиномиальном представлении функции Кротова-Беллмана [6]. При этом рассматривается постановка задачи «со свободным правым концом»:

X ( t ) = Г = R n . Фазовые ограничения, в том числе на правом конце, могут быть учтены с помощью известного метода штрафов.

Функция Кротова ф выбирается в общем случае так, чтобы в окрестности некоторой опорной траектории приближенно выполнялись соотношения типа Беллмана:

P ( t , x ) = ф ( t , x ) - H ( t , x , ф ( t + 1, x ) ) = 0 , G ( x ) = ф ( t_F , x ) + ( 1 - a ) F ( x ) = 0 ,

H (t, x, ф(t +1, x)) = max | ф(t +1, f (t, x, u)) a(u — u (t))2 1 ueU (t, x )l                                   2

Опорной может быть приближенно оптимальная, либо улучшаемая траектория, если синтезируется улучшающее управление, u ( t ) - улучшаемое управление, 0 <  a <  1 - регулятор метода улучшения. При отсутствии опорной траектории принимается заведомо a = 0.

Аппроксимация функции Кротова производится некоторым многомерным полиномом ф( t, x) = Jv (t) gi (x),(3)

i = 1

где    g (x) = ( g 1( x),..., ga (x)) T    - набор заданных базисных    функций,а

V(t) = (v1 (t),...,уа(t))T - набор коэффициентов, подлежащих определению из условий min У (vT (t)g(x^ (t)) — H(t, xp (t), V (t +1)g(x^ (t))))2,(4)

v(t) “ min £ (vT (tF)g(xp (tp)) + (1 — a)F(xp (tp )))2 ,(5)

V( tF ) д в - номер узла сетки. Условия (4), (5) сводятся к решению системы линейных алгебраических уравнений A(t)[уа (t)] = B(t) относительно коэффициентов v(t) аппроксимирующего полинома.

В качестве аппроксимирующих использовались два типа конструкций. Первый тип – композиция одномерных полиномов m1

f

m ₂

f    m n

n

ф ( t , x ) = ^ ( x ¹ ) j У ( x ² ) j 2 ^ ^ V

./ 1 = 0

V j 2 = 0

V    j n = 0

j ₁ , j ₂ , … , j

, ( xⁿ ) ^/n 1 n

,

допускающая интерполяцию на регулярной сетке с числом узлов m_i по переменной x_i .

Второй тип – регулярный полином порядка n

ф(t, x) = V(t) + VT (t)x + -^ xT^(t)x + ... , где VT (t) - n -мерный вектор, a(t) - матрица n x n.

В вычислительном плане наиболее удобно строить постоянную во времени прямоугольную сетку Х р ( t ) = const, покрывающую область, где строится синтез. С этой целью (2) преобразуется к новым переменным – отклонениям от опорных значений.

Близость полученного приближенного синтеза оптимального управления ~ ( t , x ( t )) к строгому оптимуму можно определить с помощью следующей верхней оценки Кротова:

А ( t ) = А ( t + 1 ) + max P ( t , x ) - min P ( t , x ) xx

A(tF) = max G(x) - min G(x), xx где x пробегает заданную область. Найденное управление тем ближе к оптимальному, чем меньше эта оценка. Возможность вычисления оценки – это важное преимущество перед «чистым» методом Беллмана. Она позволяет организовать регулярную процедуру уточнения приближённого решения за счет увеличения числа узлов интерполяции и их расположения в фазовом пространстве, а также дает критерий ее остановки.

Схема соответствующего алгоритма представлена в общем виде на рис. 1 и более подробно на рис. 2, 3.

Важную роль здесь играют алгоритмы задания эффективных начальных приближений по методу восстановления функции цены (МФЦ) [6] в случае магистральных решений, характерных для многих прикладных задач оптимального управления. В этом случае аппроксимирующая конструкция для функции Кротова модифицируется следующим образом: ф = ф ⁰ + ф , где ф⁰ - приближение по МФЦ, ф - полином (3).

Cell

Генерация

Рис. 1

Задание аппроксимирующего полинома

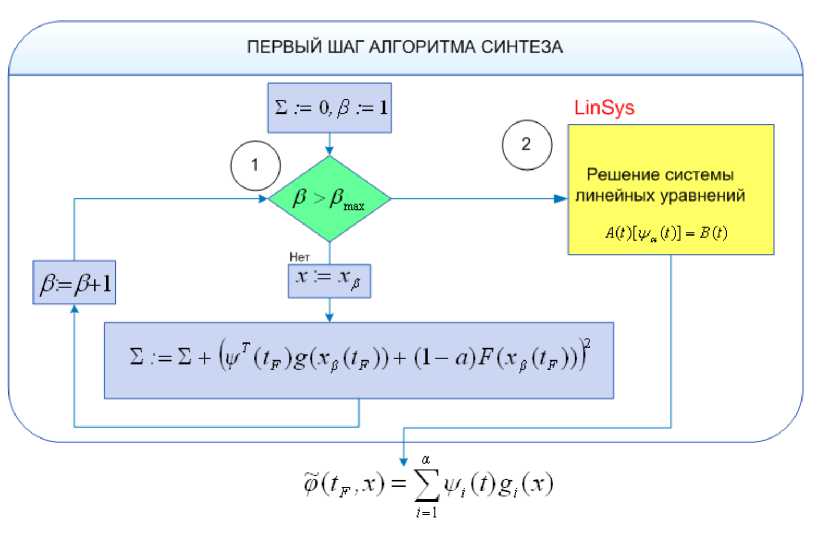
Рис. 2

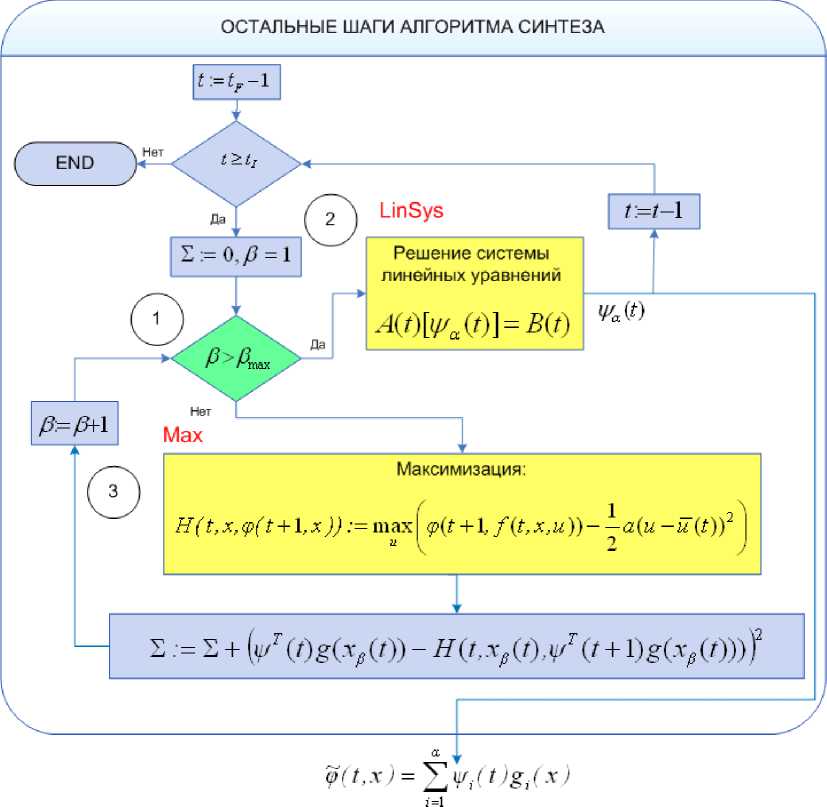
Рис. 3

Достаточно легко реализовать параллельность описанного алгоритма при переборе значений в . Область формирования сетки разбивается на части, в каждой из которых строится часть матрицы A ( t ) и часть столбца свободных членов B ( t ) для системы уравнений с помощью исходных значений в узлах текущей части. Общая матрица получается в этом случае, как сумма всех построенных «частичных» матриц (это же справедливо и для свободных членов). На рис. 2, 3 этот вид потенциального параллелизма обозначен цифрой 1. Решение системы линейных алгебраических уравнений (обозначено цифрой 2 на рис. 2, 3) и поиск максимума функций многих переменных (обозначены цифрой 3 на рис. 2, 3) можно отнести к другим видам потенциального параллелизма. Как показывает практика, программная реализация этих видов параллелизма эффективна лишь при больших размерностях n , p исходной динамической системы (2).

3.    Описание блока УЛУЧШЕНИЕ

В этом блоке сосредоточены алгоритмы, реализующие методы первого и второго порядка улучшения управления для дискретных моделей управляемых систем. Один из них основан на полиномиальном задании функции Кротова (3) и среднеквадратической аппроксимации соотношений Кротова-Беллмана (4), (5) в окрестности улучшаемой траектории и по существу описан в предыдущем разделе. Получаемый синтез при достаточно большом значении а обеспечивает улучшение.

Другой метод основан на конечно-разностных аппроксимациях тейлоровских разложений вышеуказанных соотношений. Рассмотрим его подробнее.

Имеется элемент     m1 = (т, x1 (t), u1 (t))e D, требуется найти элемент т11 = (t, x11 (t),u11 (t))e D, такой, что 1 (т") < 1 (m1). Общие конструкции метода улучшения управления приведены в [4], где т1 ищется как аппроксимация решения задачи:

y ( t + 1) = g ( t , y ( t ), v ( t ) ) , t e T = { t₁ , t₁ + 1, ™ , t_F } ,

y ( t + 1) = y ( t ) + - £ v_; ( t ), y ( t, ) = 0, y ( t, ) = 0,

• ² i = 1

Fa (У 0(tF), У (tF)) = ay 0(tF) + (1 - a)F(y(tF) + x (t)) ^ min, где a - некоторое действительное число из полуинтервала (0,1] (регулятор метода), g(t, y(t), v(t)) = f (t, y(t) + x1 (t), v(t) + u1 (t))- f (t, x1 (t), u1 (t)), x = y + x1, u = v + u1.

Функция Кротова ищется в виде ^ ( t , у °, y ) = V (t ) + у ⁰( t ) y ⁰ + y ^T ( t ) y + ^ y^T ^ ( t ) y . Значения V ( t_F ), у ⁰ ( t_F ), y ^T ( t_F ), < 7 ( t_F ) находятся из условий

V (t F ) =- F a (0), у 0 ( t F ) =- a , у ( t F ) =--1- ( F a (01 Y ^ xЦ) — F a (0) ), i = U ,

Y ^ x i

^n ( t F ) = - ( F a (01 2 Д i / i ) - F a (01 Y x i / i ) + F a (0) ), i = U , ^{( Y} ^ x i )

° , ( t - ) =- Т ^Д^ДГ ( F a (01 Y^ x i" , YA x -/, ) - F a (°' Y l x i / i ) - F a ® ¹ > A x - / , ) ⁺ F a Й i *1 = 1^ n • где Y — некоторое действительное число (регулятор метода), A x_i , Д u , - масштабы переменных x_i , u , . Здесь через F a (01 YA x_i / _i ) обозначено значение функции F a в точке

⁽ y °, У 1 ^, ™ ^, yi - 1 , y i , y i + 1 . ™ . У п ) = ^(0,0, ™ ^,0, Y^x i ^,0, ^ ^,0).

Вводится в рассмотрение функция

H a ( t , y , v ) = V (t + 1) - a ^Tv² + y ^T ( t + 1) g ( t , y , v ) + ¹ g ( t , y , v ) ^T ^ ( t + 1) g ( t , y , v ).

2 i = 1                                  2

Эта функция разлагается в ряд в окрестности нуля:

H_Q ( t , y , v ) = H_Q ( t ,0,0) + y^TH_a y ( t ,0,0) + 2 y T H ayy ( t ,0,0) y +

+ ^ v^TH_a v ( t ,0,0) + v^TH_ayv ( t ,0,0) y + 1 v^TH_avv ( t ,0,0) v j

Из условия max^vTHOv (t,0,0) + v^ (t,0,0)y + 2 vTHttVV (t,0,0)v^ = 0, t e T \ {tF }, получается v1 (t, y) = arg max| vTHav (t,0,0) + vTH(t,0,0)y +1 vTHavv (t,0,0)v | = v V                                 2               )

= - H ^ ( t ,0,0) ( H_QV ( t ,0,0) + H_Q y _V ( t ,0,0) y ),

v ( t ) = H a ( t ,0,0), V ⁰( t ) =- a , V ( t ) = H_a y ( t ,0,0), a ( t ) = H ayy ( t ,0,0), t e T \ { t F } . Последние равенства, после замены производных их разностными аналогами, принимают вид:

v¹ ( t , y ) = - N ;*( t ) ( M a ( t ) + p -Т ( t ) y ), t e T \ { t F } ,

N j ( t ) = .-V.    ⁽ H a (^{0I 2 S X} u ,/n +, ) - ^Ha (^0I u - / n + ) + ^Ha (^ ¹ j = ^ ,

^{( J A u} j )

< N (t) = — ----(H (0I JAu., „ JA u.   ) - H (0I JAu., J - kj        J2AukAu,     a           k/ n+k,      j/ n+,        a           k/ n+k

- H a (0I J A u , / n + , ) + H a (0) ) k , j = 1^ ,

M i ( t ) = Ju~ (H . (0 ^{I 5 1} u j / n . j ) ^- H a ««l j = 1. P ,

‘ P j ( t ) = !® X¹ _Aur_i ( H - (0^I Ya X j/i ■^{5 4} “ j / n . j ) ^{- H} - (°^I Ya x j,i ) ^{- h}. (0 ^I 5 i »„ n . j ) ⁺ H a (0) 1

i = 1, n , j = 1, P ,

V (t ) = H a (0), V °( t ) = - a , V . ( t ) =      ( H a (0I y A x .,) - H a (0) ), i = 1, n ,

^{YA x}.

^a- ( t ) =          ( H a (01 2 Y x . / . ) - H a (01 ) A x . / , ) + H a (0) ), i = 1, n ,

J           ( j A r . ⁾

° j ( t ^} = _{Y 1 X A X} ( H a (^0I Yx" i , YA X j / j ) ^- H a *⁰4 ^A X i - i ) ^- H a W Y .X / j >  ⁺ H a (0) )

_                      i, j = 1, n, t e T \ {tF }, где 5   - некоторое действительное число (регулятор метода). Здесь через

В,(0I lAxн■,5Au.   ) обозначено значение функции H„ в точке a4           i / I ,       j I n + j7                                          Ту                 a

(t, y!,_, yi _p yi, yi+1,™, yn, vp™, v, _p v, , v,+1,..., vp) = (t ,0,^,0, yAxi ,0,...,0,0,...,0,5A u, ,0,^,0). Полагается u" (t, x) = v11 (t, y + xI (t)) + u1 (t), t e T \ {tF }.

С помощью уравнений системы (2) находится соответствующая пара (u¹¹ ( t ), x¹¹ ( t ) ) . Полученный таким образом элемент m¹¹ = ( t , x¹¹ ( t ), u¹¹ ( t ) ) e D и будет улучшением.

Замечание 1. В случае алгоритма первого порядка функция Кротова ищется в виде ^ ( t, у °, у ) = V ( t ) + у ⁰( t ) у ⁰ + V ( t ) у.

Следовательно, для этого случая все соотношения вышеописанного алгоритма второго порядка остаются в силе, если только положить а ( t ) = 0, t е T .

Схема описанного алгоритма представлена на рис. 4.

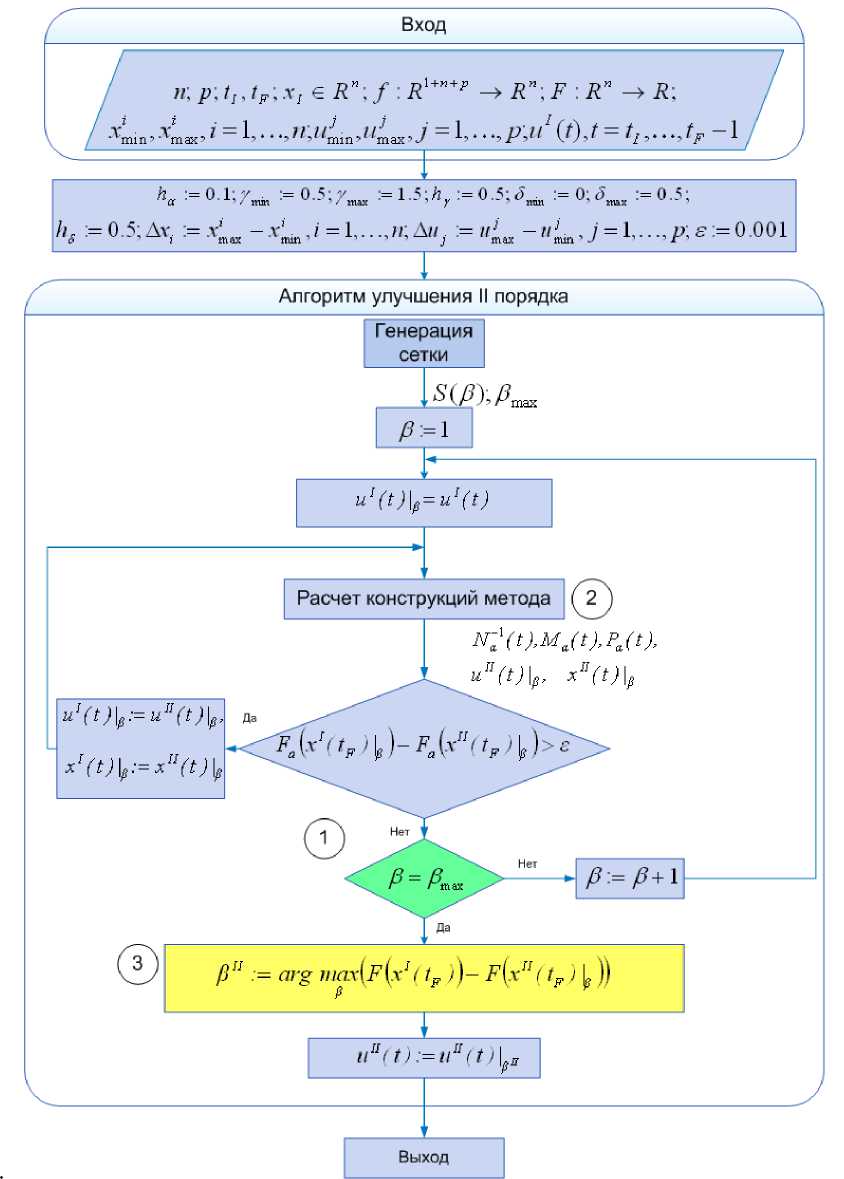
Рис. 4

Из блок-схемы алгоритма (рис. 4) видно, что расчет конструкций метода и прямой счет при нахождении управления в форме синтеза могут выполняться независимо для каждого набора параметров алгоритма (для каждого значения β ). На рис. 4 этот вид потенциального параллелизма обозначен цифрой 1. При этом число итераций для различных наборов параметров заранее неизвестно и в общем случае различно, что затрудняет процесс равномерной загрузки вычислительных узлов при программной реализации данного вида параллелизма. К другим видам потенциального параллелизма можно отнести операции матричного исчисления (обозначены цифрой 2 на рис. 4) и поиск максимума функций многих переменных (обозначены цифрой 3 на рис. 4). Как показывает практика, программная реализация этих видов параллелизма эффективна лишь при больших размерностях n , p исходной динамической системы (2).

4.    Параллельная реализация и вычислительные эксперименты

В целом анализ показывает, что данный алгоритмический комплекс обладает большим потенциальным параллелизмом. С учетом того, что число итераций в алгоритмах улучшения заранее неизвестно, динамическое распараллеливание предпочтительнее любых других типов. Эту концепцию автоматического динамического распараллеливания программ реализует Т-система — оригинальная российская разработка [7]. Она предоставляет язык программирования T++ (очень простой параллельный диалект С++), который предназначен для эффективной реализации динамического распараллеливания.

Вышеописанные алгоритмы были реализованы в виде исполняемых модулей ПК ISCON с учетом возможностей распараллеливания. Была проведена большая серия вычислительных экспериментов, с использованием методических примеров и прикладных задач, связанных с исследованием маневров безопасной нештатной посадки вертолета с определением границы безопасной зоны [8] и стратегий устойчивого развития регионов на их социо-эколого-экономических моделях.

Задача о посадке вертолета показательна тем, что потребовала использования различных аппроксимаций имитационной модели движения вертолета, не имеющей полного аналитического описания: силы и моменты, действующие на вертолет, были заданы лишь в форме компьютерных программ. Вначале была получена линейная аппроксимация модели объекта, на которой был проведен качественный анализ, в результате него сформировалось грубое начальное приближение глобально-оптимального управления. Далее это управление улучшалось на более сложной, нелинейной аппроксимации модели объекта с использованием рассмотренного выше алгоритма улучшения. Результаты для наиболее жесткого из рассмотренных сценариев нештатной ситуации уже после трех итераций позволили сделать вывод о повышении границы опасной зоны на 15% за счет оптимизации соответствующего посадочного маневра. Эффективность параллельной реализации программ при решении этой задачи демонстрируется в таблице 1.

Таблица 1

Программа аппроксимации модели динамической системы с помощью МНК
Число процессоров (ядер)	1	3	5	7	9	11
Время работы программы, c	3338.35	1237.14	729.92	632.00	631.21	588.02
Ускорение	1	2.70	4.57	5.28	5.29	5.68
П	рограмма улучшения управления
Число процессоров (ядер)	1	3	5	7	9	11
Время работы программы, c	1029.85	351.99	218.83	159.60	130.71	110.29
Ускорение	1	2.93	4.71	6.45	7.88	9.34

Для исследования стратегий устойчивого развития использовалась одна из последних версий динамической социо-эколого-экономической модели региона, включающая блок активных инновационных процессов [9], которая не могла быть реализована в полном объ- еме на обычных компьютерах. Для практических вычислений требовались различные упрощающие допущения и высокая степень агрегирования. Появление доступных суперкомпьютеров открывает новые возможности многовариантных прогнозных и оптимизационных расчетов с участием экспертов и руководителей-практиков при разнообразных внешних воздействиях и неопределенностях. В особенности это связано с исследованием инновационных процессов. Понятие “инновация” трактуется формально как любое целенаправленное изменение параметров, число которых, как правило, велико, что без искусственного агрегирования ведет к драматическому росту размерности пространства состояний.

Один из наиболее трудоемких, но неизбежных этапов исследования модели является двухступенчатая процедура оптимизации. На первом шаге этой процедуры при упрощающих допущениях находится приближенное магистральное решение, на втором – восстанавливаются исходные допущения и производится улучшение приближенного магистрального решения с использованием вышеописанного универсального алгоритма итерационного улучшения.

Описанный алгоритм оптимизации и некоторые другие алгоритмы (анализ чувствительности, сценарный анализ и т. п.) для социо-эколого-экономической модели реализованы в Т-системе. В вычислительных экспериментах по оценке эффективности распараллеливания программ были использованы наборы данных для Переславского [9] и Байкальского регионов.

Для Переславского региона суммарная размерность вектора состояния составила 54, а вектора управления - 56. Вычисления проводились на суперкомпьютере СКИФ МГУ «Че-бышёв» для 160 различных наборов параметров метода улучшения. Проводился запуск программы на различном числе узлов с замером времени работы. Полученные данные представлены в таблице 2.

Таблица 2
Программа улучшения управления
Число процессоров (ядер)	1	4	8	16
Время работы программы, с	10331	4184	2262	1160
Ускорение	1	2.469	4.567	8.906

Для Байкальского региона набор данных был сформирован совместно со специалистами БГУ, Бурятского и Иркутского научных центров СО РАН. Общая размерность вектора состояния, составила 3551, а вектора управления - 3588. Были проведены тестовые сценарные расчеты по анализу чувствительности целевого функционала к изменению элементов матриц прямых затрат и коэффициентов воздействия экономики на природный комплекс. Расчет в последовательном варианте занял около 6 часов. Вычислительные эксперименты с параллельной версией программы на суперкомпьютере СКИФ МГУ "Чебышёв" дали результаты, представленные в таблице 3.

Таблица 3

Программа анализа чувствительности
Число процессоров (ядер)	8	19	38	64
Время работы программы, с	3466	1483	785	520
Ускорение	6	15	28	42

Заключение

В целом на основании проведенных исследований можно заключить, что реализация разнообразных приближенных методов на суперкомпьютерах кластерного типа открывает новые перспективы их эффективного применения для решения сложных прикладных задач, немыслимые ранее при использовании обычных компьютеров. В частности, это относится к практически значимым версиям модели со сложной системой данных, в которых учет ин- 27

новационных процессов без искусственного агрегирования приводит к драматическому росту размерности.

С другой стороны и задачи, связанные с оптимизацией и в целом с исследованием моделей объектов управления, как многовариантные, естественным образом приспособлены для параллельных вычислений на кластерах и не требуют сложных процедур распараллеливания. При определенной организации многовариантных вычислительных экспериментов и трактовке их результатов они становятся инструментом не только трудоемких количественных оценок, но и качественного анализа, позволяя выделить ведущие факторы, переменные и параметры, на которых требуется сосредоточиться при последующих эмпирических исследованиях.