Приближенное аналитическое решение внутренней задачи кондуктивно-ламинарной свободной конвекции

Математическое моделирование свободной конвекции в большинстве случаев базируется на уравнениях Навье-Стокса в приближении Обербека-Буссинеска. Изучению внутренних задач свободной конвекции посвящено много работ, поскольку они имеют важные практические приложения, такие как хранение криогенных жидкостей, охлаждение электроники, моделирование двигателей внутреннего сгорания и др. Исследованию течения и теплообмена при ламинарнойсвободной конвекции между вертикальными параллельными изотермическими пластинами с различными температурами методом конечных объемов посвящена работа [1]. В работе [2] модификацией метода конечных разностей решается краевая сопряженная задача нестационарного конвективного теплопереноса в замкнутой квадратной полости. Ламинарная свободная конвекция внутри параллелепипеда с нагревом боковых стенок численно исследована в работе [3]. Изучению свободной конвекции в квадратной области с внутренней перегородкой методом конечного объема посвящена работа [4]. В работе [5] конечно-разностным методом исследуется течение наножидкости в пористой квадратной каверне. В подавляющем большинстве работ применяется численное моделирование. В связи с этим возникает необходимость получения аналитических и приближенно аналитических решений подобного класса задач.

Постановка задачи и вывод основных уравнений

Рассматривается плоская  квадратная область (рисунок 1), заполненная полностью вязкой несжимаемой жидкостью. В начальный момент времени жидкость находится в состоянии покоя с температурой t0. Затем температура левой стенки мгновенно принимает значение t , причем тепловой поток через верхнюю и нижнюю стенку отсутствует q=0. Температура правой стенки поддерживается постоянной, равной температуре жидкости в начальной момент времени (th > t0).

В выбранной системе координат уравнения Обербека-Буссинеска принимают следующий вид:

Sv_x     Sv_x     Sv_x     1 S p     fS²v_x   S²v_x )

- + v_x x +     x = + v    x + x ,

St     S x    y S y     p S x   ( S x ²    S y _y

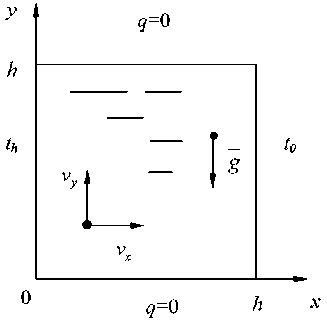
Рисунок 1. Расчетная схема

Figure 2. Design diagram

S v y      S v y      S v_y    1 S p

--+ v_x --+ v y ---— —     +

St    S x     S y    p S y

^{f S 2} v_y   ^{S 2} v,

I      y + y

( Sx²    Sy²

S t       S t       S t

St

+ v + v — a

S x

S y

⁺ P gt,

' S ² 1    S ² t )

₍s x ²    S y ² J ,

S vx    S vy

—x + — y — 0 .

S x    S y

Здесь v , v – компоненты скорости по осям

x и y ; p , t , t - давление, время и температура; p , v ,a , в - плотность, коэффициенты кинемати-

ческой вязкости, температуропроводности и объемного расширения среды. Поскольку рассматриваются очень медленные течения, то без потери физического смысла предположим, что v_x ~ 0, v_y ~ 0. При такой линеаризации получим

Sv,     1 Sp    f 92 v9

xxx

—+ v

St p S x   ( S x ²

Sv     1 Sp   f S2 v y —+ v   y ++

St    p S y   ( S x ²    S y J

S t     f S ² 1   S²1 )

^{— a +}

St   (S x²  S y J

S vx   S vy

—^x + —- — 0.

S x    S y

Для сокращения числа гидротермических параметров система (1)--(4) приводится к безразмерному виду введением масштабов для зависи-

т      x мых и независимых переменных: 9 — —, X — —,

Y — y ,   V x — v x- ,   V y — vr , p — p , t — l t »

h          v           v          P      t h ^— t 0

.Здесь h – длина стороны квадратной области, т, v, p - характерные время, скорость

и давление, t_h — 1 ₀ - характерная разность температур.

Характерное время вязкого затухания давление, время и скорость вычислим из урав-„  - т ,  1 pт 1 VT . ы _ нений у— — 1,--— — 1, — — 1. Имеем h2     р h v      h

- ^{h 2} - V - V²

т — —, v — —, p — р — . Перепишем уравне-

V      h       h ние (1) в безразмерных переменных:

Обезразмеренное уравнение (3) примет вид

д T _ 1 ( д ² T  д ² T 1

—            +, де Pr 1дX2  дY2 )

дVx __др  д2Vx  д2Vx де - дX  дX2  дY2 ■

Уравнение (2) примет вид д——8JL+a2v+ V+Gr T, де    д Y  дX2   д Y2

h ³

где Gr = —fi g ( tw — t o ) — число Грасгофа. Исключим давление из уравнений (5) и (6):

д ^у де 1д X

—

д ²

⁺ д Y²

д V - ) д Y )

(д V

д ² д X²

д V..

д X

—

д V 1

—- + д Y )

—

д V -

д X  д Y

_ д T + Gr— дX

где Pr – число Прандтля.

В начальный момент времени жидкость находилась в состоянии покоя и имела всюду одинаковую температуру 1 ₀, поэтому начальные условия для функции токаи температуры имеют вид:

Ф ( X , Y ,0) = 0,            (10)

t ( x , y ,0) — 1 ₀, следовательно

T ( X , Y ,0) — t ⁰- ^— t ⁰ — 0.          (11)

t h ^— t 0

Поскольку температура левой стенки скачком изменяется до температуры t h , а температура правой 1 ₀ не изменяется, граничные условия на    температуру имеют вид

t (0, y , т ) — t h , t (1, y, т ) — 1 0, или

Безразмерный вихрь обозначим

д V Q — —y- д X

—

д V x , тогда д Y до д2 О д2^  _ дT

--- — --- 77 +-- 77 + Gr---, де  д X ²   д Y ²     д X

t (0, y , е ) — t^-t ° — 1, t (1, y , е ) — t °— t ⁰ — 0    (12)

t h ^— t 0                        t h ^— t 0

Условия непротекания и прилипания жидкости выражаются уравнениями

Уравнение неразрывности (4) примет вид д V  9 V

—- +-- - — 0.

д X  д Y

Чтобы оно удовлетворялось автоматически, введем функцию тока V следующим об-

ф (0, y , е ) = ф (1, y , е ) =

— ф( x ,0,е) = ф( x ,1,е) = 0, дФ(0, Y ,е) = дФ(1, Y ,е) = дX      дX

_ дФ( x ,0, е ) _ дФ( x ,1, е ) ₌

=    д Y    ” д Y       '

дУ        дУ разом:   Vx — — , V —-- x  д Y      y   дX

.

Получим

д V П — —y

—

д V _ д ² У  д ² V

---

д X   д Y

д X ²    д Y ²'

Перепишем

уравнение (7) через функцию тока:

д (д2У  д2У1_д4V   д4V де laX2^Sy2 J —дХ4 + дх 2д y 2 +

В переменных «вихрь-функция тока» исходная система (1)–(4) сводится к нестационарному уравнению теплопроводности (9) и нестационарному неоднородному бигармониче-скому уравнению (8) с начальными (10)–(11) и краевыми условиями (12)–(14).

Решение задачи

д ⁴ V    д T

+ —г — Gr—.

д Y ⁴     д X

V

Введем переменную Ф — — и получим Gr уравнение уже без числа Грасгофа д (д2Ф  д2Ф1  д4Ф

+—+ де 1дx2  дy2)д д4Ф   д 4Фд

+--7.------77 +--7.

дX2дy2  дy4

Несопряженный характер системы (8)– (14) позволяет последовательно решать тепловую – (9), (11), (12), и гидродинамическую – (8), (10), (13), (14) задачи.

Решение тепловой задачи известно

т ( x , y , е ) = 1 — x +- У ^-)- х п p =1 p

х sin [ ( 1 — X ) п p ] exp

Pr

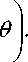
К системе (10), (12), (15), (16) применим интегральное синус-преобразование Фурье с конечными пределами [8] по переменной X :

Ф₍ = ^[ Ф ( X , У , 0 ) ] =

1                                        (16)

= _JФ ( X , У , 0 )sin ^ X ) dX = Ф_У ( Я , У , 0 ) 0

Обозначим через

8 ² Ф (1, Y , 0)    , _х 8 ² Ф( 0, Y , 0)

A =----- ⁽ ’ , ) , B ( Y, 0) =----- ⁽ ’ ’ )

8 X ^{2       v 2}       8 X ²

неизвестные функции, тогда

где Я находится из характеристического уравнения sin( Я ) = 0.

Вычислим вначале

8 T ( X , 0 ) .

8 X   *

8 T ( X ,0)    .                           .

--—— = ^{- 1 - 2} L ^{( - 1)} p COs [ ⁽l ^{- X)} п p ^] X

8 X            p = i

_ 2 _2

^X exp^{( - 0} —p )■

Pr

Запишем уравнение (8) в виде:

—¹ Я

80 I ^X

"8 ²Ф~| _ Гд²Ф H _

^{+ Tx} dF Г^Tx

L 8 X J     L 8 1 J

8 ⁴ Ф

J X ⁴ _

+

⁺ J"x

2       ' !

8 X ² 8 У²

⁺ X_x

8 ⁴ Ф     Г8 Г

8 У ⁴ J ^X Ld X

Идентифицируем преобразования в (17):

T

X

8 ² Ф

8 X 2

1 8 ² Ф ( X , У , 0 )

J     8X²

sin( Я X ) dX =

-Я Ф^⁸^

X   8 Y ²

= Я cos Я + A + Я В + Я⁴Ф_х -

2 8 ² Ф x    8 ⁴ Ф x   1г    . _п

2 Я         I ( cos Я - 1 ) +

8 У ²     8 У ⁴ Я^{v        !}

да

+2^(-1) p p=1

Я L cos Я - cos ( n p ) J

п ² p ² - Я²

_ 2 „2

exp[ - 0 -p ], Pr

Ф x ( Я , Y ,0 ) = 0, Ф_Х ( Я ,О, 0 ) = Ф_Х ( Я ,1, 0 ) = 0, 8Ф x ( Я ,0, 0 )_ 5Ф x ( Я ,1, 0 )^_о

8 Y

8 Y

Вычислим синус трансформанту по переменной Y

Ф xy = Л ГФ x ( Я , Y , 0 ) J =

1                                              (20)

= J Ф x ( Я , Y, 0 ) sin ( цY ) dY = Ф xy ( Я , ^ , 0 ) , где , находится из характеристического уравнения sin ( ^ ) = 0. Тогда (19) примет вид

= - Я ² Ф x ; _ Г8²Ф"

I

— \-ЯХ к ф, +к YX  Y

8 ² Ф

X

X

8 ²       .               ,

, =—?Х[Ф ( X, Y ,0) ] = дг2    ar2 XL          J

82Ф,.

8 У² ’

Г 8 Y²

= - Я cos Я ,[ A ] + Я ,[ B ] + ЯХ х[Ф_х]-    (21)

8 ⁴ Ф

8 X ⁴

= - Я cos Я

1 8 ⁴ Ф ( X , У , 0 ) .

= J---^---sin( Я X ) dX =

- 2 ЯХ_У

8 ² Ф

8 ⁴ Ф

- 4

8 ² Ф (1, У , 0 ) 8X²

- 8 ² Ф (0, У , 0 ) .л

+ Я---  ,   + Я Ф _у;

8Х ^{2          x}

8 ⁴ Ф 8 X² 8 У²

2 81 у ⁸1Ф

8 У^{2  x} Г 8 X²

= - 2 Я²

8 ² Ф x 8У² ’

8 ⁴ Ф 1_84_ _{т [ф]}   8 ⁴ Ф X ( Я , У , 0 ) .

8 У ⁴ J   8 У⁴   X           8 У⁴     ’

I        ж^

|^ - 1 - 2 V ( - 1) ^p cos[(1 - X ^ p ]exp( - 0—p -)

•0 1         p = 1                                            ^Pr

• sin( Я X ) dX = - ( cos Я - 1 ) - Я

.'I ( - 1) p     Я - “^ p ^)] exp( - 0 ^).

p = 1         n p - Я            Pr

- Ту [ T x ] .

Г 8 Y² _             .

Идентифицируем преобразования в (21):

_ 8 Y'

Y

8 ² Ф

г 8 Y²

¹ 8 ² Ф

= J -ГХ- ^sin( ^ ^Y ) ^dY = ^- ^ ^Ф XY \

0 ^{8 1}

X , [ A ] = A Y ( ^ , 0 );   X_Y [ B ] = B Y ( ^ , 0 );

Y

"8 ⁴ Ф, г 8 Y⁴

1 8 ⁴ Ф г .

= J -^^ ^sin( 0 Y ) ^dY =

0 ^{8 1}

8 ² Ф_Х( Я ,1, 0 )    8 ²Ф_У( Я ,0, 0 )

-и cos и ----^--- + и ----^---- +

8 X ²            8 X ²

⁺ Ц ^Ф XY ;

т =тЛт г XY Y Y V X

да

- 2 ^ ( - 1) ^p

8 T

8 X

[I — ( cos Я - 1 )-

J Я

Я [cos Я - cos( n p )]

p = 1

x sin( ^ Y ) dY =

да

= -2 ^ (-1)

p = 1

п ² p ² - Я²

п ² p ² I exp(- 0 ——) >  x Pr

_p Я [cos Я - cos( n p )]

п²p ² - Я²

- 2   2  ]

^exp( - ⁰ -PT) •■

Обозначим через d2Ф. (X,1,9)      d2Фх (X,0,9)

=----X^,2 ), d =----X ( , , )(22)

SY2

неизвестные функции, тогда:

^^Y + (X2 + д2 )Ф.¥У= -X   Xcos XAy d9              XY  X2 + д21

—XBy + д cos дС — дD ] — Tyx , Ф XY ( X , д ,0 ) = 0.

-

Интегралы типа (27) в каждый момент времени 9 представляют собой постоянные и находятся путем решения системы линейных уравнений, полученной из граничного условия на частные производные функции (14):

Анализ результатов

На рисунках 2–5 изображены карты функции тока, компоненты скорости v и v , и поля скоростей для числа Прандтля Pr=1 в разное время: а) 9 = 0.001 , б) 9 = 0.01 , в) 9 = 0.1 , г) 9 = 1 .

Решив уравнение (23) с начальным условием (24), получим для изображения:

Ф_Л) = exp ^- 9 ( X ² + д ²) ] j^p---- 2 X cos XA_y -

-XB_Y + д cos д С - д D -

- Txy exp ^- z ( X ² + д ²) ] dz .

Выражение для функции тока получим последовательным применением обратных преобразований Фурье:

Ф(X,Y,9) = 4££фxy (Xn,д,9)x n=1 m=1                       (26)

X sin ( X n X ) sin ( Ц m ^Y ) ,

где X _n = n n и д _т = n m .

В решение (26) входят интегралы от неизвестных функций (18) и (22), для вычисления которых предположим, что справедливо:

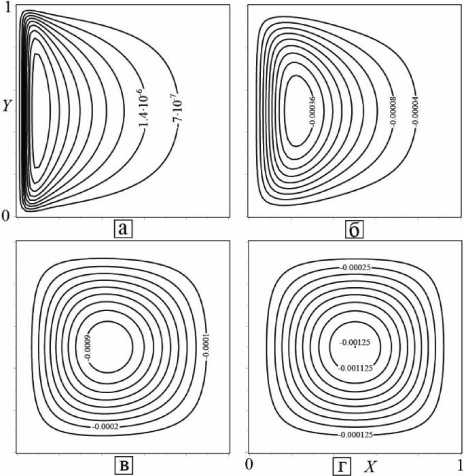
Рисунок 2. Карты функции тока

Figure 2. Flow function map

j A_Y ( д , z )exp[ z (X² + д ²)] dz =

= А( д , 9 ) j exp[ z ( X + д ²)] dz , 0

При данном допущении, выражение для изображения примет вид

X

cos д - 1

П ^X , д,⁹^-- --^^X

’ № + д ²)

(cos X - 1) {1 — exp [ - 9 ( Л ² + д ²) ] }

X ( X + д ²)

+

X

«                              (28)

+2PrX^(-1)p [cos X - cos(np)]x p=1

2   2                                     1

^{exp^{( - 9} ——)^- exp^{[ - 9 (} Я ² + д ^2)]}

Pr

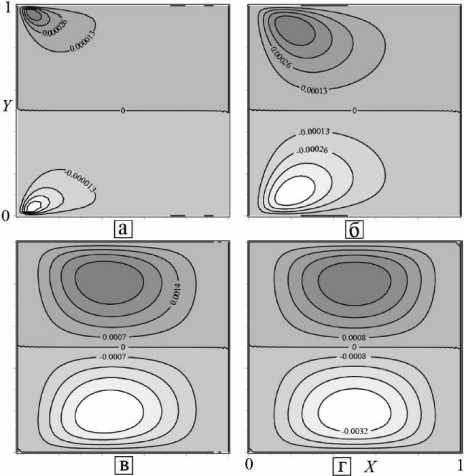
Рисунок 3. Карты компоненты скорости v

( n ² p ² - X ²) [ n²p ² - Pr( X ² + д ²) ]

Figure 3 .Velocity component v maps

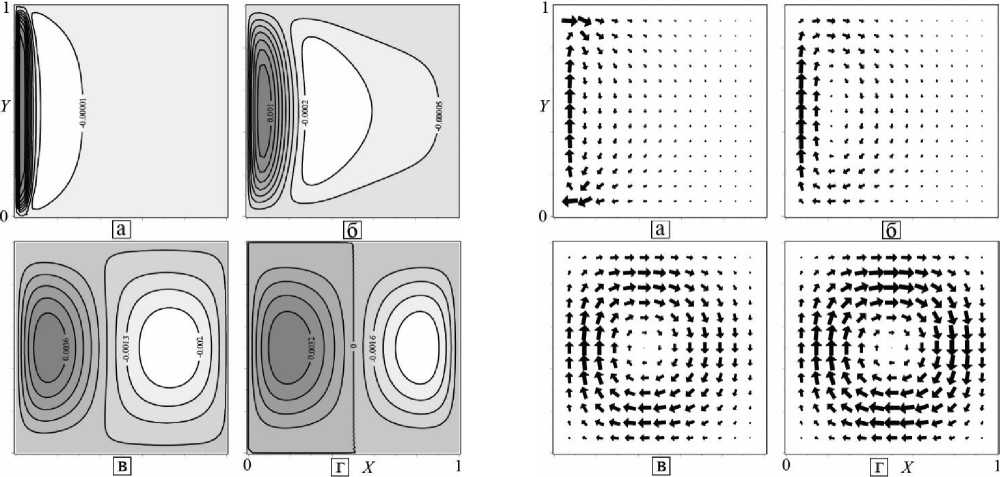
Рисунок 5. Поле скоростей

Рисунок 4. Карты компоненты скорости v

• Figure 4.    Velocity component v maps

Течение начинается возле нагретой стенки (рисунок 5 а) и распространяется к холодной(рисунок 5 б и в).

При переходе в стационарное состояние (рисунок 5 г) образуется единственный вихрь, закрученный по часовой стрелке с неподвижной точкой в центре области.

• Figure 5.    Field of velocities

Достоверность гипотезы о специальном виде интегральных коэффициентов подтверждается адекватностью физическому смыслу и согласованностью полученных результатов с представленным решением задачи [9].