Приближенные аналитические решения LPlm мод для частных примеров профиля показателя преломления оптического волокна
Автор: Бурдин Антон Владимирович, Бурдин Владимир Александрович, Дельмухаметов Олег Равилевич, Яблочкин Константин Александрович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии телекоммуникаций
Статья в выпуске: 1 т.9, 2011 года.
Бесплатный доступ
Представлены приближенные аналитические решения для направляемых линейно-поляризованных LPlm мод круглого оптического волокна (ОВ) для частных примеров профиля показателя преломления. Приведены результаты вычислений на основе полученных формул оценок параметров мод для исследуемых примеров.
Оптическое волокно, линейно- поляризованные моды, профиль показателя преломления, эквивалентный радиус пятна моды
Короткий адрес: https://sciup.org/140191446
IDR: 140191446 | УДК: 621.315
Текст научной статьи Приближенные аналитические решения LPlm мод для частных примеров профиля показателя преломления оптического волокна
Одним из эффективных методов решения задачи для круглого слабонаправляющего оптического волокна является метод приближения Гаусса, в основе которого лежит аппроксимация поля моды ОВ с произвольным профилем показателя преломления полем моды ОВ с неограниченным параболическим профилем [2-6]. Данный метод достаточно хорошо известен и подробно описан [2-4]. В работах [2-6] представлены полученные данным методом приближенные аналитические решения для основной моды для частных примеров профиля - ступенчатого, сглаженного степенного, описываемого функцией Гаусса. В [5-6] предложена модификация метода приближения Гаусса, позволившая за счет применения совместно с ним метода стратификации [7-8] получить приближенные решения для мод сла- бонаправляющего круглого оптического волокна с профилем произвольной формы. При этом стратификация профиля вносит дополнительные погрешности. В данной работе представлены полученные на основе приближения Гаусса аналитические решения для частных примеров профилей показателя преломления для направляемых линейно-поляризованных LPlm мод произвольного порядка. Данные решения могут быть использованы для анализа, в качестве тестовых примеров, для оценки погрешностей и т.п.
Общее решение. Основы метода приближения Гаусса
Рассмотрим метод приближения Гаусса подробнее [3]. Предполагается, что продольные составляющие полей линейно поляризованных мод LPlm слабонаправляющего ОВ в цилиндрических координатах записываются в виде гармонических функций:
^exp[-y(^ -Д
E- = Г(/|(гК "^
, [cos/^
где R = r/a – радиальное распределение поля моды LPlm ; l и m – азимутальный и радиальный порядок моды LPlm соответственно; P – постоянная распространения. При этом радиальная зависимость поля моды f^\r^ некоторого ОВ описывается выражением:
VR0
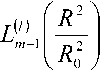
exp
2^Г>
где R = r/a – нормированный радиус; r – коорди- ната; a – радиус сердцевины волоконного световода; R0 = r0 /a – нормированный радиус пятна моды; r0 – радиус пятна моды; ^т-\ – полином Лагерра.
Задача сводится к определению некоторого эквивалентного радиуса пятна моды R 0 для заданного ОВ. Найденный параметр является для данного приближения базовым и полностью определяет искомые характеристики моды. Для слабонаправляющих волокон ^т (^) является решением дифференциального уравнения:
Вычисление интегралов, не зависящих от профиля показателя преломления ОВ
Рассмотрим подробнее составляющую ^АкУ . Сделаем замену переменных: x = R2/ R^ и п = т-1 . Тогда из (1) следует
№-Ш-. (9)
С учетом этого интеграл (5) после замены переменных принимает вид:
^ =а ^ jv^x)]^-^.
С учетом свойства ортогональности полиномов Лагерра [8-9]:
fL^i-^'-^J^.p dr' г dr г
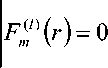
из которого следует выражение для постоянной распространения моды [3]:
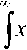
1 е ' р рУ„ ^dx = <
получаем:
п\
О
к = и;
к * и.
(Ю)
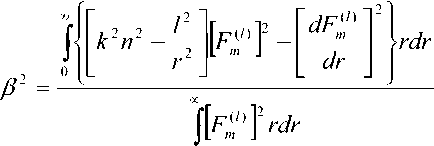
о
Перепишем его в виде:
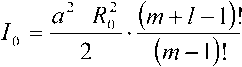
Свойство полиномов Лагерра [3; 5]:
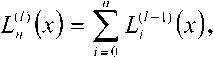
(И)
Р' = 4*^11,ктУЧ'^кт), ^аУ1,У = 1х1 Р, ^(/,^) = (/3-/2)//0,
Zo = jk0^)]2^, О
^ = j^TT^^'Cr)]'/^-,
/2 = |—^(г)]2/-^, о ‘
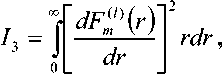
позволяет интеграл (7) после замены перемен-
ных представить в виде:
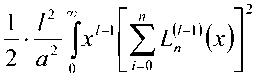
е ' dx.
Отсюда, с учетом (10), получаем
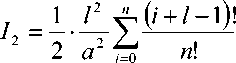
где n ( r ) – профиль показателя преломления ОВ.
Эквивалентный радиус пятна моды находят как решение уравнения др2 /дг0 = 0.
Описанный подход требует аналитического решения задачи и вывода уравнения пятна моды для каждого частного примера формы профиля показателя преломления.
Производную функции ^т будем искать, учитывая, что dY2 / dx = 2У • dY / dx . Предварительно, используя свойства полиномов Лагерра [9-10]:
xdPp ^1 dx = nLp (x) - (и + / ^P’P (x), (14) xLT МЦп + lX"n M - (и +1 )L(„,;11) (x), (! 5)
находим производную:
у- V1^ (хУх ]=(«+O^-1 ^„-i0 (*)e“% ■ dx
Производную
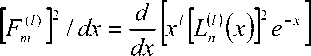
запишем в виде
^4° M^ ]+1'^0 UK' "\-p-K K\ dx dx
Тогда, с учетом (14)-(15), получаем
^H1^)]’^fm z =xp(--v)
Z = («+1)C* M+<■" M - C, ■
Производная dF^ / dx равна:
А = jE^F^/V)]"^-О '=°
Сделав замену переменных, интегрируя и группируя слагаемые, получаем
„2 п2 Г Д' )
/,=^F»M(o)+1Fa«M(x,) •
Здесь
■FF)- JH'wNv,
A F1 K4 к-' <Л)Г' F™'w * dx2 dx или — Fj/^T?) = — x2
dx2
Поскольку ^LF^(r) = -EF^^~, to dr dxdr
I3 = — ^x1”'Z2e”xdx.(16)
Интегрируя (16) согласно (10) и с учетом
(14)-(15), получаем:
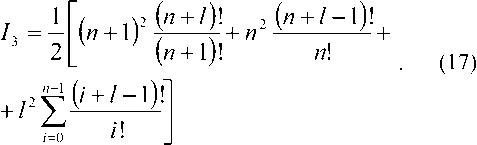
A/F =/F-^i-
Значение ф^(о) определяется согласно (10), а ^0 – значение показателя преломления на оси ОВ. Отсюда следует
/77!
E^2a«,2o(f) •
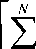
2 >2 .2 _ /=1
И соответственно 2^Ф^\х^ (22)
(m + /-l)!/(/77-l)!
Дифференцируя (22) no r0 с учетом
A®M=[F’M]2
dx и приравнивая производную нулю др11 drti = 0, получаем уравнение для эквивалентного радиуса пятна моды в виде:
Окончательно получаем:
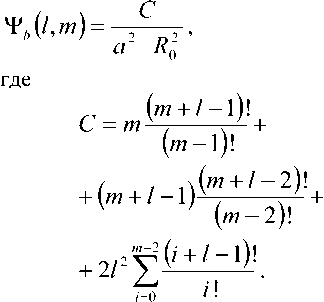
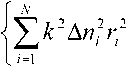
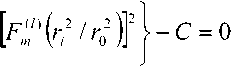
где C – константа для заданного порядка моды l , m .
Общие выражения для постоянной распространения и уравнения эквивалентного радиуса пятна моды для произвольного профиля
Если в (23) число слоев устремить к бесконечности, то сумму можно представить как интеграл
Уравнение эквивалентного радиусапятна моды
Для определения ^(,7,/,/??) воспользуемся методом стратификации [6-7] и, как и в [4-5], некоторый заданный произвольный профиль показателя преломления будем аппроксимировать многослойным. Это позволяет интеграл (6) представить в виде
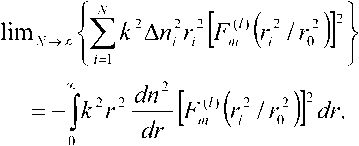
Тогда в общем случае выражение для постоянной распространения (2) и уравнение эквивалентного радиуса пятна моды (23) запишутся как
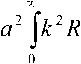
^Пфк^^^ (25)
dR
x4 cx^{px)dx =
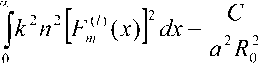
(т + 1 — l)!/(m -1)!
Аналитические решения для частных примеров профиля показателя преломления. Ступенчатый профиль показателя преломления
Ступенчатый профиль показателя преломления описывается формулой [3]:
n(R) =
^C
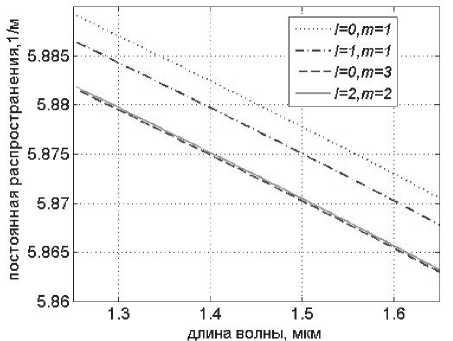
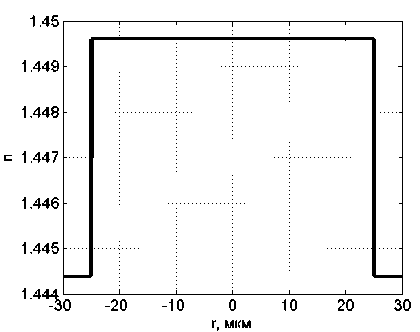
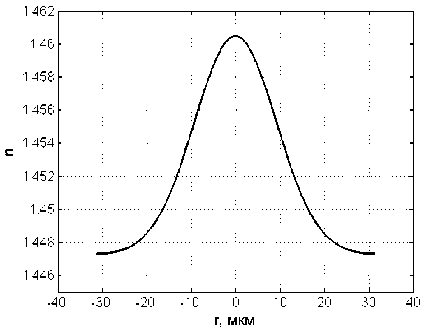
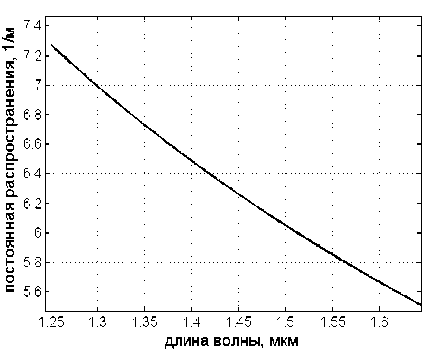
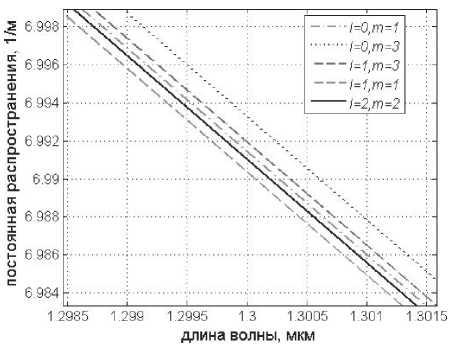
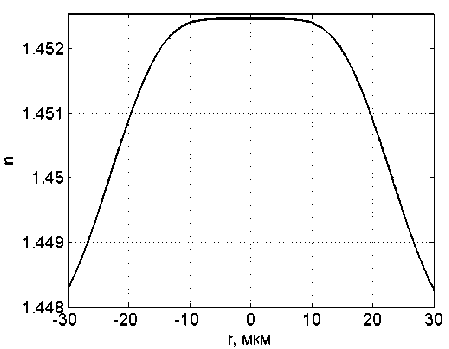
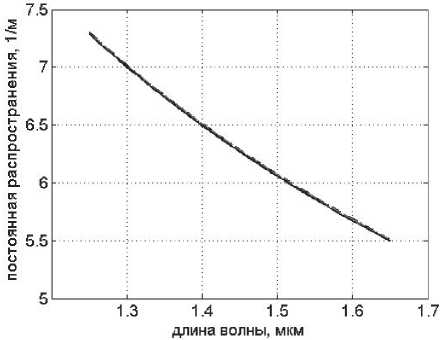
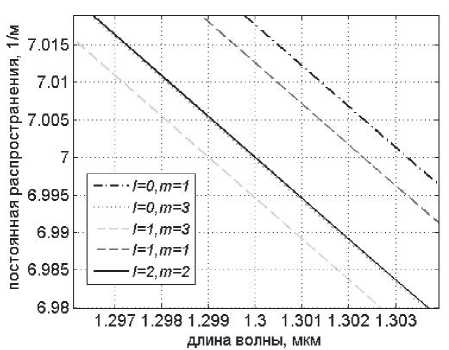
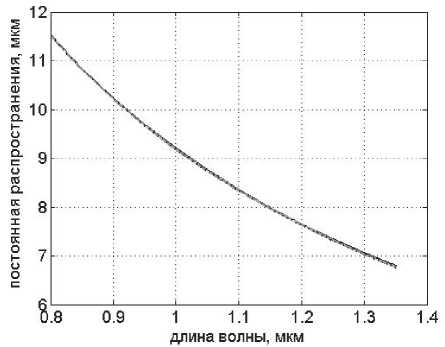
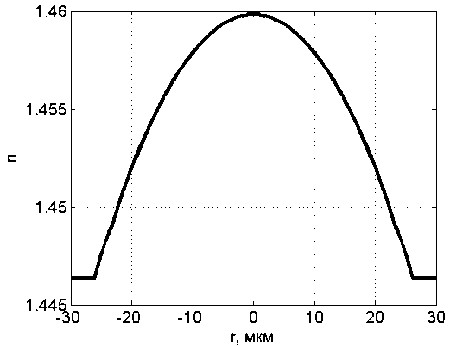
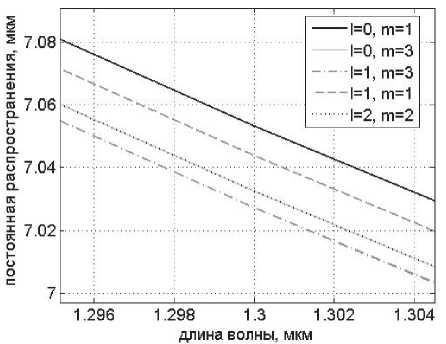
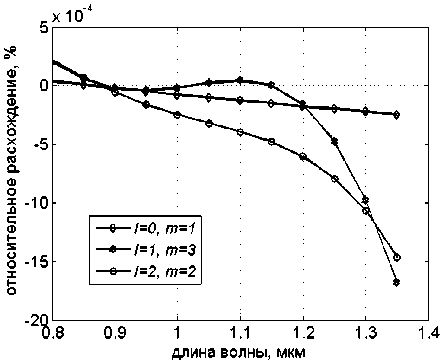
R R>RS’ где n№ nc – показатели преломления сердцевины и оболочки ОВ соответственно; Rs – относительное расстояние от оси ОВ до границы с оболочкой. Подставляя (24) в (25), получаем уравнение эквивалентного пятна моды для ступенчатого ОВ: a-k^n-R] гдеАй2= Hq -H^. Выражение для постоянной распространения принимает вид: к^Ф^ p2 = k2n2----- ^1 R») Для вычисления функции воспользуемся формулой для обобщенных полиномов Лагерра [8-9]: ЭД=Й'< 6(/) , 4 qX^n-qX^qY fc''M] =Ы'-Л g^t^-C /=0 Известно, что [9] = exppv Pk4q-k\ Учитывая это, получаем где ф«^=оГ^А G,i'")(,v,6) = exp(-fa) ^g® ^ G + a) ! xw"k + ^(q + p-k)\ bk+x хч+ц b (33) На рис. 1 приведены примеры спектральных зависимостей постоянных распространения отдельных мод ступенчатого ОВ c оболочкой из чистого кварцевого стекла, радиусом сердцевины a = 25 мкм и высотой профиля 0,36%. Профиль показателя преломления данного ОВ представлен на рис. 2. Рис. 1. Спектральные зависимости постоянных распространения отдельных мод ОВ со ступенчатым профилем Рис. 2. Пример ступенчатого профиля ОВ Профиль показателя преломления, описываемый функцией Гаусса Гауссов профиль показателя преломления волокна описывается формулой n2 (R) = n2c + ^ - nG )exp(- R2 /Rq ), (34) где ^0’ ^c – показатели преломления в центре сердцевины ОВ и оболочки ОВ соответственно; ^G – безразмерный параметр Гауссова профиля. Подставляя (28) в (29) и сделав замену переменных x = R2 /Ro иn = m — X, запишем (25) с учетом (9) в виде: C - a2k2^2Rq p ■ IG =0, (35) где /G = Jx,+Vfa[zdd)]X « (36) p = R2 ! R2; b = X* p. Известно, что [9]: PPHnFF?VY (37) тогда [4Z)^)]2 = t^/ "f Cv)]2 + [z^p Cd]2 - (38) -lp"Wp Это позволяет свести (33) к сумме трех интегралов, каждый из которых в общем виде можно представить как Это табличный интеграл. Согласно [10]: [x'^L'paPL'pa^^ (^ + Z22 + //) × ^l^! Здесь F[t/,v;c;z] – гипергеометрическая фун- кция. Отсюда следует ■ nx'.n2’b c = r^ + n2 + p-X, b(b-2) (6-l)2 Поскольку в рассматриваемом случае, по крайней мере, один из аргументов гипергеометрической функции f[k,v;c;z] – целое отрицательное число, она может быть вычислена как конечная сумма по формуле [9]: FV-nA-np-c;z^^---.—----. (41) С учетом (31)-(35) получаем: ^=Bt:wBpUbV2CW). (42) Подстановка (39) в (32) дает уравнение эквивалентного радиуса пятна моды для Гауссова профиля. С другой стороны, если представить в (36) полином Лагерра во второй степени согласно (30), (31) и воспользоваться формулой (32), то согласно (33) получаем io =о»'*'Ч»,ьу Для нахождения постоянной распространения подставим (28) в (6). После замены переменных x = R” /R^ и n = m-X получаем /, -k2^2^- Р'е^^М]2^- Тогда, согласно (2)-(6), (26) и (30)-(33), выражение для постоянной распространения моды ОВ с Гауссовым профилем показателя преломления принимает вид к2 ^2 R2G\kl\0,b^-(43) P2 = k2n2 +----?. (m +1 - 1)!/(;m -1)! На рис. 3 представлен пример Гауссова профиля показателя преломления ОВ при Rpj 0)5. На рис. 4 представлены результаты вычислений спектральных характеристик отдельных мод для этого профиля, а на рис. 5 эти же характеристики, но в увеличенном масштабе для длин волн в области 1,3 мкм. Рис. 3. Пример профиля показателя преломления ОВ, описываемого функцией Гаусса при Rg = 0,5 Рис. 4. Спектральные зависимости постоянной распространения отдельных мод ОВ с Гауссовым профилем показателя преломления Рис. 5. Спектральные зависимости постоянной распространения отдельных мод ОВ с Гауссовым профилем показателя преломления Сглаженный степенной профиль показателя преломления Сглаженный профиль показателя преломления описывается выражением [3]: или, после интегрирования по частям: nXRW, 1-2Ае-'^ , y^uR1; и-р + 1; А = (иц - и2 )/(2nJ ), где р – натуральное число или ноль. При р = О– это Гауссов профиль, а при р = оо – ступенчатый. При R«1 выражение (40) принимает вид как для степенного профиля [3]. Дифференцируя (44) и подставляя в (25), по- сле замены получаем уравнение: к3 \п2 a3uRq + С = 0, где b = 1 + uRq . И окончательно, учитывая (30)(33), для сглаженного профиля получаем уравнение эквивалентного радиуса пятна моды в следующем виде: кг\па2иРп „ —.----7-^g\*-*р\ь,^- с = о. (46) (»-!)! Чтобы получить выражение для постоянной распространения, воспользуемся формулой (45). Подставляя ее в (26), после замены переменных получаем: Отсюда, согласно (30)-(33), следует: На рис. 6 приведен пример сглаженного профиля для р = 2 . На рис. 7 приведены спектральные зависимости постоянных распространения отдельных мод, рассчитанные для этого профиля по формулам (46), (47). На рис. 8 приведены эти же зависимости в увеличенном масштабе для длин волн в области 1,3 мкм. Ограниченный параболический профиль показателя преломления Для описания ограниченного параболического профиля показателя преломления волокна воспользуемся выражением [3]: л02(1-2А7?2) ,0 Подставляя (40) в (29), после дифференцирования и замены переменных x = R2/R", и п = т-1 получаем интеграл (26) в виде - а2к2^п2Рц Jx[Fn(/*(х)]’dx, о где Хр = Rp / Rq . Или с учетом (9): — a^k2^n"R4} jx/+1e l[z^’(x)] dx. (49) о Рис. 6. Пример сглаженного профиля показателя преломления ОВ при p = 2 Рис. 7. Спектральные зависимости постоянной распространения отдельных мод ОВ с Гауссовым профилем показателя преломления Интегрируя (49) согласно (30)-(33) и подставляя результат в (26), получаем уравнение для эквивалентного радиуса пятна моды ОВ с усеченным параболическим профилем: a2k2An2R40[g,(//+1)(1,0)- G^’O^J- C = 0. Подставляя (40) в (6) и интегрируя, с учетом (41)-(48), из (2)-(6) получаем аналитическое выражение для постоянной распространения направляемой моды ОВ с ограниченным параболическим профилем Рис. 8. Спектральные зависимости постоянной распространения отдельных мод ОВ с Гауссовым профилем показателя преломления Рис. 10. Спектральные зависимости постоянной распространения отдельных мод ОВ с ограниченным параболическим профилем На рис. 9 приведен пример ограниченного параболического профиля показателя преломления ОВ. На рис. 10 представлены спектральные зависимости постоянных распространения отдельных мод, рассчитанные по формулам (49)-(50). Рис. 9. Пример ограниченного параболического профиля показателя преломления ОВ На рис. 11 приведены эти же зависимости в области длины волны 1,3 мкм. На рис. 12 представлены кривые, характеризующие относительное расхождение результатов расчетов с оценками, полученными численным методом – методом смешанных конечных элементов [14-15], алгоритм реализации которого подробно описан в работе [16]. Данные достаточно хорошо согласуются – расхождение не превышает 0,002%. Рис. 11. Спектральные зависимости постоянной распространения отдельных мод ОВ с ограниченным параболическим профилем Рис. 12. Относительное расхождение оценок постоянных распространения мод, вычисленных по аналитическим формулам (49-50) и численным методом для рассматриваемого примера параболического профиля Заключение В работе получены приближенные аналитические решения для направляемых линейно-поляризованных мод для частных примеров профиля показателя преломления ОВ: ступенчатого, Гауссова, сглаженного степенного, ограниченного параболического. Выведены уравнения эквивалентного радиуса пятна моды и выражения для постоянной распространения. Для исследуемых профилей приведены оценки спектральных зависимостей постоянных распространения отдельных мод, вычисленные по полученным формулам. Сравнение результатов вычислений с оценками, полученными численным методом (методом смешанных конечных элементов), для примера ОВ с ограниченным параболическим профилем показало, что они достаточно хорошо согласованы – расхождение не превышало 0,002%.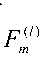
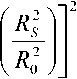
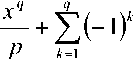
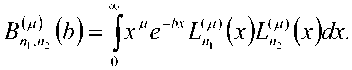
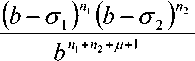
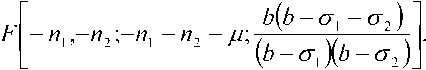
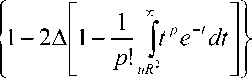
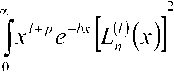
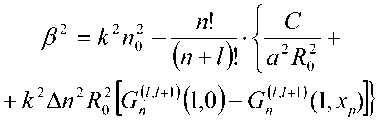
Список литературы Приближенные аналитические решения LPlm мод для частных примеров профиля показателя преломления оптического волокна
- Snyder A.W. Understanding monomode optical fibres//Proceedings IEEE. V. 69, № 1, 1981. -P. 6-13.
- Love J.D., Hussey C.D. Variational approximations for higher-order modes of weakly-guiding fibers//Optical and Quantum Electronics. V. 16, N1, 1984. -P. 41-48.
- Снайдер А., Лав Дж. Теория оптических волноводов. М.: Радио и связь, 1987. -656 с.
- Бурдин В.А. Основы моделирования кусочно-регулярных волоконно-оптических линий передачи сетей связи. М.: Радио и связь, 2002. -312 с.
- Андреев В.А., Бурдин А.В. Многомодовые оптические волокна. Теория и приложения на высокоскоростных сетях связи. М.: Радио и связь, 2004. -248 с.
- Clarricoats P.J.B., Chan K.B. Electromagnetic-wave propagation along radially inhomogeneous dielectric cylinders//Electron. Letters. V. 6, № 22, 1970. -P. 694-695.
- Arnold J.M. Stratification method in the numerical analysis of optical waveguide transmission parameters//Electron. Letters. V. 13, № 22, 1977. -P. 660-661.
- Абрамовиц М., Стиган И. Справочник по специальным функциям. М.: Наука, 1979. -830 с.
- Градштейн И., Рыжик И. Таблицы интегралов. М.: Физматгиз, 1962. -1100 с.
- Shen J. Stable and efficient spectral method in unbound domains using Laguerre functions//SIAM J. Numer. Anal. V. 38, № 4, 2000. -P. 1113-1133.
- Funaro D. Computational aspects of pseudospectral Laguerre approximations//Appl. Numer. Math. № 6, 1990. -P. 447-457.
- Pon-Aun Lee, Seng-Huat Ong, Srivastava H.M. Some integrals of the products of Laguerre polynomials//Intern.I.Computer Math. V. 78, 2001. -P. 303-321.
- Бурдин А.В., Яблочкин К.А. Исследование дефектов профиля показателя преломления многомодовых оптических волокон кабелей связи//ИКТ. Т. 8, № 2, 2010. -C. 22-27.
- Боголюбов А.Н., Делицын А.Л. Расчет диэлектрических волноводов методом конечных элементов, исключающий появление нефизических решений//Вестник МГУ. Сер. 3. Физика. Астрономия. № 1, 1996. -C. 9-13.
- Koshiba M., Maruyama S., Hirayama K. A vector finite element method with the high-order mixed interpolation-type triangular elements for optical wave-guiding problems//J. Lightwave Techn. V. 2, № 3, 1994. -P. 495-502.
- Бурдин В.А., Бурдин А.В., Султанов А.Х., Дельмухаметов О.Р. Алгоритм расчета хроматической дисперсии одномодовых ОВ на основе метода смешанных конечных элементов//ИКТ. Т. 7, № 2, 2009. -С. 13-16.


