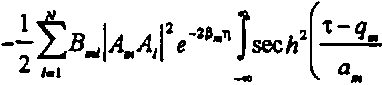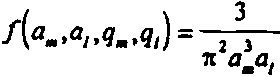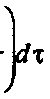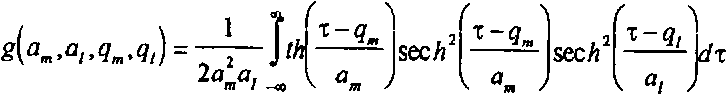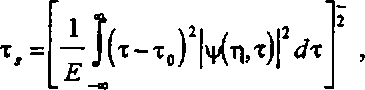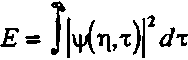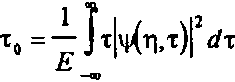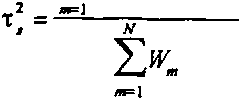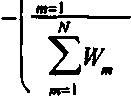Приближенные параметрические модели динамики самовоздействия импульсов в нелинейных оптических средах с модовой дисперсией

Возрастающий интерес к анализу процессов самовоздействия импульсов когерентного излучения в нелинейных оптических средах связан с возможностями их использования для получения импульсов особо малой (фемтосекундной) длительности, повышения скоростей передачи информации по волоконно-оптическим каналам, создания различных новых оптических приборов, элементов оптической обработки информации со сверхвысоким быстродействием, а в перспективе - оптических компьютеров [1-9]. Доказана возможность самостабилизации импульсов и образования солитонов не только в одномодовых, но и в многомодовых оптических волокнах [2, 10, 11]. Хотя для создания высокоскоростных систем дальней оптической связи многомодовые волокна мало пригодны (главным образом потому, что из-за большого диаметра сердцевины для получения в них солитонных режимов требуются мощности на несколько порядков выше, чем в одномодовых волокнах), во многих других нелинейных оптических системах необходимо принимать во внимание модовую дисперсию. В первую очередь это относится к различным устройствам оптической обработки информации [12, 13]. Кроме того, и в одномодовых световодах при технологических нарушениях симметрии сечения волокна и неоднородностях появляются различия постоянных распространения двух ортогонально поляризованных мод (двойное лучепреломление), приводящие к модовой дисперсии [14]. Сходные з ад ачи (но уже для разных частот, а не постоянных распространения) возникают при анализе вынужденного комбинационного рассеяния, которое предполагается использовать для компенсации потерь в волокне и увеличения дальности солитонных систем оптической связи [3, 4, 9].

Основу для решения задач анализа и расчета указанных оптических систем и устройств дает общая теория нелинейной динамики интенсивных сверхкоротких импульсов в многомодовых световодах, развитая в последние годы [15-17]. В общем случае уравнения эволюции модовых компонент импульса оказываются сложными и не допускают аналитического решения. Однако в большинстве практических задач расчета оптических систем (в частности, волоконно-оптических систем связи и устройств обработки информации в цифровой форме) нет необходимости в детальном анализе эволюции формы импульсов, достаточно знать характер изменения их отдельных параметров. В таких случаях анализ динамики самовоздействия может быть выполнен на основе гораздо более простых параметрических моделей, некоторые из которых рассматриваются ниже.

• 1.    Нелинейные уравнения эволюции импульсов в многомодовом световоде

В общем случае такие уравнения должны быть записаны в векторной форме и требуют учета изменений поперечной структуры поля [15-17]. Если, однако, ограничиваться учетом только тех нелинейных явлений, которые связаны с зависимостью показателя преломления от интенсивности поля, и при этом не учитывать инерционность его нелинейной части, а также ряд других нелинейных эффектов, в том числе дисперсию выше второго порядка, то можно использовать скалярные модели, в которых взаимосвязь мод определяется только зависимостью показателя преломления от их суммарной интенсивности [10]. Такие упрощенные модели достаточно хорошо описывают динамику самовоздействия небольшого числа мод (наиболее точно - двух мод [17]).

При указанных условиях и обычных допущениях метода медленно меняющихся амплитуд процесс распространения импульса когерентного излучения в регулярном световоде с кубической нелинейностью поляризации описывается системой уравнений шредингеровского типа для N взаимосвязанных ортогональных мод [10]

Эш du/ о w           Xs I I2 л i^+n'„^+“„^+'fi..V„ + LK-/H *.=o an дт ox            /=1

(т=и,...,Ю где n=z/£ , t=(/-Vvo)/7o " продольная пространственная и смещенная временная координаты”’нормированные с некоторыми масштабами по длине z(Z0), времени 1(1^ и скорости (v0); - комплексная огибающая импульса m-ой моды, нормированная на ее максимальное по модулю значение на входе световода (^0), am’ Рт’ Ут» Кт1

коэффициенты, характеризующие дисперсию, затухание, относительную скорость взаимного смещения и нелинейность по каждой моде и определяемые выражениями

ТГ_й dw

L=hL' 1т= —

• т т м • т гр

1 1

к*/ — к„(Е0 j-S^,

к„(£о)

^0^0^2 ^0^0

Здесь v_m, Л_т, р_т - групповая скорость, коэффициент затухания и постоянная распространения m-ой моды (в размерных единицах), В_т, В^ - коэффициенты, определяемые в результате усреднения m-ой и Z-ой мод по формулам, приведенным в [2], л_о, П2 - невозмущенное значение показателя преломления и коэффициент в его нелинейном члене.

При описании одномодового режима (N=Y) обычно выбирают в качестве L_o "дисперсионную длину" L^, соответствующую удвоению ширины импульса в линейном режиме, в качествее Т_о - его начальную полуширину, v_o - групповую скорость волн. Тогда в эволюционном уравнении у=0, а=1 [2]. Для системы нескольких уравнений вида (1) выполнить такое масштабирование в общем случае невозможно (хотя для двух мод можно учесть различие в скоростях с помощью дополнительных фазовых множителей, а в уравнениях положить у₁=у₂⁼® U ID-

Система уравнений (1) описывает процесс распространения импульса в световоде при начальных условиях hVM = VmoW, т= 1,2,-Л; (3) где ц/гпо(т) - комплексные огибающие импульсов, возбуждаемых на входе световода по отдельным модам.

К аналогичному виду приводятся уравнения динамики двухчастотного взаимодействия импульсов [7], а также импульсов в волокнах с двойным лучепреломлением (с тем отличием, что перекрестные члены уравнений содержат и линейные слагаемые) [14].

Точное аналитическое решение уравнений вида (1) затруднено, а численное решение требует больших затрат машинного времени. Однако в большинстве технических задач, связанных с расчетом нелинейных оптических элементов систем обработки и передачи информации, знание полной картины эволюции импульсов, обеспечиваемое такими решениями, как уже отмечено выше, не требуется, достаточно знать некоторые общие параметры импульсных сигналов. Уравнения их эволюции могут быть выведены из исходных уравнений (1) на основе автомодельных приближений, рассматриваемых ниже.

Автомодельные решения эволюционных уравнений

Импульсы \ит(т|/с) , являющиеся автомодельными решениями уравнений (1), обладают свойством сохранять свою форму неизменной в процессе распространения по волокну, т.е. при всех значениях и . Получение такого решения позволяет свести задачу анализа преобразования импульса к определению эволюции его параметров.

Существует два частных вида уравнений (1), для которых известны точные решения такого рода. В линейном режиме, когда все кт1=0, система (1) распадается на N не связанных между собой линейных уравнений отдельных мод, для каждого из которых при начальном воздействии (3) гауссовской формы решение также имеет вид гауссовского импульса с измененными параметрами. Второй частный случай - одномерное (Л^О нелинейное уравнение Шредингера (НУШ), в котором 0=0, а а и к имеют критические значения, соответствующие распространению солитона (например, а=1 и к=2). Последний, как известно, имеет форму гиперболического секанса и без изменения этой формы распространяется по волокну.

В остальных режимах импульсы указанного вида можно рассматривать лишь как некоторые естественные приближения к точному решению уравнений (1). В [18] получено и исследовано автомодельное решение гауссовской формы для одномерного НУШ. Показано, что такое приближение дает в целом правильную качественную картину эволюции импульса, позволяет выявить ее основные режимы и рассчитать изменения параметров. В [19] эти результаты обобщены на многомодовые световоды, описываемые системами НУШ вида (1).

Однако, естественно ожидать, что для нелинейных режимов, близких к солитонному, более точным окажется автомодельное приближение в форме гиперболических секансов. Рассмотрим такое решение для системы НУШ (1) и сравним его с гауссовским приближением.

Пусть на входе световода, описываемого уравнениями (1), действует импульс когерентного излучения, комплексные огибающие которого по отдельным модам имеют вид

Ущо^АпоД^ а^хр^т; ^mo> cmo)l (4)

где - начальная комплексная амплитуда импульса m-ой моды,

V°nO /

- модуль его нормированной огибающей,

®(т> ^mo’ сто) ^то^+^то1

- начальная фаза.

Здесь ато, /?то, сто - начальные значения полуширины, коэффициенты линейной частотной модуляции (ЛЧМ) и сдвига средней частоты импульса m-ой моды (при одночастотном воздействии следует положить все сто=0).

В полученном ранее автомодельном решении гауссовской формы [19] функция

Дт^у) была задана в виде

х 2°*,о/

Приближенное решение уравнений (1) при начальных условиях (3), в которых ц/то(т) определены (4), будем искать в форме функции такого же вида, но с параметрами, зависящими от т| :

Мп^Мл^-Мл); от(л)]ехр{Ю[т-^т(л); Мп); Мп)]-Рп} •

Их начальные значения определяются параметрами входного воздействия:

Ап^)='^то’ ат^)=лто’ ^т(^)-^то> ст^)“cmo> ^т(^)-^ •^

Объединим входящие в (8) неизвестные функции в блочный вектор

W=Wn)^2(n),~^0°)

где

Хт(л)={МпММп),Мп)>Мп)Мп)^(И)

Для их определения воспользуемся вариационным методом, который базируется на гамильтоновом представлении уравнений динамики [21] и широко используется в теории нелинейных волн [22]. В рассматриваемой здесь задаче аналогично [18, 19] наилучшее (в смысле принципа Гамильтона) приближение автомодельного представления (8) к точному решению уравнений (1) достигается при выборе вектора А(т|), удовлетворяющего вариационным уравнениям

— = 0; А = 1,2,...,6#                           (12)

где х^(т|) - компоненты векторов (11), а фг.^/п)-Ь^Ф.Ф;,®;,^                     (13)

• - лагранжиан с плотностью Л(Ф,Ф\,Ф_Т)), зависящей от вектора функций

Ф(ПД)={ф1(П,т),ф\(Л,т),...,Фм^

и его производных по т и т], ф'т и Ф^.

Здесь

Для уравнений (1) с учетом подстановки (14) плотность лагранжиана, как показано в

[19], представима в виде

N л(ф,ф;,ф„)=£ *=1

-~ IX |<Рт Г |ф/ Г ехр(-2р„11)

2 /-1

+а«

^т дх

Подставляя функцию (14) с учетом (5), (6) и (8) в (15) и выполнив интегрирование согласно (13), получаем а,

dA*w

-dA

Л —

я²₂ db_ dq            2ct 2      - ₂       ,

— ^_ 2 c ^ 2y c + ——+—xa a + 2a c 6 м •     м .      । м м * 2   * мим им

^H ^n          3a* 3

П J

\     /     \

2 X-q.

- secA ----- dx ) \ ^д/ >

После определения вариационных производных выражения (16) по входящим в него неизвестным параметрам, зависящим от и , подставновки их в (12) и несложных преобразований получается следующая система обыкновенных дифференциальных уравнений для указанных параметров модели (8): da

—— = 4аа b  ;

/X

N

-ех^-гР-т^к^Д^^     ;(18)

/=i

N

"^■ = 2exp(-2p_n)^^^a,,a,,,,-,^) ;(19)

dq

~ = 2a-CM +Гж ;      m = 1,2,...,N ;

db

к 2 a. -7-4bl

где

^^A^ th ------- a. V a. )

к = 4Д2 (      \ sech ----- к a. )

2 ^T~9/ secA -----

I a,

При этом

4(п)

Полученная система из 4N нелинейных обыкновенных дифференциальных уравнений (17)-(20) описывает эволюцию параметров импульса секанс-гиперболической формы (5), аппроксимирующего точное решение системы НУШ (1). Сравнивая ее с аналогичной системой, полученной в [19] для гауссовского импульса (7), нетрудно заметить, что они отличаются только коэффициентом к и видом функций в правой части. Для гауссовской модели ^=1, 2 2^2

(   2 )

^т^т^-^гехр ”^Т ^aml V ^Q ml )

\ ^т1 Ч mi        Чт1

Ж-М.ЛЬ -5-^СХР

We a2ml=a2m+a2l 1 ЧтГ<1пГЧ1 •

При использовании секанс-гиперболической модели в правую часть уравнений (18) и (19) входят функции, аналитические выражения которых, если выполнить интегрирование в (22) и (23), оказываются очень громоздкими (и поэтому здесь опущены). При моделировании на ЭВМ их целесообразно определять путем численного интегрирования. В отличие от этого для гауссовской модели аналогичные функции, как видно из (25), имеют сравнительно простой вид, что ускоряет моделирование. Более подробное сравнение указанных двух моделей рассматривается ниже.

Результаты и выводы

Рассмотренный подход к анализу процессов самовоздействия импульсов в нелинейных оптических средах с модовой дисперсией позволяет перейти от их исходной модели в форме системы нелинейных уравнений в частных производных вида (1), т.е. в бесконечномерном пространстве состояний, к приближенному представлению в конечномерном пространстве параметров в виде системы обыкновенных дифференциальных уравнений (17)-(20). Свойства таких систем детально исследованы и известны многочисленные методы их приближенного и численного решения. При моделировании их на ЭВМ затраты времени и требования к объему памяти по крайней мере на порядок меньше по сравнению с исходной системой уравнений (1). Это особенно важно при статистическом моделировании с большим числом испытаний, которое необходимо при оценках вероятностей ошибочного приема цифровых сигналов и других статистических характеристик солитонных систем [20].

Полученные уравнения отражают и физический механизм нелинейного взаимодействия мод: за счет нелинейности развивается самомодуляция импульсов, проявляющаяся в изменениях как коэффициентов ЛЧМ b_m, так и средних частот мод (смещении их на с_ш) в соответствии с(18)и(19),а эти параметры в свою очередь влияют на ширину а_т и взаимное смещение q_m компонент импульса по отдельным модам согласно уравнениям (17) и (20).

Зависимости характера эволюции указанных величин от параметров нелинейности кт1 при использовании секанс-гиперболической аппроксимации аналогичны тем, которые были исследованы ранее для гауссовской модели [19].

При расчетах преобразований импульсных сигналов в нелинейных оптических средах С модовой дисперсией, как правило, необходимо знать параметры суммарного импульса, а не его компонент по отдельным модам (исключение составляют лишь области применения, где используется селекция мод). Наиболее важным из таких параметров является длительность (ширина) импульса, поскольку именно от нее зависят предельно достижимые скорость передачи информации, быстродействие и т.п. характеристики систем и устройств, в которых используются солитонные импульсы.

Поскольку рассматриваемые здесь импульсы не являются финитными, их необходимо характеризовать некоторой эквивалентной шириной (или полушириной). Из различных известных определений последней в данном случае наиболее удобной для расчетов является среднеквадратическая (по интенсивности) полуширина, определяемая как

где

- энергия импульса,

- среднее значение т .

Для одиночного импульса секанс-гиперболической формы (5) среднеквадратическая полуширина по интенсивности т6=аол/2^3 для гауссовского импульса (7) Ts=ao/V2.

Применяя это определение к импульсу |\|/(^,п,т)|² , образованному путем сложения интенсивностей всех мод, каждая из которых описывается выражением вида (8), получаем n     (nV

где тупя гауссовской модели v—0,5 , для секанс-гиперболической v ti²/12.

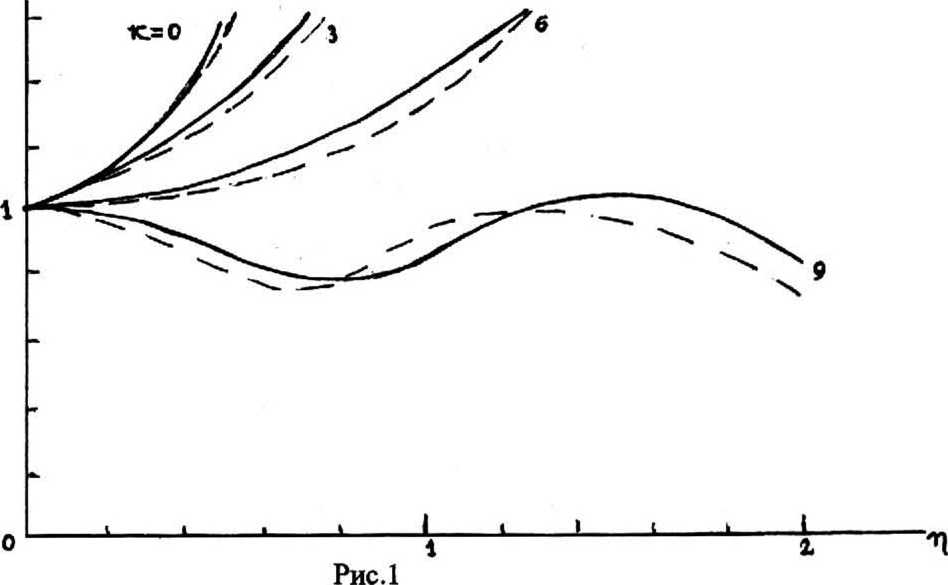
В целях сравнения результатов, полученных на основе рассмотренных параметрических моделей и прямого решения исходных НУШ (1), было проведено моделирование на ЭВМ. Уравнения (17)-(20) решались численно методом Рунге-Кутта четвертого порядка, а система уравнений (1) - методом расщепления по физическим факторам с применением быстрого преобразования Фурье. Результаты моделирования показывают, что форма модовых компонент импульса в режимах, близких к солитонному, при использовании секанс-гиперболического приближения несколько лучше соответствует точному решению, чем при гауссовской модели. Для суммарного импульса указанное различие меньше.

На рис.1 показаны графики эволюции среднеквадратической полуширины т5(т|), определяемой по формуле (27), для импульса, распространяющегося в двухмодовом световоде, полученные на основе секанс-гиперболической (сплошные линии) и гауссовской (штриховые линии) моделей при различных значениях параметра нелинейности к . В этом примере все к^ = к , а остальные параметры имели следующие значения:

Ло"¹⁷^; “„^ Г1=-Г₂=²’ ^Ьт0 = ^Ст0 = ^0 = ⁰ S ^ = ² V3 / Л ; для гауссовского импульса а_то=^.

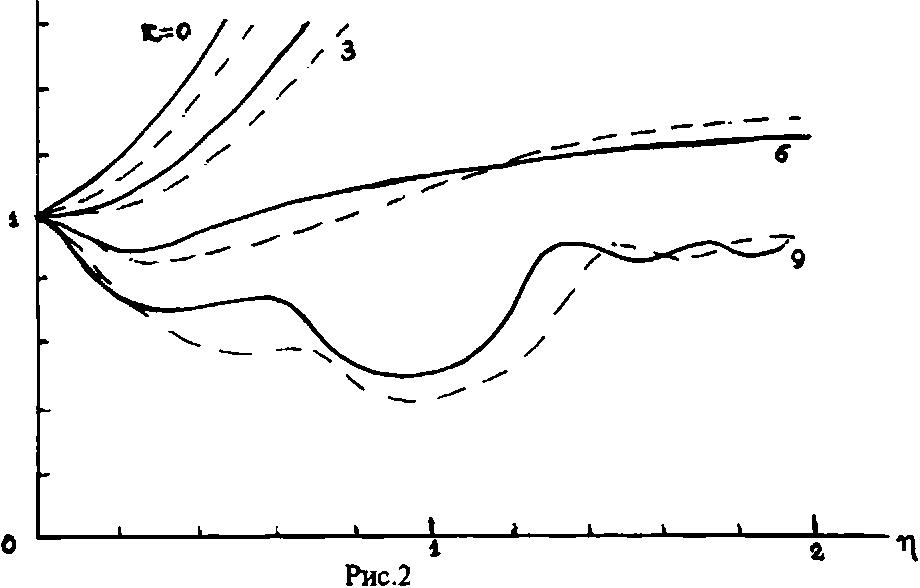
Как видно из этих зависимостей, ширина импульса вследствие дисперсионных эффектов (материальной, волноводной и модовой дисперсии) в линейном режиме (к=0) быстро возрастает вдоль волокна. С увеличением мощности импульса и, соответственно, параметра к , это дисперсионное расширение замедляется благодаря нелинейным эффектам: частота и групповая задержка каждой модовой компоненты импульса в соответствии с уравнениями (17)-(20) изменяются за счет интенсивности второй моды (в общем случае - нескольких других мод) так, что волновой пакет начинает сжиматься, а дисперсия его - компенсироваться. Значение параметра к соответствующее самостабилизации импульса за счет полной компенсации дисперсии (т.е. образованию солитона) в этом примере равно приблизительно 8. При к > 8 действие нелинейных эффектов еще сильнее и вызывает сжатие импульса, так что его общая ширина осциллирует в результате конкуренции нелинейных и дисперсионных эффектов.

Сравнение сплошных и штриховых кривых показывает, что различия в эволюции секанс-гиперболических и гауссовских импульсов с одинаковой начальной среднеквадратической полушириной незначительны. Таким образом, при прочих равных условиях гауссовское приближение может оказаться предпочтительным, как более простое. Разумеется, главным фактором, который следует принимать во внимание при выборе модели, является реальная форма входного импульса.

Аналогичные графики эволюции полуширины суммарного импульса двух мод, полученные при тех же значениях всех параметров путем прямого численного решения уравнений (1) указанным выше методом, представлены на рис.2. Сравнение их с рис.1 обнаруживает их достаточно хорошее соответствие.

В целом полученные результаты показывают: в тех случаях, когда детали эволюции формы импульсов (такие, как появление боковых лепестков, "пьедесталов", деформация вершины и т.п.) не существенны для работы исследуемых оптических систем и устройств, при их расчетах с успехом могут быть использованы рассмотренные параметрические модели.