Приближенный метод расчета нестационарного температурного поля в полом цилиндре

Задачи, связанные с определением нестационарного температурного поля в стенках цилиндрической формы, часто встречаются в инженерной практике. Как правило, аналитические решения таких задач содержат различные типы Бесселевых функций ( Лыков , 1967), что в значительной степени их усложняет и, следовательно, затрудняет выполнение числовых расчетов. Предлагаемый приближенный аналитический метод расчета нестационарного температурного поля позволяет отказаться от использования функций Бесселя и получить результаты высокой точности.

2. Расчет нестационарного температурного поля в полом цилиндре

Рассмотрим предлагаемый приближённый метод расчета переноса тепла в цилиндрических

стенках на примере следующей задачи:

а т    [ d 2т i d т ) ---= a l т +--1 ,                                                    (1) д т   ^ дТ 2 Т дт J T = T 1 , при r = R 1 ,                                          (2) T = T 2 , при r = R 2 ,                                          (3) T = T 0 , при τ = 0.                                           (4)

Строгое аналитическое решение системы (1-4) приведено в монографии ( Лыков , 1967). Однако оно является сравнительно сложным и громоздким, поэтому использовать его в инженерных расчетах затруднительно.

Приведем задачу (1-4) к безразмерному виду д т _ d 2 ^   1 dS

д Fo "ду ^{2 +} у ду ’ S = 1 , при V = 1 , S = S = т 2 / t_v при у = у * = R 2 /R₁ ,

S = S ₀ = Т 0 / T_v при Fo = 0 , где S = T / Т 1 ; у = r / R 1 ;Fo = а т / R 1² .

Представим искомое температурное поле S ( у, Fo) в виде суммы двух решений

S ( v ,Fo ) = ^у ) + U ( y ,Fo ) ,                        (9)

где

^ ( у ) = 1 + ( s‘ - 1 ) ln y /ln y ‘,                               (10)

Вестник МГТУ, том 16, №1, 2013 г.   стр.40-42

стационарное распределение температуры в цилиндрической стенке, т.е. когда число Fo стремится к бесконечности ( Fo => ∞), U( ψ , Fo ) – нестационарная составляющая температурного поля. Эта функция должна удовлетворять следующей системе уравнений:

	д и  д 2 и  1 д и =    ,+        ,                                      (11) д Fo   ду 2   у ду U = 0 , при у = 1 ,                                 (12) U = 0 , при у = у *,                               (13) U = / ( у ) , при Fo = 0 ,                           (14)
где	F ( у ) = ^ _ ^ ( у ) .                               (15)

Переменный коэффициент 1/ ψ в правой части дифференциального уравнения (11) очевидно

меняется в пределах

b min = 1/ у * ^ 1/ у ^ b max = 1.                              (16)

Если в (11) заменить переменный коэффициент 1/ψ на некоторый постоянный b, расположенный в интервале (16), то допустимо приближенно аппроксимировать зависимость (11) уравнением вида д U   д2 U , д U

----=----+ b---, д Fo ду ду тогда интервал задачи (17), (12-14) можно выразить соотношением _ b и (у, Fo ) = E2 yW (у, Fo), где функция W(ψ,Fo) находится путем интегрирования системы уравнений где

д W   д ²W  b²_TT7

— =—--- w , д Fo   ду ²    4

W = 0, при ψ = 1,

W = 0, при ψ = ψ *,

W = W ( ψ ), при Fo = 0,

W ( у ) = / ( у > "^у

Используя метод разделения переменных ( Видин, Иванов , 2012), аналитическое решение искомой зависимости можно представить в виде бесконечной суммы

У^  f w (¥^0 ) = ^ А« sm п=1   V '       „-• Е - Brу -1)«_ '-Fo                    (24) -                         ^           V, где формула (24) удовлетворяет дифференциальному уравнению (19), граничному условию (20) и условию на поверхности ψ = ψ* (21), если собственные числа µn рассчитываются по простой зависимости

Ц п = V ( п п / ( у* _ 1 )) ² + В ²/4 .

Коэффициенты ряда (24) находятся из начального условия задачи, т.е.

тс

Z А

П = 1

sin

V

и

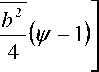
sin

Собственные функции данного решения

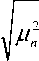
= W ( у ) .

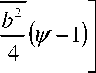
обладают свойством

ортогональности, т.е.

*

V

J „„

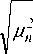
b² 4

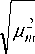
b² 4

d V = 0 , при п Ф m ,

*

V

J sin

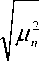
b ²

поэтому коэффициенты ряда An будут равны

A

*

V

J ^w ( V ) sin

*

V

J ^sin2

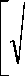
m N

sin sin

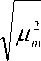
b ²

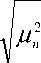
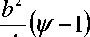
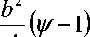
d V ^ 0 , при n = m ,

d y

d y

Причем знаменатель в формуле (29) находится по выражению ( Бронштейн, Семендяев , 1965):

V

J ^sin2

mN

B- ( v - 1 ^{) d V} = 2 ^

*

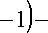
sin 2

M

-

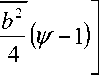
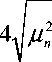
- b2

Таблица. Собственные числа µ n

ψ *	µ 1		µ 2		µ 3
	Расчет по методике *	Расчет по формуле (25)	Расчет по методике *	Расчет по формуле (25)	Расчет по методике *	Расчет по формуле (25)
1,2	15,7014	15,7067	31,4126	31,4033	47,1217	47,1022
1,5	6,2702	6,2938	12,5598	12,5669	18,8451	12,5669
2	3,1230	3,1623	6,2734	6,2912	9,4182	9,4275

* - Лыков, 1967.

Таким образом, полученное приближенное решение исходной задачи не содержит специальных функций Бесселя и включает в себя хорошо известные элементарные функции.

3. Заключение

Предложенный приближенный аналитический метод расчета нестационарного температурного поля полого цилиндра позволяет вести расчеты, не используя специальные функции Бесселя. Результаты решения поставленной задачи удовлетворяют предъявляемым требованиям по точности решения и обладают меньшей сложностью по сравнению с классическими методами решения.