Приближенный метод расчета распределения температуры в комбинированном радиальном ребре прямоугольного профиля

Известно, что развитые поверхности теплообмена широко применяются в самых различных отраслях техники. Постоянное совершенствование таких типов поверхностей способствует созданию более компактных и эффективных конструкций теплопередающих аппаратов. Одновременно необходимо развивать математические методы инженерного расчета процессов теплопереноса в ребристых элементах подобных систем.

В статье на примере комбинированного радиального ребра прямоугольного сечения рассмотрен приближенный способ определения стационарного температурного поля в неоднородном теле.

2. Результаты исследований

Исследуемый процесс теплопроводности в составном радиальном ребре может быть описан

следующей системой уравнений:

d 2 ϑ    1 d ϑ 1    + ⋅ 1 - m 1 2 ϑ 1 = 0 ,                                                       (1) dr 2    r dr r 0 ≤ r ≤ r 1 ; d 2 ϑ    1 d ϑ 2    + ⋅   2 - m 2 2 ϑ 2 = 0 ,                                                   (2) dr 2     r dr r 1 ≤ r ≤ r 2 ; ϑ 1 = ϑ 0 = t 0 – t Г при r = r 0 ;                                         (3) ϑ 1 = ϑ 2 при r = r 1 ;                                           (4) d ϑ   λ d ϑ 1    = 2 ⋅ 2 при r = r 1 ;                                                  (5) dr    λ 1 dr d ϑ 1 = 0 при r = r .                                                  (6) dr

Здесь u 1 = t 1 – t Г ; u 2 = t 2 – t Г – избыточная температура стержня на начальном участке ( r 0 ≤ r ≤ r 1 ) и конечном ( r ₁ ≤ r ≤ r ₂) соответственно; m ₁ = ( α / λ ₁ δ )^0,5, 1/м; m ₂ = ( α / λ ₂ δ )^0,5, 1/м – параметры для первого и второго участков соответственно; α – коэффициент теплоотдачи, Вт/м²∙К; λ ₁, λ ₂, Вт/м∙К – коэффициенты теплопроводности материалов ребра на начальном и конечном участках соответственно; t 0 , t Г – температура основания ребра и окружающей среды соответственно.

Видин Ю.В., Казаков Р.В. Приближенный метод расчета распределения…

Условие (4) справедливо, если термический контакт между разнородными частями ребра является идеальным.

Общее аналитическое решение уравнений (1) и (2) определяется соотношениями ( Керн, Краус , 1977)

V1(r) = C110 (m 1 r) + C2K0 (m 1 r); ^2(r) = C310 (m2r) + C4K0 (m2r), где I0(x) и K0(x) – модифицированные функции Бесселя первого и второго рода нулевого порядка (Видин и др., 2007).

Произвольные постоянные C 1 , C 2 , C 3 , C 4 определяются с помощью граничных условий (3-6). После подстановки зависимостей (7) и (8) в формулы (3-6) удается составить систему из четырех алгебраических уравнений, решая которую находятся указанные коэффициенты.

Однако выражения для их вычисления получаются сравнительно сложными и содержат большое количество параметров. В результате этого расчеты оказываются громоздкими и трудоемкими. Поэтому целесообразно разработать более простой метод исследования температурных полей A и А ₂ .

Так как первая часть ребра по условию задачи выполнена из высокотеплопроводного материала (например, медь, алюминий или сплавы на их основе), то имеет место сильное неравенство Л ₁» Л ₂, отсюда

dA dA

>> —² dr

.

следует, что    1

dr

Тогда допустимо приближенно принять, что на стыке между разными участками ребра

и

dA dr

= 0.

•= r

Благодаря такому упрощению исходную задачу можно разделить на две отдельные самостоятельные, а именно

d 2V i d V   2, --г + — -г1 - m fVi = 0 ; dr 2     r dr	(10)
r 0 < r < r 1 ;
^ 1 = A ) = 1 0 - t r при r = r 0 ;	(11)
d V „ —L = 0 при r = r i dr	(12)
d 2V2   i d V2    2. n —+-•    - m 2 2V 2 = 0 ; dr 2     r dr	(13)
r 1 < r < r 2 ;
A 2 = A 1 при r = r 1;	(14)
d V2 A —2 = 0 при r = r 2. dr	(15)

Математическое решение первой системы (10-12) как известно, имеет вид ( Керн, Краус , 1977)

0 _ 0    ^K i⁽ m i r i ) I 0⁽ m i ^r ) ⁺ 1 i⁽ m i r i ) K 0⁽ m i ^r )

V i = V 0------------------------------------- ,

I 0⁽ m i r o ) K i⁽ m i r i ) ⁺ I i⁽ m i r i ) K 0^{( m} i r o )

где I ₁( x ), K ₁( x ) – модифицированные функции Бесселя первого и второго рода первого порядка ( Видин и др. , 2007).

Отсюда избыточная температура на конце первой части ребра будет равна

_V ( r = r ) = _V K i⁽ m i r i ) I 0⁽ m i r i ) ⁺ I i⁽ m i r i ) K 0⁽ m i r i ) ^{i i 0} 1 0 ( m i r b ) K i ( m i r i ) + 1 i ( m i r i ) K 0 < m i Г 0 ) '

Учитывая, что существует равенство (Градштейн, Рыжик, 1963) I0(x) K1(x) + I1(x) K0(x) = 1/x, выражение (17) примет вид

A ( r = r 1 ) = — [ 1 0 ( m 1 r 0 ) K 1 ( m 1 r 1 ) + 1 1 ( m 1 r 1 ) K q ( m 1 r 0 )] " ¹.

m i r i

После подстановки (18) в граничное условие (14), получим зависимость для расчета температуры на периферийной части ребра

Вестник МГТУ, том 14, №3, 2011 г.   стр.511-514

ϑ 2 =

— [ I o ( m 1 r 0 ) K 1 ( m 1 r 1 ) + 1 1 ( m 1 r 1 ) K ₀ ( m 1 r o )] ^{- 1} m i r i

^K i^{( m} 2 ^r 2 ) I 0^{( m} 2 ^r ) ⁺ 1 1 ( ^m 2 ^r 2 ) K 0^{( m} 2 ^r )

I o⁽ m 2 r i )K i⁽ m 2 r 2 ) + I i⁽ m 2 ^r 2 ) K o^{( m} 2 ^r1 ) '

Решения (16) и (19) полностью удовлетворяют уравнениям (1-4) и (6) исходной задачи. Они не являются достаточными только для условия (5).

Однако при их подстановке в формулу (5) возникающая невязка, как правило, оказывается весьма незначительной. Это обстоятельство особенно является заметным при сравнительно малой величине отрезка ( r ₁- r ₀).

Применительно к инженерным расчетам к достоинствам приближенных формул (16) и (19) следует отнести их математическую простоту и малую погрешность.

Из-за принятого выше допущения (9) следует, что расчеты по зависимостям (16) и (19) приводят к несколько завышенным значениям избыточной температуры по сравнению с фактическими.

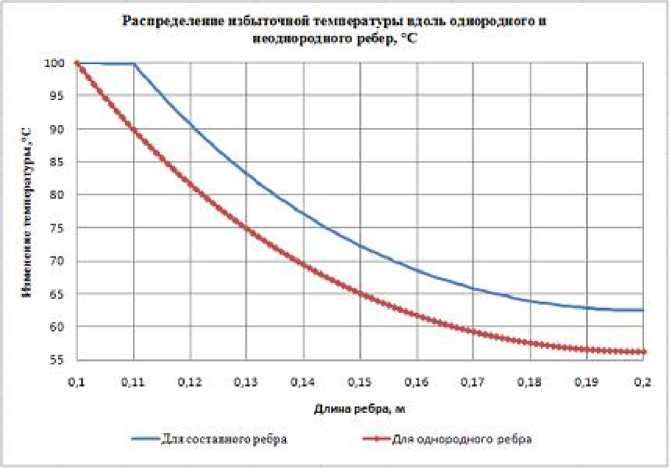
Рис. Распределение избыточной температуры вдоль однородного и неоднородного радиальных ребер

На рисунке изображены кривые изменения температуры по радиальному ребру, рассчитанные по (16) и (19), для случая r ₀ = 50 мм, r ₁ = 60 мм, r ₂ = 100 мм, δ = 4 мм, λ ₁ = 237 Вт/м∙К, λ ₂ = 45 Вт/м∙К, α = 20 Вт/м²∙К, t ₀ = 120 °C, t_Г = 20 °C. Здесь же приведена кривая изменения температуры по радиусу такого же ребра, выполненного из однородного материала, у которого λ = 45 Вт/м∙К. Из сопоставления полученных результатов видно, что даже при сравнительно малой начальной части, обладающей более высокой теплопроводностью, существенно возрастает температурный напор по длине ребра. Кроме этого, в таблице к рисунку приведены дополнительные числовые значения температурного напора в зависимости от радиуса рассматриваемого сечения.

• 3.    Выводы

• 1)    Предложена конструкция радиального ребра, у которого начальная часть выполнена из материала, обладающего более высоким коэффициентом теплопроводности, чем периферийная.

• 2)    Применение комбинированных ребер предлагаемого типа позволяет существенно повысить по их длине температурный напор и благодаря этому увеличить коэффициент тепловой эффективности таких поверхностей.

• 3)    Разработан эффективный приближенный аналитический метод расчета изменения температуры в радиальном направлении составных ребер, обладающих достаточной для инженерной практики точностью.

• 4)    Рекомендуемый метод может быть использован для расчета распространения тепла в развитых комбинированных поверхностях при любой конфигурации ребер.

Видин Ю.В., Казаков Р.В. Приближенный метод расчета распределения…

Таблица. Численные показатели величины избыточной температуры однородного и неоднородного радиальных ребер в зависимости от радиуса

Длина ребра, м	Величина избыточной температуры неоднородного радиального ребра, °С	Величина избыточной температуры однородного радиального ребра, °С
0,10	100,000	100,000
0,11	99,891	89,876
0,12	90,682	81,591
0,13	83,180	74,840
0,14	77,124	69,392
0,15	72,316	65,065
0,16	68,596	61,718
0,17	65,842	59,240
0,18	63,957	57,544
0,19	62,866	56,563
0,20	62,512	56,245